Что такое двоичные разряды
Двоичная система счисления
Чисто технически было бы очень сложно сделать компьютер, который бы «понимал» десятичные числа. А вот сделать компьютер, который понимает двоичные числа достаточно легко. Двоичное число оперирует только двумя цифрами – 0 и 1. Несложно сопоставить с этими цифрами два состояния – вЫключено и включено (или нет напряжения – есть напряжение). Процессор – это микросхема с множеством выводов. Если принять, что отсутствие напряжения на выводе – это 0 (ноль), а наличие напряжения на выводе – это 1 (единица), то каждый вывод может работать с одной двоичной цифрой. Сейчас мы говорим о процессоре очень упрощённо, потому что мы изучаем не процессоры, а системы исчисления. Об устройстве процессора вы можете почитать здесь: Структура процессора.
Конечно, это касается не только процессоров, но и других составляющих компьютера, например, шины данных или шины адреса. И когда мы говорим, например, о разрядности шины данных, мы имеем ввиду количество выводов на шине данных, по которым передаются данные, то есть о количестве двоичных цифр в числе, которое может быть передано по шине данных за один раз. Но о разрядности чуть позже.
Итак, процессор (и компьютер в целом) использует двоичную систему, которая оперирует всего двумя цифрами: 0 и 1. И поэтому основание двоичной системы равно 2. Аналогично, основание десятичной системы равно 10, так как там используются 10 цифр.
Каждая цифра в двоичном числе называется бит (или разряд). Четыре бита – это полубайт (или тетрада), 8 бит – байт, 16 бит – слово, 32 бита – двойное слово. Запомните эти термины, потому что в программировании они используются очень часто. Возможно, вам уже приходилось слышать фразы типа слово данных или байт данных. Теперь, я надеюсь, вы понимаете, что это такое.
Отсчёт битов в числе начинается с нуля и справа. То есть в двоичном числе самый младший бит (нулевой бит) является крайним справа. Слева находится старший бит. Например, в слове старший бит – это 15-й бит, а в байте – 7-й. В конец двоичного числа принято добавлять букву b. Таким образом вы (и ассемблер) будете знать, что это двоичное число. Например, А теперь попробуем понять, как формируется двоичное число.
Ноль, он и в Африке ноль. Здесь вопросов нет. Но что дальше. А дальше разряды двоичного числа заполняются по мере увеличения этого числа. Для примера рассмотрим тетраду. Тетрада (или полубайт) имеет 4 бита.
| Двоичное | Десятичное | Пояснения |
| 0000 | 0 | — |
| 0001 | 1 | В младший бит устанавливается 1. |
| 0010 | 2 | В следующий бит (бит 1) устанавливается 1, предыдущий бит (бит 0) очищается. |
| 0011 | 3 | В младший бит устанавливается 1. |
| 0100 | 4 | В следующий бит (бит 2) устанавливается 1, младшие биты (бит 0 и 1) очищаются. |
| 0101 | 5 | В младший бит устанавливается 1. |
| 0110 | 6 | Продолжаем в том же духе. |
| 0111 | 7 | . |
| 1000 | 8 | . |
| 1001 | 9 | . |
| 1010 | 10 | . |
| 1011 | 11 | . |
| 1100 | 12 | . |
| 1101 | 13 | . |
| 1110 | 14 | . |
| 1111 | 15 | . |
Итак, мы видим, что при формировании двоичных чисел разряды числа заполняются нулями и единицами в определённой последовательности:
Если младший равен нулю, то мы записываем туда единицу. Если в младшем бите единица, то мы переносим её в старший бит, а младший бит очищаем. Тот же принцип действует и в десятичной системе: Всего для тетрады у нас получилось 16 комбинаций. То есть в тетраду можно записать 16 чисел от 0 до 15. Байт – это уже 256 комбинаций и числа от 0 до 255. Ну и так далее. На рис. 2.2 показано наглядно представление двоичного числа (двойное слово).
Старшие и младшие разряды чисел
Чисто технически было бы очень сложно сделать компьютер, который бы «понимал» десятичные числа. А вот сделать компьютер, который понимает двоичные числа достаточно легко. Двоичное число оперирует только двумя цифрами – 0 и 1. Несложно сопоставить с этими цифрами два состояния – вЫключено и включено (или нет напряжения – есть напряжение). Процессор – это микросхема с множеством выводов. Если принять, что отсутствие напряжения на выводе – это 0 (ноль), а наличие напряжения на выводе – это 1 (единица), то каждый вывод может работать с одной двоичной цифрой. Сейчас мы говорим о процессоре очень упрощённо, потому что мы изучаем не процессоры, а системы исчисления. Об устройстве процессора вы можете почитать здесь: Структура процессора.
Конечно, это касается не только процессоров, но и других составляющих компьютера, например, шины данных или шины адреса. И когда мы говорим, например, о разрядности шины данных, мы имеем ввиду количество выводов на шине данных, по которым передаются данные, то есть о количестве двоичных цифр в числе, которое может быть передано по шине данных за один раз. Но о разрядности чуть позже.
Итак, процессор (и компьютер в целом) использует двоичную систему, которая оперирует всего двумя цифрами: 0 и 1. И поэтому основание двоичной системы равно 2. Аналогично, основание десятичной системы равно 10, так как там используются 10 цифр.
Каждая цифра в двоичном числе называется бит (или разряд). Четыре бита – это полубайт (или тетрада), 8 бит – байт, 16 бит – слово, 32 бита – двойное слово. Запомните эти термины, потому что в программировании они используются очень часто. Возможно, вам уже приходилось слышать фразы типа слово данных или байт данных. Теперь, я надеюсь, вы понимаете, что это такое.
Отсчёт битов в числе начинается с нуля и справа. То есть в двоичном числе самый младший бит (нулевой бит) является крайним справа. Слева находится старший бит. Например, в слове старший бит – это 15-й бит, а в байте – 7-й. В конец двоичного числа принято добавлять букву b. Таким образом вы (и ассемблер) будете знать, что это двоичное число. Например, А теперь попробуем понять, как формируется двоичное число.
Ноль, он и в Африке ноль. Здесь вопросов нет. Но что дальше. А дальше разряды двоичного числа заполняются по мере увеличения этого числа. Для примера рассмотрим тетраду. Тетрада (или полубайт) имеет 4 бита.
| Двоичное | Десятичное | Пояснения |
| 0000 | – | |
| 0001 | 1 | В младший бит устанавливается 1. |
| 0010 | 2 | В следующий бит (бит 1) устанавливается 1, предыдущий бит (бит 0) очищается. |
| 0011 | 3 | В младший бит устанавливается 1. |
| 0100 | 4 | В следующий бит (бит 2) устанавливается 1, младшие биты (бит 0 и 1) очищаются. |
| 0101 | 5 | В младший бит устанавливается 1. |
| 0110 | 6 | Продолжаем в том же духе. |
| 0111 | 7 | . |
| 1000 | 8 | . |
| 1001 | 9 | . |
| 1010 | 10 | . |
| 1011 | 11 | . |
| 1100 | 12 | . |
| 1101 | 13 | . |
| 1110 | 14 | . |
| 1111 | 15 | . |
Итак, мы видим, что при формировании двоичных чисел разряды числа заполняются нулями и единицами в определённой последовательности:
Если младший равен нулю, то мы записываем туда единицу. Если в младшем бите единица, то мы переносим её в старший бит, а младший бит очищаем. Тот же принцип действует и в десятичной системе: Всего для тетрады у нас получилось 16 комбинаций. То есть в тетраду можно записать 16 чисел от 0 до 15. Байт – это уже 256 комбинаций и числа от 0 до 255. Ну и так далее. На рис. 2.2 показано наглядно представление двоичного числа (двойное слово).
Мы поможем найти Вам клиентов!
Самый младший двоичный разряд и самый старший двоичный разряд
Нужны новые клиенты? Тогда Вам рекомендуем посмотреть этот раздел нашего сайта
_____
Самый младший двоичный разряд и самый старший двоичный разряд
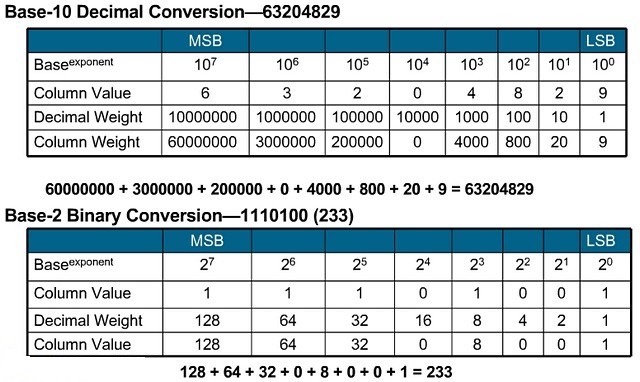
Системой счисления, которую привыкли использовать большинство людей, является десятичной системой. Мы используем десять цифр 0-1-2-3-4-5-6-7-8-9, и увеличиваем значение степени 10. Возможно, первые люди считали на пальцах; иначе мы могли бы использовать и систему счисления с основанием 6 или 17. Таким образом, основание числа очень важно в любой системе счисления, это положения цифры, которое соответствует степени основания. Когда мы считаем от 0 до 10, мы получаем 1 в позиции десяток и 0 ноль в позиции единиц. Продолжая считать до 100, размешаем 1 в позицию сотен, и 0 в позиции десятков и единиц. Это то, что называется позиционной системой счисления.
В двоичном числе, самая правая цифра представляет собой самый младший двоичный разряд (least significant bit (LSB)), а самая левая цифра – самый старший двоичный разряд (most significant bit (MSB)). Значение разряда любой цифры между этими двумя, младшим и старшим, разрядами, зависит от положения между LSB и MSB.
СИСТЕМА СЧИСЛЕНИЯ С ОСНОВАНИЕМ 2
Знание системы счисления с основанием 2 важно, потому что протокол IP version 4 (IPv4) использует адреса, состоящие из 32 битов. 32 бита разделены на 4 группы по 8 бит, называемых октетами. Для разделения их используется точка, расположенная между октетами. (Другое название для 8 бит это байт, но в этом модуле будет использоваться название октет).
Разряд (позиция, место) — это структурный элемент представления чисел в позиционных системах счисления.
Разряд является «рабочим местом» цифры в числе. Порядковому номеру разряда соответствует его вес — множитель, на который надо умножить значение разряда в данной системе счисления.
Диапазон значений для всех разрядов (в данной системе счисления) неизменен.
Содержание
Определение [ править | править код ]
соответствует представлению z в виде суммы
Пример [ править | править код ]
то есть, цифра в нулевом разряде (справа, начиная с нуля) умножается на 10 в нулевой степени. Цифра в первом разряде — на 10 в первой степени, и т. д.
Первые разряды [ править | править код ]
единицы – от 0 до 9, десятки – от 10 до 99, сотни – от 100 до 999, тысячи – от 1000 до 9999, десятки тысяч – от 10000 до 99999, сотни тысяч – от 100000 до 999999, миллионы – от 1 000 000, миллиарды – от 1 000 000 000,
триллионы – от 1 000 000 000 000, далее идут – квадриллион, квинтиллион, секстиллион, септиллион, октиллион и т. д.
Двоичная система для чайников
Я решил сделать серию постов по информатике для чайников.
Если первый пост пойдёт хорошо, то будет еще несколько в том же духе.
Чтобы провести хирургическую операцию, анатомию знать не обязательно, но вот результаты будут непредсказуемы. Точно так же, чтобы программировать, не обязательно знать, как компьютер устроен изнутри, но иногда такое незнание может привести к душераздирающим последствиям.
Основа основ современного компьютера – ДВОИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ (2-СС). Звучит угрожающе. Чтобы понять, что такое ДСС, и научиться с ней работать, надо уметь складывать, умножать и возводить числа в степень. Ок, даю шпаргалку.
Пусть у нас есть какое-то число. Допустим, 5. И мы хотим прибавить к нему другое число. Допустим, 3. Как нам это сделать? Давайте, представим число 5 как пять палочек:
А число 3 как три палочки:
Чтобы сложить их, сначала нарисуем пять палочек, потом допишем к ним еще три:
Теперь пересчитаем – получилось 8.
Зря смеётесь! Когда считаем палочками – в Википедии это называется (ВНИМАНИЕ! НЕНОРМОТИВНАЯ ЛЕКСИКА!) «Единичная непозиционная система счисления с единичным весовым коэффициентом». Ну, или попросту будем называть УНАРНАЯ СИСТЕМА СЧИСЛЕНИЯ (1-СС).
В обычной жизни мы (люди) пользуемся ДЕСЯТЕРИЧНОЙ СИСТЕМОЙ СЧИСЛЕНИЯ (10-СС). Она так называется, потому что у нас есть десять цифр. К тому же, она еще и ПОЗИЦИОННАЯ, что означает, что значение (вес) цифры зависит от её положения в записи числа, например, в числах 2, 21 и 211 цифра 2 означает, соответственно, единицы, десятки и сотни.
Десятичная система счисления
Как мы складываем в 10-СС? Например, столбиком:
Сначала складываем единицы: 2+9 = 11, т.е. при сложении двух единичных чиселок появился новый десяток. Ясное дело, что из них может появиться только один десяток, потому что самое большое, что можно сложить – это 9+9 = 18. Таким образом, разбиваем сложение на кусочки: вместо 12+99 мы делаем 2+9 + 10+90, т.е. единицы и десятки (а потом и сотни) складываем отдельно друг от друга:
12 + 99 = [разобьем на разряды]
= (2+9) + (10+90) = [сложим первые разряды]
= 11 + (10+90) = [снова разобьем на десятки и единицы]
= (1 + 10) + (10 + 90) = [снова перегруппируем, чтобы отделить десятки от единиц]
= 1 + (10 + 10 + 90) = [сложим десятки]
= 1 + (110) = [разобьем на сотни и десятки]
Ясно, что получится 111, но давайте остановимся и посмотрим на эту полученную форму записи:
Фишка в том, что любое число можно представить как сумму отдельно единиц, отдельно десятков, сотен и т.д., например:
564 = 500 + 60 + 4, 7031 = 7000 + 000 + 30 + 1
Особенность такой записи в том, что мы видим во всех разрядах одну значащую цифру (первую), все следующие за ней цифры – это нули. Запомните этот момент – это важно.
При этом вместо того, чтобы писать 1000, мы можем написать 10^3 (т.е. десять в третьей степени, что можно расшифровать как 10*10*10).
7000 = 7*1000 = 7 * 10^3
А всё число 7031 можно расписать так:
7031 = 7*10^3 + 0*10^2 + 3*10^1 + 1*10^0
Напомню, что любое число в нулевой степени даёт единицу, и 10^0 = 1, а любое число в первой степени даёт само себя 10^1 = 10. Еще напомню, что любое число умноженное на 0 даёт 0, т.е. 0*10^2 = 0.
Так вот, наша система счисления называется десятичной именно благодаря этой десятке, которую в степень возводим.
Краткое отступление. Дорогие мои! Не путайте числа и цифры! Путать цифры и числа – это как путать буквы и звуки. Цифра – это просто символ для записи чисел. А число – это абстрактная величина, обычно означающее количество чего-нибудь. Думаю, все поняли. 🙂
Двоичная система счисления
Теперь, поговорим о 2-СС. Её особенность в том, что в ней есть всего 2 символа для записи чисел: 0 и 1. Что интересно, при этом любое число, которое можно записать в 10-СС, так же можно записать и в 2-СС, и даже в 1-СС!
Двоичная система тоже позиционная и отличается от десятичной тем, что в ней вместо 10 в степень возводится двойка, например, число двоичное число 101101 можно прочитать так:
101101= 1*2^5 + 0*2^4 + 1*2^3 + 1*2^2 + 0*2^1 + 1*2^0
= 32 + 0 + 8 + 4 + 0 + 1 = 45 (это уже в десятичной системе)
Теперь давайте поскладываем в двоичной системе.
Начнём с простого: 0+0 = 0, 1+0 = 1, 0+1 = 1
Ничего удивительного, в 10-СС это точно так же выглядит.
Теперь посложнее: 1 + 1 = 10
А вот никакие не ДЕСЯТЬ! Это число ДВА. Просто в двоичной записи.
Нет. Это не десять плюс один! Это два плюс один! В 10-СС это выглядит так: 2 + 1 = 3, а в 1-СС так: || + | = |||. Ясно –понятно?
Хм… сложновато? Давайте упростим! По той же схеме, что и 12 + 99. Не забываем, что всё это в двоичной системе!
11 + 1 = [разобьем на разряды]
= (10 + 1) + 1 = [перегруппируем]
= 10 + (1 + 1) = [О! “1+1” складывать умеем!]
= 10 + 10 = [ну, здесь просто сначала игнорируем нули, складываем 1+1 и потом приписываем 0 к результату]
Ну, сколько можно. Это не СТО. Если то же самое записать в 10-СС, то получим: 3 + 1 = 4. Т.е. это 100 в записи 2-СС – это ЧЕТЫРЕ.
Ну, и для закрепления материала сложим в 2-СС:
= (1000 + 100 + 00 + 1) + (1000 + 000 + 00 + 1)
= (1000 + 1000) + (100 + 000) + (00 + 00) + (1 + 1)
= (10000) + (100) + (00) + (10)
= (10000) + (100) + (00 + 10)
А по-русски: 13 + 9 = 22
Большое спасибо! Очень хорошо объяснили. Всё понял.
А вот никакие не ДЕСЯТЬ! Это число ДВА. Просто в двоичной записи. И дальше нет объяснения почему и как. Естественно дальше идут примеры сложнее, но т.к. этот простой непонятен. Дальше залазить в дебри
поделитесь, пожалуйста, еще постами по информатике если есть
А теперь слушайте домашнее задание: построить синхрофазотрон.
Теперь посложнее: 1 + 1 = 10
Ой! Почему десять.
А вот никакие не ДЕСЯТЬ! Это число ДВА. Просто в двоичной записи.
Я тебя разочарую, но это десять и есть.
Кстати цифровая схемотехника основана на двоичной системе счисления. На основных законах булевой алгебры. 1+1=1 1+0=1 1*1=1 1*1=0
На самом деле все еще проще.
Нейронные сети. Формулы обратного распространения
Представляем заключительную лекцию из курса по нейронным сетям от 3blue1brown. В этой лекции речь пойдет о формулах обратного распространения. Одной из важных тем, которая позволит разобраться с основными моментами дифференцирования сложных функций в контексте сетей.
Благодарим за создание выпуска:
Переводчика – Федора Труфанова;
Редактора – Михаила Коротеева;
Диктора – Никифора Стасова;
Монтажера – Олега Жданова
Нейронные сети. Обратное распространение ошибки
Привет, Лига образования!
Мы продолжаем переводить легендарный курс по нейросетям от 3blue1brown.
В предыдущей лекции мы узнали о градиентном спуске. Сегодня речь пойдет о методе обратного распространения — главном алгоритме обучения нейронных сетей.
Благодарим за создание выпуска:
Редактора – Михаила Коротеева;
Диктора – Никифора Стасова;
Монтажера – Олега Жданова
И бонус в комментариях, английский!
Нейронные сети. Градиентный спуск: как учатся нейронные сети
Обучение — сложный процесс не только для человека, но и для сущностей, порожденных разумом человека.
Мы подготовили долгожданное продолжение лекций по нейросетям. Градиентный спуск: как учатся нейронные сети.
Благодарим за участие в выпуске:
Редакторов – Дмитрия Титова, Михаила Коротеева, Дмитрия Мирошниченко;
Корректора – Дмитрия Мирошниченко;
Дикторов – Никифора Стасова, Дарью Яговкину;
Монтажера – Олега Жданова.
Разговор о системах счисления:
— Программист подарил своей женщине 5 роз, сказав «эта 101 роза тебе» (двоичная). Пещерный человек, подарил бы три розы, сказав «бери эти 111 роз» (унарная).
— То есть неандертальца от программиста отличает всего лишь ноль?
— Ну вообще введение 0 было огромным шагом для математики. Можно сказать первый мощный шаг к абстрактному мышлению. Так что в какой-то степени да, «0» — это переходная ступень между неандертальцем и программистом.
Нейронные сети. Просто о сложном
Привет, Пикабу. Сегодня у нас кое-что действительно классное для Лиги образования.
Мы договорились о переводе и озвучке с автором самых крутых на Youtube видео про математику-информатику-физику.
И наша первая озвучка — видео о том, что же такое нейросети.
За это отличную озвучку мы благодарим Александра Колдаева.
Если хочешь поучаствовать в переводе или озвучке — напиши нам в вк, телеграм или facebook.
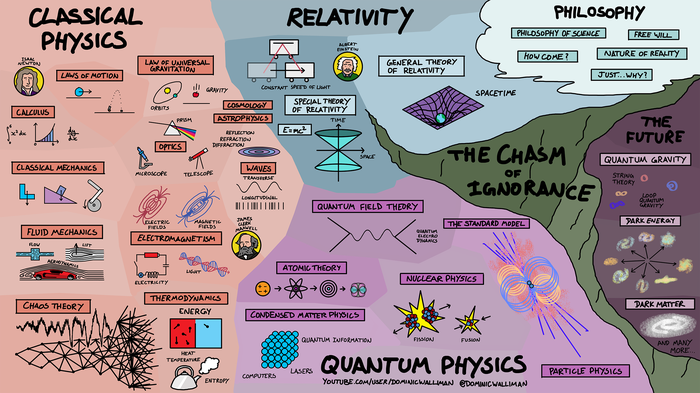
Карты наук
Выше был их автор. А вот и одна из его карт (по физике):
О карте, нарисованной выше, Dominic подробно рассказал в следующем видео. Он рассказал о ранней физике, об Эйнштейне и его теориях специальной и общей относительности, и о подвидах квантовой физики.
Кстати говоря, помимо карт наук, на его странице во flickr есть интересные постеры о том, как мы уже сейчас используем квантовые технологии.
Все его видео по картам наук публикуются в следующем плейлисте: https://www.youtube.com/playlist?list=PLOYRlicwLG3St5aEm02nc.
Они на английском, но уже есть и переводы.
Вот, например, по Computer Science:
А вот по математике:
Спасибо за внимание!
За день до экзамена
Ну, может и не сильно-то ждёт. Ну да ладно, всё равно любит. Наверное.
Что такое двоичные разряды
«Но дружбы нет и той меж нами.
Все предрассудки истребя,
Мы почитаем всех нулями,
А.С.Пушкин «Евгений Онегин»
Изучение языка программирования резонно начать со средств описания данных. Для этого сначала необходимо ввести понятия, касающиеся данных. При изучении Си нам периодически придется опускаться на уровень их машинного представления. Но при первоначальном знакомстве это материал можно пропустить (кроме п. «Типы данных и переменные».), довольствуясь общими представлениями – целое, вещественное, символ, массив.
Системы счисления
Но это еще цветочки. В шестнадцатеричном дампе памяти цифры в байте читаются справа налево, а сами байты целого числа – наоборот. Налицо конфликт цивилизаций.
В понимании взаимоотношения систем счисления важно то, что когда мы говорим о представлении числа в виде цифр, число воспринимается как величина, над которой можно делать какие-то операции, например, складывать с другими. И эта величина не зависит от формы ее представления. Например, мешок сахара остается таковым, независимо от того, как считать его содержимое, в килограммах, пудах или фунтах. Значение сохраняется, а его представление будет разным. Как говорил удав в известном мультике «А в попугаях я значительно длиннее». То же самое касается и операций. Семь спичек плюс семь спичек равно четырнадцати, потому что четырнадцать это десяток и еще четыре (вспомните себя в первом классе).
Преобразование чисел / из одной системы счисления в другую
0.3F516 = 3/16 + 15( F )/16 2 + 5/16 3 = 0.1875 0 + 0.0585 9 + 0.0012 2 = 0.247 31 10
0.5248 = 5/8 + 2/8 2 + 4/8 3 = 0.6250 + 0.0312 + 0.0078 = 0.664010
2301 / 8 = 287 (5) 709 / 16 = 44 (5)
287 / 8 = 35 (7) 44 / 16 = 2 (12= C )
35 / 8 = 4 (3) 2 / 16 = 0 (2) = 2 C 516
0.24731 * 16 = 3.95696 (3)
0.95696 * 16 = 15.31136 (15(F))
0.31136 * 16 = 4. 98176 (4)
0.98176 * 16 = 15.70816 (15( F )) = 0.3 F 4 F16 ≈ 0.3F516
0.968 * 8 = 7.744 (7) = 0.52378 ≈ 0.5248
Обратите внимание, что при преобразовании дробной части сначала в десятичную систему а затем обратно в исходную получаем значение, меньшее исходного, которое только при округлении становится «правильным». Это связано с тем, что при первом преобразовании мы оставили только четыре десятичных цифры, отбросив «хвост».
Двоичная система счисления. Бит, байт, машинное слово
«Но дружбы нет и той меж нами.
Все предрассудки истребя,
А.С.Пушкин «Евгений Онегин»
Общеизвестно, что компьютеры используют двоичную систему. А что это значит, и почему именно ее? Давайте подробнее уточним все «за». Во-первых, она самая технологичная, поскольку элементы с двумя устойчивыми состояниями (да-нет, включено-выключено) самые простые и самые надежные. Во-вторых, алгоритмы выполнения операций в этой системе тоже самые простые. Например, таблица умножения в десятичной системе имеет размерность 10х10, т.е. содержит 100 произведений всех пар цифр, а в двоичной системе всего 4.
100101101 = 2 8 + 2 5 + 2 3 + 2 2 + 2 0 = 256 + 32 + 8 + 4 + 1 = 30110
Естественно, что за простоту эту приходится платить. Как мы уже выяснили, чем меньше основание системы счисления, тем больше цифр требуется для представления заданной величины. Поэтому в двоичной системе число будет иметь максимальную разрядность.
Но двоичная система интересует нас не сама по себе, а как основа внутреннего представления данных в компьютере. Поэтому и появляется соответствующая терминология.
К сожалению, узкотехнический термин «информация» в настоящее время настолько размыт как научными интерпретациями, так и псевдонаучными спекуляциями (типа «ля-ля, тополя, торсионные поля»), поэтому отныне мы будем использовать термин данные. Данные – это такая информация, которую можно представить в компьютере.

2 10 = 1024 ≈ 1000 = 10 3

Эквиваленты двоичной системы
До сих пор мы говорили о системах счисления применительно к представлению и преобразованию в них целых чисел. Поскольку двоичная система – родная для компьютера, как для нас – десятичная, то такие преобразования происходят при вводе и выводе числовых данных. Когда же речь идет о компьютерной архитектуре, внутреннем представлении команд, данных и адресов, десятичная система в общем-то не нужна. Более того, она вредна, потому что размерности данных все равно остаются двоичными. Например, приложение, выполняясь на 32-разрядном процессоре, обращается к памяти, используя адрес – такое же 32-разрядное машинное слово. Кстати, примерно оценить значение адреса можно, подсчитав количество значащих разрядов (отбросив незначащие нули слева).
Не правда ли, напоминает современные банковские реквизиты. К счастью, программисты избавлены от муторной процедуры записи нулей и единичек. Восьмеричная и шестнадцатеричная системы счисления хороши как раз тем, что кратны двоичной. Одна восьмеричная цифра кодирует три двоичных разряда, одна шестнадцатеричная – четыре (тетрада). При этом сама цифра раскладывается как число в двоичное представление по степеням двойки:
Попробуем преобразовать к шестнадцатеричному виду приведенное выше число. В синтаксисе Си шестнадцатеричные числа имеют префикс «0х».
0000 0001 1010 1000 1100 1100 0011 1101
0 1 A 8 C C 3 D = 0x01A8CC3D
На самом деле не совсем так. Мы забыли, что размещение производится младшими байтами вперед, поэтому в любом дампе ( dump – вывод содержимого памяти во внутреннем представлении) Вы увидите все в обратном порядке 3D_CC_A8_01
Получается, что нужно перевернуть не весь дамп, а по отдельности каждую часть, относящуюся к машинному слову. Тут то мы и подходим к фундаментальному свойству памяти: по формальному ее содержимому нельзя определись, что там находится. Все зависит от формата – последовательности размещения данных и их интерпретации. Грубо говоря, на байте или машинном слове не написано, чем они являются.
Форматы базовых типов данных
Возникает резонный вопрос: зачем при программировании на языке высокого уровня и работе с переменными знать их форматы представления в памяти. При программировании на Си/Си++ для этого имеются определенные основания:
· для понимания сущности преобразовании целого со знаком в беззнаковое (и наоборот) требуется иметь представление об их форматах;
· при управлении памятью на низком (физическом) уровне возможен доступ к «составным частям» формата представляемых данных, а также переход от одного типа данных к другому при сохранении содержимого памяти;
· при отладке программ, работающих с двоичными файлами, требуется просматривать двоичные файлы на физическом уровне, при этом форматы представляемых данных в нем идентичны внутренним.
Дополнительный код может быть введен в любой системе счисления. Рассмотрим его работу на привычной нам десятичной:
· вместо знака вводится еще одна цифра слева со значением 0;
· положительные числа представляются обычным образом;
· к полученному значению добавляется 1.
Обратный перевод числа в дополнительном коде происходит тем же самым образом: если старшая цифра – 0, то число положительное и перевод не требуется, иначе число считается отрицательным и для него выполняются два последних пункта процедуры перевода. Рассмотрим пример:
Если внимательно присмотреться, то дополнение каждой цифры до 9 имеет некоторую аналогию с вычитанием. Но как бы там ни было, получаем следующий результат: вычитание или же сложение чисел со знаком заменяется операцией сложения, выполненной для беззнаковых чисел.
В двоичной системе счисления дополнение каждой цифры выглядит как инвертирование двоичного разряда, то есть замена 0 на 1 и наоборот. Тогда получается простой способ представления отрицательного числа:
· абсолютное значение числа в двоичной системе должно занимать все разряды, кроме старшего, последний должен быть 0;
· инвертировать все разряды, включая знаковый;
Ту же самую последовательность операций нужно выполнить, чтобы получить из дополнительного кода абсолютное значение отрицательного числа. В Си это можно сделать и при помощи поразрядных (машинно-ориентированных) операций:
Старший разряд в таком представлении также играет роль знакового. Для отрицательных чисел он равен 1. Рассмотрим, как выглядит представление граничных значений диапазона в шестнадцатеричной системе:
Все эти нюансы вообще-то не важны для программиста, поскольку ему нет нужды вручную выполнять сложение или вычитание ни в двоичной ни в шестнадцатеричной системах, за него это сделает компьютер. На самом деле от программиста даже при работе на уровне внутреннего представления данных достаточно знать правила отображения диапазонов положительных и отрицательных значений знаковых чисел на диапазон беззнаковых. Используемая форма преобразования приводит к тому, что отрицательные числа отображаются на вторую половину диапазона беззнаковых целых, причем таким образом, что значение –1 соответствует максимальному беззнаковому (т.е. 0 xFFFF FFFF во внутреннем представлении), а минимальное отрицательное – середине интервала (т.е. 0 x 80000001). Значение 0 x 80000000 является «водоразделом» положительных и отрицательных и называется «минус 0». Все отрицательные числа имеют старший (знаковый) бит, установленный в 1.
Во внутренним представлении дело обстоит аналогичным образом, но только с учетом двоичного представления всех данных:
На самом деле реальный формат вещественного числа типа double имеет несущественные отличия:
· вместо порядка в формате 11-разрядного беззнакового целого хранится значение p+1023 (всегда положительное);
· в нормализованной мантиссе отбрасываются не только незначащие 0, но и первая значащая 1 (например: 0.0000001 011011… ). Мантисса имеет 52 разряда;
· знак мантиссы представлен отдельным разрядом.
Тип данных и переменная
В языках программирования такие свойства данных, как форма их представления и занимаемая ими память сознательно отделены друг от друга и представлены в виде понятий тип данных и переменная.
Тип данных = формат + размерность, диапазон значений + операции
Переменная в ее первичном архитектурном понимании – это область памяти, в которой содержатся данные определенного типа. Имя переменной напрямую ассоциируется с ее адресом, содержимое памяти – со значением переменной.
Переменная = память (имя, адрес,ссылка) + ТД + значение
Си является языком строго типизированным. Это означает, что использование предварительно не определенных программных объектов, в том числе переменных, не допускается (т.е. невозможна привязка типа автоматически, по умолчанию и т.п).

Базовые типы данных целых чисел
В Си имеется возможность использовать машинные слова различной размерности для определения целых переменных как в знаковой, так и в беззнаковой форме. Для этого используются следующие служебные слова:
Из этих служебных слов можно составить определение типа данных целой переменной. При этом signed считается заданным по умолчанию, а unsigned int сокращается до int:
int i; // целое со знаком, слово
char c; // целое со знаком, байт
unsigned char uc; // целое без знака, байт
unsigned u; // целое без знака, слово
long l; // целое со знаком, двойное слово
unsigned long ul; // целое без знака, двойное слово
short s; // целое со знаком, короткое слово
Для определения размерности различных переменных и типов в Си имеется специальная операция, которая возвращает размерность типа данных, переменной и значения выражения, подсчитанную в байтах:
x = 3; // Присвоить 3 переменной типа digit
Тогда зачем же они нужны? Для придания большей ясности программе: обозначения ограниченного количества вариантов, признаков и т.д..
Массив как производный тип данных
Важная особенность массивов в Си: во время работы программы контроль за нахождением индексов в пределах размерности массива не производится. В случае выхода за пределы массива будут использованы значения переменных в соседних областях памяти и результат работы программы будет непредсказуем.