Что такое двоично десятичная система
Двоично-десятичная система счисления
Вы будете перенаправлены на Автор24
Понятие смешанной системы счисления
Среди систем счисления выделяют класс так называемых смешанных систем счисления.
Примером смешанной системы счисления является двоично-десятичная система.
Практическое обоснование использования двоично-десятичной системы счисления
В некоторых типах ЭВМ в арифметико-логических устройствах (АЛУ) имеются специальные блоки десятичной арифметики, которые выполняют операции над числами, представленными в двоично-десятичном коде. Это позволяет в некоторых случаях существенно повысить производительность ЭВМ.
К примеру, в автоматизированной системе обработки данных используется большое количество чисел, а вычислений при этом немного. В подобном случае операции перевода чисел из одной системы в другую существенно превысили бы время выполнения операций по обработке информации. Микропроцессоры же используют чистые двоичные числа, однако при этом понимают и команды преобразования в двоично-десятичную запись. АЛУ AVR-микроконтроллера (как и других микропроцессоров) выполняет элементарные арифметические и логические операции над числами, представленными в двоичном коде, а именно:
считывает результаты преобразования АЦП;
в формате целых чисел или чисел с плавающей точкой выполняет обработку результатов измерения.
Готовые работы на аналогичную тему
Однако окончательный результат при этом выводится на индикатор в десятичном формате, удобном для восприятия человеком.
Принципы построения двоично-десятичной системы счисления
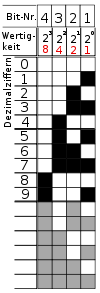
Для записи числа в двоично-десятичной системе счисления его необходимо сначала представить в десятичной системе, а затем каждую, входящую в состав числа, десятичную цифру представить в двоичной системе. При этом для написания различных десятичных цифр в двоичной системе счисления требуется разное количество двоичных разрядов. Чтобы обойтись без применения каких-либо разделительных знаков, при двоичном изображении десятичной цифры всегда записывается 4 двоичных разряда. Группа из этих четырех разрядов называется тетрадой.
$1001 0010 0101_ <(2)>= 2341_<(10)>$,
$1001 0010 0101_ <(2)>= 925_<(2-10)>$.
Как видим, несмотря на то, что сложение осуществлялось в двоичной системе счисления результат операции получился в двоично-десятичной.
Преимущества использования двоично-десятичной системы счисления
Преобразование чисел из десятичной системы в двоично-десятичную систему счисления не связано с вычислениями и его легко реализовать, используя при этом простейшие электронные схемы, так как преобразовывается небольшое количество (4) двоичных цифр. Обратное же преобразование происходит в ЭВМ автоматически с помощью особой программы перевода.
Применение двоично-десятичной системы счисления совместно с одной из основных систем счисления (двоичной) позволяет разрабатывать и создавать высокопроизводительные ЭВМ, так как использование блока десятичной арифметики в АЛУ исключает при решении задач необходимость программированного перевода чисел из одной системы счисления в другую.
Двоично-десятичный код
Двоично-десятичный код (англ. binary-coded decimal ), BCD, 8421-BCD — форма записи целых чисел, когда каждый десятичный разряд числа записывается в виде его четырёхбитного двоичного кода.
Например, десятичное число 31110 будет записано в двоичной системе счисления в двоичном коде как 1 0011 01112, а в двоично-десятичном коде как 0011 0001 0001BCD.
Содержание
Простой способ получения данных в формате BCD из Unsigned Integer
Имеем: Число «A» в формате U16 = 542;
Преобразуем его в BCD: (можно проделать на калькуляторе ОС Windows)
Преимущества и недостатки
Преимущества
По этим причинам двоично-десятичный формат применяется в калькуляторах — калькулятор в простейших арифметических операциях должен выводить в точности такой же результат, какой подсчитает человек на бумаге.
Недостатки
Поэтому, при сложении и вычитании чисел формата 8421-BCD действуют следующие правила:
Пример операции сложения двоично-десятичных чисел:
Требуется: Найти число A = D + C, где D = 3927, C = 4856
Решение: Представим числа D и C в двоично-десятичной форме:
D = 392710 = 0011 1001 0010 0111BCD
C = 485610 = 0100 1000 0101 0110BCD
Суммируем числа D и С по правилам двоичной арифметики:
‘*’ — тетрада, из которой был перенос в старшую тетраду
‘**’ — тетрада с запрещённой комбинацией битов
В тетраду, помеченную символом *, добавляем шестёрку, так как по правилам двоичной арифметики перенос унёс с собой 16, а по правилам десятичной арифметики должен был унести 10. В тетраду, помеченную символом **, добавляем шестёрку и разрешаем распространение переноса, так как комбинация битов 1101 (что соответствует десятичному числу 13) является запрещённой.
См. также
Полезное
Смотреть что такое «Двоично-десятичный код» в других словарях:
Двоично-десятичный код — Код, в котором десятичный разряд числа выражают в двоичном коде Источник … Словарь-справочник терминов нормативно-технической документации
двоично-десятичный код — ДДЕ Метод представления десятичных чисел в двоичном коде в виде групп по четыре бита с весовыми значениями, при чтении слева направо, 8, 4, 2, 1. Примечание Каждая группа представляет одну десятичную цифру, например 0010 0011 23. [ГОСТ 30721… … Справочник технического переводчика
двоично-десятичный код — dvejetainis dešimtainis kodas statusas T sritis automatika atitikmenys: angl. binary decimal code; binary coded decimal code vok. Binärkode für Dezimalziffern, m; binärverschlüsselter Dezimalcode, m rus. двоично десятичный код, m pranc. code BCD … Automatikos terminų žodynas
Расширенный двоично-десятичный код обмена информацией — стандартный восьмибитный код, разработанный корпорацией IBM для присвоения двоичных значений буквам, цифрам, знакам пунктуации и управляющим символам. По английски: Extended Binary Coded Decimal Interchange Code Синонимы английские: EBCDIC См.… … Финансовый словарь
расширенный двоично-десятичный код обмена информацией — 01.01.43 расширенный двоично десятичный код обмена информацией [ extended binary coded decimal interchange code; EBCDIC]: Типовой код, состоящий из 8 битовых кодированных знаков. Примечание В настоящее время указанный код заменяется кодом ASCII.… … Словарь-справочник терминов нормативно-технической документации
расширенный двоично-десятичный код обмена информацией — Восьмибитовый код, используемый в вычислительных машинах фирмы IBM для кодирования знаков. [Л.М. Невдяев. Телекоммуникационные технологии. Англо русский толковый словарь справочник. Под редакцией Ю.М. Горностаева. Москва, 2002] Тематики… … Справочник технического переводчика
Запись десятичных чисел (двоично-десятичный код)
Иногда бывает удобно хранить числа в памяти процессора в десятичном виде (Например, для вывода на экран дисплея). Для записи таких чисел используются двоично-десятичные коды. Не нужно путать двоично-десятичный код с десятичной системой счисления. Для записи одного десятичного разряда используется четыре двоичных бита. Эти четыре бита называются тетрадой. Иногда встречается название, пришедшее из англоязычной литературы: нибл. При помощи четырех бит можно закодировать шестнадцать цифр. Лишние комбинации в двоично-десятичном коде являются запрещенными. Таблица соответствия двоично-десятичного кода и десятичных цифр приведена ниже:
| Двоично-десятичный код | Десятичный код | |||
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 0 | 2 |
| 0 | 0 | 1 | 1 | 3 |
| 0 | 1 | 0 | 0 | 4 |
| 0 | 1 | 0 | 1 | 5 |
| 0 | 1 | 1 | 0 | 6 |
| 0 | 1 | 1 | 1 | 7 |
| 1 | 0 | 0 | 0 | 8 |
| 1 | 0 | 0 | 1 | 9 |
Остальные комбинации двоичного кода в тетраде являются запрещенными. Запишем пример двоично-десятичного кода:
В первой тетраде записана цифра 1, во второй — 2, в третьей — 5, а в последней тетраде записана цифра 8. В данном примере для записи числа 1258 потребовалось четыре тетрады. Количество ячеек памяти микропроцессора зависит от его разрядности. При 16-разрядном процессоре все число уместится в одну ячейку памяти.
В данном примере для записи числа достаточно трех тетрад, но ячейка памяти 16-разрядная. Поэтому старшая тетрада заполняется нулями. Они не изменяют значение цифры. Если бы мы заполнили нулями младшую тетраду, то число увеличилось бы в десять раз!
При записи десятичных чисел часто требуется записывать знак числа и десятичную запятую (в англоязычных странах точку). Двоично-десятичный код часто применяется для набора телефонного номера или набора кодов телефонных служб. В этом случае кроме десятичных цифр часто применяются символы ‘*’ или ‘#’. Для записи этих символов в двоично-десятичном коде применяются запрещенные комбинации
| Двоично-десятичный код | Дополнительный символ | |||
|---|---|---|---|---|
| 1 | 0 | 1 | 0 | * (звёздочка) |
| 1 | 0 | 1 | 1 | # (решётка) |
| 1 | 1 | 0 | 0 | + (плюс) |
| 1 | 1 | 0 | 1 | – (минус) |
| 1 | 1 | 1 | 0 | , (десятичная запятая) |
| 1 | 1 | 1 | 1 | Символ гашения |
Достаточно часто в памяти процессора для хранения одной десятичной цифры выделяется одна ячейка памяти (восьми, шестнадцати или тридцатидвухразрядная). Это делается для повышения скорости работы программы. Для того, чтобы отличить такой способ записи двоично-десятичного числа от стандартного, способ записи десятичного числа, как это показано в примере, называется упакованной формой двоично-десятичного числа. Запишем те же числа, что и в предыдущем примере в неупакованном двоично-десятичном коде для восьмиразрядного процессора:
Суммирование двоично-десятичных чисел.
Понравился материал? Поделись с друзьями!
Другие виды двоичных кодов:
Целочисленные двоичные коды Представление двоичных чисел в памяти компьютера или микроконтроллера
https://digteh.ru/proc/IntCod.php
Представление чисел в двоичном коде с плавающей запятой Стандартные форматы чисел с плавающей запятой для компьютеров и микроконтроллеров
https://digteh.ru/proc/float/
Запись текстов двоичным кодом Представление текстов в памяти компьютеров и микроконтроллеров
https://digteh.ru/proc/text/
Системы счисления В настоящее время и в технике и в быту широко используются как позиционные, так и непозиционные системы счисления.
https://digteh.ru/digital/SysSchis.php
Предыдущие версии сайта:
http://neic.nsk.su/
Об авторе:
к.т.н., доц., Александр Владимирович Микушин
Кандидат технических наук, доцент кафедры САПР СибГУТИ. Выпускник факультета радиосвязи и радиовещания (1982) Новосибирского электротехнического института связи (НЭИС).
А.В.Микушин длительное время проработал ведущим инженером в научно исследовательском секторе НЭИС, конструкторско технологическом центре «Сигнал», Научно производственной фирме «Булат». В процессе этой деятельности он внёс вклад в разработку систем радионавигации, радиосвязи и транкинговой связи.
Научные исследования внедрены в аппаратуре радинавигационной системы Loran-C, комплексов мобильной и транкинговой связи «Сигнал-201», авиационной системы передачи данных «Орлан-СТД», отечественном развитии системы SmarTrunkII и радиостанций специального назначения.
ДВОИЧНО-ДЕСЯТИЧНАЯ СИСТЕМА
Двоично-десятичная система счисления. Десятичные цифры от 0 до 9 заменяются представляющими их двоичными тетрадами: 0=0000, 1=0001, 2=0010, 3=0011, 4=0100, 5=0101, 6=0110, 7=0111, 8=1000 и 9=1001. Такая запись очень часто используется как промежуточный этап перевода числа из десятичной системы в двоичную или обратно. Так как 10 не является точной степенью 2, то используются не все 16 тетрад, а алгоритмы арифметических операций над многозначными числами здесь более сложны, чем в основных системах счисления. И тем не менее, двоично-десятичная система счисления применяется даже на этом уровне во многих микрокалькуляторах и некоторых компьютерах (в частности, «Ямаха» стандарта MSX).
Принцип построения этой системы достаточно прост: каждая десятичная цифра преобразуется прямо в свой десятичный эквивалент из 4 бит, например: 369110=0011 0110 1001 0001DEC:
Десятичное число 3 6 9 1 Двоично-десятичное число 0011 0110 1001 0001
Преобразуем двоично-десятичное число 1000 0000 0111 0010 в его десятичный эквивалент. Каждая группа из 4 бит преобразуется в её десятичный эквивалент. Получим 1000 0000 0111 0010DEC = 807210:
Двоично-десятичное число 1000 0000 0111 0010 Десятичное число 8 0 7 2
Микропроцессоры используют чистые двоичные числа, однако понимают и команды преобразования в двоично-десятичную запись. Полученные двоично-десятичные числа легко представимы в десятичной записи, более понятной людям.
Преобразование двоичных чисел в двоично-десятичные
Арифметико-логическое устройство AVR-микроконтроллеров (как и других микропроцессоров) выполняет элементарные арифметические и логические операции над числами, представленными в двоичном коде. В двоичном коде считываются результаты преобразования АЦП, в двоичном коде (в формате целых чисел или чисел с плавающей точкой) удобно выполнять обработку результатов измерения. Однако, когда окончательный результат отображается на индикаторе, он должен быть преобразован в десятичный формат, удобный для восприятия человеком.
В данном разделе рассматриваются программы преобразования двоичных чисел в двоично-десятичные.
1. Форматы представления десятичных чисел
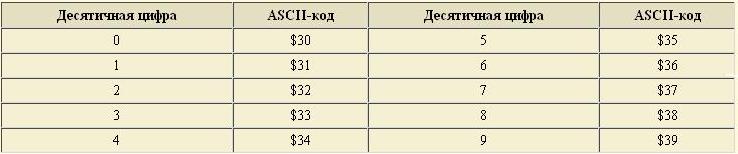
Неупакованный десятичный код является подмножеством международной таблицы кодирования символов ASCII (Таблица 1). Видно, что для хранения неупакованных десятичных чисел требуется в два раза больше памяти, так как каждая цифра представляется 8-битным кодом. Таблица 1: ASCII-коды десятичных цифр
2. Преобразование целых 16-битных чисел в двоично-десятичные числа
На сайте www.atmel.com предлагается программа «bin2bcd16» для преобразования целых 16-битных двоичных чисел в двоично-десятичные упакованные числа. В данной статье рассматривается программа «bin16bcd5» (см. Приложение, Программа 1), написанная Терешкиным А. В. согласно алгоритму, изложенному в [1], и выполняющая ту же задачу. Последняя программа по быстродействию, длине кода и количеству используемых регистров оказалась более эффективной, чем первая.
Алгоритм программы «bin16bcd5» заключается в следующем. Предположим, что имеется целое беззнаковое 16-битное число (диапазон от 0 до 65535). Очевидно, что необходимо найти 5 десятичных цифр. Способ преобразования заключается в том, чтобы, вычитая из исходного числа число 10000, сначала определить десятичную цифру десятков тысяч. Затем находится цифра тысяч последовательным вычитанием числа 1000 и т. д. Вычитание каждый раз производится до получения отрицательной разности с подсчетом числа вычитаний. При переходе к определению каждого следующего десятичного разряда в регистрах исходного числа восстанавливается последняя положительная разность. После того, как будет найдена десятичная цифра десятков, в регистрах исходного числа останется десятичная цифра единиц.
Программа «bin16ASCII5» (см. Приложение, Программа 2) преобразует целое двоичное 16-битное число в десятичное неупакованное число. При этом используется тот же алгоритм.
3. Преобразование двоичной дроби в двоично-десятичную дробь
Двоичная дробь, по определению, представляется следующим выражением:
Из этого представления следует алгоритм преобразования (Рис. 2), который содержит m шагов. На каждом шаге к двоично-десятичному результату прибавляется очередная двоичная цифра и весь результат делится на 2.
На изображены двоичный регистр, который содержит исходную двоичную дробь и регистр двоично-десятичного упакованного результата. Для наглядности у обоих регистров также показаны разряд единиц и положение точки, которые в памяти микропроцессора никак не представлены, но положение которых всегда строго оговорено. Количество циклов рассматриваемого алгоритма равно количеству бит двоичной дроби. Разрядность двоично-десятичного регистра определяется требуемой точностью вычислений.
Сложить эту цифру с двоично-десятичным числом означает, что ее нужно поместить в разряд единиц двоично-десятичного числа, откуда при последующем делении на два цифра A-i сдвинется в старший разряд старшей тетрады десятичной дроби. При программировании мы можем представлять, что разрядом единиц десятичной дроби является бит переноса С.
При делении на два двоично-десятичного упакованного числа, так же как и при делении двоичного числа, его сдвигают вправо на один разряд. При этом на два делится каждая тетрада, то есть каждая десятичная цифра. При делении четной десятичной цифры в соответствующем разряде снова получается десятичная цифра, и никакой коррекции не требуется. При делении на 2 нечетной десятичной цифры остаток, равный 5, должен быть добавлен к более младшему десятичному разряду, но на самом деле при двоичном сдвиге в более младшую тетраду добавляется число 8 (вес старшего разряда тетрады). Поэтому требуется коррекция результата, которая заключается в вычитании числа 3 из содержимого тех тетрад, которые после сдвига вправо имеют установленные старшие разряды.
4. Преобразование чисел с плавающей точкой в двоично-десятичные числа
Представление чисел с плавающей точкой имеет следующий вид:
Такое представление часто используется и в десятичной системе счисления для представления очень больших или очень малых чисел. Мантисса и порядок представляют собой целые знаковые числа. Знак мантиссы является знаком всего числа. Порядок показывает истинное положение точки вместо того, которое она занимает в изображении мантиссы. Двоичное число с плавающей точкой отличается от привычного нам десятичного тем, что точка является двоичной, то есть порядок показывает на количество двоичных (а не десятичных) разрядов, на которое необходимо переместить эту точку влево или вправо.
Нормализованным представлением числа с плавающей точкой называют такое представление, когда мантисса является правильной дробью, и старшая ее цифра отличается от нуля. Но для двоичного числа требование того, что старшая цифра отличается от нуля означает, что эта цифра равна 1. Если старшая цифра точно известна, то ее можно не хранить в памяти.
Двоично-десятичная система счисления
Обозначение смешанной системы счисления
В мире электронно-вычислительных технологий существуют различные системы счислений. Одним из классов систем счисления является класс смешанной системы счисления.
Таких систем существует несколько, одной из них является двоично-десятичная система счисления.
Построение в двоично-десятичной системе
В этой записи используются четверки цифр двоично-десятичной системы, которые последовательно отображают цифры 9, 2 и 5. Эти последовательные четверки цифр называются тетрадами.
В двоичной системе для изображения чисел также используются 0 и 1, но невзирая на это, изображения десятичного числа в двоично-десятичной системе отличается от его записи в двоичной системе счисления. К примеру, та же запись 100100100101 в этих двух системах будет обозначать разное десятичное число. Это выглядит так:
Подобное изображение числа зачастую используется в качестве вспомогательного этапа при трансформации числа из двоичной в десятичную систему счисления и наоборот. В двоично-десятичной системе счисления алгоритмы арифметических вычислений многозначных чисел намного сложнее, чем в простых системах счисления, но тем не менее эта система счисления часто используется для этих операций в микросхемах компьютеров и калькуляторов.
Сложно разобраться самому?
Попробуй обратиться за помощью к преподавателям
При корректировке результатов элементарных арифметических операций с числами, записанными с помощью двоично-десятичных кодов, используют специальные команды для преобразования их в двоично-десятичную систему счисления. В данном случае применяется правило: для получения в результате простой арифметической операции сложения или вычитания число в тетраде, большее чем 9, к ней нужно прибавить число 6. Такое уравновешивание по разрядам производится обычно с помощью двоично-десятичной системы счисления. При этом самым целесообразным является комплексное использование двоичной и двоично-десятичной систем счисления, так как при этом количество тактов уравновешивания намного меньшее, чем при использовании иных систем счисления.
Для чего нужно использование двоично-десятичной системы счисления
Человеческому глазу понятна десятичная система изображения чисел, и мы используем ее практически в любой сфере жизни, где сталкиваемся с числами. Работа электроники построена на использовании двоичной системы вывода чисел. Поэтому вариант применения системы счисления с помощью двоично-десятичных кодов является компромиссным. Двоично-десятичные коды используется в тех микросхемах приборов, где есть потребность частого ввода и вывода десятичных чисел, к примеру, в электронных часах, калькуляторах, таймерах, дисплеях бытовой техники и прочих приборах, в которых нет смысла использовать универсальные микрокоды из-за ограниченного объема памяти.
В арифметических логических устройствах электронно-вычислительных машин есть специальные блоки арифметических вычислений, выполняющих операции на основании двоично-десятичной системы счисления. Во многих случаях это существенно повышает производительность электронно-вычислительных машин. Например, если рассмотреть системы автоматизированной обработки данных, в которых практически не используются арифметические вычисления, то процесс трансформации чисел из одной системы в другую занял бы длительный ресурс времени и памяти. Поэтому в микропроцессорах в таком случае применяются двоичные коды, но при этом они умеют распознавать команды трансформации в двоично-десятичные коды. В итоге результат изображается на дисплее в десятичной форме изображения числа, понятной человеку.
Выгоды применения двоично-десятичной системы
Применение двоично-десятичной системы счисления в комплексе с двоичной системой, которая является одной из основных, позволяет создавать на рынке высокопроизводительные электронно-вычислительные машины. Это становится возможным благодаря применению блока десятичных арифметических операций без необходимости программного трансформирования чисел в двоичную систему.
Не нашли что искали?
Просто напиши и мы поможем
Трансформация чисел в двоично-десятичную систему из десятичной не требует громоздких арифметических вычислений, а является простой операцией с использованием четырехразрядных кодов тетрад, что производится автоматически при помощи элементарных алгоритмических программ.
Так как две двоично-десятичные цифры в сумме занимают всего 1 байт памяти, то с его помощью можно записать любую десятичную цифру от 0 до 99. Таким образом, используя всего лишь 1 байт для изображения двух любых десятичных цифр, возможно записать любое количество двоично-десятичных чисел с необходимым количеством десятичных разрядов.
Не нашли нужную информацию?
Закажите подходящий материал на нашем сервисе. Разместите задание – система его автоматически разошлет в течение 59 секунд. Выберите подходящего эксперта, и он избавит вас от хлопот с учёбой.
Гарантия низких цен
Все работы выполняются без посредников, поэтому цены вас приятно удивят.
Доработки и консультации включены в стоимость
В рамках задания они бесплатны и выполняются в оговоренные сроки.
Вернем деньги за невыполненное задание
Если эксперт не справился – гарантируем 100% возврат средств.
Тех.поддержка 7 дней в неделю
Наши менеджеры работают в выходные и праздники, чтобы оперативно отвечать на ваши вопросы.
Тысячи проверенных экспертов
Мы отбираем только надёжных исполнителей – профессионалов в своей области. Все они имеют высшее образование с оценками в дипломе «хорошо» и «отлично».
Гарантия возврата денег
Эксперт получил деньги, а работу не выполнил?
Только не у нас!
Деньги хранятся на вашем балансе во время работы над заданием и гарантийного срока
Гарантия возврата денег
В случае, если что-то пойдет не так, мы гарантируем возврат полной уплаченой суммы