Что такое двоичная система счисления
Двоичное счисление на пальцах
Все знают, что компьютеры состоят из единиц и нулей. Но что это значит на самом деле?
Если у вас в школе была информатика, не исключено, что там было упражнение на перевод обычных чисел в двоичную систему и обратно. Маловероятно, что кто-то вам объяснял практический смысл этой процедуры и откуда вообще берётся двоичное счисление. Давайте закроем этот разрыв.
Эта статья не имеет практической ценности — читайте её просто ради интереса к окружающему миру. Если нужны практические статьи, заходите в наш раздел «Где-то баг», там каждая статья — это практически применимый проект.
Отличный план
Чтобы объяснить всё это, нам понадобится несколько тезисов:
Система записи — это шифр
Если у нас есть девять коров, мы можем записать их как 🐄🐄🐄🐄🐄🐄🐄🐄🐄 или как 9 × 🐄.
Почему 9 означает «девять»? И почему вообще есть такое слово? Почему такое количество мы называем этим словом? Вопрос философский, и короткий ответ — нам нужно одинаково называть числа, чтобы друг друга понимать. Слово «девять», цифра 9, а также остальные слова — это шифр, который мы выучили в школе, чтобы друг с другом общаться.
Допустим, к нашему стаду прибиваются еще 🐄🐄🐄. Теперь у нас 🐄🐄🐄🐄🐄🐄🐄🐄🐄🐄🐄🐄 — двенадцать коров, 12. Почему мы знаем, что 12 — это «двенадцать»? Потому что мы договорились так шифровать числа.
Нам очень легко расшифровывать записи типа 12, 1920, 100 500 и т. д. — мы к ним привыкли, мы учили это в школе. Но это шифр. 12 × 🐄 — это не то же самое, что 🐄🐄🐄🐄🐄🐄🐄🐄🐄🐄🐄🐄. Это некая абстракция, которой мы пользуемся, чтобы упростить себе счёт.
Мы привыкли шифровать десятью знаками
У нас есть знаки 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9 — всего десять знаков. Этим числом знаков мы шифруем количество единиц, десятков, сотен, тысяч и так далее.
Мы договорились, что нам важен порядок записи числа. Мы знаем, что самый правый знак в записи означает число единиц, следующий знак (влево) означает число десятков, потом сотен и далее.
Например, перед нами число 19 547. Мы знаем, что в нём есть:
Если приглядеться, то каждый следующий разряд числа показывает следующую степень десятки:
Нам удобно считать степенями десятки, потому что у нас по десять пальцев и мы с раннего детства научились считать до десяти.
Система записи — это условность
Представим бредовую ситуацию: у нас не 10 пальцев, а 6. И в школе нас учили считать не десятками, а шестёрками. И вместо привычных цифр мы бы использовали знаки ØABCDE. Ø — это по-нашему ноль, A — 1, B — 2, E — 5.
Вот как выглядели бы привычные нам цифры в этой бредовой системе счисления:
| 0 — Ø 1 — A 2 — B 3 — C 4 — D 5 — E | 6 — AØ 7 — AA 8 — AB 9 — AC 10 — AD 11 — AE | 12 — BØ 13 — BA 14 — BB 15 — BC 16 — BD 17 — BE | 18 — CØ 19 — CA 20 — CB 21 — CC 22 — CD 23 — CE | 24 — DØ 25 — DA 26 — DB 27 — DC 28 — DD 29 — DE | 30 — EØ 31 — EA 32 — EB 33 — EC 34 — ED 35 — EE | 36 — AØØ 37 — AØA 38 — AØB 39 — AØC 40 — AØD 41 — AØE |
В этой системе мы считаем степенями шестёрки. Число ABADØ можно было бы перевести в привычную нам десятичную запись вот так:
A × 6 4 = 1 × 1296 = 1296
B × 6 3 = 2 × 216 = 432
1296 + 432 + 36 + 24 + 0 = 1788. В нашей десятичной системе это 1788, а у людей из параллельной вселенной это ABADØ, и это равноценно.
Выглядит бредово, но попробуйте вообразить, что у нас в сумме всего шесть пальцев. Каждый столбик — как раз шесть чисел. Очень легко считать в уме. Если бы нас с детства учили считать шестёрками, мы бы спокойно выучили этот способ и без проблем всё считали. А счёт десятками вызывал бы у нас искреннее недоумение: «Что за бред, считать числом AD? Гораздо удобнее считать от Ø до E!»
То, как мы шифруем и записываем числа, — это следствие многовековой традиции и физиологии. Вселенной, космосу, природе и стадам коров глубоко безразлично, что мы считаем степенями десятки. Природа не укладывается в эту нашу систему счёта.
Двоичная система (тоже нормальная)
Внутри компьютера работают транзисторы. У них нет знаков 0, 1, 2, 3… 9. Транзисторы могут быть только включёнными и выключенными — обозначим их 💡 и ⚫.
Мы можем научить компьютер шифровать наши числа этими транзисторами так же, как шестипалые люди шифровали наши числа буквами. Только у нас будет не 6 букв, а всего две: 💡 и ⚫. И выходит, что в каждом разряде будет стоять не число десяток в разной степени, не число шестёрок в разной степени, а число… двоек в разной степени. И так как у нас всего два знака, то получается, что мы можем обозначить либо наличие двойки в какой-то степени, либо отсутствие:
9 — 💡 ⚫⚫ 💡
10 — 💡 ⚫ 💡 ⚫
11 — 💡 ⚫ 💡 💡
12 — 💡 💡 ⚫⚫
13 — 💡 💡 ⚫ 💡
14 — 💡 💡 💡 ⚫
15 — 💡 💡 💡 💡
17 — 💡 ⚫⚫⚫ 💡
18 — 💡 ⚫⚫ 💡 ⚫
19 — 💡 ⚫⚫ 💡 💡
20 — 💡 ⚫ 💡 ⚫⚫
21 — 💡 ⚫ 💡 ⚫ 💡
21 — 💡 ⚫ 💡 💡 ⚫
23 — 💡 ⚫ 💡 💡 💡
24 — 💡 💡 ⚫⚫⚫
25 — 💡 💡 ⚫⚫ 💡
26 — 💡 💡 ⚫ 💡 ⚫
27 — 💡 💡 ⚫ 💡 💡
28 — 💡 💡 💡 ⚫⚫
29 — 💡 💡 💡 ⚫ 💡
30 — 💡 💡 💡 💡 ⚫
31 — 💡 💡 💡 💡 💡
33 — 💡 ⚫⚫⚫⚫ 💡
34 — 💡 ⚫⚫⚫ 💡 ⚫
35 — 💡 ⚫⚫⚫ 💡 💡
36 — 💡 ⚫⚫ 💡 ⚫⚫
37 — 💡 ⚫⚫ 💡 ⚫ 💡
38 — 💡 ⚫⚫ 💡 💡 ⚫
39 — 💡 ⚫⚫ 💡 💡 💡
40 — 💡 ⚫ 💡 ⚫⚫⚫
41 — 💡 ⚫ 💡 ⚫⚫ 💡
42 — 💡 ⚫ 💡 ⚫ 💡 ⚫
43 — 💡 ⚫ 💡 ⚫ 💡 💡
44 — 💡 ⚫ 💡 💡 ⚫⚫
45 — 💡⚫💡💡⚫💡
46 — 💡⚫💡💡💡⚫
47 — 💡⚫💡💡💡💡
48 — 💡💡⚫⚫⚫⚫
49 — 💡💡⚫⚫⚫💡
50 — 💡💡⚫⚫💡⚫
51 — 💡💡⚫⚫💡💡
52 — 💡💡⚫💡⚫⚫
53 — 💡💡⚫💡⚫💡
54 — 💡💡⚫💡💡⚫
55 — 💡💡⚫💡💡💡
56 — 💡💡💡⚫⚫⚫
57 — 💡💡💡⚫⚫💡
58 — 💡💡💡⚫💡⚫
59 — 💡💡💡⚫💡💡
60 — 💡💡💡💡⚫⚫
61 — 💡💡💡💡⚫💡
62 — 💡💡💡💡💡⚫
63 — 💡💡💡💡💡💡
Если перед нами число 💡 ⚫💡⚫⚫ 💡💡⚫⚫, мы можем разложить его на разряды, как в предыдущих примерах:
256 + 0 + 64 + 0 + 0 + 8 + 4 + 0 + 0 = 332
Получается, что десятипалые люди могут записать это число с помощью цифр 332, а компьютер с транзисторами — последовательностью транзисторов 💡⚫💡⚫⚫ 💡💡⚫⚫.
Если теперь заменить включённые транзисторы на единицы, а выключенные на нули, получится запись 1 0100 1100. Это и есть наша двоичная запись того же самого числа.
Почему говорят, что компьютер состоит из единиц и нулей (и всё тлен)
Инженеры научились шифровать привычные для нас числа в последовательность включённых и выключенных транзисторов.
Дальше эти транзисторы научились соединять таким образом, чтобы они умели складывать зашифрованные числа. Например, если сложить 💡⚫⚫ и ⚫⚫💡, получится 💡⚫💡. Мы писали об этом подробнее в статье о сложении через транзисторы.
Дальше эти суммы научились получать супербыстро. Потом научились получать разницу. Потом умножать. Потом делить. Потом всё это тоже научились делать супербыстро. Потом научились шифровать не только числа, но и буквы. Научились их хранить и считывать. Научились шифровать цвета и координаты. Научились хранить картинки. Последовательности картинок. Видео. Инструкции для компьютера. Программы. Операционные системы. Игры. Нейросети. Дипфейки.
И всё это основано на том, что компьютер умеет быстро-быстро складывать числа, зашифрованные как последовательности включённых и выключенных транзисторов.
При этом компьютер не понимает, что он делает. Он просто гоняет ток по транзисторам. Транзисторы не понимают, что они делают. По ним просто бежит ток. Лишь люди придают всему этому смысл.
Когда человека не станет, скорость света будет по-прежнему 299 792 458 метров в секунду. Но уже не будет тех, кто примется считать метры и секунды. Такие дела.
Как объяснять двоичную систему счисления
Кто-то только входит в IT-мир, кто-то объясняет информатику своему чаду.
Довольно быстро вы обнаружите, что не так-то просто объяснить, как работает двоичный счёт.
Это вам очевидно, что после 11 идёт 100, а новичку это ещё долго может быть непонятно.
Так вот, чтобы увеличить скорость понимания, мы решили сделать дидактический материал.
Проблема
Важно отметить, что даже распиаренный курс Гарвардского университета по компьютерным наукам «CS50» не помогает.
Парень из американского университета просто заявляет, что «нуль — это нуль», «один — это один», а потом идёт 10, а потом 11. Понятно? Думаю, нет. Вот спросите кого-то, кто не программист, а каким будет следующее число — высока вероятность, что он не сможет ответить. Слишком быстро проскочили идею о переносе разряда.
То же самое касается школьных методов перевода: во-первых, методы эти академически сухи, во-вторых, не интуитивны — например, не очевидно, почему после каскадного деления на 2 нужно ставить биты задом наперёд.
А если непонятно, то и не интересно. А если нет интереса, то и запоминается с трудом.
Мы это всё учли, и решили сделать интересное и постепенное объяснение.
Что мы предлагаем
Сначала нужно объяснить, как вообще работает обычная десятичная система счисления — и про конечный «алфавит» цифр, и про идею переноса разряда. Так развивается понимание принципа «системы счисления».
Только потом можно переходить к идее двоичной системы — и вот обучаемый уже медленно, но довольно уверенно говорит «1, 10, 11, 100».
Далее, мы решили попробовать совсем не школьный метод — объяснение двоичного счёта на пальцах: это когда загнутый палец это 0, а разогнутый это 1.
Я проверял это на подростках: показываешь им: «это 1, это 2, это 3 — теперь покажите мне 4». И весь класс сосредоточенно, медленно показывает средние пальцы. Отличницы в эсхатологическом восторге, задние парты тыкают друг другу в лицо и кричат «на тебе четвёрку!».
Провокативно? Да. Запоминается? 100%.
Теперь, когда тема стала «своей», можно переходить к теме перевода чисел из одной системы счисления в другую — начать лучше с классического школьного сухого перевода (если честно, то больше чтобы постращать).
А уже потом с помощью анимации объяснить идею перевода прямо на пальцах, и потом опять же на пальцах пересчитать число 132 в средние пальцы уже на обеих руках.
На десерт показываем, где двоичная и 16-ричная системы применяется в реальной жизни.
Двоичная система — это например QR-коды вокруг нас.
А 16-ричная система это в основном коды цветов в CSS и хеши разных стилей, от MD5 до UUID.
Итак, вот весь пакет видео-уроков (они бесплатные, в Ютубе):
Двоичная система исчисления
Здравствуйте, в этой статье мы поговорим про такую важную тему, как двоичная система исчисления, называемую также бинарным кодом. Всем, кто хочет идти работать в ай-ти сферу должны обязательно разобраться в этом разделе, а для всех остальных будет полезно ознакомиться для общего развития, с представленной ниже информацией.
Я попытаюсь дать все необходимые понятия, и попытаюсь подробно разжевать их, чтобы у вас не осталось никаких вопросов. Попробую дополнить всё примерами, а самые сложные моменты попытаюсь объяснить на пальцах. После прочтения вы узнаете о представлении чисел в двоичном коде, некоторые особенности и полезные свойства этой системы счисления, отрасли, где она применяется и краткую теорию её становления в информатике.
Экскурс в прошлое
Минимально необходимый теоретический базис
Для того чтобы полностью разобраться с двоичным исчислением нужно разобрать, или повторить основные определения. Это будет фундаментом для того, чтобы вы смогли понять то, что дальше написано. К ним относятся такие понятия как:
Понимая все то, что написано выше, можно перейти к сути вопроса. Итак:
Двоичная система счисления – позиционная система с основанием 2. Для отображения чисел применяется два знака – 0 и 1.
В математике обозначается с помощью нижнего индекса, где указано основание. Выглядит это вот так 
Немного про то, что значат буквы в формуле:
Практика
Без практики объяснить, как этим пользоваться – трудно. Поэтому рассмотрим пару примеров. Однако для начала вам необходимо скачать таблицу, где значения бинарного кода представляются в десятичной форме. Я взял первую попавшуюся таблицу с интернета. Выглядеть она будет примерно так:
Задача 1: Представить 7 в двоичном коде, а потом расписать его с помощью формулы выше.
Для того чтобы это сделать надо:
Как видно из примера здесь нет ничего сложного. Давайте разберем что-нибудь посложнее, да и найдем таблицу посерьезнее. Я взял вот такую:
Задача 2: отобразить 13 в двоичной системе счисления.
Все шаги останутся точно такими же, однако я покажу другой способ для выполнения первого пункта. Принцип тот же, но он кажется мне более удобным.
Получаем что
Смотрим что в таблице:
Далее я приведу несколько свойств, которые вы сможете применить при работе с двоичной системой.
Полезные свойства
Области применения
Заключение
На этом всё, вот вы и познакомились с двоичной системой исчисления. Здесь мы рассмотрели общие положения и научились пользоваться таблицей для проверки результатов. Также вы знаете отрасли применения. Прочитав другие материалы нашего сайта, вы сможете научиться выполнять арифметические операции, и переводить счисление с основанием два в другие нумерации. Например шестнадцатеричную и восьмеричную (основание шестнадцать и восемь). При возникновении вопросов оставляйте их в комментариях.
Двоичная система
Двоичная система счисления — это позиционная система счисления с основанием 2. В этой системе счисления натуральные числа записываются с помощью всего лишь двух символов (в роли которых обычно выступают цифры 0 и 1).
Двоичная система используется в цифровых устройствах, поскольку является наиболее простой и соответствует требованиям:
В цифровой электронике одному двоичному разряду в двоичной системе счисления соответствует один двоичный логический элемент (инвертор с логикой на входе) с двумя состояниями (открыт, закрыт).
Содержание
Таблица умножения двоичных чисел
Использование двоичной системы при измерении дюймами
При указании линейных размеров в дюймах по традиции используют двоичные дроби, а не десятичные, например: 5¾″, 7 15 / 16″, 3 11 / 32″ и т. д.
Преобразование чисел
Для преобразования из двоичной системы в десятичную используют следующую таблицу степеней основания 2:
| 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
Начиная с цифры 1 все цифры умножаются на два. Точка, которая стоит после 1 называется двоичной точкой.
Преобразование двоичных чисел в десятичные
Допустим, вам дано двоичное число 110011. Какому числу оно эквивалентно? Чтобы ответить на этот вопрос, прежде всего запишите данное число следующим образом:
| 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 1 | 1 | 0 | 0 | 1 | 1 | ||||
| 32 | +16 | +2 | +1 |
Затем, начиная с двоичной точки, двигайтесь влево. Под каждой двоичной единицей напишите её эквивалент в строчке ниже. Сложите получившиеся десятичные числа. Таким образом, двоичное число 110011 равнозначно 51.
Либо 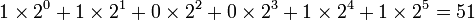
Преобразование методом Горнера
Для того, что бы преобразовывать числа из двоичной в десятичную систему данным методом, надо суммировать цифры слева-направо, умножая ранее полученный результат на основу системы (в данном случае 2). Например, двоичное число 1011011 переводится в десятичную систему так: 0*2+1=1 >> 1*2+0=2 >> 2*2+1=5 >> 5*2+1=11 >> 11*2+0=22 >> 22*2+1=45 >> 45*2+1=91 То есть в десятичной системе это число будет записано как 91. Или число 101111 переводится в десятичную систему так: 0*2+1=1 >> 1*2+0=2 >> 2*2+1=5 >> 5*2+1=11 >> 11*2+1=23 >> 23*2+1=47 То есть в десятичной системе это число будет записано как 47.
Преобразование десятичных чисел к ближайшей степени двойки, неменьшей этого числа
Ниже приведена функция, возвращающая число, неменьшее аргумента, и являющееся степенью двух.
Преобразование десятичных чисел в двоичные
Допустим, нам нужно перевести число 19 в двоичное. Вы можете воспользоваться следующей процедурой :
Итак, мы делим каждое частное на 2 и записываем в остаток 1 или 0. Продолжать деление надо пока в делимом не будет 1. Ставим числа из остатка друг за другом, начиная с конца. В результате получаем число 19 в двоичной записи (начиная с конца): 10011.
Другие системы счисления
В статье «Системы счисления (продолжение)» [1] описываются преимущества и недостатки 4-ричной системы счисления по сравнению с двоичной в компьютерах, созданных Хитогуровым.
См. также
Ссылки
Полезное
Смотреть что такое «Двоичная система» в других словарях:
ДВОИЧНАЯ СИСТЕМА — ДВОИЧНАЯ СИСТЕМА, в математике система счисления, имеющая ОСНОВАНИЕ 2 (десятичная система имеет основание 10). Она наиболее пригодна для работы с компьютерами, поскольку отличается простотой и соответствует двум положениям (открытое 0 и закрытое… … Научно-технический энциклопедический словарь
двоичная система — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN binary system … Справочник технического переводчика
двоичная система — dvejetainė sistema statusas T sritis automatika atitikmenys: angl. binary system vok. Binärsystem, n rus. двоичная система, f pranc. système binaire, m … Automatikos terminų žodynas
двоичная система — dvejetainė sistema statusas T sritis fizika atitikmenys: angl. binary system; dyadic system vok. Binärsystem, n; Dualsystem, n rus. двоичная система, f pranc. système binaire, m … Fizikos terminų žodynas
Двоичная система — Жарг. студ. Шутл. Сильное опьянение. ПБС, 2002 … Большой словарь русских поговорок
Двоичная система счисления — позиционная система счисления с основанием 2, в которой для записи чисел используются цифры 0 и 1. См. также: Позиционные системы счисления Финансовый словарь Финам … Финансовый словарь
ДВОИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ — ДВОИЧНАЯ система СЧИСЛЕНИЯ, способ записи чисел, при котором используются две цифры 0 и 1. Две единицы 1 го разряда (т.е. места, занимаемого в числе) образуют единицу 2 го разряда, две единицы 2 го разряда образуют единицу 3 го разряда и т.д.… … Современная энциклопедия
Двоичная система счисления — ДВОИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ, способ записи чисел, при котором используются две цифры 0 и 1. Две единицы 1 го разряда (т.е. места, занимаемого в числе) образуют единицу 2 го разряда, две единицы 2 го разряда образуют единицу 3 го разряда и т.д.… … Иллюстрированный энциклопедический словарь
Двоичная система исчисления — система, использующая для представления буквенно цифровых и иных символов наборы комбинаций цифр 1 и 0, основа используемых в цифровых ЭВМ кодов … Издательский словарь-справочник
ДВОИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ — позиционная система счисления с основанием 2, в которой имеются две цифры 0 и 1, и их последовательностями записываются все натуральные числа. Напр. цифра 2 записывается как 10, цифра 4 = 22 как 100, число 900 как 11 значное число: 11 110 101 000 … Большая политехническая энциклопедия
Двоичная система счисления
Двоичная система — это один из видов позиционных систем счисления. Основание данной системы равно двум, то есть используется только два символа для записи чисел.
Немного истории
Впервые о данной системе чисел заговорил основоположник математического анализа Г.В. Лейбниц еще в XVII веке. Он доказал, что для данного множества действуют все арифметические операции: сложение, вычитание, умножение и даже деление. Однако вплоть до 30-х годов XX века данную систему не рассматривали всерьез. Но с развитием электронных устройств и ЭВМ, ученые вновь принялись к изучению данной темы, так как двоичная система отлично подходила для программирования и организации хранения данных в памяти компьютеров.
Таблица и алфавит
Кроме того, двоичная система является самой удобной для быстрого перевода в другие системы счисления.
1001102 = 1 ∙ 2 5 + 0 ∙ 2 4 + 0 ∙ 2 3 + 1 ∙ 2 2 + 1 ∙ 2 2 + 0 ∙ 2 0 = 32 + 0 + 0 + 4 + 2 + 0 = 3810
Чтобы наоборот перевести число в двоичную из десятичной, необходимо выполнить его деление на 2 с остатком, а затем записать все остатки в обратном порядке, начиная с частного:
| Делимое | 38 | 19 | 9 | 4 | 2 |
|---|---|---|---|---|---|
| Делитель | 2 | 2 | 2 | 2 | 2 |
| Частное | 19 | 9 | 4 | 2 | 1 |
| Остаток | 0 | 1 | 1 | 0 | 0 |
Для перевода в другие системы необходимо:
Однако можно воспользоваться и более быстрым и удобным способом: разделить знаки двоичного числа на условные группы слева на право (для восьмеричной — по 3 знака; для шестнадцатеричной — по 4 знака), а затем воспользоваться таблицей перевода:
| Двоичная | Восьмеричная | Шестнадцатеричная |
|---|---|---|
| 0 | 0 | 0 |
| 001 | 1 | 1 |
| 010 | 2 | 2 |
| 011 | 3 | 3 |
| 100 | 4 | 4 |
| 101 | 5 | 5 |
| 110 | 6 | 6 |
| 111 | 7 | 7 |
| 1000 | 8 | |
| 1001 | 9 | |
| 1010 | A | |
| 1011 | B | |
| 1100 | C | |
| 1101 | D | |
| 1110 | E | |
| 1111 | F |
110010012 = 11 001 001 = 011 001 001 = 3118
110010012 = 1100 1001 = С916
Представление двоичных чисел
В двоичной системе также существует понятие «отрицательных» чисел. И для того, чтобы провести какую-либо операцию с ними в двоичном коде, необходимо представить его в виде дополнительного кода. Запись положительного числа при этом не меняется ни для одного из кодов.
Чтобы найти дополнительный код отрицательного числа, необходимо воспользоваться его прямым и дополнительным кодами.
Прямой код предполагает приписывание единицы в начале без изменений записи:
| A > 0 | Aпр = 0A | 1010112; Aпр = 01010112 |
| A ≤ 0 | Aпр = 1|A| | -1010112; Aпр = 11010112 |
Для записи обратного кода цифры заменяют на противоположное значение, первую единицу от прямого кода оставляют без изменений:
| A > 0 | Aобр = 0A | 1010112; Aобр = 01010112 |
| A ≤ 0 | Aобр = 1 A | -1010112; Aобр = 10101002 |
Дополнительный код предполагает использование обратного кода, с той лишь разницей, что к отрицательному числу прибавляют единицу:
| A > 0 | Aдоп = 0A | 1010112; Aдоп = 01010112 |
| A ≤ 0 | Aдоп = 1 A + 1 | -1010112; Aдоп = 10101012 |
Применение двоичной системы в информатике
Двоичная система получила особое распространение в программировании цифровых устройств, так как она соответствует требованиям многих технических устройств, поддерживающих два состояния (есть ток, нет тока). Кроме того, является более простой и надежной для кодирования информации. Именно поэтому программный код большей части ЭВМ основан именно на двоичной системе счисления.











