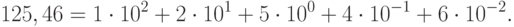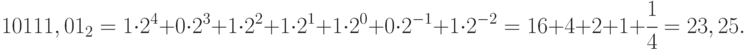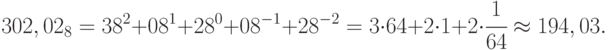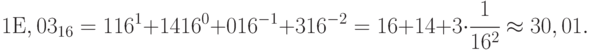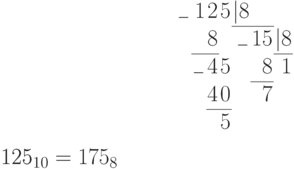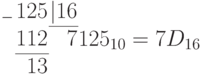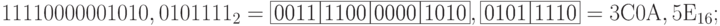Что такое двоичная арифметика
Двоичная арифметика
Категории Дискретная математика | Под редакцией сообщества: Математика
Содержание
↑Двоичная арифметика
Двоичная арифметика – краткое наименование системы арифметических операций (включающей сложение, вычитание, умножение, деление, иногда некоторые другие операции) над двоичными числами, т.е. целыми числами, представленными в двоичной позиционной системе; собирательное название схемных решений для выполнения арифметических операций над двоичными числами – сумматоров, умножителей, схем вычитания, деления и другие.
В последнее время почти вся техника, связанная с передачей и обработкой информации, стала цифровой. Цифровыми стали аудио и видеомагнитофоны, превратившись в DVD-плейеры и Айподы, телевизоры, фотоаппараты, а многие виды электронно-вычислительной техники и современные мобильные телефоны были цифровыми изначально. Это означает, что информация, циркулирующая в этих устройствах, представляется (или, как говорят, кодируется) в цифровом виде, т.е. как правило, в виде строк (или последовательностей), состоящих из нулей и единиц. Этим строкам можно сопоставить по некоторым правилам целые числа, для чего обычно используется двоичная позиционная система их записи.
Таким образом, с определенной точки зрения, все цифровые устройства генерируют потоки целых чисел, по некоторым правилам их преобразуют, обрабатывают, кодируют, декодируют и т.д., и передают другим цифровым устройствам. Область науки и техники, которая занимается изучением подобных процессов, называется цифровой обработкой сигналов (английская аббревиатура DSP – Digital Signal Processing).
Существенную роль в этом играют алгоритмические процедуры, выполняющие арифметические и логические операции с различными типами числовых данных. Проектированием подобных алгоритмов и устройств, их реализующих, занимается компьютерная арифметика. Ее математической основой является теория сложности так называемых булевых функций (более длинно именуемых функциями алгебры логики).
В большей своей части компьютерная арифметика является двоичной арифметикой. Этому есть две причины. Во-первых, алгоритмы арифметических операций двоичной арифметики (т.е. арифметики, использующей двоичную позиционную систему) очень просты и являются в определенном смысле простейшими среди подобных алгоритмов для всех позиционных числовых систем. Во-вторых, дискретные (не аналоговые) электронные схемы, как самые современные, так и использовавшиеся много лет назад, имеют в определенном смысле двоичную природу и легко описываются на языке алгебры логики. Алгебра логики применяется как для моделирования функционирования этих схем, так и для их проектирования (синтеза).
↑Схемная реализация булевых функций
Из функциональных элементов строятся схемы, реализующие булевы функции. Неформально говоря, схема из функциональных элементов может быть построена путем произвольного соединения выходов некоторых элементов с входами других элементов так, чтобы различные выходы не присоединялись к одному и тому же входу и не возникали ориентированные циклы из элементов. Пример схемы из функциональных элементов приведен на рисунке ниже. Под сложностью схемы понимается число входящих в нее функциональных элементов. Подробнее см. статью « Сложность булевых функций».
↑Двоичная позиционная система записи целых чисел
Главное достоинство двоичной системы (помимо естественности ее применения в электронной цифровой технике ) – исключительная простота алгоритмов арифметических операций в ней. Таблица умножения в двоичной системе совсем не требует запоминания: любое число, умноженное на нуль дает нуль, а умноженное на единицу равно самому себе. Правило деления сводится к двум равенствам 0/1 = 0, 1/1 =1, благодаря чему деление столбиком в двоичной системе делается проще, чем в десятичной, и по существу сводится к многократному вычитанию. Таблица сложения в двоичной системе чуть сложнее таблицы умножения (в отличие от десятичной системы), так как 1+1 = (10)2 и возникает перенос в следующий разряд.
Правило сложения двух битов в двоичной системе задается формулами x+y = 2v+u, v = x&y, u = xÅy. В силу симметрии для их проверки достаточно рассмотреть не четыре, а три случая: 0+0 = (00)2, 1+0=0+1= (01)2, 1+1 = (10)2. Схема, выполняющая это сложение, называется полусумматором (в англоязычной литературе: half adder) и обозначается обычно HA или FA2. Эта схема (в базисе
Схемы для арифметических операций над многоразрядными двоичными числами. Сложение двух n-разрядных двоичных чисел (xn,….,x1)2 и (yn,….,y1)2 как и в десятичной системе приводит к появлению переносов в следующий разряд, которые необходимо учитывать в вычислении. Эти переносы также равны нулю или единице (если перенос равен нулю, то в ручном вычислении он фактически не выполняется, но логическая схема обязана правильно работать и в этом случае, ведь она «не знает», какой перенос пришел из предыдущего разряда). Обозначим перенос из (i-1)-го разряда в следующий i-й разряд через wi (w1=0, потому что предыдущего разряда в этом случае просто нет). Тогда для вычисления zi (i-го бита результата) нужно сложить биты xi и yi и бит переноса wi. Это сложение выполняем по формулам
Схема сложения трехразрядных чисел приведена на следующем рисунке. Аналогичным образом выглядит и схема сложения n-разрядных чисел.
Сложность указанного n-разрядного сумматора равна 5n-3. Н.П.Редькин доказал, что сумматоров для n-разрядных чисел меньшей сложности в базисе
Глубина схемы – не менее важная характеристика схемы, чем ее сложность. Сложность логической схемы в значительной степени определяет площадь соответствующей реальной схемы, расположенной на кремниевом кристалле. Глубина же логической схемы в значительной мере определяет задержку реальной схемы, т.е. время, за которое сигнал проходит от входов схемы к ее выходам, другими словами, время, которое должно пройти после стабилизации каких-либо значений на входах схемы до того момента, когда на всех выходах схемы также стабилизируются определенные логические значения. Сложность схемы часто не имеет существенного значения, так как современные технологии позволяют разместить на кристалле очень большие схемы. А минимизация задержки схемы очень важна, так как задержка комбинационной части многотактной схемы определяет ее тактовую частоту – чем меньше задержка, тем выше частота.
Теоретически вычислить задержку реальной схемы очень сложно. Цепей элементов схемы, соединяющих ее входы с выходами (эти цепи также называют путями), обычно довольно много и задержка схемы определяется задержкой по самому плохому в определенном смысле пути, который называется критическим. Например, на схеме FA3 критический путь, вероятно, соединяет входы X или Y с выходом m. Задержка по любому пути определяется не только суммой задержек всех элементов, лежащих на этом пути (в приведенном примере она равна 3, если считать задержку каждого элемента единичной). Следует учитывать также задержку соединяющих эти элементы проводов. Задержка элемента зависит от того, между каким его входом и каким его выходом она измеряется, а также от электрических характеристик самого элемента и элементов непосредственно с ним связанных в рассматриваемой схеме, она зависит от температуры схемы и даже от того, какие логические значения подаются в рассматриваемый момент на входы этого элемента и изменяется ли (и в какую сторону) значение на его выходе. Тем не менее, хотя и не очень точно, задержку пути можно оценить как сумму задержек его элементов. Если задержки всех элементов равны, то эта величина определяется глубиной схемы. Разумеется, понятие глубины схемы можно расширить, допустив, что элементы базиса могут иметь произвольные неотрицательные задержки.
Глубина указанной выше схемы n-разрядного сумматора на первый взгляд равна 3n-2. Но внимательный анализ возможных критических путей показывает, что она на самом деле равна 2n-1. Все равно это очень много и построенная таким образом реальная схема будет иметь большую задержку. На практике используются схемы, имеющие одновременно малую сложность, не превосходящую Cn (где С – небольшая константа) и малую глубину, приблизительно равную 2log2 n. В.М. Храпченко в 1970 г. построил схему малой сложности и глубины, асимптотически равной log2n (т.е. равную (1+ e(n)) log2n, где e(n) стремится к нулю с ростом n). Он же недавно доказал, что глубина сумматора не может быть меньше log2n + log2n (log2 (log2n))). Поэтому построенная им схема имеет асимптотически минимальную глубину. Однако схема Храпченко превосходит обычные схемы только при n порядка тысячи. Тем не менее существует некоторая модификация его схемы с глубиной приблизительно равной logjn, где j = (Ö5+1)/2, и эта схема имеет глубину меньшую, чем стандартные схемы, уже начиная с n = 8. В 2008 г. М.И.Гринчук построил схему глубины не большей log2n+log2(log2n)+6, которая уже при малых n имеет меньшую глубину, чем все известные схемы.
Впоследствии были найдены схемы для деления с глубиной по порядку равной log2n, но их сложность оказалась велика. Американцы Рейф и Тейт построили схемы для деления глубины по порядку не превосходящей log2n log2(log2n) и одновременно сложности по порядку не превосходящей n log2n log2 log2n, однако и эти схемы, как и схемы Шенхаге-Штрассена и Фюрера пока не нашли практических применений, так как в действительности начинают превосходить используемые на практике схемы лишь при огромных значениях n.
↑Рекомендуемая литература
Эта статья еще не написана, но вы можете сделать это.
Двоичная арифметика
Арифметические действия в двоичной системе производятся по обычным для позиционных систем правилам, которые нам известны из десятичной арифметики, но при этом используются таблицы сложения и умножения двоичной системы:
Таблица сложения в двоичной системе очень проста. Надо только помнить, что прибавление нуля не меняет число, а один плюс один, будет два.
Таблица умножения ещё проще. Здесь нужно твёрдо знать, что любое число, умноженное на нуль, есть нуль и что умножение на единицу не меняет числа.
Сложение многозначных чисел производится точно так же, как и в десятичной системе, то есть поразрядно, начиная с младшего. Например:
Вычитание в двоичной системе выполняется по таким правилам:
Точки, поставленные над некоторыми разрядами уменьшаемого, показывают, что в двоичной системе единица помеченного разряда раздробляется на две единицы низшего разряда.
Умножение и деление двоичных чисел практически не отличается от умножения и деления чисел, записанных в десятичной системе счисления. Единственным отличием является то, что при умножении в столбик не приходится находить произведение первого множителя на значения последовательных разрядов второго множителя, так как значение этих разрядов 1 или 0. А при делении в столбик не нужно подбирать неполное делимое, так как учитывая специфику двоичных чисел, неполное делимое можно определить просто посмотрев на делимое.
Примеры. Выполнить умножение и деление:
Двоичная арифметика
Категории Дискретная математика | Под редакцией сообщества: Математика
Содержание
↑Двоичная арифметика
Двоичная арифметика – краткое наименование системы арифметических операций (включающей сложение, вычитание, умножение, деление, иногда некоторые другие операции) над двоичными числами, т.е. целыми числами, представленными в двоичной позиционной системе; собирательное название схемных решений для выполнения арифметических операций над двоичными числами – сумматоров, умножителей, схем вычитания, деления и другие.
В последнее время почти вся техника, связанная с передачей и обработкой информации, стала цифровой. Цифровыми стали аудио и видеомагнитофоны, превратившись в DVD-плейеры и Айподы, телевизоры, фотоаппараты, а многие виды электронно-вычислительной техники и современные мобильные телефоны были цифровыми изначально. Это означает, что информация, циркулирующая в этих устройствах, представляется (или, как говорят, кодируется) в цифровом виде, т.е. как правило, в виде строк (или последовательностей), состоящих из нулей и единиц. Этим строкам можно сопоставить по некоторым правилам целые числа, для чего обычно используется двоичная позиционная система их записи.
Таким образом, с определенной точки зрения, все цифровые устройства генерируют потоки целых чисел, по некоторым правилам их преобразуют, обрабатывают, кодируют, декодируют и т.д., и передают другим цифровым устройствам. Область науки и техники, которая занимается изучением подобных процессов, называется цифровой обработкой сигналов (английская аббревиатура DSP – Digital Signal Processing).
Существенную роль в этом играют алгоритмические процедуры, выполняющие арифметические и логические операции с различными типами числовых данных. Проектированием подобных алгоритмов и устройств, их реализующих, занимается компьютерная арифметика. Ее математической основой является теория сложности так называемых булевых функций (более длинно именуемых функциями алгебры логики).
В большей своей части компьютерная арифметика является двоичной арифметикой. Этому есть две причины. Во-первых, алгоритмы арифметических операций двоичной арифметики (т.е. арифметики, использующей двоичную позиционную систему) очень просты и являются в определенном смысле простейшими среди подобных алгоритмов для всех позиционных числовых систем. Во-вторых, дискретные (не аналоговые) электронные схемы, как самые современные, так и использовавшиеся много лет назад, имеют в определенном смысле двоичную природу и легко описываются на языке алгебры логики. Алгебра логики применяется как для моделирования функционирования этих схем, так и для их проектирования (синтеза).
↑Схемная реализация булевых функций
Из функциональных элементов строятся схемы, реализующие булевы функции. Неформально говоря, схема из функциональных элементов может быть построена путем произвольного соединения выходов некоторых элементов с входами других элементов так, чтобы различные выходы не присоединялись к одному и тому же входу и не возникали ориентированные циклы из элементов. Пример схемы из функциональных элементов приведен на рисунке ниже. Под сложностью схемы понимается число входящих в нее функциональных элементов. Подробнее см. статью « Сложность булевых функций».
↑Двоичная позиционная система записи целых чисел
Главное достоинство двоичной системы (помимо естественности ее применения в электронной цифровой технике ) – исключительная простота алгоритмов арифметических операций в ней. Таблица умножения в двоичной системе совсем не требует запоминания: любое число, умноженное на нуль дает нуль, а умноженное на единицу равно самому себе. Правило деления сводится к двум равенствам 0/1 = 0, 1/1 =1, благодаря чему деление столбиком в двоичной системе делается проще, чем в десятичной, и по существу сводится к многократному вычитанию. Таблица сложения в двоичной системе чуть сложнее таблицы умножения (в отличие от десятичной системы), так как 1+1 = (10)2 и возникает перенос в следующий разряд.
Правило сложения двух битов в двоичной системе задается формулами x+y = 2v+u, v = x&y, u = xÅy. В силу симметрии для их проверки достаточно рассмотреть не четыре, а три случая: 0+0 = (00)2, 1+0=0+1= (01)2, 1+1 = (10)2. Схема, выполняющая это сложение, называется полусумматором (в англоязычной литературе: half adder) и обозначается обычно HA или FA2. Эта схема (в базисе
Схемы для арифметических операций над многоразрядными двоичными числами. Сложение двух n-разрядных двоичных чисел (xn,….,x1)2 и (yn,….,y1)2 как и в десятичной системе приводит к появлению переносов в следующий разряд, которые необходимо учитывать в вычислении. Эти переносы также равны нулю или единице (если перенос равен нулю, то в ручном вычислении он фактически не выполняется, но логическая схема обязана правильно работать и в этом случае, ведь она «не знает», какой перенос пришел из предыдущего разряда). Обозначим перенос из (i-1)-го разряда в следующий i-й разряд через wi (w1=0, потому что предыдущего разряда в этом случае просто нет). Тогда для вычисления zi (i-го бита результата) нужно сложить биты xi и yi и бит переноса wi. Это сложение выполняем по формулам
Схема сложения трехразрядных чисел приведена на следующем рисунке. Аналогичным образом выглядит и схема сложения n-разрядных чисел.
Сложность указанного n-разрядного сумматора равна 5n-3. Н.П.Редькин доказал, что сумматоров для n-разрядных чисел меньшей сложности в базисе
Глубина схемы – не менее важная характеристика схемы, чем ее сложность. Сложность логической схемы в значительной степени определяет площадь соответствующей реальной схемы, расположенной на кремниевом кристалле. Глубина же логической схемы в значительной мере определяет задержку реальной схемы, т.е. время, за которое сигнал проходит от входов схемы к ее выходам, другими словами, время, которое должно пройти после стабилизации каких-либо значений на входах схемы до того момента, когда на всех выходах схемы также стабилизируются определенные логические значения. Сложность схемы часто не имеет существенного значения, так как современные технологии позволяют разместить на кристалле очень большие схемы. А минимизация задержки схемы очень важна, так как задержка комбинационной части многотактной схемы определяет ее тактовую частоту – чем меньше задержка, тем выше частота.
Теоретически вычислить задержку реальной схемы очень сложно. Цепей элементов схемы, соединяющих ее входы с выходами (эти цепи также называют путями), обычно довольно много и задержка схемы определяется задержкой по самому плохому в определенном смысле пути, который называется критическим. Например, на схеме FA3 критический путь, вероятно, соединяет входы X или Y с выходом m. Задержка по любому пути определяется не только суммой задержек всех элементов, лежащих на этом пути (в приведенном примере она равна 3, если считать задержку каждого элемента единичной). Следует учитывать также задержку соединяющих эти элементы проводов. Задержка элемента зависит от того, между каким его входом и каким его выходом она измеряется, а также от электрических характеристик самого элемента и элементов непосредственно с ним связанных в рассматриваемой схеме, она зависит от температуры схемы и даже от того, какие логические значения подаются в рассматриваемый момент на входы этого элемента и изменяется ли (и в какую сторону) значение на его выходе. Тем не менее, хотя и не очень точно, задержку пути можно оценить как сумму задержек его элементов. Если задержки всех элементов равны, то эта величина определяется глубиной схемы. Разумеется, понятие глубины схемы можно расширить, допустив, что элементы базиса могут иметь произвольные неотрицательные задержки.
Глубина указанной выше схемы n-разрядного сумматора на первый взгляд равна 3n-2. Но внимательный анализ возможных критических путей показывает, что она на самом деле равна 2n-1. Все равно это очень много и построенная таким образом реальная схема будет иметь большую задержку. На практике используются схемы, имеющие одновременно малую сложность, не превосходящую Cn (где С – небольшая константа) и малую глубину, приблизительно равную 2log2 n. В.М. Храпченко в 1970 г. построил схему малой сложности и глубины, асимптотически равной log2n (т.е. равную (1+ e(n)) log2n, где e(n) стремится к нулю с ростом n). Он же недавно доказал, что глубина сумматора не может быть меньше log2n + log2n (log2 (log2n))). Поэтому построенная им схема имеет асимптотически минимальную глубину. Однако схема Храпченко превосходит обычные схемы только при n порядка тысячи. Тем не менее существует некоторая модификация его схемы с глубиной приблизительно равной logjn, где j = (Ö5+1)/2, и эта схема имеет глубину меньшую, чем стандартные схемы, уже начиная с n = 8. В 2008 г. М.И.Гринчук построил схему глубины не большей log2n+log2(log2n)+6, которая уже при малых n имеет меньшую глубину, чем все известные схемы.
Впоследствии были найдены схемы для деления с глубиной по порядку равной log2n, но их сложность оказалась велика. Американцы Рейф и Тейт построили схемы для деления глубины по порядку не превосходящей log2n log2(log2n) и одновременно сложности по порядку не превосходящей n log2n log2 log2n, однако и эти схемы, как и схемы Шенхаге-Штрассена и Фюрера пока не нашли практических применений, так как в действительности начинают превосходить используемые на практике схемы лишь при огромных значениях n.
↑Рекомендуемая литература
Эта статья еще не написана, но вы можете сделать это.
Двоичные числа и двоичная арифметика
Принцип представления чисел в позиционных системах счисления
Позиционной называется система счисления, в которой вес разряда числа определяется его позицией в записи числа [1].
сотни десятки единицы десятые доли сотые доли
Аналогично любое число 
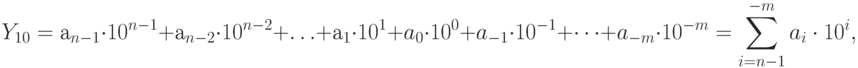 | ( 11.1) |
Для числа в системе счисления с основанием 
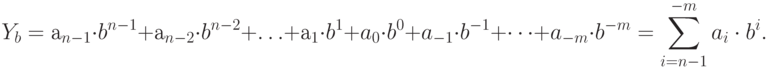 | ( 11.2) |
| Название системы счисления | Основание системы счисления | Знаки, использующиеся для записи чисел |
|---|---|---|
| Двоичная | 2 | 0, 1 |
| Троичная | 3 | 0, 1, 2 |
| Четверичная | 4 | 0, 1, 2, 3 |
| … | … | … |
| Восьмеричная | 8 | 0, 1, 2, 3, 4, 5, 6, 7 |
| … | … | … |
| Десятичная | 10 | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 |
| … | … | … |
| Шестнадцатеричная | 16 | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F |
| … | … | … |
Приведем примеры записи чисел в указанных системах и найдем их десятичные эквиваленты по формуле (11.2).
Для двоичного числа:
Для восьмеричного числа:
Для шестнадцатеричного числа:
Округление относится к дробной части числа, целая часть переводится точно. Особенностью перевода из шестнадцатеричного кода в десятичный код является то, что в качестве коэффициента 


Из рассмотренных примеров видно, что общая формула (11.2) может использоваться для перевода числа из системы счисления с любым основанием в десятичную.
Перевод чисел из одной системы счисления в другую
Перевод из десятичной системы в любую другую. Перевод целых чисел
Проверка перевода осуществляется по формуле (11.2), так, как это показано ниже на примерах.
Пример. Перевести десятичное число 125 в двоичную, восьмеричную и шестнадцатеричную системы счисления. Проверить результаты по формуле (П11.2).
В рассмотренном примере при переводе вместо коэффициента 
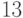
Перевод из двоичной системы в шестнадцатеричную (восьмеричную)
Как уже было сказано выше, шестнадцатеричный и восьмеричный коды используются для более компактной и удобной записи двоичных чисел. Так, программирование в машинных кодах осуществляется в большинстве случаев в шестнадцатеричном коде. Правила перевода для шестнадцатеричной и восьмеричной системы структурно одинаковы, отличия для восьмеричной системы отображаются в скобках.
Двоичная запись числа делится на группы по четыре ( три ) двоичных знака влево и вправо от запятой, отделяющей целые и дробные части Неполные крайние группы (если они есть) дополняются нулями до четырех ( трех ) знаков. Каждая группа заменяется одним шестнадцатеричным ( восьмеричным ) знаком в соответствии с кодом группы (табл. 11.2).
| Двоичная группа | Шестнадцатеричный знак | Десятичный эквивалент | Двоичная группа | Восьмеричный знак |
|---|---|---|---|---|
| 0000 | 0 | 0 | 000 | 0 |
| 0001 | 1 | 1 | 001 | 1 |
| 0010 | 2 | 2 | 010 | 2 |
| 0011 | 3 | 3 | 011 | 3 |
| 0100 | 4 | 4 | 100 | 4 |
| 0101 | 5 | 5 | 101 | 5 |
| 0110 | 6 | 6 | 110 | 6 |
| 0111 | 7 | 7 | 111 | 7 |
| 1000 | 8 | 8 | ||
| 1001 | 9 | 9 | ||
| 1010 | A | 10 | ||
| 1011 | B | 11 | ||
| 1100 | C | 12 | ||
| 1101 | D | 13 | ||
| 1110 | E | 14 | ||
| 1111 | F | 15 |
Перевод из шестнадцатеричной (восьмеричной) системы в двоичную
Каждая цифра (без всяких сокращений!) шестнадцатеричного ( восьмеричного ) числа заменяется одной двоичной группой из четырех ( трех ) двоичных знаков (табл. 11.2).
Как показано в примерах, крайние нули слева и справа при желании можно не писать, но такое сокращение делается уже после перевода в двоичную систему.