I. Механика

Тестирование онлайн

Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.

Угловая скорость

Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.

Период и частота

Частота и период взаимосвязаны соотношением

Связь с угловой скоростью

Линейная скорость

Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.

Центростремительное ускорение

При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.

Используя предыдущие формулы, можно вывести следующие соотношения

Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.

Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.

Вращение Земли

Земля участвует в двух основных вращательных движениях: суточном (вокруг своей оси) и орбитальном (вокруг Солнца). Период вращения Земли вокруг Солнца составляет 1 год или 365 суток. Вокруг своей оси Земля вращается с запада на восток, период этого вращения составляет 1 сутки или 24 часа. Широтой называется угол между плоскостью экватора и направлением из центра Земли на точку ее поверхности.

Связь со вторым законом Ньютона

Согласно второму закону Ньютона причиной любого ускорения является сила. Если движущееся тело испытывает центростремительное ускорение, то природа сил, действием которых вызвано это ускорение, может быть различной. Например, если тело движется по окружности на привязанной к нему веревке, то действующей силой является сила упругости.

Если тело, лежащее на диске, вращается вместе с диском вокруг его оси, то такой силой является сила трения. Если сила прекратит свое действие, то далее тело будет двигаться по прямой

Как вывести формулу центростремительного ускорения

Разница векторов есть . Так как , получим

Движение по циклоиде*

В системе отсчета, связанной с колесом, точка равномерно вращается по окружности радиуса R со скоростью , которая изменяется только по направлению. Центростремительное ускорение точки направлено по радиусу к центру окружности.

Теперь перейдем в неподвижную систему, связанную с землей. Полное ускорение точки А останется прежним и по модулю, и по направлению, так как при переходе от одной инерциальной системы отсчета к другой ускорение не меняется. С точки зрения неподвижного наблюдателя траектория точки А — уже не окружность, а более сложная кривая (циклоида), вдоль которой точка движется неравномерно.

Мгновенная скорость определяется по формуле

Источник

Движение по окружности

Зная угловое перемещение, можно вычислить длину дуги окружности (путь), которую прошло тело.

Угловая скорость

Определение. Угловая скорость

Существует связь между угловой и линейной скоростями тела при движении по окружности. Формула для нахождения угловой скорости:

Нормальное ускорение

При равномерном движении по окружности, скорости v и ω остаются неизменными. Меняется только направление вектора линейной скорости.

При этом равномерное движение по окружности на тело действует центростремительное, или нормальное ускорение, направленное по радиусу окружности к ее центру.

Модуль центростремительного ускорения можно вычислить по формуле:

Докажем эти соотношения.

В точках А и В вектор скорости направлен по касательной к окружности, при этом модули скоростей в обеих точках одинаковы.

По определению ускорения:

Взглянем на рисунок:

R v ∆ t = v ∆ v или ∆ v ∆ t = v 2 R

При равномерном движении по окружности модуль ускорения остается постоянным, а направление вектора изменяется со временем, сохраняя ориентацию на центр окружности. Именно поэтому это ускорение называется центростремительным: вектор в любой момент времени направлен к центру окружности.

Запись центростремительного ускорения в векторной форме выглядит следующим образом:

Тангенциальное ускорение

Рассмотрим случай, когда тело движется по окружности неравномерно. Введем понятие тангенциального (касательного) ускорения. Его направление совпадает с направлением линейной скорости тела и в каждой точке окружности направлено по касательной к ней.

a τ = ∆ v τ ∆ t ; ∆ t → 0

Направление полного ускорения определяется векторной суммой нормального и тангенциального ускорений.

Если движение равномерное, величины v x и v y а также соответствующие координаты будут изменяться во времени по гармоническому закону с периодом T = 2 π R v = 2 π ω

Источник

Движение по окружности

Наряду с движением вдоль прямой в школьной физике рассматривают движение по окружности. Для него, по аналогии с прямолинейным движением, вводятся понятия пройденного пути, скорости движения и ускорения.

В физике выделяют несколько видов движения тел. Движение по окружности – это один из случаев движения вдоль кривой линии — криволинейного движения.

Сравним понятия пройденного пути, скорости и ускорения для прямолинейного движения и движения по окружности.

Угловой путь

Для начала, вспомним, что линейное перемещение – это разница между конечным и начальным положением точки на оси (рис. 1).

Рассмотрим теперь колесо (рис. 2). На горизонтальной линии, проходящей через диаметр колеса, справа отметим красную точку, от которой мы начнем отсчитывать углы. Условимся считать, что возле этой точки находится нулевой угол.

На ободе колеса выберем точку, например — ниппель. Сначала ниппель находился в точке 1. Точка 1 сдвинута на угол \(\gamma_<1>\) относительно начала отсчета.

Будем вращать колесо в направлении, обозначенном синей стрелкой. Повернем колесо на некоторый угол, так, чтобы к концу движения ниппель переместился в точку, обозначенную цифрой 2 на рисунке. Эта точка смещена на угол \(\gamma_<2>\) по отношению к началу отсчета.

По аналогии с поступательным движением, угловой путь, который прошел ниппель — это разница (разность) угловых положений точек 1 и 2.

\(\varphi \left( \text<рад>\right)\) – угловой путь измеряется в радианах.

Угловой путь – это угол, на который повернулся ниппель, по отношению к его начальному положению.

Угловая скорость — куда она направлена

Если тело двигалось равномерно (с неизменной скоростью), то линейную скорость можно определить по формуле

\(v \left( \frac<\text<м>> \right)\) — линейная скорость – это путь, деленный на время, поэтому она имеет размерность метров деленных на секунду.

Аналогично линейному случаю, если угловой путь поделить на время движения, получим угловую скорость.

\(\omega \left( \frac<\text<рад>> \right)\) – угловая скорость – это угловой путь, деленный на время, поэтому она имеет размерность радиан деленных на секунду.

Угловая скорость \( \omega \), так же, как и линейная скорость, является вектором. Но в отличии от линейной скорости его направление можно определить по правилу буравчика (правого винта).

Примечание: Направление вектора угловой скорости \( \vec <\omega>\) можно определить по правилу буравчика (правого винта)!

На рисунке 3 окружность располагается в горизонтальной плоскости, а вектор \( \vec<\omega >\) направлен вдоль вертикальной оси вращения. Направление вращения указано синей стрелкой.

При движении по окружности вектор линейной скорости \(\vec\) изменяет свое направление. Но в каждой точке окружности вектор \(\vec\) направлен по касательной к окружности, т. е. перпендикулярно радиусу.

Примечание: Касательная и радиус перпендикулярны, это известно из геометрии.

Если точка начнет вращаться в противоположную сторону, то векторы линейной и угловой скорости развернутся противоположно направлениям, указанным на рисунке 3.

Связь между линейной и угловой скоростью

Угловая и линейная скорость связаны математически. Линейная скорость – это векторное произведение вектора угловой скорости и вектора радиуса окружности.

Примечание: Радиус окружности – это вектор, он направлен от центра окружности к ее внешней границе.

Скалярный вид записи связи скоростей:

\(\omega \left( \frac<\text<рад>> \right)\) – угловая скорость;

\(v \left( \frac<\text<м>> \right)\) — линейная скорость;

\(R \left( \text<м>\right)\) – радиус окружности.

Частота и период

Вращательное движение описывают с помощью таких характеристик, как частота и период.

Период обращения – это время одного полного оборота. В системе СИ период измеряют в секундах.

\( T \left(c \right)\) – время, за которое тело совершило полный оборот – период. Время – это скалярная величина.

Частота отвечает на вопрос: «Сколько полных оборотов совершило тело за одну секунду?».

\( \displaystyle \nu\left( \frac<1> \right)\) – частота оборотов, скаляр.

Вместо записи \( \displaystyle \left( \frac<1> \right)\) иногда используют \(\displaystyle \left( c^ <-1>\right)\), или \( \left( \text <Гц>\right)\) – Герц. Это фамилия Генриха Герца, знаменитого физика.

\[\displaystyle 1 \text <Гц>= \frac<1> = c^ <-1>\]

Частота и период связаны обратной пропорциональностью:

Количество оборотов

Двигаясь по окружности достаточное время, тело может пройти не один оборот. Зная угловой путь \(\varphi \) мы можем вычислить количество N оборотов.

\( N \) – количество оборотов, скаляр. Обороты считают поштучно.

Связь между угловой скоростью и частотой

Разделим обе части уравнения на время t, в течение которого тело вращалось

Левая часть уравнения – это угловая скорость.

А дробь в правой части – это частота

Таким образом, мы получили связь между угловой скоростью и частотой

Примечание: Решая задачи на равноускоренное движение по окружности, удобно переходить от частоты к угловой скорости. Тогда можно будет применять аналогию с формулами для равноускоренного движения по прямой.

Источник

Что такое движение по окружности в физике

4.1. Движение по окружности с постоянной скоростью.

Движение по окружности — простейший вид криволинейного движения.

4.1.1. Криволинейное движение — движение, траекторий которого является кривая линия.

Для движения по окружности с постоянной скоростью:

1) траектория движения — окружность;

2) вектор скорости направлен по касательной к окружности;

3) вектор скорости постоянно меняет свое направление;

4) за изменение направления скорости отвечает ускорение, называемое центростремительным (или нормальным) ускорением;

5) центростремительное ускорение меняет только направление вектора скорости, при этом модуль скорости остается неизменным;

6) центростремительное ускорение направлено к центру окружности, по которой происходит движение (центростремительное ускорение всегда перпендикулярно вектору скорости).

4.1.2. Период (T) — время одного полного оборота по окружности.

Это величина постоянная, так как длина окружности постоянная и скорость движения постоянна

4.1.3 Частота — число полных оборотов за 1 с.

По сути, частота отвечает на вопрос: как быстро вращается тело?

4.1.4. Линейная скорость — показывает, какой путь проходит тело за 1 с (это та же самая скорость, о которой говорилось в предыдущих темах)

где R — радиус окружности.

4.1.5. Угловая скорость показывает, на какой угол поворачивается тело за 1 с.

где — угол, на который повернулось тело за время

4.1.6. Центростремительное ускорение

Напомним, что центростремительное ускорение отвечает только за поворот вектора скорости. При этом, так как скорость постоянная величина, то значение ускорения тоже постоянно.

4.1.7. Закон изменения угла поворота

Это полный аналог закона движения при постоянной скорости :

Роль координаты x играет угол роль начальной координаты играет скорость — угловая скорость И с формулой следует работать так же, как ранее работали с формулой закона равномерного движения.

4.2. Движение по окружности с постоянным ускорением.

4.2.1. Тангенциальное ускорение

Центростремительное ускорение отвечает за изменение направления вектора скорости, но если еще меняется и модуль скорости, то необходимо ввести величину отвечающую за это — тангенциальное ускорение

Из вида формулы ясно, что — это обычное ускорение, о котором говорилось раньше. Если то справедливы формулы равноускоренного движения:

где S — путь, который проходит тело по окружности.

Итак, еще раз подчеркнем, отвечает за изменение модуля скорости.

4.2.2. Угловое ускорение

Мы ввели аналог скорости для движения по окружности — угловая скорость. Естественно будет ввести и аналог ускорения — угловое ускорение

Угловое ускорение связано с тангенциальным ускорением:

Из формулы видно, что если тангенциальное ускорение постоянно, то и угловое ускорение будет постоянно. Тогда можем записать:

Формула является полным аналогом закона равнопеременного движения, поэтому работать с этой формулой мы уже умеем.

4.2.3. Полное ускорение

Центростремительное (или нормальное) и тангенциальное ускорения не являются самостоятельными. На самом деле, это проекции полного ускорения на нормальную (направлена по радиусу окружности, то есть перпендикулярно скорости) и тангенциальную (направлена по касательной к окружности в сторону, куда направлен вектор скорости) оси. Поэтому

Нормальная и тангенциальные оси всегда перпендикулярны, следовательно, абсолютно всегда модуль полного ускорения можно найти по формуле:

4.4. Движение по криволинейной траектории.

Движение по окружности является частным видом криволинейного движения. В общем случае, когда траектория представляет собой произвольную кривую (см. рис.), всю траекторию можно разбить на участки: AB и DE — прямолинейные участки, для которых справедливы все формулы движения по прямой; а для каждой участка, который нельзя рассмотреть как прямую, строим касательную окружность (окружность, которая касается траектории только в этой точке) — в точках C и D. Радиус касательной окружности называется радиусом кривизны. В каждой точке траектории радиус кривизны имеет свое значение.

Формула для нахождения радиуса кривизны :

где — нормальное ускорение в данной точке (проекция полного ускорения на ось, перпендикулярную вектору скорости).

Источник

Учебник. Движение по окружности

Движение тела по окружности является частным случаем криволинейного движения. Наряду с вектором перемещения Δ s → удобно рассматривать угловое перемещение Δφ (или угол поворота), измеряемое в радианах (рис. 1.6.1). Длина дуги связана с углом поворота соотношением Δl = R Δφ.

При малых углах поворота Δl ≈ Δs.

Линейное Δ s → и угловое Δφ перемещения при движении тела по окружности

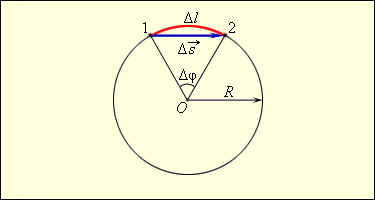
Угловая скорость измеряется в рад/с.

Связь между модулем линейной скорости υ и угловой скоростью ω: υ = ωR.

Векторы скоростей υ → A и υ → B в точках A и B направлены по касательным к окружности в этих точках. Модули скоростей одинаковы υ_A = υ_B = υ.

Центростремительное ускорение тела a → n при равномерном движении по окружности

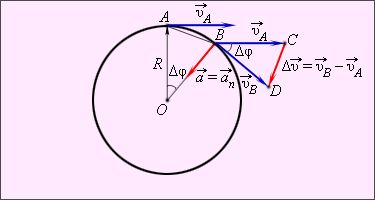
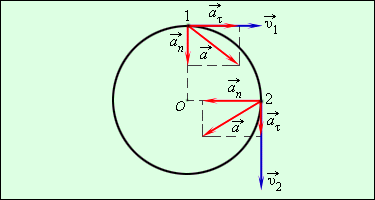
При изменении положения тела на окружности изменяется направление на центр окружности. При равномерном движении тела по окружности модуль ускорения остается неизменным, но направление вектора ускорения изменяется со временем. Вектор ускорения в любой точке окружности направлен к ее центру. Поэтому ускорение при равномерном движении тела по окружности называется центростремительным.

Равномерное движение по окружности

В этой формуле Δυ_τ = υ₂ – υ₁ – изменение модуля скорости за промежуток времени Δt.

Направление вектора полного ускорения a → = a → n + a → τ определяется в каждой точке круговой траектории величинами нормального и касательного ускорений (рис. 1.6.3).

Составляющие ускорения a → n и a → τ при неравномерном движении тела по окружности

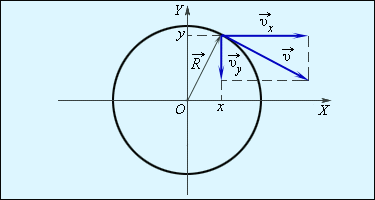
Движение тела по окружности можно описывать с помощью двух координат x и y (плоское движение). Скорость тела в каждый момент можно разложить на две составляющие υ_x и υ_y (рис. 1.6.4).

Разложение вектора скорости υ → по координатным осям

Источник