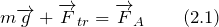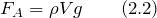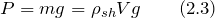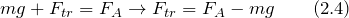Что такое движение по инерции привести примеры
ИНЕРЦИЯ И МОМЕНТ ИНЕРЦИИ: базовые сведения
История понятия «инерция»
До эпохи Возрождения, в Средние века, в западной философии общепринятой была аристотелевская теория движения. Ученик Платона, древнегреческий философ Аристотель (384 – 322 гг. до н. э.) утверждал, что в отсутствии внешней силы все объекты остановятся, и что движущиеся объекты продолжают двигаться только до тех пор, пока есть побуждающая к движению сила.
Принцип движения по инерции, который возник у Аристотеля для «движений в пустоте», гласил, что объект имеет тенденцию сопротивляться изменению движения.
Окончательно от аристотелевской теории отказались в ходе ряда открытий, предшествовавших научной революции XVII века.
Термин «инерция», от латинского слова «безделье» или «лень» (лат. inertia), был впервые использован немецким математиком и астрономом Иоганном Кеплером (1571 – 1630 гг.) в его книге «Epitome Astronomiae Copernicanae», которая была опубликована в трех частях в 1617–1621 гг. Но Кеплер определял инерцию только как сопротивление движению, основываясь на старом предположении, что покой – это естественной состояние вещей, которое не нужно объяснять и к которому стремятся тела.
Покой и движение объединил единым принципом современник Кеплера Галилео Галилей (1564 — 1642) — итальянский физик, механик, астроном, философ и математик. Он первый, кто направил зрительную трубу в небо, превратив её в телескоп. В 1609 году он создал свой первый телескоп с трёхкратным увеличением. Галилео Галилей писал, что «если устранить все внешние препятствия, то тяжелое тело на сферической поверхности, концентрической Земле, будет поддерживать себя в том состоянии, в котором оно находилось; если его поместить в движение к западу (например), то оно будет поддерживать себя в этом движении».
Чтобы оспорить идею Аристотеля о естественности состояния покоя, Галилей проводил один из таких мысленных экспериментов. Если исключить силу трения, то шар, катящийся по склону оврага (холма), взлетит до той же высоты на противоположной стороне. Если второй склон постепенно наклонять, шар будет катиться все дальше и дальше и в горизонтальном положении склона будет катиться бесконечно долго.
Галилей сделал вывод, что «Тело, движущееся по ровной поверхности, будет продолжать движение в том же направлении с постоянной скоростью, если движение не будет нарушено».
Позднее, мысли Галилея будут уточнены и систематизированы Исааком Ньютоном. Исаак Ньютон (1642 – 1727) — английский физик, математик, механик и астроном, основатель классической физики. В своем труде «Математические начала натуральной философии» (Philosophiae Naturalis Principia Mathematica), впервые опубликованном в 1687 году, он изложил закон всемирного тяготения и три закона динамики.
Явление инерции, изначально сформулированное Галилеем, вошло в первый закон Ньютона.
Оговоримся, что согласно определению, законы Ньютона справедливы только для систем отсчета (система отсчета – это тело отсчета со связанной с ним системой координат, относительно которого можно вычислять положение тел, и система измерения времени, т.е. некоторые часы), которые принято называть инерциальными. Инерциальная система отсчета – это такая система, в которой ускорение тел зависит только от приложенных сил, а не свойством самой системы отсчета (наблюдателя) перемещаться с ускорением.
Посмотрим на второй закон Ньютона.
Чаще его записывают в виде:
так как в инерциальной системе отсчета сила является причиной ускорения тела.
Как видно из второй формулы, для тела неизменной массы ускорение тела (скорость изменения его скорости) прямо пропорционально силе, приложенной к телу (чем сильнее толкаем, тем быстрее тело разгоняется) и обратно пропорционально его массе (чем тяжелее тело, тем сложнее его разгонять).
Представим, что тело движется в вакууме и на него не действуют никакие силы (F=0). Значит и скорость его меняться не будет (a=0).
Инерция (лат. inertia — покой, постоянство, неизменность) – природное явление сохранения равномерного прямолинейного движения или состояния покоя любого тела, пока на него не действуют внешние силы или если действие сил скомпенсировано.
Инертность – свойство конкретного тела оставаться в покое или равномерно прямолинейно двигаться. От инертности зависит ускорение тела при приложении к нему внешних сил. Мерой количественного измерения инертности тела в прямолинейном движении является его масса. Больше масса – больше инертность тела, т.е. тем сложнее придать ему ускорение (разогнать или остановить).
Из-за большей чем у легковушки массы у грузовика инертность выше. Соответственно, и тормозной путь у него будет больше – нужно приложить большую силу, чтоб его остановить (хотя, можно поставить очень мощные тормоза). Говорить, что у грузовика больше инерция – некорректно.
Мерой инертности тела в прямолинейном движении выступает его масса. Больше масса – больше инертность тела.
Инерция, кинетическая энергия, работа
Приведем другой пример. Представь тяжелоатлета… Даже двух, которые решили поставить мировой рекорд и сдвинуть самолет. Им придется приложить немало сил, чтобы вначале разогнать самолет от нуля до некоторой скорости, а потом поддерживать эту скорость, преодолевая силу трения, направленную назад. Конечно, проще сдвинуть с места (преодолеть инерцию покоя) и разогнать до большой скорости тело меньшей массы, например, футбольный мяч. Инертность самолета во много раз больше инертности футбольного мяча.
А к какому трюку прибегает фокусник, чтобы в случае со скатертью все предметы остались на столе? Правильно, нужно выдернуть скатерть за наименьшее время. Чем меньше время, тем меньше энергии перейдет с силой трения на предметы и они просто не успеют разогнаться.
Энергия движущегося тела называется кинетической энергией и измеряется в Джоулях. Если тело неподвижно, кинетическая энергия равна нулю.
Чтобы разогнать тело массой m до нужной скорости V из состояния покоя (например, самолет), нужно выполнить работу, равную кинетической энергии разогнанного тела (без учета разных потерь):
Работа по изменению кинетической энергии тела совершается за счет приложения к нему некоторой силы – силы тяжести, силы трения, силы воздействия на него другого тела (тяжелоатлета-силача, дующего ветра, реактивной тяги ракетного двигателя и пр.).
Пусть силач разогнал до 0.1 м/с (10 сантиметров в секунду) легковую машину массой 1200 кг и самолет Ил-76 массой 88 500 кг в космосе (не будем учитывать силу трения). Тогда для преодоления инерции этих тел ему пришлось сжечь мышечной энергии на 6 Дж и 442,5 Дж соответсвенно. Т.е. на преодоление инерции покоя у самолета у спортсмена уйдет в 74 раза больше энергии, чем на автомобиль.
Чтобы остановить тело массой m, движущееся со скоростью V, нужно совершить обратную работу, равную отрицательному значению кинетической энергии этого тела:
Т.е. чем больше скорость тела и его масса, тем больше энергии на преодоление инерции движения надо затратить.
Если выключить мотор, машина под действием силы трения ее движущихся частей друг о друга, силы трения о воздух корпуса и силы трения колес об асфальт остановится сама. Но остановить машину можно и быстрее, увеличив силу трения с помощью тормозных дисков, т.е. выжав педаль тормоза.
При равной скорости масса грузовика намного больше, а значит больше его кинетическая энергия. Двигаясь накатом грузовик остановится дальше, чем легковой автомобиль – его инертность выше. Кстати, можно ли остановить грузовик быстрее легкового автомобиля и при каких условиях?
Момент инерции
Инерция проявляется не только для прямолинейного движения, но и при вращении тел. В двигателе есть специальное устройство – маховик (на рисунке справа маховик покрашен темно-серым цветом и имеет зубчики). Инерция его вращения помогает работать двигателю нормально. Энергия расширяющихся газов при воспламенении топлива толкает поршень вниз, а затем ему нужно идти вверх, выталкивая продукты сгорания. Без маховика поршень не смог бы провернуть коленвал без рывков. Двигатель без маховика заглохнет.
Ну а со спинерами и волчками знакомы многие.
Вот только в приведенных примерах форма тела не меняется. А изменится ли инертность тела при изменении его формы?

Многие могут вспомнить фигурное катание. Масса тела фигуриста за выступление не меняется. Но его скорость вращения мгновенно увеличивается, стоит прижать руки и ноги, и вытянуться в струнку. Т.е. при уменьшении радиуса тела скорость вращения увеличивается. Т.е. инертность тела должна уменьшиться? Давайте разбираться.
Вернемся к формулам. Скорость вращающегося тела описывается как произведение угловой скорости (омега) на радиус:

При этом кинетическая энергия вращающегося тела примет вид:
Синим цветом выделено произведение массы тела на радиус в квадрате. Эта величина называется моментом инерции вращающегося тела и обозначается латинской буквой I (и).
Мерой инертности вращающего тела выступает момент инерции, который зависит от массы тела и расстояния этой массы от центра вращения.
Представим, что девочка не только вращает груз над собой, но и идет. Тогда полная кинетическая энергия девочки с грузом примет вид:
Первая часть описывает кинетическую энергию двигающейся прямолинейно с некоторой скоростью девочки с грузом, а вторая – кинетическую энергию вращающегося груза. Полная кинетическая энергия — это сумма энергии прямолинейно движущегося тела и энергии вращающегося тела. Точно так же кинетическая энергия будет рассчитываться для движущегося по столу раскрученного волчка или съезжающего с наклонной плоскости цилиндра.
Так как вращающееся тело может иметь форму, отличную от точки или маленького шарика, то и формула момента инерции для более точных расчетов может принимать разный вид.
Пример.
Цилиндры одинаковой массы (m1 = m2), но разного радиуса (r1 
В верхней точке кинетическая энергия обоих цилиндров будет равна нулю, так как скорость равна нулю. Потенциальная энергия будет одинаковой и максимальной.
При скатывании цилиндров по закону сохранения энергии потенциальная энергия переходит в кинетическую и в самой нижней точке будет равна нулю, так как высота равна нулю. А кинетическая энергия в нижней точке будет складываться из поступательной кинетической энергии и кинетической энергии вращающегося тела и у обоих тел также будет одинаковой, так как их потенциальные энергии были равны.
Но так как радиус первого тела меньше второго, то и момент инерции первого тела меньше второго и будет справедливо:
Тогда для кинетической энергии поступательного движения будет справедливо отношение:
Следовательно, скорость первого цилиндра должна быть выше скорости второго, и он скатится быстрее. Так как мерой инертности вращающегося тела является момент инерции, то первое тело с меньшим радиусом и меньшим моментом инерции будет обладать меньшей инертностью, чем второе. Разогнаться под действием каких-либо сил (силы тяжести) такому телу проще.
Вопросы
1. Посмотри на картинку с формулами для расчета момента инерции для тел разной формы. Как ты думаешь, какая формула лучше подходит для расчёта момента инерции маховика автомобиля. Варианты ответа: a, b, c, d, e, f, g, h, или i

2. Два волчка одинаковой массы раскрутили до одинаковой угловой скорости, но диаметр первого волчка меньше диаметра второго. Какой из них упадет раньше?
3. На рисунке показаны три варианта конструкции. Какой вариант машинки имеет наименьшую инертность, а какой максимальную? Почему?
Движение по инерции
Причиной изменения скорости движения тел, то есть возникновения ускорения, в механике считают их взаимодействие. Ускорение тела в некоторый момент времени определено положением тел и движением окружающих тел.
Долгое время, следуя Аристотелю, считалось, что для того, чтобы тело двигалось, пусть даже с постоянной скоростью, оно нуждается во внешнем воздействии. Если внешнего действия на тело нет, то тело находится в состоянии покоя. Только Галилей и позднее Ньютон показали, что движение тела с постоянной скоростью эквивалентно состоянию покоя тела. Для того чтобы тело находилось в покое или равномерном и прямолинейном движении на тело не должны действовать силы или их действие должно взаимно компенсироваться.
Движение по инерции
Всякое тело, которое было выведено из состояния покоя, после прекращения действия на него со стороны других тел, продолжает перемещаться по инерции.
На Земле такое движение практически невозможно. Представить движение по инерции можно только в идеальных условиях. Рассмотрим, например, скольжение тела по горизонтальной поверхности. Если поверхность тела гладкая и скользит оно по льду, то тело будет изменять свою скорость медленно. Можно представить, что идеально гладкое тело по идеально гладкой поверхности может двигаться с постоянной скоростью бесконечно долго. Иная ситуация сложится, если заставить скользить тоже самое тело по шероховатой поверхности. Оно быстро уменьшит свою скорость до нуля.
Инерциальные системы отсчета
Однако следует учитывать, что движение всегда относительно. В произвольной системе отсчета изменение скорости тела может произойти без того, чтобы на него оказали воздействие другие тела. Системы отсчета, в которых тело сохраняет состояние покоя или движется равномерно и прямолинейно, если на него не оказывают действие другие тела, называют инерциальными. Инерциальных систем бесконечно много, так как любая система отсчета, движущаяся равномерно и прямолинейно относительно инерциальной системы отсчета является в свою очередь инерциальной.
Получается, что понятие инерциальной системы отсчета связано с представлением о свободном теле. Считают, что если тело удалено от других тел достаточно далеко, то оно не испытывает взаимодействия с другими телами и является свободным. На практике условия свободного перемещения выполняются с большей или меньшей погрешностью. Эмпирически невозможно доказать существование инерциальных систем отсчета. Систем отсчета, связанную Землей (геоцентрическую систему), можно считать инерциальной лишь в некотором приближении, так как Земля вращается вокруг Солнца и собственной оси. С гораздо большей степенью точности инерциальной можно считать систему, связанную с Солнцем и звездами. Такая система называется гелиоцентрической.
Первый закон Ньютона
Существуют такие системы отсчета, в которых тело движется с постоянной скоростью или находится в покое, если на него не действуют другие тела или их действие взаимно скомпенсировано. Постулирование существования инерциальных систем отсчета – содержание первого закона Ньютона.
Примеры решения задач
| Задание | Для того чтобы экспериментально показать, что избранная система отсчета является инерциальной следует иметь свободное тело. Как можно установить, что на избранное тело не действуют другие тела? |
| Решение | Все известные на настоящий момент взаимодействия тел в макромире убывают с ростом расстояния между телами. Но нельзя быть абсолютно уверенным в отсутствии взаимодействия, если рассматриваемое тело не касается других тел или находится от них в удалении. Так, силы гравитации и электромагнитные силы играют существенную роль на относительно больших расстояниях между телами. Следовательно, установить факт отсутствия взаимодействия на основе удаления в пространстве можно только приближенно, с то или иной требуемой точностью. Говорят, что в этом смысле не существует решающего эксперимента, который можно было бы считать доказательством первого закона Ньютона. |
| Задание | Каково отношение силы трения шарика о жидкость к весу шарика (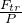 ), если он всплывает с постоянной скоростью. При этом известно отношение плотности жидкости ( ), если он всплывает с постоянной скоростью. При этом известно отношение плотности жидкости (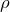 ) к плотности материала шарика ( ) к плотности материала шарика (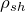 ): ( ): (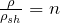 ). ). |
| Решение | Сделаем рисунок. |
По условию задачи шарик движется с постоянной скоростью, следовательно, из первого закона Ньютона следует, что силы, действующие на него, взаимно компенсируют друг друга.
На шарик действуют: сила тяжести: 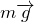
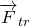
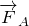
Силу Архимеда определим как:
Вес шарика у нас будет равен по модулю силе тяжести:
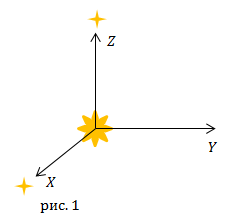
В проекции на ось Y (рис.1) уравнения (2.1) имеем:
Найдем, используя (2.4), (2.2) и (2.3) отношение 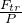
Физика поля
Беседы о сущности Физики поля
September 2021
| S | M | T | W | T | F | S |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 |
Беседа 2. Закон инерции
Коллега, ранее Вы говорили, что прямолинейное и одновременно равномерное движение невозможно. Но, разве это не движение по инерции?
Мой друг, инерция (от лат. inertia – бездействие) проявляется в том, что тело сохраняет неизменным состояние своего движения или покоя, когда действующие на тело силы отсутствуют или взаимно уравновешиваются. Такое движение мы можем называть инерционным.
Наблюдения действительно показывали, что тело останавливалось при прекращении действия толкающей его силы. Однако, при этом, не учитывалось противодействие естественных внешних сил (сил трения, сопротивления воздуха и т.п.).
Коллега, так вот Вам и упоминание о равномерном прямолинейном движении.
Именно в этом и заключается принципиальная ошибка. Ведь Галилей говорил о горизонтальной плоскости, а математики (Декарт, 1596–1650 и Ньютон, 1643–1727) посчитали, что прямая линия совпадает с такой плоскостью. Однако, если горизонтальную плоскость Галилея неограниченно продлить во все стороны, то получим обычную сферу с радиусом земного шара. Тогда, о каком прямолинейном движении здесь может идти речь?
Мы все существуем в силовом поле, которое для небольшого пространства (скажем, лаборатории) можно считать однородным (силы тяжести не зависят от координат и их векторы «параллельны» друг другу). В этом случае прямая и горизонтальная линии могут совпадать, ибо горизонтальный пол лаборатории нам кажется «идеально» плоским, а противоположные стены – «строго» параллельными. Здесь условия для движения по Галилею и Ньютону практически аналогичны.
Однако, если стены лаборатории «раздвинуть», скажем, на 100 километров, то они уже не будут параллельны, а её пол станет частью сферы, все точки которой одинаково удалены от центра Земли. Теперь, чтобы сохранить движение тела прямолинейным, придется оторвать его от сферической поверхности, значит – применить силу. Поэтому прямолинейное движение по инерции невозможно. Именно об этом и упоминалось в беседе о выборе системы отсчёта.
При этом следует помнить, что горизонтальной можно считать только ту поверхность, в любой точке которой радиус силового поля всегда перпендикулярен к ее элементарному участку. Именно поэтому в силовом (потенциальном) поле горизонтальная поверхность является сферой (или ее частью) с одинаковым потенциалом (гравитационным или электрическим). Такую сферу мы называем эквипотенциальной.
С учетом этих определений Закон инерции следует читать в более общей редакции:
«Всякое тело сохраняет инерционное движение по эквипотенциальной поверхности, если только оно не вынуждено изменять его под влиянием действующих сил».
Однако, это всего лишь более общая формулировка, а мы с Вами, коллега, знаем, что в практике неплохо действует и формулировка Ньютона.
Я уже говорил, что в рамках лаборатории (силовое поле практически однородно) условия для движения по Галилею и Ньютону почти аналогичны.
Однако, для явно выраженных неоднородных полей формулировка Ньютона неприемлема. И наоборот, использование более общей формулировки в этом случае позволяет нам, к примеру, обойтись без постулатов Бора, которые он вынужденно положил в основу теории атома водорода. Раз электрон в потенциальном поле атома движется по поверхности одинакового потенциала (по инерции), то его энергия (потенциальная и кинетическая) не изменяется и он не должен её излучать. Несколько позже мы поговорим об этом подробнее.
Примеры инерции
Определение и общие принципы инерции
Основная задача механики – это исследование движения тел относительно избранной системы отсчета и установка причин, которые определяют характер движения. Следует установить, в каких условиях тело перемещается по прямой линии, а в каких его траекторией является кривая, когда тело движется с постоянной скоростью, когда имеет ускорение.
Эксперимент устанавливает, что если тела взаимодействуют, то характер движения тел изменяется. Например, тело падает, при соприкосновении с Землей оно остановится или изменит направление своего движения на противоположное (подпрыгнет). Находящееся в покое, по отношению к Земле, тело самостоятельно никогда не станет перемещаться само, оно начнет движение только под действием другого тела.
Следует заметить, что вывод о том, что взаимодействие тел ведет к изменению их скорости перемещения. Так, Аристотель считал, что само движение возможно только во взаимодействии с другими телами. Причиной ошибки служило то, что Земля в то время считалась неподвижным центром Вселенной. Состояние покоя относительно Земли считалось естественным, а движение вынужденным состоянием, для которого необходимо воздействие внешних сил.
К концу XIV века проблема движения была актуализирована, так как развивалась артиллерия, и следовало объяснить законы движения снарядов. Кроме этого появилась гелиоцентрическая система Коперника, в которой центром Вселенной стало Солнце, а Земля – это рядовая планета, вращающаяся вокруг него. Возник вопрос: что толкает Землю и другие планеты, заставляя двигаться миллиарды лет? Требовало объяснения тот факт, что люди не чувствуют вращения Земли и оторвавшись от Земли человек опустится в ту же точку, откуда, например, подпрыгнул.
Первое верное, но неполное решение проблемы представил Галилей. Идея мысленного эксперимента с телом, на которое не воздействуют никакие тела, дала возможность ученому выдвинуть гипотезу инерциального движения тела. Галилей был прав, когда предположил, что по инерции тело может двигаться равномерно и прямолинейно, но ошибся, когда решил, что тело может двигаться равномерно по окружности.
Закон инерции
Закон инерции окончательно сформулировал Ньютон (первый закон Ньютона): Если на тело не действуют другие тела, то скорость его перемещения не изменяется по модулю и направлению (тело движется равномерно и прямолинейно или покоится).
Движение по инерции – это перемещение по кратчайшему пути, в свободном пространстве кратчайшим расстоянием между двумя точками является прямая. Если мы утверждаем, что тело находится в покое, то покой считать абсолютным нельзя. Это состояние тела только относительно отдельной системы отсчета, которая сама движется относительно других тел.
В результате существования инерции, подпрыгнув вверх в вагоне мы опустимся на тоже место. Стоя на полу вагона, перемещающегося с постоянной скоростью, мы обладаем такой же скоростью. Подпрыгнув вверх, мы сохраним горизонтальную скорость без изменения, так как в направлении горизонта на нас не действуют другие тела. Следовательно, за момент прыжка мы проходим по горизонтали такой же путь, как и вагон, и возвращаемся в туже точку, с которой мы совершили прыжок. Аналогично можно рассмотреть наше движение вместе с Землей.
По инерции перемещаются тела, которые бросили. Бросая камень, мы сообщаем ему некоторую скорость в момент броска. В том случае, если бы сопротивления воздуха и силы притяжения к Земле не было бы, то камень мог бы двигаться по инерции без изменения скорости по модулю и направлению бесконечно долго.
Если заставить тело скользить по поверхности, то чем более гладкая поверхность, тем медленнее уменьшает скорость тело. На гладком льду тело скользит долго, не изменяя скорость. Трение можно уменьшить до минимума (почти до нуля) если использовать воздушную подушку (струю воздуха, которая будет поддерживать тело над поверхностью, вдоль которой идет движение).
Подведем итоги. Инерцией называют явление, при котором скорость тела остается неизменной, если на него не действуют другие тела или их действие взаимно компенсируются. Inertia — от латинского бездеятельность, косность.
Явление инерции становится очевидным тогда, когда изменяется величина или направление скорости движения. Так, при уменьшении скорости движения автомобиля, особенно, если это происходит резко, водитель и пассажиры отклоняются вперед, продолжая движение. Если резко затормозить при езде на велосипеде, то можно перелететь через его руль вперед. Инерция – это свойство материи, все тела обладают свойством инерции.
Если любое тело вывести из состояния покоя, то после прекращения воздействия на него, оно будет двигаться по инерции. Явление инерции проявляется повсюду.
Примеры решения задач на инерцию
| Задание | Приведите примеры инерциальных систем отсчета. Является ли система отсчета, связанная с Землей инерциальной? |
| Решение | Для начала дадим определение инерциальной системы отсчета. Инерциальной системой отсчета называют такую систему отсчета, относительно которой свободное тело (тело на которое не оказывают воздействие другие тела) покоится или движется равномерно и прямолинейно называется инерциальной. Любая другая система отсчета, которая перемещается относительно инерциальной с постоянной по модулю и направлению скоростью, тоже является инерциальной. |
Инерциальной системой отсчета можно считать систему, в которой начало координат совмещают с центром Солнца, оси координат направлены к неподвижным звездам (рис.1). Такую систему называют гелиоцентрической.
Систему отсчета, связанную с поверхностью Земли можно считать инерциальной только условно, так как Земля вращается вокруг собственной оси, значит, имеет ускорение. Система отсчета, которую жестко связывают с центром Земли, более близка к инерциальной, так как ее ускорение при движении вокруг Солнца существенно меньше, чем центростремительное ускорение при вращении Земли вокруг оси.
| Задание | Существует ряд забавных экспериментов, в которых демонстрируется явление инерции. Например, такой. На край стола укладывают лист бумаги. Сверху на бумагу ставим столбик из нескольких монеток. Тянем за листок медленно, монеты перемещаются вместе с листком. Дергаем резко бумагу. Листок можно выдернуть из под монет. При этом монеты останутся стоять на столе столбиком. Начинать этот опыт следует с небольшого количества монет. |
Поставим на стол тележку на колесиках. Толкнем ее, тележка станет перемещаться в горизонтальной плоскости. Поставим на тележку деревянный брусок (материал бруска значения не имеет). Резко толкнем тележку, при этом брусок упадет назад из-за существования явления инерции.