Что такое дуга в информатике
Дуга (теория графов)
Здесь собраны определения терминов из теории графов. Курсивом выделены ссылки на термины в этом словаре (на этой странице).
Ссылки
Литература
Полезное
Смотреть что такое «Дуга (теория графов)» в других словарях:
Граф (теория графов) — Неориентированный граф с шестью вершинами и семью рёбрами В математической теории графов и информатике граф это совокупность объектов со связями между ними. Объекты представляются как вершины, или узлы графа, а связи как дуги, или рёбра. Для… … Википедия
Дерево (теория графов) — У этого термина существуют и другие значения, см. Дерево (значения). Дерево это связный ациклический граф.[1] Связность означает наличие путей между любой парой вершин, ацикличность отсутствие циклов и то, что между парами вершин… … Википедия
Цикл (теория графов) — Здесь собраны определения терминов из теории графов. Курсивом выделены ссылки на термины в этом словаре (на этой странице). # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф … Википедия
Дуга — Дуга: В математике Дуга (геометрия) участок кривой между двумя её точками. Дуга окружности кривая линия, лежащая на окружности и ограниченная двумя точками. Дуга (теория графов) Другое Дуга (география) Дуга (анатомия) Дуга (физика) Дуга… … Википедия
ГРАФОВ ТЕОРИЯ — в химии, область конечной математики, изучающая дискретные структуры, наз. графами; применяется для решения различных теоретич. и прикладных задач. Некоторые основные понятия. Граф совокупность точек (вершин) и совокупность пар этих точек (не… … Химическая энциклопедия
Глоссарий теории графов — Эта страница глоссарий. См. также основную статью: Теория графов Здесь собраны определения терминов из теории графов. Курсивом выделены ссылки на термины в этом словаре (на этой странице) … Википедия
Словарь терминов теории графов — Здесь собраны определения терминов из теории графов. Курсивом выделены ссылки на термины в этом словаре (на этой странице). # А Б В Г Д Е Ё Ж З И К Л М Н О П Р С … Википедия
Граф (математика) — У этого термина существуют и другие значения, см. Граф (значения). Неориентированный граф с шестью вершинами и семью рёбрами В математической теории графов и информатике граф это совокупность непустого множества вершин и множества пар… … Википедия
Теория Графов. Часть 1 Введение и классификация графов
«Графы являются одним из объединяющих понятий информатики – абстрактное представление, которое описывает организацию транспортных систем, взаимодействие между людьми и телекоммуникационные сети. То, что с помощью одного формального представления можно смоделировать так много различных структур, является источником огромной силы для образованного программиста». Стивен С. Скиена
Введение
Сначала под землей города Москвы ничего не было. Потом была построена первая станция метро, а затем и вторая и третья. Образовалось множество станций метро. На карту было занесено множество точек. Позже между станциями стали прокладывать пути линии. И соединилась станция метро А со станцией метро Б. Все остальные станции также стали соединятся друг с другом и на карте появилось множество линий. В итоге мы имеем Московский метрополитен очень красивый, я там был проверял.

Посмотрите какая красота. У нас имеется множество точек (которые называются вершинами или узлами), а также множество линий (называемые рёбрами или дугами). Обозначим множество вершин буквой V от английского vertex−вершина и множество рёбер обозначим E от английского edge−ребро. Граф в формулах именуют буквой G. Все вершины обязательно должны быть идентифицированы.
Отмечу, что число вершин обозначается буквой n:
Число рёбер обозначается буквой m:
Таким образом граф задается и обозначается парой V,E:
Также определение графа рассказывается в этой статье на Хабре (https://habr.com/ru/post/65367/)
Неформально граф является совокупностью точек и линий. Линии в котором задаются парой вершин, расположенных не важно в каком порядке.
Разберем определение графа подробней. Может ли в G быть пустым множество E? Да без проблем! Такой граф будет называться нулевым, а вершины в нем будут называться изолированными.

Только вот множество V вершины пустым быть не может. Ведь множество E рёбра задается парой неупорядоченных вершин множества V. Две вершины образующие ребро, называются концами этого ребра.
Множество E задается парой неупорядоченных вершин множества V.
Пример: Пусть множество V = <1,2,3,4,5>. Тогда множество E =
Граф будет выглядеть следующим образом:
Висячей вершиной называется вершина которая соединена только с одной соседней вершиной. В нашем случаи висячей вершиной будет вершина 5, так как она соединена только с вершиной 1.
Степень записывают, как:
Максимальная степень, то есть какое количество степеней вообще присутствуют в графе обозначаются, как:
Формула суммы степеней для G = V,E выглядит так:
То есть сумма степеней всех вершин v графа равна удвоенному количеству его рёбер E. Считаем количество степеней в нашем примере. От этого никуда не денешься. Я насчитал 12. А теперь считаем, сколько у нас рёбер. Их 6! Умножаем на 2 и получаем 12. Совпадение? Не думаю!
А давайте представим наш граф в другом виде, но с сохранением данных пар. G теперь имеет следующий вид:
Заметьте я не изменил пары между собой. Вершина 4 также соединяется с вершиной 3, а у вершины 1 степень также осталась 4. Так почему граф имеет совершенно другой вид и законно ли это?
Классификации графов
Первым признаком классификации является отсутствие или наличие ориентации у ребер.
Ребро является неориентированным если у него нет понятия начала или конца. То есть оба его конца равноправны. Такой граф называется неориентированным, обыкновенным или неографом.

Ориентированное ребро обозначается стрелкой. И указывает ориентацию от вершины к вершине. То есть данный граф имеет начало и конец. И называется он ориентированным или орграфом.

Также существует граф со смешанными ребрами. Это когда в графе присутствуют, как ориентированные рёбра, так и неориентированные.

Вторым признаком является отсутствие или наличие кратных ребер.

Граф в котором кратных ребер нет, является простым графом. В простом графе мы просто называем пару вершин для идентификации ребра, но в мультиграфе такое уже не сработает, так как одна и та же пара вершин будет указывать на два ребра и не понятно что к чему будет относится. Поэтому если вы повстречаете мультиграф, то вы должны обозначить каждое ребро отдельно.
Заключение
В данной стать я не рассмотрел, понятия смежности и инцидентности, однако я решил их рассмотреть в следующий раз. Также хочу отметить, что более подробно виды графов, я буду рассматривать в следующих статьях. Если у вас есть вопросы, предложения или я где-то допустил ошибки, то прошу написать их в комментариях.
Что такое дуга в информатике
Вид оборудования для транспортировки энергоносителей выбирается из набора стандартных сооружений. Пронумеруем их и обозначим через а т стоимость использования дуги графа П, [c.332]
Множество дуг графа (i, j) e С/ определим по рис. 3. Для наглядности изображения положим п = 2, Г=6. Интенсивности вершин обведены кружками. Нейтральные вершины изображены точками. [c.55]
Приведем краткое описание модели, основанной на стохастическом графе с возвратом. Стохастический ориентированный граф с возвратом будем обозначать через G (I, U), где /— множество вершин, U — множество дуг графа G. Граф G (I, U) имеет следующие свойства [c.195]
Множество дуг [/графа G (I, U) неоднородно и состоит из дуг типа [c.195]
Положим длины дуг графа РВЗ равными затратам на оплату [c.32]
ДУГА ГРАФА [ar ] — см. Граф. [c.97]
Вычислительные алгоритмы представляются взвешенными ориентированными ациклическими графами [72] (рис. 1.39). Вершины таких графов соответствуют некоторым частям алгоритма, в дальнейшем называемыми операциями. Дуги графа, соединяющие вершины, означают наличие информационной зависимости между соответствующими операциями алгоритма — результат выполнения одной операции является аргументом для другой. Веса вершин пропорциональны времени выполнения соответствующих операций — будем измерять их числом некоторым элементарных операций, содержащихся в соответствующей данной вершине операции. Под элементарной операцией можно понимать, например, арифметическую операцию (сложения/умножения) или один такт процессора. Дуги графа алгоритма также являются взвешенными, и их вес равен объему (например, в байтах) передаваемой по этой дуге информации. [c.137]
Каждую дугу графа будем представлять в виде упорядоченной пары номеров вершин (i,j), которые эта дуга соединяет. [c.137]
Каждая из дуг графа обозначает пересылку одного трехмерного массива, поэтому вес всех дуг равен N слов, и если положить, что 1 слово = 4 байтам, то вес дуг равен 64N Бт. [c.164]
Проведен численный анализ зависимости ускорения, достигаемого при распараллеливании явного метода решения системы нелинейных динамических систем от параметров ВС — числа процессоров и скорости работы каналов обмена данными. Так как веса всех вершин и дуг графа этого алгоритма суть величины одного порядка по N (где N есть размерность задачи), то увеличение N, в отличие от рассмотренных выше алгоритмов линейной алгебры, на ускорение никак не влияет. По причине больших объемов передаваемых данных при выполнении алгоритма ускорение больше 1 достигается только на очень высоких (относительно производительности процессоров) скоростях каналов, что делает рассмотренный метод мало пригодным к выполнению на большинстве реальных [c.166]
Однако наибольший интерес представляет второй способ его задания — графический. Зададим на плоскости множество Nn виде кружков и множество А в виде линий, соединяющих эти кружки. Тогда тот же граф будет иметь вид, представленный на рис. 4.8. Ребро считается ориентированным, если порядок следования вершин в соответствующей паре (ij) A строго задан. Такие пары называются дугами графа и изображаются на рисунках стрелками. Граф G (N, А) называется ориентированным, если все элементы его множества А — дуги. [c.121]
При параллельном соединении блоков в подсистему цель ее формируется одновременным достижением целей входящих в нее блоков, которые состоят с целью подсистемы в определенных отношениях. Связями между целями элементарных блоков и целью подсистемы при этом служат дуги графа целей R. Цель Ц»Г1 достигается, если достигнуты » 1Пз (рис.15). [c.59]
Какая бы процедура не использовалась, в результате должен быть получен список концептов (вершин знакового графа), список отношений причинности (дуг графа) и список значений отношений [c.182]
Задача генерации всех возможных сценариев может быть решена различными методами. Все они, так или иначе, сводятся к перебору дуг графа, описывающего создавшуюся проблему. Поэтому решение задачи могло бы быть дано и в терминах теории графов. Однако с точки зрения перспектив решения подобных задач для графов со значительно более сложной структурой (например, когда на элементы графа накладываются различные условия) более перспективным может оказаться использование аппарата формальных грамматик. [c.186]
Элементы и множество связей между ними и их признаками могут быть представлены в форме графа, носящего название И—ИЛИ дерева [1]. На нем в виде вершин изображаются структурные элементы, в качестве которых могут быть узлы, детали, части деталей. На этом же графе рядом со структурной вершиной изображаются вершины признаков. Вершины могут быть двух видов И или ИЛИ. На графе они имеют разное обозначение. Дуги графа означают связи между структурными элементами. И—ИЛИ дерево может относиться как к одной конкретной технической системе, так и к целой их совокупности. В последнем случае каждой технической системе соответствует конкретный путь от основания дерева к его вершине. [c.128]
Поскольку подсистема бухгалтерского учета представляет собой взаимосвязанный набор комплексов учетных задач, сгруппированных по признаку однородности массивов информации в отдельные блоки, все задачи могут быть представлены в виде связного графа, в котором каждая задача является вершиной графа, а дуги графа указывают взаимосвязи задачи, т. е. возможное использование информации одной задачи для решения другой. [c.35]
Как уже отмечалось, классификация адаптивных свойств в целом представляет собой древовидный ориентированный граф. Каждая из вершин этого графа представляет адаптивное свойство того или иного уровня в классификационной иерархии, корень графа — полное множество адаптивных свойств АСУ. Множество дуг графа является отображением разбиения отдельных подмножеств адаптивных свойств на подмножества адаптивных свойств иерархически более низкого уровня (ранга) или элементарные адаптивные свойства, т. е. такие, которые не являются совокупностью двух или более других адаптивных свойств. Отметим, что ранг элементарных адаптивных свойств равен 1. [c.33]
Vi=0,5 V2=0,3 V3=0,2. В результате определены веса всех дуг графа, изображенного на рис. 26. [c.37]
Примерами графа являются 1) сети железных дорог (вершины — ж.-д. узлы, а рёбра — рельсовые пути) 2) схемы шоссейных дорог. Часто рёбрам графа приписывается ориентация (направление), т. е. указывается начальная п конечная вершины рёбер, тогда элементы из U наз. дугами графа, а сам граф [c.111]
На рис. 4.4. точки принятия решения о выборе стратегии или наборе базовых стратегий соответствуют вершинам графа, а условия работы предприятия соответствуют движению вдоль дуг графа. Каждой точке принятия решения поставлен в соответствие некоторый набор стратегий, рекомендуемых предприятию. Если это не так, то для принятия решения требуется дополнительная информация об условиях работы предприятия, что соответствует обязательному переходу к следующей вершине графа. [c.110]
Определим веса дуг графа как алгебраическую сумму относительных приростов (потерь) критериев системы при переходе от управления ип к [c.129]
Дуги графа помечены степенями принадлежности ц. которые ассоциируются с возможностью переходов из одного состояния в другое. Граф строится на основании экспертных данных и отображает реальные представления о смене графических изображений. Функцию принадлежности любому из состояний будем [c.182]
Функция создания и корректировки когнитивной карты (в). Для реализации необходимо 1) задать вершины графа, представляющие собой элементы когнитивной карты 2) задать дуги графа, представляющие собой отношения между элементами когнитивной карты 3) задать текущие значения параметров вершин графа 4) представить и отобразить на экране дисплея созданный ориентированный граф 5) сохранить данные построенного графа в файле на жестком диске для последующего использования построенной когнитивной карты. [c.221]
Чтобы произвести оценку риска банкротства количественно и качественно, необходимо произвести агрегирование данных, собранных в рамках древовидной иерархии при этом агрегирование совершается по направлению дуг графа иерархии. [c.35]
Легко представить эту задачу с помощью графа. Населенные пункты представляются вершинами графа, а шоссейные дороги—дугами, которые их соединяют. Станция технического обслуживания должна быть расположена на одной из дуг графа. [c.265]
Улицы представляются дугами некоторого графа. Задача почтальона заключается в том, чтобы найти маршрут обхода всех дуг графа минимальной длины. [c.265]
Поток на графе — это совокупность однородных объектов, пересылаемых из одной вершины в. другую по его дугам. Если вершины р и q соединены дугой а — (р, q), то поток из р в щ обозначается f(p, q). Таким образом, поток — это некоторая функция, заданная на дугах графа. [c.266]
Алгоритм поиска Кратчайшего пути В ходе выполнения алгоритма окрашивают вершины и дуги графа и вычисляют величины d(x), равные кратчайшему пути из вершины s в вершину х, включающему только окрашенные вершины. [c.270]
Функциональная модель подсистемы, цель которой формируется объединением нескольких целей нижележащего уровня (параллельное соединение блоков), может быть образована установлением функциональных связей между векторами, характеризующими каждую из исходных целей, с векторами, отражающими цель подсистемы, (см. рис. 13). В качестве таких связей используют отношения между указанными целями, т. е. дуги (г) графа целей, так как множества этих дуг являются отношениями условий достижения целей верхнего уровня и условием Я. Например, цель Z(«j достигается, [c.35]
Наиболее рациональным приемом анализа и расчета параметров корреляционной связи с помощью группировки является построение так называемой корреляционной решетки (табл. 8.3). Это таблица, в которой изучаемая совокупность сгруппирована одновременно по обоим признакам, связь между которыми изучается (двумерное распределение). Число групп по признакам может быть как равным, так и неравным. Если наибольшие числа частот каждой строки и каждого столбца располагаются на первой диагонали (в табл. 8.3 эти цифры подчеркнуты), связь является прямой и близкой к линейной если наибольшие числа частот располагаются вдоль второй диагонали (в табл. 8.3 эти цифры также подчеркнуты), связь обратная, линейная. Если частоты во всех клетках таблицы примерно равны, связи нет если наибольшие числа расположены по дуге, связь криволинейная. В табл. 8.3 кроме частот приведены строки и графы [c.255]
В простейшем случае рассмотрение может быть сведено к системе из двух элементов проект и организатор. Подобная схема приведена на рис. 2.1, вершины графа изображены прямоугольниками, а дуги помечены названиями денежных потоков. Под «проектом» в данной схеме понимается достаточно сложная система, которая включает в себя производственные мощности проекта, трудовые ресурсы, поставщиков, подрядные организации, покупателей продукции проекта и другие элементы, которые необходимы для организации производства и сбыта продукции проекта. Все эти элементы удобно объединить в одну систему, называемую «проект», и уже для нее производить оценку денежных потоков. [c.41]
Внутри любого узла (кроме виртуального узла parent) происходит обработка транзакта, определяемая спецификой его типа. Дуги графа представляют собой пути миграции транзактов по графу модели и имеют направленность. Возможны ситуации, когда один узел имеет несколько выходов, тогда путь транзакта определяется условиями, заданными в узле-источнике. [c.165]
Для определения понятия ациклической схемы БД введем граф соединений на множестве отношений (SI, S2. Sk). Вершинами графа соединений являются имена существующих отношений SI, S2. Sk. Дуга графа существует, если в структуре отношений Si и Sj имеются общие атрибуты. Обозначим их для определенности через A(i j) и назовем весом дуги. Путь на графе соединений называется А-путем, если атрибут А содержится в структуре каждого отношения, лежащего на пути. В графе соединений требуется, чтобы для каждой пары отношений Si, Sj с общим атрибутом A(i,j) существовал A(i j)-nyrb между Si и Sj. [c.93]
Что такое дуга в информатике?
Что такое графа в информатике?
Графом называется конечное множество вершин и множество ребер. Каждому ребру сопоставлены две вершины – концы ребра. Бывают различные варианты определения графа.
Для чего нужны графы в информатике?
Графы используют в связи с развитием теории вероятности, математической логики и информационных технологий. Граф — это конечная совокупность вершин, некоторые из которых соединены ребрами, т. е.
Что такое вершина в информатике?
В теории графов вершиной называется фундаментальная единица, образующая графы — неориентированный граф состоит из множества вершин и множества рёбер (неупорядоченных пар вершин), в то время как ориентированный граф состоит из множества вершин и множества дуг (упорядоченных пар вершин).
Что такое взвешенный граф в информатике?
Взвешенный граф — граф, каждому ребру которого поставлено в соответствие некое значение (вес ребра). Граф называется неориентированным, если его вершины соединены рёбрами. Цепь — путь по вершинам и рёбрам, включающий любое ребро графа не более одного раза. Цикл — цепь, начальная и конечная вершины которой совпадают.
Какие бывают графы в информатике?
Какие виды графов бывают информатика?
Что такое графы и для чего они нужны?
Граф — математическая абстракция реальной системы любой природы, объекты которой обладают парными связями. Граф как математический объект есть совокупность двух множеств — множества самих объектов, называемого множеством вершин и множеством их парных связей, называемой множеством рёбер.
Для чего нужны графы в математике?
Термин «граф» в математике определяется следующим образом: Граф– это конечное множество точек – вершин, которые могут быть соединены линиями – ребрами. В качестве примеров графов могут выступать чертежи многоугольников, электросхемы, схематичное изображение авиалиний, метро, дорог и т.
Какие графы бывают?
Что такое иерархия в информатике?
Что такое граф из чего он состоит?
Что такое висячие вершины?
Вершина называется изолированной, если её степень равна нулю. То есть это вершина, не являющаяся конечной ни для какого ребра. Вершина называется листом (или висячей), если имеет степень единица.
Как определить является ли граф взвешенным?
Под взвешенным графом понимается граф, у которого рёбрам соответствуют некоторые весовые параметры. То есть каждому ребру (дуге) поставлено в соответствие некое числовое значение, которое называется длина дуги (или вес, стоимость).
Какой граф является взвешенным?
Взвешенный граф — граф, каждому ребру которого поставлено в соответствие некое значение (вес ребра). См. Размеченный граф. Вполне несвязный граф (пустой граф, нуль-граф) — регулярный граф степени 0, то есть граф без рёбер.
Что такое взвешенный график?
Взвешенный граф — это граф, дугам которого поставлены в соответствие веса, так что дуге (xif xj) сопоставлено некоторое число с (xjy Xj) = называемое длиной (или весом, или стоимостью) дуги (табл. 3.9). Обычный (не взвешенный) граф можно интерпретировать как взвешенный, все ребра которого имеют одинаковый вес 1.
Теория графов. Основные понятия и виды графов.
Перед тем как начать изучение непосредственно алгоритмов, необходимо обладать базовыми знаниями касательно самих графов, понимать, как они представляются в компьютере. Здесь не будут подробно описаны все аспекты теории графов (этого и не требуется), но только те, незнание которых заметно усложнит усвоение данной области программирования.
Несколько примеров дадут немного поверхностного представления о графе. Так типичным графом является схема метро или какой-либо другой маршрут. В частности программисту знакома компьютерная сеть, также являющаяся графом. Общее здесь это наличие точек, соединенных линиями. Так в компьютерной сети точки – это отдельные серверы, а линии – различные виды электрических сигналов. В метрополитене первое – станции, второе – туннели, проложенные между ними. В теории графов точки именуется вершинами (узлами), а линии – ребрами (дугами). Таким образом, граф – это совокупность вершин, соединённых ребрами.
Математика оперирует не содержанием вещей, а их структурой, абстрагируя ее из всего того, что дано как целое. Пользуясь именно этим приемом, мы можем заключать о каких-либо объектах как о графах. А поскольку теория графов это часть математики, то для нее нет абсолютно никакого значения, что в принципе представляет собой объект; важно лишь то, является ли он графом, т. е. обладает ли обязательными для графов свойствами. Поэтому, прежде чем привести примеры, мы выделяем в рассматриваемом объекте лишь то, что как нам кажется, позволит показать аналогию, отыскиваем общее.
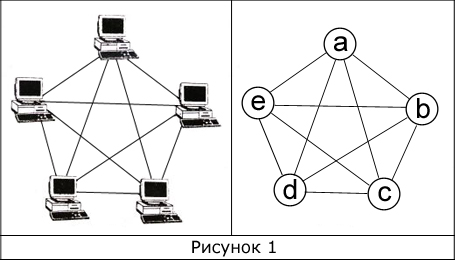
Вернемся к компьютерной сети. Она обладает определенной топологией, и может быть условно изображена в виде некоторого числа компьютеров и путей их соединяющих. На рисунке ниже в качестве примера показана полносвязная топология.
Это по сути граф. Пять компьютеров являются вершинами, а соединения (пути передачи сигналов) между ними – ребрами. Заменив компьютеры вершинами, мы получим математический объект – граф, который имеет 10 ребер и 5 вершин. Пронумеровать вершины можно произвольным образом, а не обязательно так, как это сделано на рисунке. Стоит отметить, что в данном примере не используется ни одной петли, то есть такого ребра, которое выходит из вершины и сразу же входит в нее, но петли могут встречаться в задачах.
Вот некоторые важные обозначения, используемые в теории графов:
В нашем случае (рис. 1) |V|=5, |E|=10;
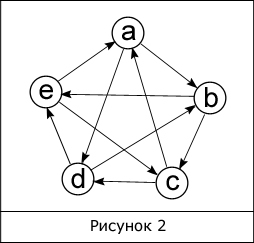
Когда из любой вершины доступна любая другая вершина, то такой граф называется неориентированным связным графом (рис. 1). Если же граф связный, но это условие не выполняется, тогда такой граф называется ориентированным или орграфом (рис. 2).
В ориентированных и неориентированных графах имеется понятие степени вершины. Степень вершины – это количество ребер, соединяющих ее с другими вершинами. Сумма всех степеней графа равна удвоенному количеству всех его ребер. Для рисунка 2 сумма всех степеней равна 20.
В орграфе, в отличие от неориентированного графа, имеется возможность двигаться из вершины h в вершину s без промежуточных вершин, лишь тогда когда ребро выходит из h и входит в s, но не наоборот.
Ориентированные графы имеют следующую форму записи:
G=(V, A), где V – вершины, A – направленные ребра.
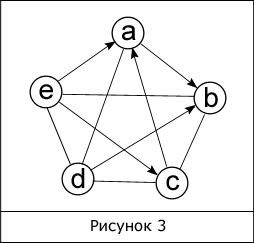
Третий тип графов – смешанные графы (рис. 3). Они имеют как направленные ребра, так и ненаправленные. Формально смешанный граф записывается так: G=(V, E, A), где каждая из букв в скобках обозначает тоже, что ей приписывалось ранее.
В графе на рисунке 3 одни дуги направленные [(e, a), (e, c), (a, b), (c, a), (d, b)], другие – ненаправленные [(e, d), (e, b), (d, c)…].
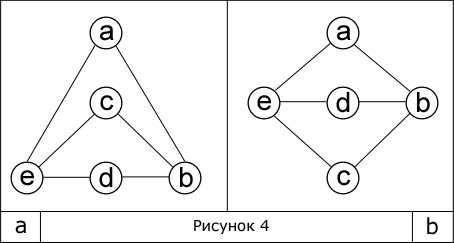
Два или более графов на первый взгляд могут показаться разными по своей структуре, что возникает вследствие различного их изображения. Но это не всегда так. Возьмем два графа (рис. 4).
Они эквивалентны друг другу, ведь не изменяя структуру одного графа можно построить другой. Такие графы называются изоморфными, т. е. обладающими тем свойством, что какая-либо вершина с определенным числом ребер в одном графе имеет тождественную вершину в другом. На рисунке 4 изображены два изоморфных графа.
Когда каждому ребру графа поставлено в соответствие некоторое значение, называемое весом ребра, тогда такой граф взвешенный. В разных задачах в качестве веса могут выступать различные виды измерений, например длины, цены маршруты и т. п. В графическом представлении графа весовые значения указываются, как правило, рядом с ребрами.
В любом из рассмотренных нами графов имеется возможность выделить путь и, причем не один. Путь – это последовательность вершин, каждая из которых соединена с последующей посредством ребра. Если первая и последняя вершины совпадают, то такой путь называется циклом. Длина пути определяется количеством составляющих его ребер. Например, на рисунке 4.а путем служит последовательность [(e), (a), (b), (c)]. Этот путь является подграфом, так как к нему применимо определение последнего, а именно: граф G’=(V’, E’) является подграфом графа G=(V, E), только тогда когда V’ и E’ принадлежат V, E.
Способы представления графов.
Граф, как и большинство других математических объектов, может быть представлен на компьютере (сохранен в его памяти). Существуют несколько способов его интерпретации, вот наиболее известные из них:
Использование двух первых методов предполагает хранение графа в виде двумерного массива (матрицы). Причем размеры этих массивов, зависят от количества вершин и/или ребер в конкретном графе. Так размер матрицы смежности n×n, где n – число вершин, а матрицы инцидентности n×m, n – число вершин, m – число ребер в графе.