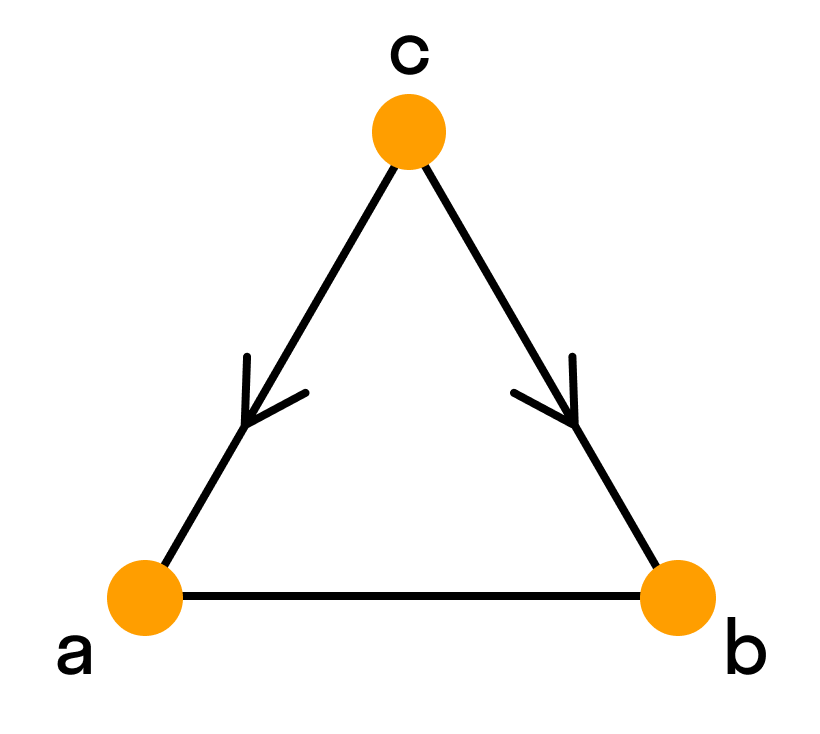
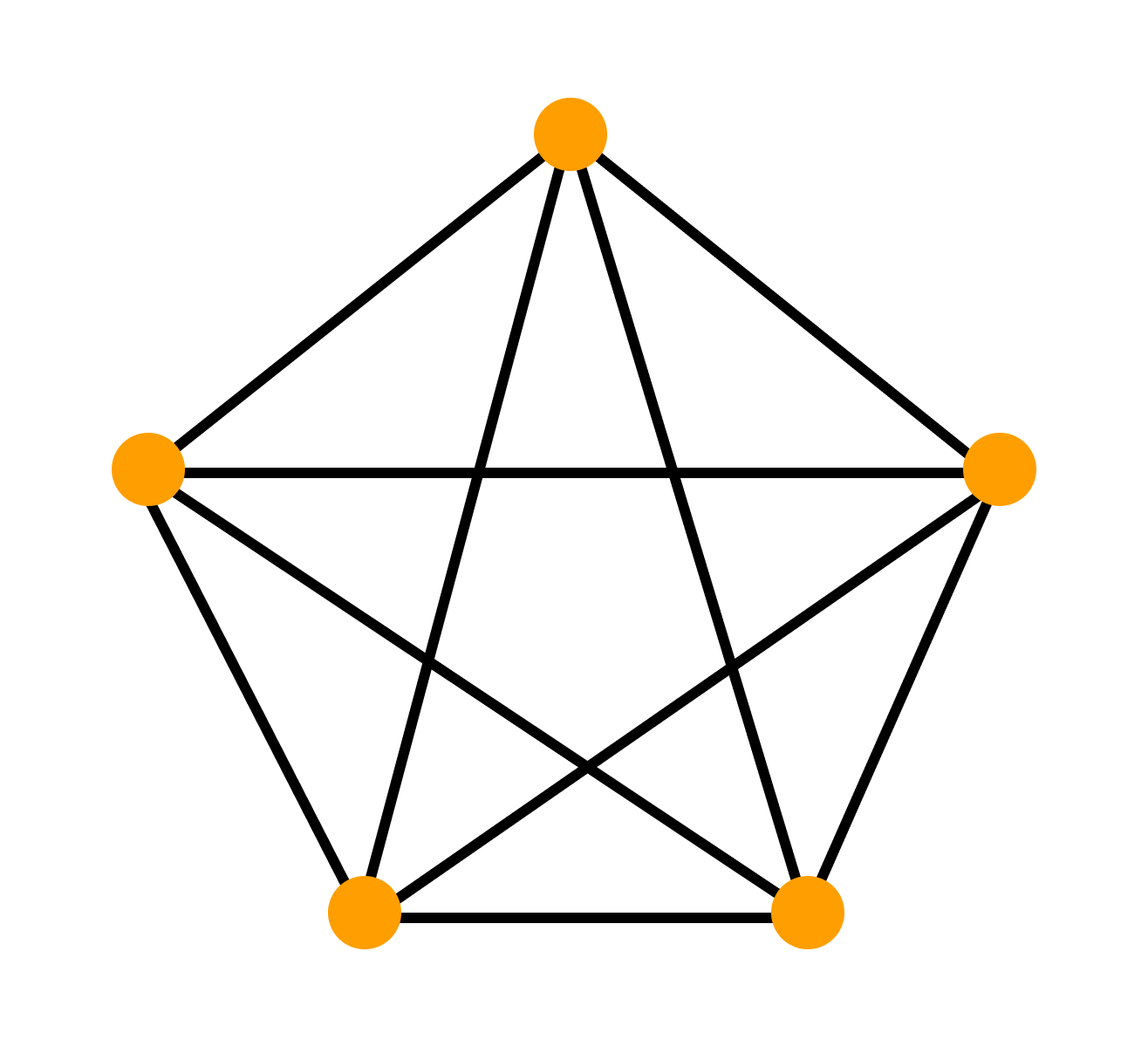
Что такое дуга графа
Дуга (теория графов)
Здесь собраны определения терминов из теории графов. Курсивом выделены ссылки на термины в этом словаре (на этой странице).
Ссылки
Литература
Полезное
Смотреть что такое «Дуга (теория графов)» в других словарях:
Граф (теория графов) — Неориентированный граф с шестью вершинами и семью рёбрами В математической теории графов и информатике граф это совокупность объектов со связями между ними. Объекты представляются как вершины, или узлы графа, а связи как дуги, или рёбра. Для… … Википедия
Дерево (теория графов) — У этого термина существуют и другие значения, см. Дерево (значения). Дерево это связный ациклический граф.[1] Связность означает наличие путей между любой парой вершин, ацикличность отсутствие циклов и то, что между парами вершин… … Википедия
Цикл (теория графов) — Здесь собраны определения терминов из теории графов. Курсивом выделены ссылки на термины в этом словаре (на этой странице). # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф … Википедия
Дуга — Дуга: В математике Дуга (геометрия) участок кривой между двумя её точками. Дуга окружности кривая линия, лежащая на окружности и ограниченная двумя точками. Дуга (теория графов) Другое Дуга (география) Дуга (анатомия) Дуга (физика) Дуга… … Википедия
ГРАФОВ ТЕОРИЯ — в химии, область конечной математики, изучающая дискретные структуры, наз. графами; применяется для решения различных теоретич. и прикладных задач. Некоторые основные понятия. Граф совокупность точек (вершин) и совокупность пар этих точек (не… … Химическая энциклопедия
Глоссарий теории графов — Эта страница глоссарий. См. также основную статью: Теория графов Здесь собраны определения терминов из теории графов. Курсивом выделены ссылки на термины в этом словаре (на этой странице) … Википедия
Словарь терминов теории графов — Здесь собраны определения терминов из теории графов. Курсивом выделены ссылки на термины в этом словаре (на этой странице). # А Б В Г Д Е Ё Ж З И К Л М Н О П Р С … Википедия
Граф (математика) — У этого термина существуют и другие значения, см. Граф (значения). Неориентированный граф с шестью вершинами и семью рёбрами В математической теории графов и информатике граф это совокупность непустого множества вершин и множества пар… … Википедия
Что такое дуга графа
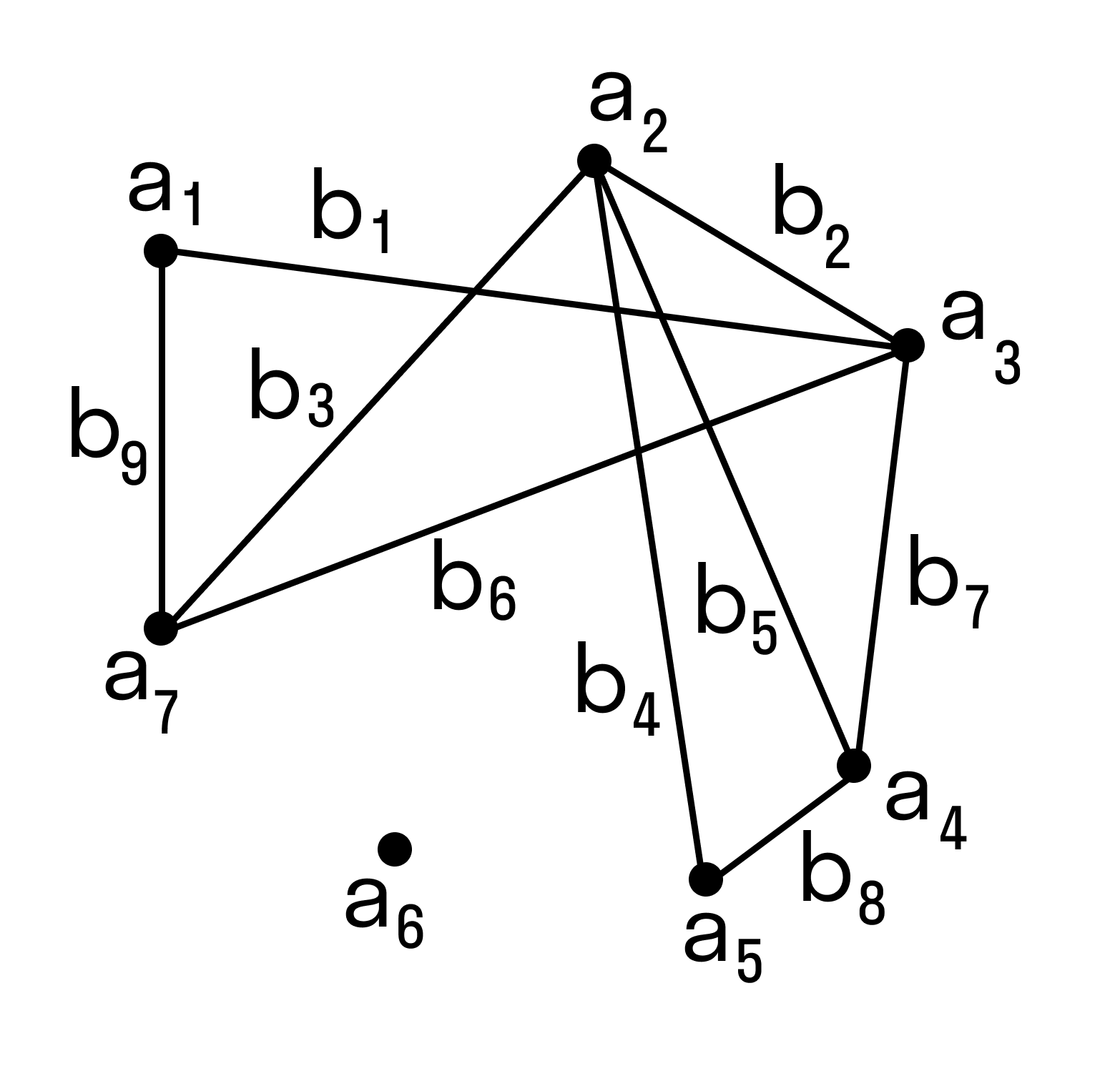
Вид оборудования для транспортировки энергоносителей выбирается из набора стандартных сооружений. Пронумеруем их и обозначим через а т стоимость использования дуги графа П, [c.332]
Множество дуг графа (i, j) e С/ определим по рис. 3. Для наглядности изображения положим п = 2, Г=6. Интенсивности вершин обведены кружками. Нейтральные вершины изображены точками. [c.55]
Приведем краткое описание модели, основанной на стохастическом графе с возвратом. Стохастический ориентированный граф с возвратом будем обозначать через G (I, U), где /— множество вершин, U — множество дуг графа G. Граф G (I, U) имеет следующие свойства [c.195]
Множество дуг [/графа G (I, U) неоднородно и состоит из дуг типа [c.195]
Положим длины дуг графа РВЗ равными затратам на оплату [c.32]
ДУГА ГРАФА [ar ] — см. Граф. [c.97]
Вычислительные алгоритмы представляются взвешенными ориентированными ациклическими графами [72] (рис. 1.39). Вершины таких графов соответствуют некоторым частям алгоритма, в дальнейшем называемыми операциями. Дуги графа, соединяющие вершины, означают наличие информационной зависимости между соответствующими операциями алгоритма — результат выполнения одной операции является аргументом для другой. Веса вершин пропорциональны времени выполнения соответствующих операций — будем измерять их числом некоторым элементарных операций, содержащихся в соответствующей данной вершине операции. Под элементарной операцией можно понимать, например, арифметическую операцию (сложения/умножения) или один такт процессора. Дуги графа алгоритма также являются взвешенными, и их вес равен объему (например, в байтах) передаваемой по этой дуге информации. [c.137]
Каждую дугу графа будем представлять в виде упорядоченной пары номеров вершин (i,j), которые эта дуга соединяет. [c.137]
Каждая из дуг графа обозначает пересылку одного трехмерного массива, поэтому вес всех дуг равен N слов, и если положить, что 1 слово = 4 байтам, то вес дуг равен 64N Бт. [c.164]
Проведен численный анализ зависимости ускорения, достигаемого при распараллеливании явного метода решения системы нелинейных динамических систем от параметров ВС — числа процессоров и скорости работы каналов обмена данными. Так как веса всех вершин и дуг графа этого алгоритма суть величины одного порядка по N (где N есть размерность задачи), то увеличение N, в отличие от рассмотренных выше алгоритмов линейной алгебры, на ускорение никак не влияет. По причине больших объемов передаваемых данных при выполнении алгоритма ускорение больше 1 достигается только на очень высоких (относительно производительности процессоров) скоростях каналов, что делает рассмотренный метод мало пригодным к выполнению на большинстве реальных [c.166]
Однако наибольший интерес представляет второй способ его задания — графический. Зададим на плоскости множество Nn виде кружков и множество А в виде линий, соединяющих эти кружки. Тогда тот же граф будет иметь вид, представленный на рис. 4.8. Ребро считается ориентированным, если порядок следования вершин в соответствующей паре (ij) A строго задан. Такие пары называются дугами графа и изображаются на рисунках стрелками. Граф G (N, А) называется ориентированным, если все элементы его множества А — дуги. [c.121]
При параллельном соединении блоков в подсистему цель ее формируется одновременным достижением целей входящих в нее блоков, которые состоят с целью подсистемы в определенных отношениях. Связями между целями элементарных блоков и целью подсистемы при этом служат дуги графа целей R. Цель Ц»Г1 достигается, если достигнуты » 1Пз (рис.15). [c.59]
Какая бы процедура не использовалась, в результате должен быть получен список концептов (вершин знакового графа), список отношений причинности (дуг графа) и список значений отношений [c.182]
Задача генерации всех возможных сценариев может быть решена различными методами. Все они, так или иначе, сводятся к перебору дуг графа, описывающего создавшуюся проблему. Поэтому решение задачи могло бы быть дано и в терминах теории графов. Однако с точки зрения перспектив решения подобных задач для графов со значительно более сложной структурой (например, когда на элементы графа накладываются различные условия) более перспективным может оказаться использование аппарата формальных грамматик. [c.186]
Элементы и множество связей между ними и их признаками могут быть представлены в форме графа, носящего название И—ИЛИ дерева [1]. На нем в виде вершин изображаются структурные элементы, в качестве которых могут быть узлы, детали, части деталей. На этом же графе рядом со структурной вершиной изображаются вершины признаков. Вершины могут быть двух видов И или ИЛИ. На графе они имеют разное обозначение. Дуги графа означают связи между структурными элементами. И—ИЛИ дерево может относиться как к одной конкретной технической системе, так и к целой их совокупности. В последнем случае каждой технической системе соответствует конкретный путь от основания дерева к его вершине. [c.128]
Поскольку подсистема бухгалтерского учета представляет собой взаимосвязанный набор комплексов учетных задач, сгруппированных по признаку однородности массивов информации в отдельные блоки, все задачи могут быть представлены в виде связного графа, в котором каждая задача является вершиной графа, а дуги графа указывают взаимосвязи задачи, т. е. возможное использование информации одной задачи для решения другой. [c.35]
Как уже отмечалось, классификация адаптивных свойств в целом представляет собой древовидный ориентированный граф. Каждая из вершин этого графа представляет адаптивное свойство того или иного уровня в классификационной иерархии, корень графа — полное множество адаптивных свойств АСУ. Множество дуг графа является отображением разбиения отдельных подмножеств адаптивных свойств на подмножества адаптивных свойств иерархически более низкого уровня (ранга) или элементарные адаптивные свойства, т. е. такие, которые не являются совокупностью двух или более других адаптивных свойств. Отметим, что ранг элементарных адаптивных свойств равен 1. [c.33]
Vi=0,5 V2=0,3 V3=0,2. В результате определены веса всех дуг графа, изображенного на рис. 26. [c.37]
Примерами графа являются 1) сети железных дорог (вершины — ж.-д. узлы, а рёбра — рельсовые пути) 2) схемы шоссейных дорог. Часто рёбрам графа приписывается ориентация (направление), т. е. указывается начальная п конечная вершины рёбер, тогда элементы из U наз. дугами графа, а сам граф [c.111]
На рис. 4.4. точки принятия решения о выборе стратегии или наборе базовых стратегий соответствуют вершинам графа, а условия работы предприятия соответствуют движению вдоль дуг графа. Каждой точке принятия решения поставлен в соответствие некоторый набор стратегий, рекомендуемых предприятию. Если это не так, то для принятия решения требуется дополнительная информация об условиях работы предприятия, что соответствует обязательному переходу к следующей вершине графа. [c.110]
Определим веса дуг графа как алгебраическую сумму относительных приростов (потерь) критериев системы при переходе от управления ип к [c.129]
Дуги графа помечены степенями принадлежности ц. которые ассоциируются с возможностью переходов из одного состояния в другое. Граф строится на основании экспертных данных и отображает реальные представления о смене графических изображений. Функцию принадлежности любому из состояний будем [c.182]
Функция создания и корректировки когнитивной карты (в). Для реализации необходимо 1) задать вершины графа, представляющие собой элементы когнитивной карты 2) задать дуги графа, представляющие собой отношения между элементами когнитивной карты 3) задать текущие значения параметров вершин графа 4) представить и отобразить на экране дисплея созданный ориентированный граф 5) сохранить данные построенного графа в файле на жестком диске для последующего использования построенной когнитивной карты. [c.221]
Чтобы произвести оценку риска банкротства количественно и качественно, необходимо произвести агрегирование данных, собранных в рамках древовидной иерархии при этом агрегирование совершается по направлению дуг графа иерархии. [c.35]
Легко представить эту задачу с помощью графа. Населенные пункты представляются вершинами графа, а шоссейные дороги—дугами, которые их соединяют. Станция технического обслуживания должна быть расположена на одной из дуг графа. [c.265]
Улицы представляются дугами некоторого графа. Задача почтальона заключается в том, чтобы найти маршрут обхода всех дуг графа минимальной длины. [c.265]
Поток на графе — это совокупность однородных объектов, пересылаемых из одной вершины в. другую по его дугам. Если вершины р и q соединены дугой а — (р, q), то поток из р в щ обозначается f(p, q). Таким образом, поток — это некоторая функция, заданная на дугах графа. [c.266]
Алгоритм поиска Кратчайшего пути В ходе выполнения алгоритма окрашивают вершины и дуги графа и вычисляют величины d(x), равные кратчайшему пути из вершины s в вершину х, включающему только окрашенные вершины. [c.270]
Функциональная модель подсистемы, цель которой формируется объединением нескольких целей нижележащего уровня (параллельное соединение блоков), может быть образована установлением функциональных связей между векторами, характеризующими каждую из исходных целей, с векторами, отражающими цель подсистемы, (см. рис. 13). В качестве таких связей используют отношения между указанными целями, т. е. дуги (г) графа целей, так как множества этих дуг являются отношениями условий достижения целей верхнего уровня и условием Я. Например, цель Z(«j достигается, [c.35]
Наиболее рациональным приемом анализа и расчета параметров корреляционной связи с помощью группировки является построение так называемой корреляционной решетки (табл. 8.3). Это таблица, в которой изучаемая совокупность сгруппирована одновременно по обоим признакам, связь между которыми изучается (двумерное распределение). Число групп по признакам может быть как равным, так и неравным. Если наибольшие числа частот каждой строки и каждого столбца располагаются на первой диагонали (в табл. 8.3 эти цифры подчеркнуты), связь является прямой и близкой к линейной если наибольшие числа частот располагаются вдоль второй диагонали (в табл. 8.3 эти цифры также подчеркнуты), связь обратная, линейная. Если частоты во всех клетках таблицы примерно равны, связи нет если наибольшие числа расположены по дуге, связь криволинейная. В табл. 8.3 кроме частот приведены строки и графы [c.255]
В простейшем случае рассмотрение может быть сведено к системе из двух элементов проект и организатор. Подобная схема приведена на рис. 2.1, вершины графа изображены прямоугольниками, а дуги помечены названиями денежных потоков. Под «проектом» в данной схеме понимается достаточно сложная система, которая включает в себя производственные мощности проекта, трудовые ресурсы, поставщиков, подрядные организации, покупателей продукции проекта и другие элементы, которые необходимы для организации производства и сбыта продукции проекта. Все эти элементы удобно объединить в одну систему, называемую «проект», и уже для нее производить оценку денежных потоков. [c.41]
Внутри любого узла (кроме виртуального узла parent) происходит обработка транзакта, определяемая спецификой его типа. Дуги графа представляют собой пути миграции транзактов по графу модели и имеют направленность. Возможны ситуации, когда один узел имеет несколько выходов, тогда путь транзакта определяется условиями, заданными в узле-источнике. [c.165]
Для определения понятия ациклической схемы БД введем граф соединений на множестве отношений (SI, S2. Sk). Вершинами графа соединений являются имена существующих отношений SI, S2. Sk. Дуга графа существует, если в структуре отношений Si и Sj имеются общие атрибуты. Обозначим их для определенности через A(i j) и назовем весом дуги. Путь на графе соединений называется А-путем, если атрибут А содержится в структуре каждого отношения, лежащего на пути. В графе соединений требуется, чтобы для каждой пары отношений Si, Sj с общим атрибутом A(i,j) существовал A(i j)-nyrb между Si и Sj. [c.93]
Теория графов. Основные понятия и виды графов
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Теория графов
В переводе с греческого граф — «пишу», «описываю». В современном мире граф описывает отношения. И наоборот: любое отношение можно описать в виде графа.
Теория графов — обширный раздел дискретной математики, в котором системно изучают свойства графов.
Теория графов широко применяется в решении экономических и управленческих задач, в программировании, химии, конструировании и изучении электрических цепей, коммуникации, психологии, социологии, лингвистике и в других областях.
Для чего строят графы: чтобы отобразить отношения на множествах. По сути, графы помогают визуально представить всяческие сложные взаимодействия: аэропорты и рейсы между ними, разные отделы в компании, молекулы в веществе.
Давайте на примере.
На множестве A зададим отношение знакомства между людьми из этого множества. Строим граф из точек и связок. Связки будут связывать пары людей, знакомых между собой.
Число знакомых у одних людей может отличаться от числа знакомых у других людей, некоторые могут вовсе не быть знакомы (такие элементы будут точками, не соединёнными ни с какой другой). Так получился граф:
В данном случае точки — это вершины графа, а связки — рёбра графа.
Теория графов не учитывает конкретную природу множеств A и B. Существует большое количество разных задач, при решении которых можно временно забыть о содержании множеств и их элементов. Эта специфика не отражается на ходе решения задачи.
Например, вопрос в задаче стоит так: можно ли из точки A добраться до точки E, если двигаться только по соединяющим точки линиям. Когда задача решена, мы получаем решение, верное для любого содержания, которое можно смоделировать в виде графа.
Не удивительно, что теория графов — один из самых востребованных инструментов при создании искусственного интеллекта: ведь искусственный интеллект может обсудить с человеком вопросы отношений, географии или музыки, решения различных задач.
Графом называется система объектов произвольной природы (вершин) и связок (ребер), соединяющих некоторые пары этих объектов.
Пусть V — (непустое) множество вершин, элементы v ∈ V — вершины. Граф G = G(V) с множеством вершин V есть некоторое семейство пар вида: e = (a, b), где a, b ∈ V, указывающих, какие вершины остаются соединёнными. Каждая пара e = (a, b) — ребро графа. Множество U — множество ребер e графа. Вершины a и b — концевые точки ребра e.
Широкое применение теории графов в компьютерных науках и информационных технологиях можно объяснить понятием графа как структуры данных. В компьютерных науках и информационных технологиях граф можно описать, как нелинейную структуру данных.
Линейные структуры данных особенны тем, что связывают элементы отношениями по типу «простого соседства». Линейными структурами данных можно назвать массивы, таблицы, списки, очереди, стеки, строки. В нелинейных структурах данных элементы располагаются на различных уровнях иерархии и подразделяются на три вида: исходные, порожденные и подобные.
Курсы обучения математике помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Основные понятия теории графов
Граф — это геометрическая фигура, которая состоит из точек и линий, которые их соединяют. Точки называют вершинами графа, а линии — ребрами.
Лемма о рукопожатиях
В любом графе сумма степеней всех вершин равна удвоенному числу ребер.
Доказательство леммы о рукопожатиях
Если ребро соединяет две различные вершины графа, то при подсчете суммы степеней вершин мы учтем это ребро дважды.
Если же ребро является петлей — при подсчете суммы степеней вершин мы также учтем его дважды (по определению степени вершины).
Из леммы о рукопожатиях следует: в любом графе число вершин нечетной степени — четно.
Пример 1. В классе 30 человек. Может ли быть так, что у 9 из них есть 3 друга в этом классе, у 11 — 4 друга, а у 10 — 5 друзей? Учесть, что дружбы взаимные.
Если бы это было возможно, то можно было бы нарисовать граф с 30 вершинами, 9 из которых имели бы степень 3, 11 — со степенью 4, 10 — со степенью 5. Однако у такого графа 19 нечетных вершин, что противоречит следствию из леммы о рукопожатиях.
Пример 2. Каждый из 102 учеников одной школы знаком не менее чем с 68 другими. Доказать, что среди них найдутся четверо ребят с одинаковым числом знакомых.
Сначала предположим противоположное. Тогда для каждого числа от 68 до 101 есть не более трех человек с таким числом знакомых. С другой стороны, у нас есть ровно 34 натуральных числа, начиная с 68 и заканчивая 101, а 102 = 34 * 3.
Это значит, что для каждого числа от 68 до 101 есть ровно три человека, имеющих такое число знакомых. Но тогда количество людей, имеющих нечетное число знакомых, нечетно. Противоречие.
Путь и цепь в графе
Путем или цепью в графе называют конечную последовательность вершин, в которой каждая вершина (кроме последней) соединена со следующей в последовательности вершин ребром.
Циклом называют путь, в котором первая и последняя вершины совпадают.
Путь или цикл называют простым, если ребра в нем не повторяются.
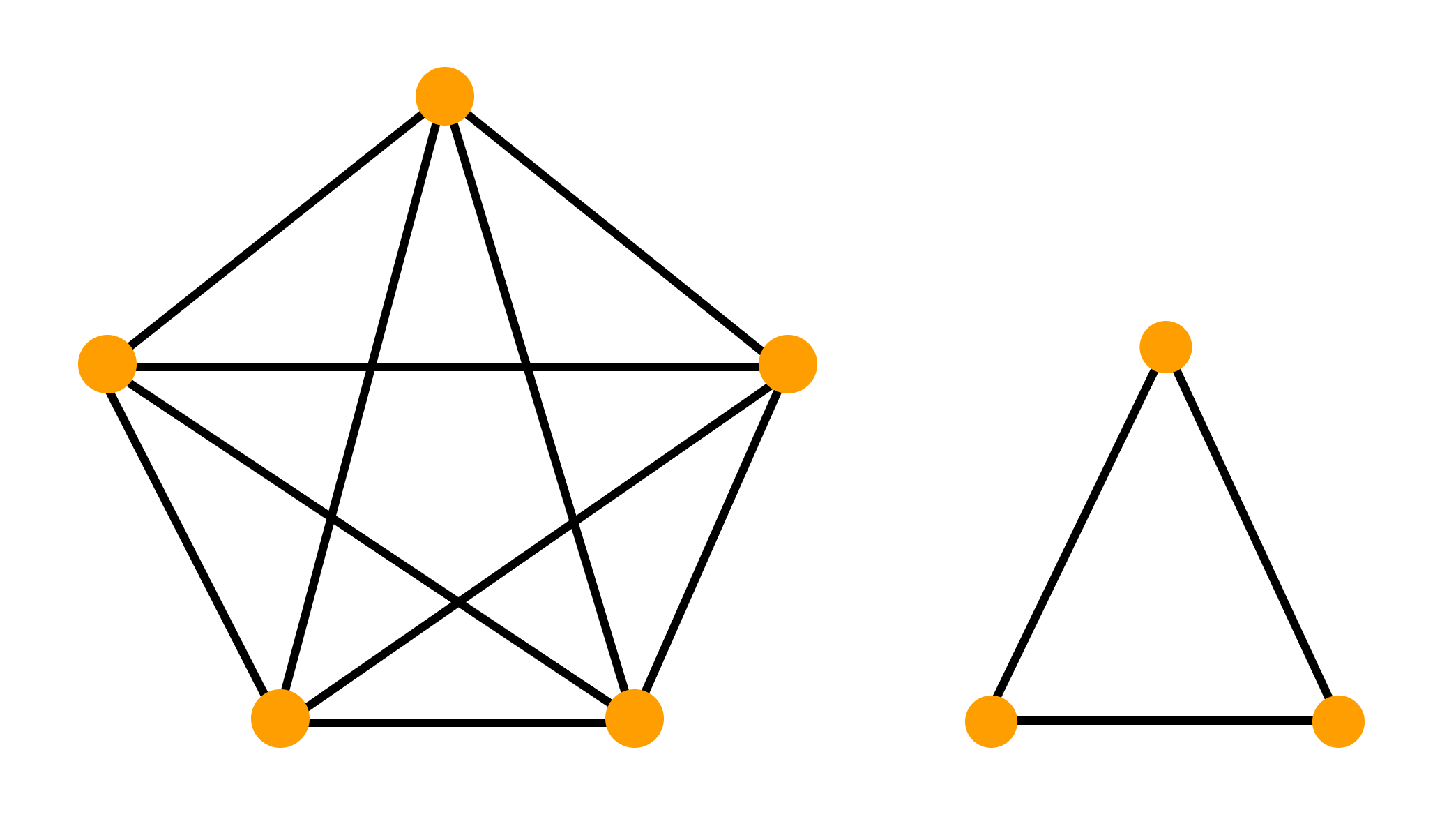
Если в графе любые две вершины соединены путем, то такой граф называется связным.
Можно рассмотреть такое подмножество вершин графа, что каждые две вершины этого подмножества соединены путем, а никакая другая вершина не соединена ни с какой вершиной этого подмножества.
Каждое такое подмножество, вместе со всеми ребрами исходного графа, соединяющими вершины этого подмножества, называется компонентой связности.
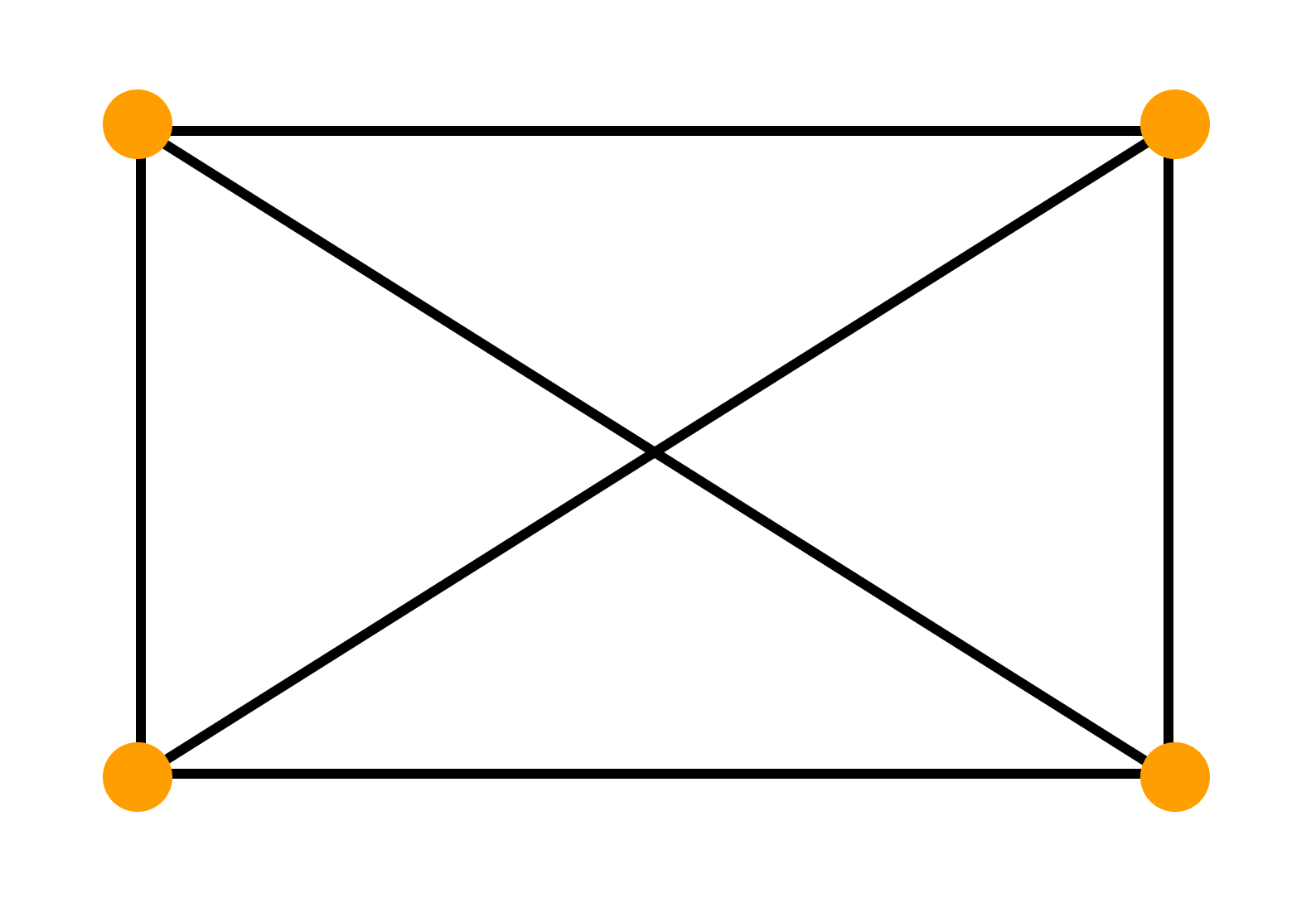
Один и тот же граф можно нарисовать разными способами. Вот, например, два изображения одного и того же графа, которые различаются кривизной:
Два графа называются изоморфными, если у них поровну вершин. При этом вершины каждого графа можно занумеровать числами так, чтобы вершины первого графа были соединены ребром тогда и только тогда, когда соединены ребром соответствующие занумерованные теми же числами вершины второго графа.
Граф H, множество вершин V’ которого является подмножеством вершин V данного графа G и множество рёбер которого является подмножеством рёбер графа G соединяющими вершины из V’ называется подграфом графа G.
Визуализация графовых моделей
Визуализация — это процесс преобразования больших и сложных видов абстрактной информации в интуитивно-понятную визуальную форму. Другими словами, когда мы рисуем то, что нам непонятно — и сразу все встает на свои места.
Графы — и есть помощники в этом деле. Они помогают представить любую информацию, которую можно промоделировать в виде объектов и связей между ними.
Граф можно нарисовать на плоскости или в трехмерном пространстве. Его можно изобразить целиком, частично или иерархически.
Изобразительное соглашение — одно из основных правил, которому должно удовлетворять изображение графа, чтобы быть допустимым. Например, при изображении блок-схемы программы можно использовать соглашение о том, что все вершины должны изображаться прямоугольниками, а дуги — ломаными линиями с вертикальными и горизонтальными звеньями. При этом, конкретный вид соглашения может быть достаточно сложен и включать много деталей.
Виды изобразительных соглашений:
Виды графов
Виды графов можно определять по тому, как их построили или по свойствам вершин или ребер.
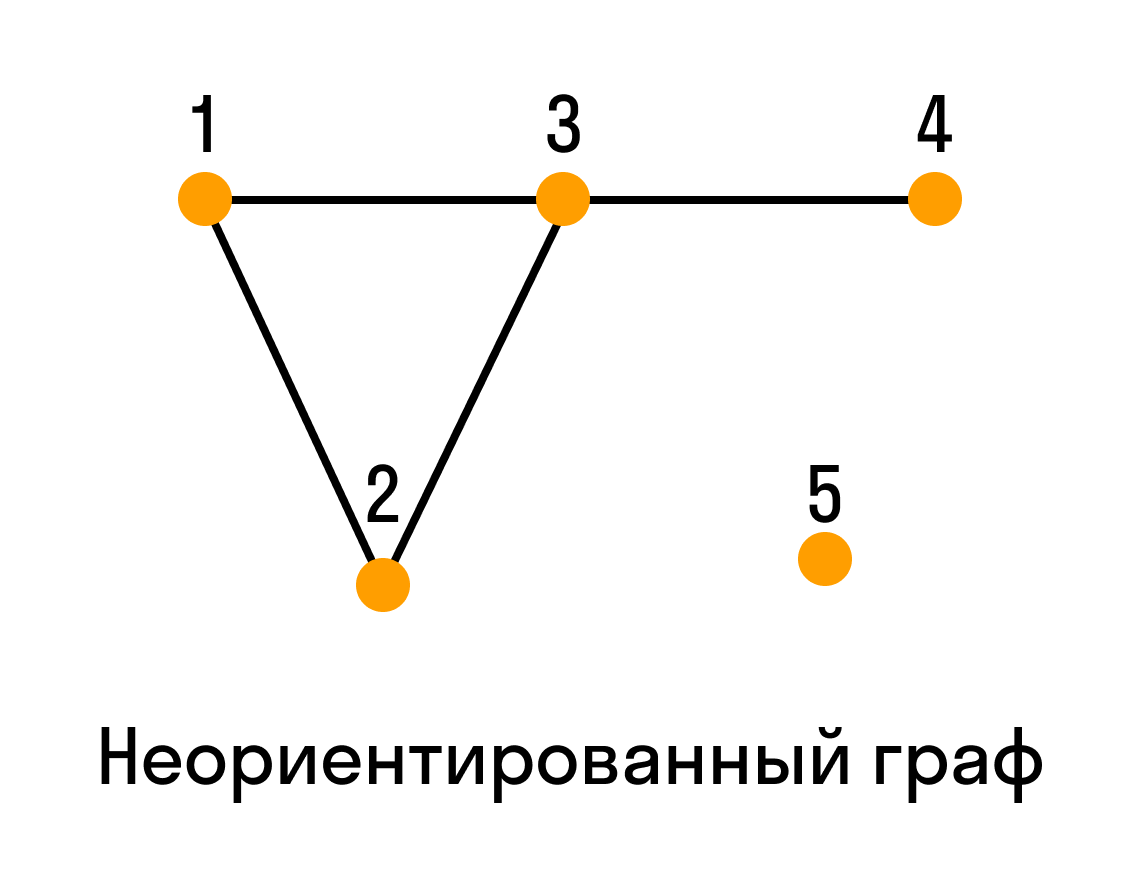
Ориентированные и неориентированные графы
Графы, в которых все ребра являются звеньями, то есть порядок двух концов ребра графа не существенен, называются неориентированными.
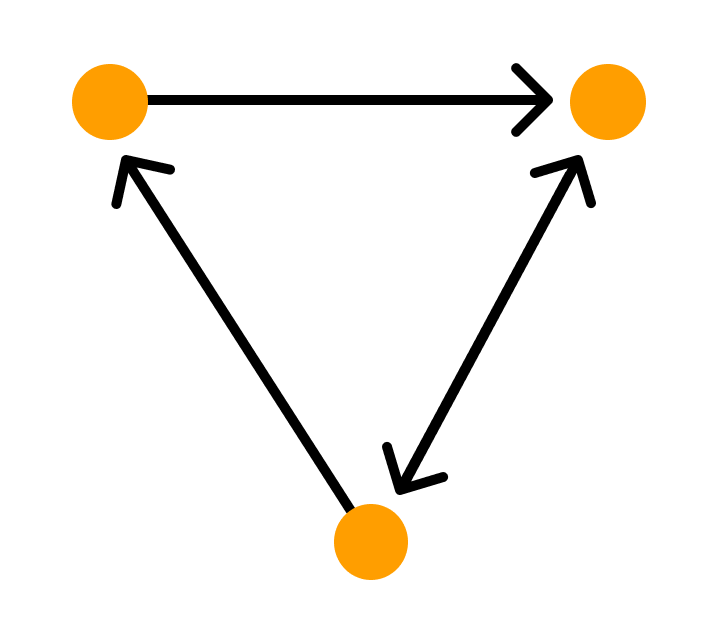
Графы, в которых все ребра являются дугами, то есть порядок двух концов ребра графа существенен, называются ориентированными графами или орграфами.
Неориентированный граф можно представить в виде ориентированного графа, если каждое его звено заменить на две дуги с противоположным направлением.
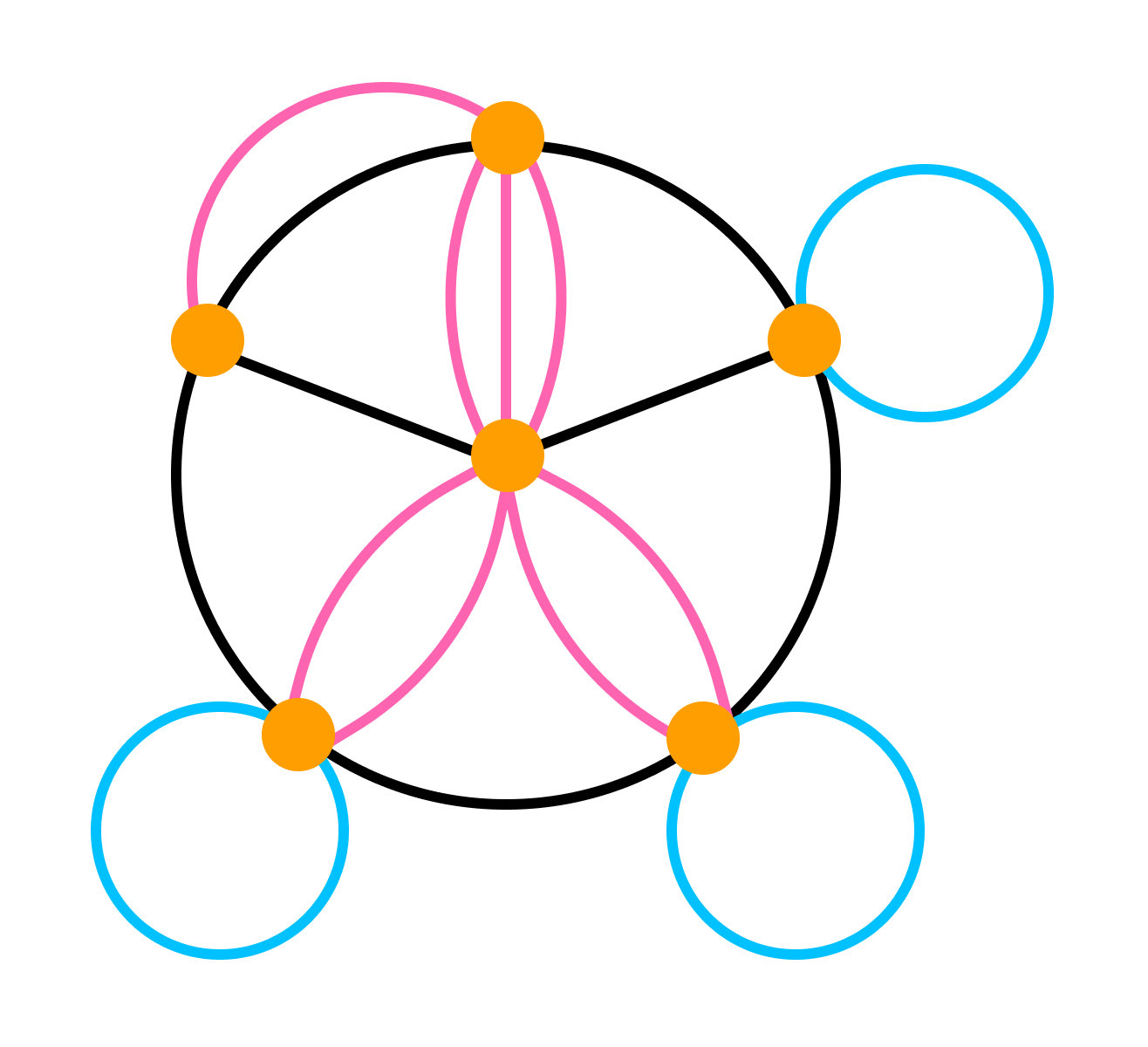
Графы с петлями, смешанные графы, пустые графы, мультиграфы, обыкновенные графы, полные графы
Если граф содержит петли — это обстоятельство важно озвучивать и добавлять к основной характеристике графа уточнение «с петлями». Если граф не содержит петель, то добавляют «без петель».
Смешанным называют граф, в котором есть ребра хотя бы двух из упомянутых трех разновидностей (звенья, дуги, петли).
Пустой граф — это тот, что состоит только из голых вершин.
Мультиграфом — такой граф, в котором пары вершин соединены более, чем одним ребром. То есть есть кратные рёбра, но нет петель.
Граф без дуг, то есть неориентированный, без петель и кратных ребер называется обыкновенным.
Граф называют полным, если он содержит все возможные для этого типа рёбра при неизменном множестве вершин. Так, в полном обыкновенном графе каждая пара различных вершин соединена ровно одним звеном.
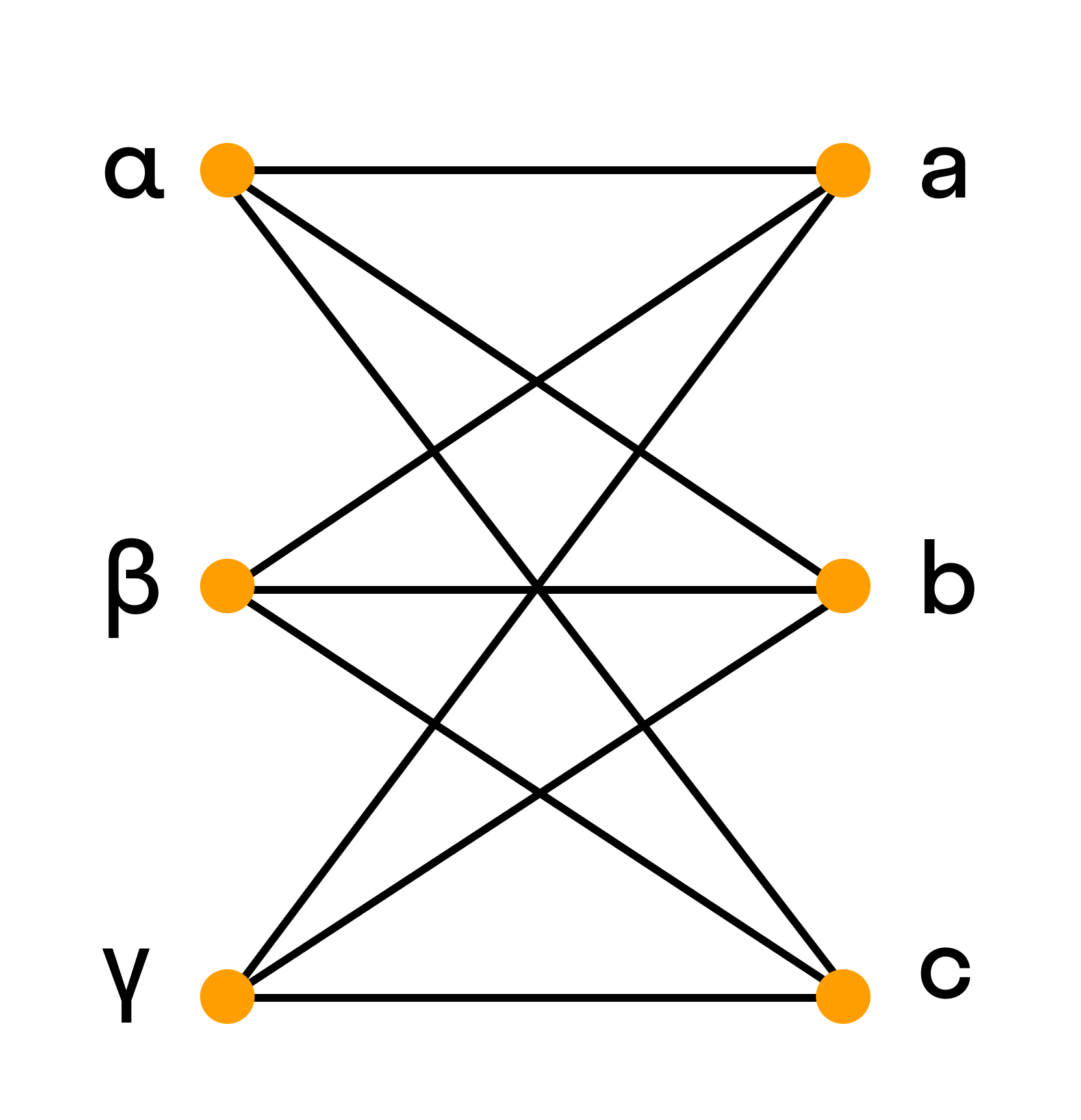
Двудольный граф
Граф называется двудольным, если множество его вершин можно разбить на два подмножества так, чтобы никакое ребро не соединяло вершины одного и того же подмножества.
Например, полный двудольный граф состоит из двух множеств вершин и из всевозможных звеньев, которые соединяют вершины одного множества с вершинами другого множества.
Эйлеров граф
Эйлеров граф отличен тем, что в нем можно обойти все вершины и при этом пройти одно ребро только один раз. В нём каждая вершина должна иметь только чётное число рёбер.
Пример. Является ли полный граф с одинаковым числом n рёбер, которым инцидентна каждая вершина, эйлеровым графом?
Регулярный граф
Регулярным графом называется связный граф, все вершины которого имеют одинаковую степень k.
Число вершин регулярного графа k-й степени не может быть меньше k + 1. У регулярного графа нечётной степени может быть лишь чётное число вершин.
Пример. Построить регулярный граф, в котором самый короткий цикл имеет длину 4.
Чтобы длина цикла соответствовала заданному условию, нужно чтобы число вершин графа было кратно четырем. Если число вершин равно четырём — получится регулярный граф, в котором самый короткий цикл имеет длину 3.
Увеличим число вершин до восьми (следующее кратное четырем число). Соединим вершины ребрами так, чтобы степени вершин были равны трём. Получаем следующий граф, удовлетворяющий условиям задачи:
Гамильтонов граф
Гамильтоновым графом называется граф, содержащий гамильтонов цикл.
Гамильтоновым циклом называется простой цикл, который проходит через все вершины рассматриваемого графа.
Говоря проще, гамильтонов граф — это такой граф, в котором можно обойти все вершины, и каждая вершина при обходе повторяется лишь один раз.
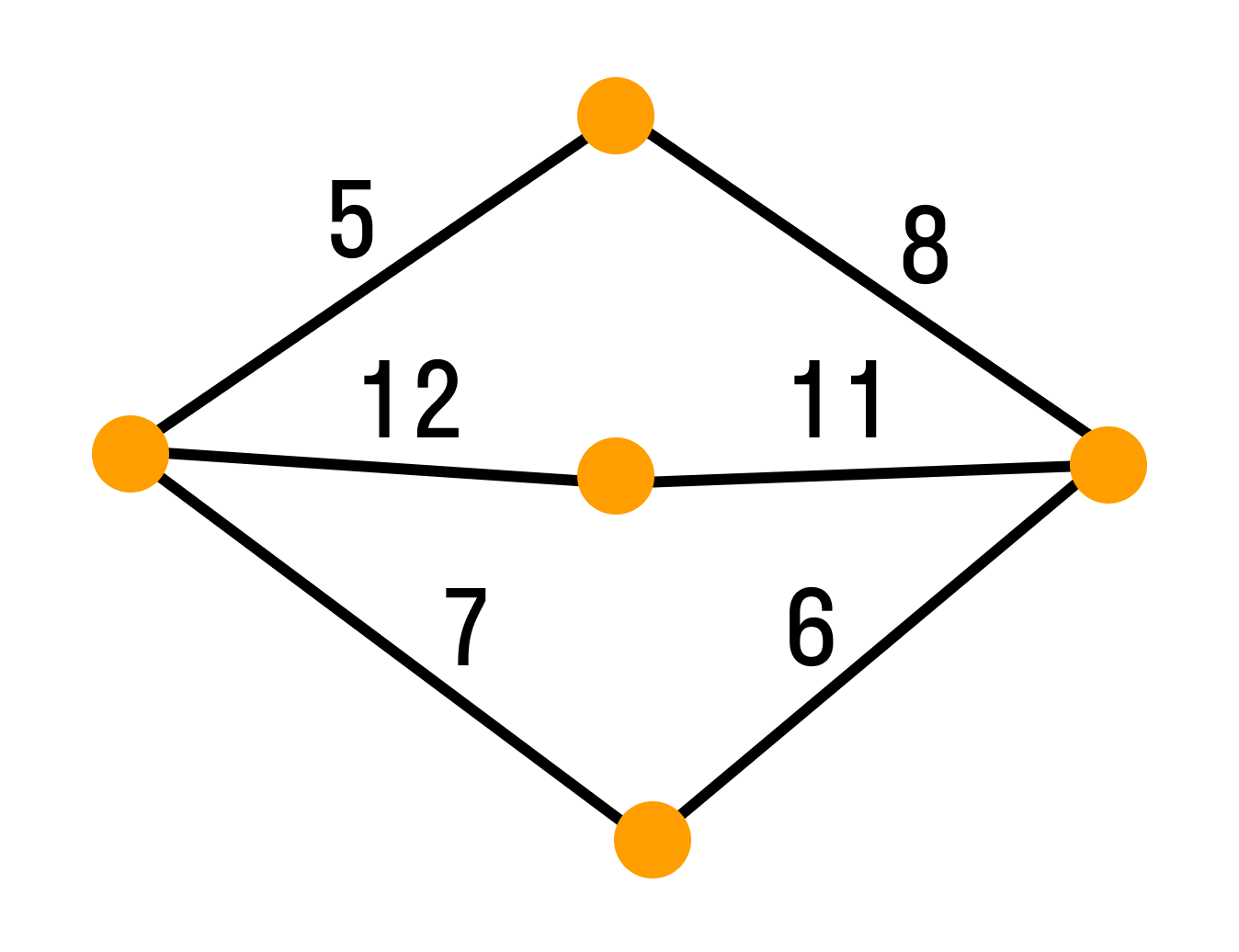
Взвешенный граф
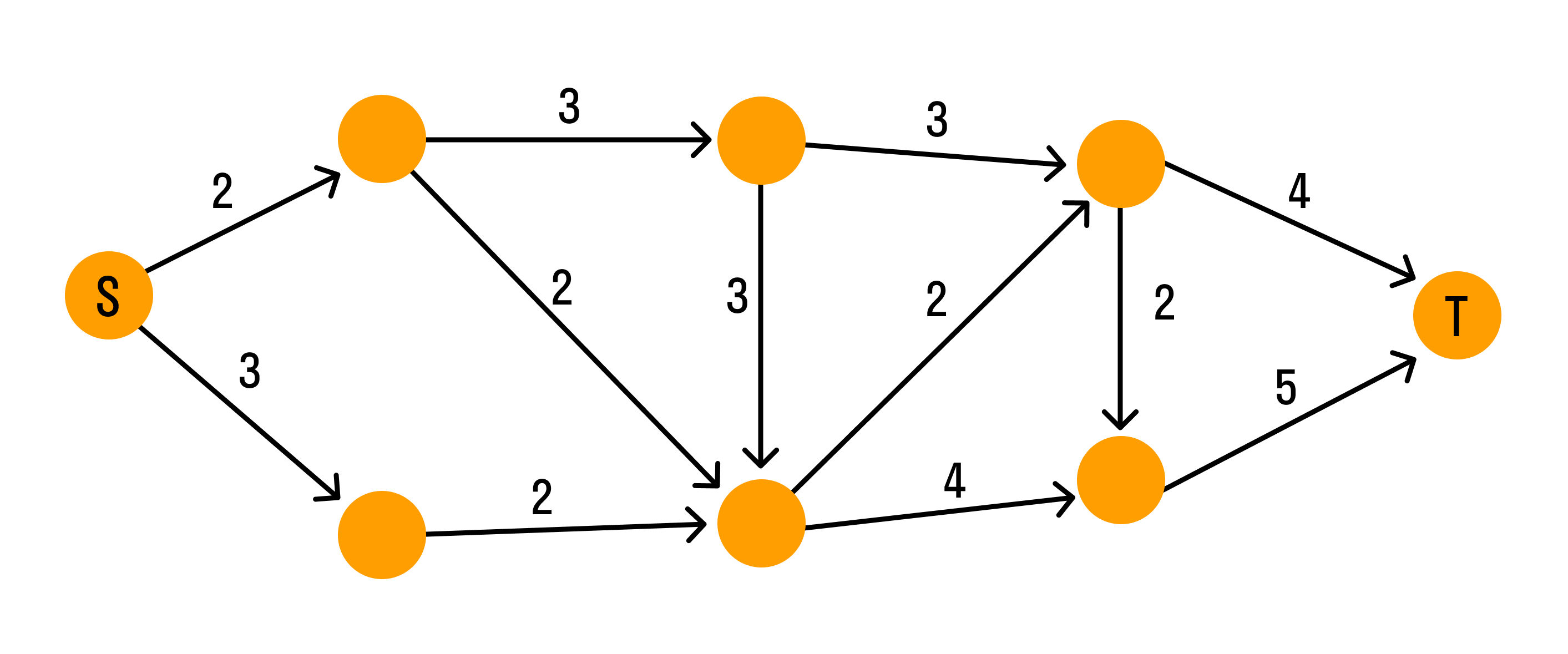
Взвешенным графом называется граф, вершинам и/или ребрам которого присвоены «весы» — обычно некоторые числа. Пример взвешенного графа — транспортная сеть, в которой ребрам присвоены весы: они показывают стоимость перевозки груза по ребру и пропускные способности дуг.
Графы-деревья
Деревом называется связный граф без циклов. Любые две вершины дерева соединены лишь одним маршрутом.
Приведенное соотношение выражает критическое значение числа рёбер дерева, так как, если мы присоединим к дереву ещё одно ребро — будет создан цикл. А если уберем одно ребро, то граф-дерево разделится на две компоненты. Граф, состоящий из компонент дерева, называется лесом.
Определение дерева
Деревом называется связный граф, который не содержит циклов.
Таким образом, в дереве невозможно вернуться в исходную вершину, перемещаясь по ребрам и не проходя по одному ребру два или более раз.
Циклом называется замкнутый путь, который не проходит дважды через одну и ту же вершину.
Простым путем называется путь, в котором никакое ребро не встречается дважды.
Легко проверить, что дерево — это граф, в котором любые две вершины соединены ровно одним простым путем. Если выкинуть любое ребро из дерева, то граф станет несвязным. Поэтому:
Дерево — минимальный по числу рёбер связный граф.
Висячей вершиной называется вершина, из которой выходит ровно одно ребро.
Определения дерева:
Очень часто в дереве выделяется одна вершина, которая называется корнем дерева. Дерево с выделенным корнем называют корневым или подвешенным деревом. Пример: генеалогическое дерево.
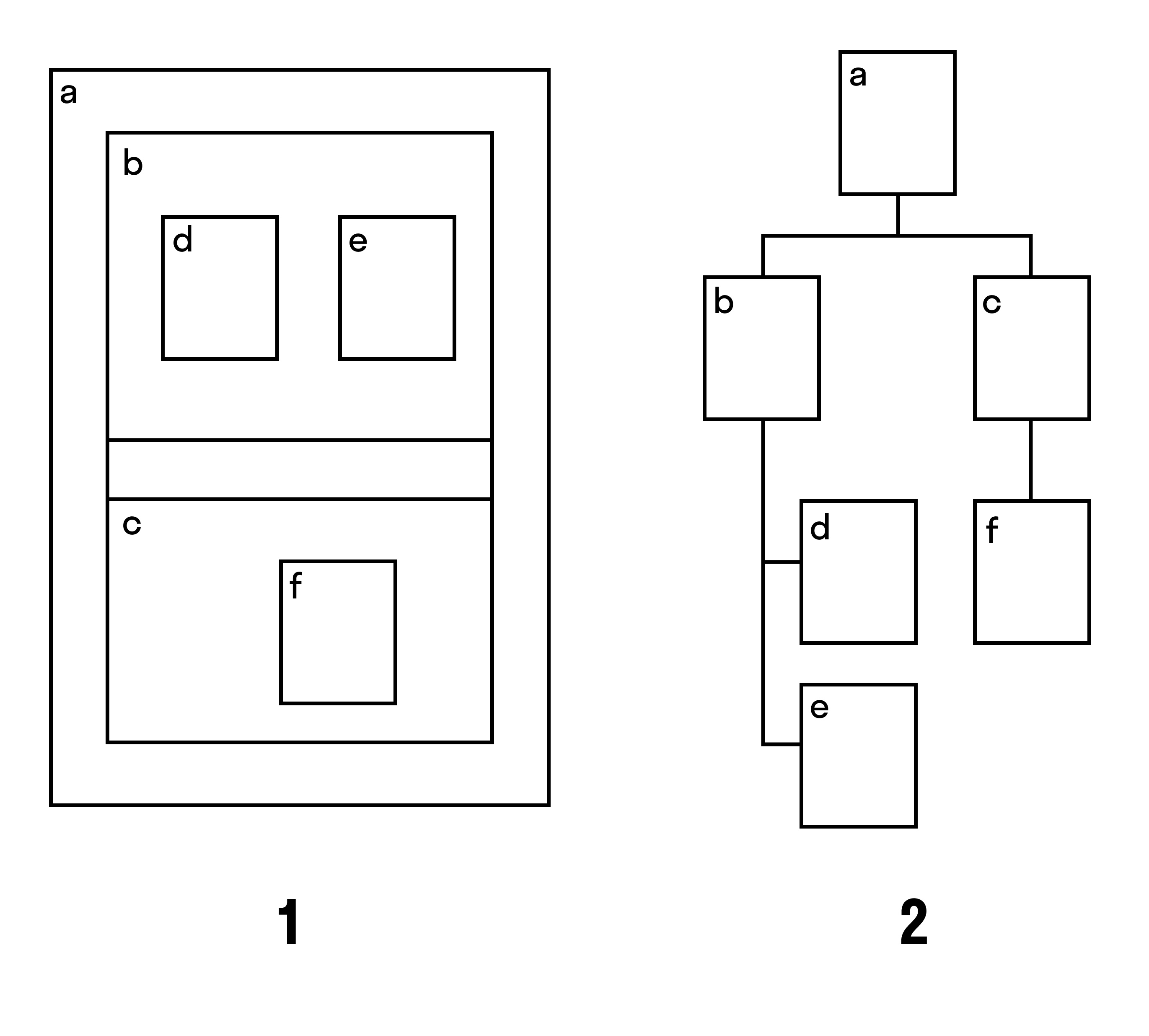
Когда изображают деревья, то часто применяют дополнительные соглашения, эстетические критерии и ограничения.
Например, при соглашении включения (рис. 1) вершины корневого дерева изображают прямоугольниками, а соглашение — опрокидывания (рис. 2) подобно классическому соглашению нисходящего плоского изображения корневого дерева. Вот так могут выглядеть разные изображения одного дерева:
Теоремы дерева и их доказательства
В дереве с более чем одной вершиной есть висячая вершина.
Доказательство первой теоремы:
Пойдем из какой-нибудь вершины по ребрам. Так как в дереве нет циклов, то мы не вернемся в вершину, в которой уже побывали. Если у каждой вершины степень больше 1, то найдется ребро, по которому можно уйти из неё после того, как мы пришли в нее.
Но поскольку количество вершин в дереве конечно, когда-нибудь мы остановимся в некоторой вершине. Противоречие. Значит, когда-нибудь мы дойдём в висячую вершину. Если же начать идти из неё, то мы найдём вторую висячую вершину.
В дереве число вершин на 1 больше числа ребер.
Доказательство второй теоремы:
Докажем по индукции по количеству вершин в дереве n. Если в дерево одна вершина, то факт верен. Предположим, что для всех n