Что такое дроби и проценты
Проценты
Процент это один из интересных и часто применяемых на практике инструментов. Проценты частично или полностью применяются в любой науке, на любой работе и даже в повседневном общении. Человек, хорошо разбирающийся в процентах, создаёт впечатление умного и образованного. В данном уроке мы узнаем, что такое процент и какие действия можно с ним выполнять.
Что такое процент?
В повседневной жизни дроби встречаются наиболее часто. Они даже получили свои названия: половина, треть и четверть соответственно.
Но есть ещё одна дробь, которая тоже встречается часто. Это дробь (одна сотая). Данная дробь получила название процент.
Дробь означает, что нечто разделено на сто частей и от этих ста частей взята одна часть. Значит процентом является одна сотая часть.
Процентом является одна сотая часть
Например, 
от одного метра уже составляет 2 сантиметра. В этот раз один метр разделили на сто частей и взяли оттуда не одну, а две части. А две части из ста составляют два сантиметра. Значит два процента от одного метра составляет 2 сантиметра.
Еще пример, 
Проценты встречались настолько часто, что люди заменили дробь 
Эта запись читается как «один процент». Она заменяет собой дробь 

1% = 
Как найти процент?
Принцип нахождения процента такой же, как и обычное нахождение дроби от числа. Чтобы найти процент от чего-либо, нужно это чего-либо разделить на 100 частей и полученное число умножить на нужный процент.
Например, найти 2% от 10 см.
А как решать подобные задания мы уже знаем. Это обычное нахождение дроби от числа. Чтобы найти дробь от числа, нужно это число разделить на знаменатель дроби, и полученный результат умножить на числитель дроби.
Итак, делим число 10 на знаменатель дроби
Получили 0,1. Теперь 0,1 умножаем на числитель дроби
Получили ответ 0,2. Значит 2% от 10 см составляет 0,2 см. А если перевести 0,2 сантиметра в миллиметры, то получим 2 миллиметра:
Значит 2% от 10 см составляют 2 мм.
Пример 2. Найти 50% от 300 рублей.
Чтобы найти 50% от 300 рублей, нужно эти 300 рублей разделить на 100, и полученный результат умножить на 50.
Итак, делим 300 рублей на 100
Теперь полученный результат умножаем на 50
Значит 50% от 300 рублей составляет 150 рублей.
Если на первых порах сложно привыкнуть к записи со значком %, можно заменять эту запись на обычную дробную запись.
В принципе, ничего сложного здесь нет. Если возникают сложности, советуем остановиться и заново изучить дроби и как их можно применять.
Пример 3. Швейная фабрика выпустила 1200 костюмов. Из них 32% составляют костюмы нового фасона. Сколько костюмов нового фасона выпустила фабрика?
Здесь нужно найти 32% от 1200. Найденное число будет ответом к задаче. Воспользуемся правилом нахождения процента. Разделим 1200 на 100 и полученный результат умножим на искомый процент, т.е. на 32
Ответ: 384 костюмов нового фасона выпустила фабрика.
Второй способ нахождения процента
Второй способ нахождения процента намного проще и удобнее. Он заключается в том, что число от которого ищется процент сразу умножит на нужный процент, выраженный в виде десятичной дроби.
Например, решим предыдущую задачу этим способом. Найти 50% от 300 рублей.
Запись 50% заменяет собой запись 

Теперь для нахождения 50% от 300, достаточно будет умножить число 300 на десятичную дробь 0,5
Кстати, по этому же принципу работает механизм нахождения процента на калькуляторах. Чтобы найти процент с помощью калькулятора, нужно ввести в калькулятор число от которого ищется процент, затем нажать клавишу умножения и ввести искомый процент. Затем нажать клавишу процента %
Нахождения числа по его проценту
Зная процент от числа, можно узнать всё число. Например, предприятие выплатило нам 60000 рублей за работу, и это составляет 2% от общей прибыли, полученной предприятием. Зная свою долю, и сколько процентов она составляет, мы можем узнать общую прибыль.
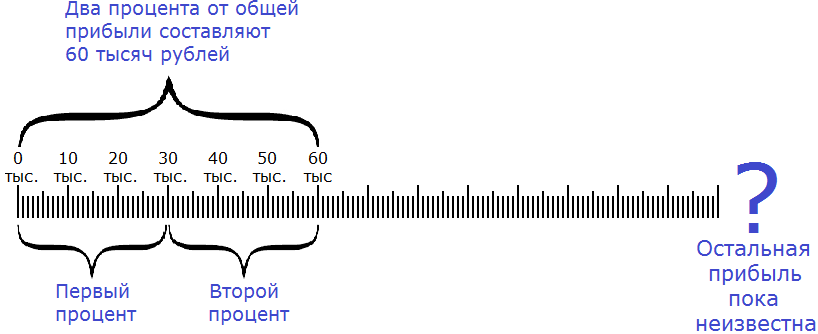
Сначала нужно узнать сколько рублей составляет один процент. Как это сделать? Попробуйте догадаться внимательно изучив следующий рисунок:
Если два процента от общей прибыли составляют 60 тысяч рублей, то нетрудно догадаться, что один процент составляет 30 тысяч рублей. А чтобы получить эти 30 тысяч рублей, нужно 60 тысяч разделить на 2
Мы нашли один процент от общей прибыли, т.е. 
30 000 × 100 = 3 000 000
Мы нашли общую прибыль. Она составляет три миллиона.
Попробуем сформировать правило нахождения числа по его проценту.
Чтобы найти число по его проценту, нужно известное число разделить на данный процент, и полученный результат умножить на 100.
Пример 2. Число 35 это 7% от какого-то неизвестного числа. Найти это неизвестное число.
Читаем первую часть правила:
Чтобы найти число по его проценту, нужно известное число разделить на данный процент
У нас известное число это 35, а данный процент это 7. Разделим 35 на 7
Читаем вторую часть правила:
и полученный результат умножить на 100
У нас полученный результат это число 5. Умножим 5 на 100
500 это неизвестное число, которое требовалось найти. Можно сделать проверку. Для этого находим 7% от 500. Если мы всё сделали правильно, то должны получить 35
Получили 35. Значит задача была решена правильно.
Принцип нахождения числа по его проценту такой же, как и обычное нахождение целого числа по его дроби. Если проценты на первых порах смущают и сбивают с толку, то запись с процентом можно заменять на дробную запись.
Например, предыдущая задача может быть изложена так: число 35 это 
В будущем мы будем решать задачи на проценты, часть из которых будут сложными. Чтобы на первых порах не усложнять обучение, достаточно уметь находить процент от числа, и число по проценту.
1.1.3 Дроби, проценты, рациональные числа
Видеоурок: Десятичные дроби и проценты
Лекция: Дроби, проценты, рациональные числа
Итак, что же все-таки такое дроби?
Дробь может быть смешанной, то есть иметь и дробную и целую часть.
Обыкновенная дробь может иметь произвольный числитель и знаменатель.
Например, 1/5, 4/7, 7/11 и т.д.
Десятичная дробь в знаменателе всегда имеет числа 10, 100, 1000, 10000 и т.д.
Например, 1/10 = 0,1; 6/100 = 0,06 и т.д.
Над дробями можно производить те же математические действия, что и над целыми числами:
1. Сложение и вычитание дробей
Нельзя складывать и вычитать те дроби, что имеют разные знаменатели. Чтобы произвести данное действие следует привести слагаемые к общему знаменателю. Для этого следует найти наименьшее общее кратное. Например,
Для данных дробей наименьшим числом, которое делится на один и второй знаменатель, является число 30.
Чтобы привести обе дроби к знаменателю 30, следует найти дополнительный множитель. Чтобы в первой дроби получить знаменатель 30, её следует умножить на 6. Чтобы во второй дроби получить знаменатель 30, её следует умножить на 5. Чтобы значение дроби не изменилось, на данные числа умножаем и числитель, и знаменатель. В результате этого получаем:
Чтобы сложить или вычесть числа с одинаковыми знаменателями, следует в результате оставить знаменатель 30, а числители сложить:
2. Умножение дробей
При умножении двух дробей, следует перемножить их числители, после чего перемножить знаменатели, и записать результат:
При делении двух дробей необходимо вторую дробь перевернуть и выполнить действие умножение:
4. Сокращение дробей
Если числитель и знаменатель кратный некоторому одинаковому числу, то такую дробь можно сократить, разделив и числитель, и знаменатель на данное число.
В первоначальной дроби и числитель, и знаменатель делится на число 3, поэтому всю дробь можно сократить на данное число.
5. Сравнение дробей
При сравнении дробей необходимо пользоваться несколькими правилами:
— Если происходит сравнение дробей, которые имеют одинаковый знаменатель, но разный числитель, то больше будет та дробь, у которой больше числитель. То есть данное сравнение сводится к сравнению числителей.
— Если дроби имеют одинаковые числители, но различные знаменатели, то необходимо сравнить знаменатели. Та дробь будет больше, чей знаменатель меньше.
— Если дроби имеют разные и числители, и знаменатели, то их необходимо привести к общему знаменателю.
Теперь сравнение сводится к первому правилу. Больше та дробь, у которой больше знаменатель:

Любое число, которое составляет одну сотую часть от некоторого целого, называют одним процентом.
Чтобы перевести некоторую дробь в процентную запись, её следует перевести в десятичную дробь, а после этого умножить на 100%.
Проценты используют в трех основных случаях:
1. Если необходимо найти некоторый процент от числа. Представьте себе, что ежемесячно вы получаете 10% от заработной платы Ваших родителей. Однако, если Вы не знаете математики, то не сможете рассчитать, чему будут равны Ваши ежемесячные доходы. Итак, это сделать достаточно просто.
Представим, что Ваши родители ежемесячно получают 100000 рублей. Чтобы найти сумму, которую Вы должны получать ежемесячно, необходимо прибыль родителей разделить на 100 и умножить на 10%, которые Вы должны получить:
100000 : 100 * 10 = 10000 (рублей).
2. Если Вам нужно узнать, какую сумму получают Ваши родители ежемесячно, если Вы знаете, что они Вам дают 6000 рублей, а это, в свою очередь, 3%, то данное действие с процентами называется нахождением числа по его проценту. Для этого необходимо получаемую сумму умножить на 100 и разделить на Ваши проценты:
6000 * 100 : 3 = 200000 (рублей).
3. Если Вы в течение дня выпиваете 1 л воды, а Вам, например, необходимо выпить 2 литра воды, то Вы с легкостью можете найти значение процента выпитой воды. Для этого необходимо 1 л разделить на 2 л и умножить на 100%.
Основные сведения о понятии процента в математике
Что называют процентами
В 1 метре 100 сантиметров, значит, 1 сантиметр — это сотая часть метра.
В 1 центнере 100 килограмм, значит, 1 килограмм — сотая часть центнера.
Сотую часть числа или какой-либо величины называют процентом.
Тогда 1 сантиметр — один процент метра, а 1 килограмм — один процент центнера.
Понятие процент произошло от латинского «per centum», что в переводе означает «на сто, на сотню, сотая».
Идея использования процентов встречается у вавилонян. Они пользовались шестидесятеричными дробями. В их табличках встречаются решения задач на расчет процентов.
Процентами пользовались в Индии. Математики использовали тройное правило для вычисления процентов: вычисляли их с помощью пропорции — равенства двух отношений.
С помощью обыкновенных дробей вида 1/100 вычисления производились в Древнем Риме. Например, взимали налоги на товары, аукционах. И соответствующая мера была известна как сотая доля продаваемых вещей.
Процент — одна сотая часть числа.
Слово «процент» заменяют знаком %.
Например, предложение «Колбасные изделия подорожают на 5%» читают так: «Колбасные изделия подорожают на пять процентов».
Есть несколько версий происхождения этого знака.
Одна из них заключается в том, что знак произошел от итальянского слова cento — сто. Писали как cto. А когда обозначение трансформировалось — буква t стала наклонной чертой — получили современный знак для обозначения процента.
Другая версия происхождения символа % сводится к тому, что знак возник в результате опечатки наборщика текста.
Если 1% = сотой части числа или величины, то все число или величина = 100%.
В слове процент ударение на втором слоге сохраняется в единственном и множественном числе во всех падежах. Читается в том падеже, в котором и числительное, в большинстве случаев.
1 4 = 25 % — одна пятая равна двадцати пяти процентам — в дательном падеже.
Когда зависимым словом выступает числительное, то используют сочетание «несколько процентов (от чего?)…».
Например, «двадцать шесть процентов от пятидесяти».
Если зависимое слово — существительное без количественного значения, то используют фразу «несколько процентов (чего?)…».
Например, «двадцать процентов времени».
Допускают употребление обеих конструкций.
Например, «девять процентов стоимости» и «девять процентов от стоимости».
В современном мире величины часто сравнивают не по разности их значений, а по процентному соотношению, процентам. Но указывают, относительно какой величины вычисляется процент. Проценты упрощают расчеты.
Иногда применяют и гораздо меньшие, тысячные доли — промилле (латинское понятие — «с тысячи»).
Основная связь между десятичными дробями и процентами
Если нужно перевести десятичную дробь в проценты, то ее умножают на 100 и дописывают знак %.
Переведите десятичную дробь 0,98 в проценты.
Чтобы перевести 0,98 в проценты, нужно 0,98 умножить на 100%.
По правилу, когда десятичную дробь умножаем на 100, запятую переносим вправо на 2 знака (по количеству нулей после единицы в числе 100). Получим 98%.
Если нужно совершить обратную операцию — перевести проценты в десятичную дробь, то число делят на 100%.
Переведите 56% в десятичную дробь.
Чтобы перевести проценты в десятичную дробь, нужно число процентов разделить на 100%.
При делении на 100 по правилу отсчитываем в числе количество знаков справа налево, равное количеству нулей, и ставим запятую. Значит, при делении на сто запятую ставим, отсчитав два знака влево от конца записи числа. Получим 0,56.
Перевод процентов в десятичную дробь
Если проценты переводят в десятичную дробь, то делят число процентов на 100.
Запишите в виде десятичной дроби: 2%; 12%.
Для решения задачи используем правило: делим число процентов на 100.
У 100 два нуля после единицы, значит, отсчитываем влево два знака и ставим запятую. В целой части десятичной дроби пишем ноль.
Со вторым числом процентов поступаем аналогично:
Способы нахождения процента
Правило нахождения процентов от числа:
Чтобы найти процент от числа, нужно перевести процент в десятичную дробь и умножить на заданное число.
Действуем по алгоритму:
Чтобы не путаться, можно записать краткое условие:
Правило нахождения числа по его проценту:
Чтобы найти число по его процентам, нужно:
36 составляет 45% числа. Найдите это число.
Запишем краткое условие:
обозначим неизвестное число знаком вопроса. Оно будет составлять сто процентов.
Тогда переводим 45% в десятичную дробь. Для этого делим 45% на 100%. Получим 0,45 — это 1%. И, чтобы найти искомое число, делим 36 на 0,45. Получим искомое число: 80.
Задания для самостоятельного решения
Запишите в виде десятичной дроби: 87%; 3,4%; 243%.
Чтобы перевести проценты в десятичную дробь, нужно число процентов разделить на 100. При делении числа на 100 отсчитываем два знака влево и ставим запятую.
Ответ: 0,87; 0,034 и 2,43.
Запишите десятичные дроби в процентах: 0,54; 0,004; 4,876.
Чтобы перевести десятичную дробь в проценты, умножаем десятичную дробь на 100%. При умножении десятичной дроби на 100 запятую переносим вправо на два знака.
Егору на дом было задано прочитать 32 страниц книги. Он прочитал 8 страниц. Сколько процентов заданных страниц прочитал Егор.
Решим эту задачу двумя способами.
1 способ
2 способ
Запишем краткое условие задачи в таблицу.
Егор прочитал 8 страниц — запишем данные в таблицу в первую строку. Сколько это процентов, мы не знаем, поставим знак вопроса.
Ему нужно прочитать 32 страницы. 32 страницы возьмем за 100%, потому что это все, что ему задали на прочтение. Запишем данные во вторую строку таблицы.
| Прочитал | 8 страниц | ? |
| Нужно прочитать | 32 страницы | 100% |
Узнаем, чему равен 1% всех заданных станиц. Для этого разделим 32 на 100.
32:100=0,32, значит, 1% равен 0,32. Теперь, чтобы найти процент прочитанного Егором, делим 8 страниц на 0,32. Получим:
Ответ: Егор прочитал 25% заданных страниц.
Маша решила три примера, что составляет 15 процентов от заданных на дом. Сколько всего примеров нужно решить Маше?
Запишем краткое условие.
Маша решила 3 примера — это 15%. Все примеры, которые Маше нужно решить — это 100%.
Обозначим все примеры, которые ей нужно решить, знаком вопроса.
Для решения этой задачи воспользуемся алгоритмом нахождения числа по его проценту.
Чтобы найти число примеров, которые нужно решить Маше, делим три на 0,15: 3:0,15=20.
Что такое дроби и проценты
Рассмотрим преобразования дробей, процентов и десятичных дробей.
Перевод процентов в десятичную дробь
Чтобы перевести проценты в десятичную дробь нужно: разделить число на 100 и убрать знак процента «%».
Деление на 100 можно интерпретировать как перенос позиционный запятой на 2 позиции влево.
| Проценты → Десятичные дроби |
|---|
| Переносим позиционную запятую(точку) на 2 позиции влево и убираем знак процента % |
Перевод десятичной дроби в проценты
Чтобы перевести десятичную дробь в проценты нужно: умножить дробь на 100 и добавить знак процента «%».
Умножение на 100 можно интерпретировать как перенос позиционный запятой на 2 позиции вправо.
| Десятичные дроби → Проценты |
|---|
| Переносим позиционную запятую(точку) на 2 позиции вправо и добавляем знак процента % |
Перевод дроби в десятичную дробь
Чтобы перевести дробь в десятичную дробь нужно: разделить числитель на знаменатель.
Пример Преобразовать  в десятичную дробь
в десятичную дробь
Разделим 3 на 4: 3 ÷ 4 = 0.75
Ответ: 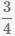
Перевод десятичной дроби в дробь
Пример Преобразовать десятичную дробь 0.45 в дробь
Первое, запишем число в виде дроби, с знаменателем 1

Посчитаем количество знаков после запятой(точки)
и умножим столько раз на 10 числитель и знаменатель.

После выполнения умножения получается дробь в корректной форме
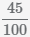
Сократим дробь и получим завершенное преобразование.
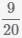
Перевести дроби в проценты
Чтобы перевести дробь в проценты нужно разделить числитель на знаменатель, затем умножить результат на 100 и добавить знак процентов «%».
Пример Преобразовать дробь  в проценты
в проценты
Сначала разделим числитель 3 на знаменатель 4: 3 ÷ 4 = 0.75
Затем умножим полученный результат на 100: 0.75*100=75
Добавим знак процента «%»: 75%
Ответ: 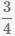
Преобразование процентов в дробь
Чтобы преобразовать проценты в дробь нужно разделить проценты на 100, получим десятичную дробь и следом преобразуем десятичную дробь в обычную дробь.
Пример Преобразовать 60% в дробь.
Преобразуем 60% в десятичную дробь, разделим 60 на 100
запишем 0.6 в виде дроби с знаменателем 1
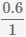
Посчитаем количество знаков после запятой(точки)
и умножим столько раз на 10 числитель и знаменатель.
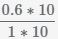
После выполнения умножения получается дробь в корректной форме
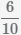
Сократим дробь и получим завершенное преобразование.
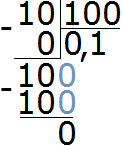














 0.45
0.45 45%
45%