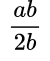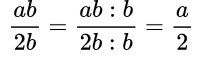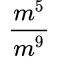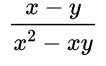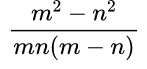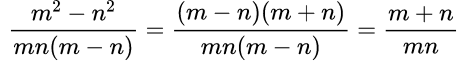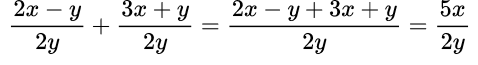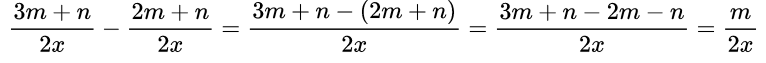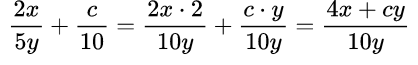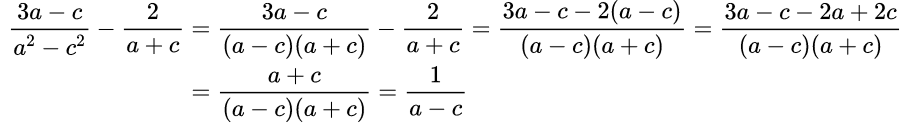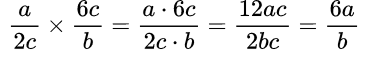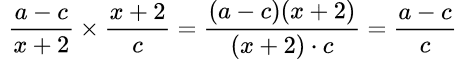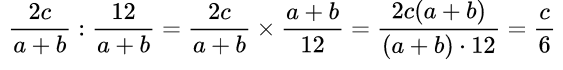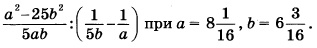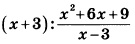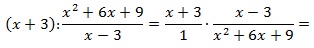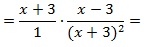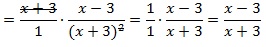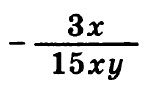Что такое дроби 7 класс алгебра
ОБЫКНОВЕННАЯ ДРОБЬ
Ключевые слова конспекта: дроби, обыкновенная дробь, правильные и неправильные дроби, основное свойство дроби, сравнение дробей, арифметические действия с дробями, нахождение части от целого и целого по его части.
Одна или несколько равных частей единицы называются обыкновенной дробью. Дробь 3/4 означает, что единицу разделили на 4 части и взяли 3 таких части.
Дробь можно рассматривать и как результат деления натуральных чисел. Частное от деления натуральных чисел а и b можно записать в виде дроби a/b — где делимое а — числитель, а делитель b — знаменатель.
Правильная и неправильная дробь
Дробь, в которой числитель меньше знаменателя, называется правильной, а дробь, где числитель больше или равен знаменателю, — неправильной.
Число, состоящее из целой и дробной частей, можно обратить в неправильную дробь. Для этого нужно умножить целую часть на знаменатель и к произведению прибавить числитель данной дроби. Полученная сумма будет числителем дроби, а знаменателем остается знаменатель дробной части.
Из любой неправильной дроби можно выделить целую часть. Для этого нужно разделить с остатком числитель на знаменатель. Частное от деления — это целая часть, остаток — это числитель, делитель — это знаменатель.
Основное свойство дроби
Определение. Основное свойство дроби: если числитель и знаменатель дроби умножить или разделить на одно и то же отличное от нуля число, то получится дробь, равная данной.
Основное свойство дроби используют при сокращении дробей. Деление числителя и знаменателя на их общий делитель, отличный от единицы, называют сокращением дробей.
Сравнение дробей
Чтобы сравнить дроби с разными числителями и знаменателями, нужно:
Чтобы привести дроби к наименьшему общему знаменателю, нужно:
Арифметические действия с обыкновенными дробями
Сложение и вычитание дробей
При сложении (вычитании) дробей с одинаковыми знаменателями к числителю первой дроби прибавляют числитель второй дроби (из числителя первой вычитают числитель второй) и оставляют тот же знаменатель. Полученную дробь, если возможно, сокращают и выделяют целую часть.
При сложении (вычитании) дробей с разными знаменателями нужно предварительно привести эти дроби к наименьшему общему знаменателю, затем сложить (вычесть) полученные дроби, используя правило сложения (вычитания) дробей с одинаковыми знаменателями.
Особенно надо быть внимательным при сложении (вычитании) с участием смешанных чисел!
Общий случай сложения (вычитания) дробей.
Умножение дробей
Деление дробей
Два числа называются взаимно обратными, если их произведение равно 1, то есть дроби вида a/b и b/a являются взаимно обратными. Например 1/3 и 3. Чтобы разделить одну дробь на другую, нужно делимое умножить на число, обратное к делителю.
При делении чисел, состоящих из целой и дробной части, нужно предварительно представить их в виде неправильной дроби.
Нахождение части от целого (дроби от числа)
Чтобы найти часть от целого, нужно число, соответствующее целому, разделить на знаменатель дроби, выражающей эту часть, и результат умножить на числитель той же дроби.
Задача нахождения части от целого по существу является задачей нахождения дроби от числа. Чтобы найти дробь (часть) от числа, необходимо число умножить на эту дробь.
Нахождение целого по его части (числа по его дроби)
Чтобы найти целое по его части, нужно число, соответствующее этой части, разделить на числитель дроби, выражающей эту часть, и результат умножить на знаменатель той же дроби.
Задача нахождения целого по его части по существу является задачей нахождения числа по его дроби. Чтобы найти число по его дроби, необходимо данное значение разделить на эту дробь.
Это конспект по теме «Обыкновенная дробь». Выберите дальнейшие действия:
Алгебраические дроби
теория по математике 📈 алгебраические выражения
Любая обыкновенная дробь называется алгебраической дробью, так как она представляет собой деление, записанное с помощью дробной черты. В алгебраической дроби могут встречаться не только числа, но и буквенные выражения.
Примеры алгебраических дробей:
Для алгебраических дробей применяются правила, аналогичные обыкновенным дробям.
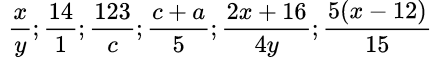
Сокращение алгебраической дроби
Сократить алгебраическую дробь – это значит разделить числитель и знаменатель на одно и то же выражение, на их общий множитель (одночлен, его степень или многочлен) – применяется основное свойство дроби. Причем и числитель, и знаменатель должны содержать множители.
Пример №1. Сократим дробь: 
В числителе и знаменателе дроби мы видим переменную b, на которую и разделим каждую часть дроби:
Промежуточные действия можно не записывать, а выполнять устно.
Пример №2. Сократим дробь: 
Здесь содержатся степени с одинаковым основанием, поэтому, необходимо помнить еще и правило деления степеней с одинаковым основанием (основание остается прежним, а показатели степеней вычитаем). Сократим дробь на меньшую степень – на m 5 :
Пример №3. Сократим дробь: 
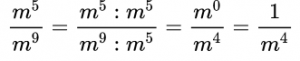
В каждой части дроби содержатся разные многочлены, поэтому сократить пока дробь мы не можем, так как нет множителей. Значит, по возможности, мы должны найти выражение, которое можно разложить на множители, это знаменатель, так как можем вынести за скобки общий множитель х(х – у). Только потом мы можем сократить дробь на одно и то же выражение – многочлен (х – у).
Пример №4. Сократим дробь: 
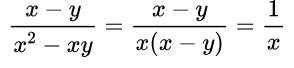
Здесь мы видим, что в числителе многочлен, а в знаменателе произведение одночленов и многочлена, причем многочлены различны. Значит, надо сделать так, чтобы числитель и знаменатель содержали одинаковые множители. Числитель можно разложить на множители по формуле разности квадратов, то есть m 2 – n 2 =(m–n)(m+n), затем сократить дробь на одно и то же выражение (m–n).
Сложение и вычитание алгебраических дробей с одинаковым знаменателем
При сложении и вычитании алгебраических дробей с одинаковыми знаменателями знаменатель остается прежним, а числители складывают или вычитают (из числителя первой вычитают числитель второй дроби).
Пример №5. Выполним сложение дробей: 
Здесь одинаковые знаменатели, поэтому записываем его, а числители складываем: при сложении видим подобные слагаемые, которые приводим и получаем в числителе 5х.
Пример №6. Выполним вычитание дробей: 
В знаменатель записываем 2х, а из числителя первой дроби вычитаем числитель второй дроби, при этом не забываем вычитаемое взять в скобки, если оно является многочленом. Затем раскрываем скобки, помня о том, что необходимо поменять знаки на противоположные, так как перед ними стоит знак «минус». Затем приводим подобные слагаемые и получаем новый числитель.
Сложение и вычитание алгебраических дробей с разными знаменателями
Чтобы сложить или вычесть дроби с разными знаменателями, необходимо:
Пример №7. Выполнить сложение дробей: 
Чтобы найти общий знаменатель, надо найти для чисел 5 и 10 наименьшее общее кратное (наименьшее число, которое делится и на 5, и на 10), это число 10. В первом знаменателе есть еще множитель – переменная у, поэтому также берем у для общего знаменателя. Таким образом, у нас есть два множителя 10 и у, это и есть наш общий знаменатель.
Теперь находим дополнительный множитель к каждой дроби. Для этого общий знаменатель 10у делим на первый знаменатель 5у, получим 2, значит, умножаем на 2 первый числитель 2х. Для второй дроби 10у делим на 10, получаем у, умножаем на него числитель второй дроби – с. Получаем в числителе 4х+су.
Пример №8. Выполнить вычитание дробей: 
Здесь знаменатели дробей различные многочлены, поэтому надо рассмотреть каждый. Первый знаменатель – это формула сокращенного умножения, по ней можно разложить на множители данный многочлен а 2 – с 2 =(а–с)(а+с). Второй знаменатель представляет собой простой многочлен, который нельзя разложить на множители. Составим новый знаменатель, состоящий из разных выражений – это (а–с)(а+с).
Находим дополнительные множители: к первой дроби дополнительного множителя нет, так как новый общий знаменатель – это полностью знаменатель первой дроби. А ко второй дроби это будет выражение (а – с). Поэтому умножаем числитель 2 на (а – с).
Приводим подобные слагаемые, а полученную дробь сокращаем на выражение (а+с).
Умножение алгебраических дробей
Чтобы перемножить алгебраические дроби, надо числитель перемножить с числителем, а знаменатель со знаменателем. При необходимости выполнить сокращение алгебраической дроби, используя правило.
Пример №9. Выполнить умножение дробей:
Здесь перемножаем числители и знаменатели, полученную дробь сокращаем на 2с.
Пример №10. Выполнить умножение дробей: 
Здесь в числителях и знаменателях — многочлены. Поэтому при записи умножения обязательно заключаем их в скобки. При этом мы видим, что числитель и знаменатель содержат одинаковые множители – многочлены (х+2), поэтому можно сократить дробь на этот многочлен.
Деление алгебраических дробей
Чтобы разделить одну алгебраическую дробь на другую, надо первую дробь умножить на дробь, обратную второй (то есть умножить на дробь, у которой числитель равен знаменателю второй дроби, а знаменатель числителю второй дроби). Далее – выполнить умножение дробей по уже известному алгоритму.
Пример №11. Выполнить деление дробей:
Здесь выполним деление по алгоритму: перейдем от деления к умножению на дробь, обратную делителю. Сократим полученную дробь на выражение (a+b) и на 2.
Найдите значение выражения:
Упрощение заданного выражения нужно начать с преобразований в скобках. Здесь следует привести дроби к общему знаменателю:
теперь переходим от деления дробей к их умножению: 
затем 1) сокращаем дроби на 5ab; 2) в числителе первой дроби раскладываем выражение, используя формулу сокращенного умножения для разности квадратов:
сокращаем выражение на (a–5b): 
Представим числовые значения для a и b в виде неправильных дробей (для удобства вычислений): 
Подставим полученные значения в выражение и найдем конечный результат: 
Ответ: 39
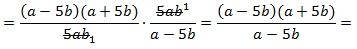
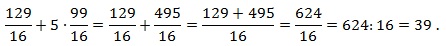
pазбирался: Даниил Романович | обсудить разбор | оценить
Найдите значение выражения при x = 12:
Выполним тождественные преобразования выражения, чтобы упростить его. 1-й шаг – переход от деления дробей к их умножению:
далее в знаменателе второй дроби сворачиваем выражение по формуле сокращенного умножения (используем ф-лу для квадрата суммы):
теперь сокращаем выражение (в числителе первой дроби и в знаменателе второй) и приходим к окончательно упрощенному виду:
Подставляем числовое значение для х в полученное выражение и находим результат:
Ответ: 0,6
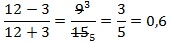
pазбирался: Даниил Романович | обсудить разбор | оценить
Найдите значение выражения
В первую очередь в заданиях такого типа необходимо упростить выражение, а затем подставить числа. Приведем выражение к общему знаменателю — это b, для этого умножим первое слагаемое на b, после этого получим в числителе:
Приведем подобные слагаемые — это 9b² и — 9b², в числителе остается 5a. Запишем конечную дробь:
Вычислим её значение, подставив числа из условия:
pазбирался: Даниил Романович | обсудить разбор | оценить
Найдите значение выражения:
Итак, в данном задании при вычитании дробей нам необходимо привести их к общему знаменателю. Общий знаменатель — это 15 x y, для этого необходимо первую дробь домножить на 5 y — и числитель и знаменатель, естественно:
Далее, после того как дроби приведены к общему знаменателю, можно производить вычисления. Вычислим числитель:
5 y — (3 x + 5 y) = 5 y — 3 x — 5 y = — 3 x
Тогда дробь примет вид:
Выполнив простые сокращения числителя и знаменателя на 3 и на x, получим: — 1/5 y
Подставим значение y = 0,5: — 1 / (5 • 0,5) = — 1 / 2,5 = — 0,4
pазбирался: Даниил Романович | обсудить разбор | оценить
Действия с дробями 7 класс, повторение, сравнение, сокращение, решение уравнений
В начале первой четверти семиклассники на уроках математики активно повторяют все действия, как с обыкновенными, так и с десятичными дробями. И делают они это не просто так.
В 7 классе по программе обучения начинается алгебра. Дроби будут состоять уже из алгебраических выражений, многочленов. Все действия с такими уже > дробями основываются на умении решать обыкновенные дроби в пятом шестом классе.
Дроби повторение 7 класс
Повторение начинается с самых простых примеров на все арифметические действия с обыкновенными дробями. Не забываем, что там где знаменатели разные следует найти общий, и только потом выполнять действия.
Сравнение дробей 7 класс
Для того, чтобы научиться сравнивать дроби, нужно узнать несколько способов по их сравнению, и выбрать для себя более понятный и удобный.
Основные правила сравнения дробей:
В первом правиле мы сравниваем только числители, так как знаменатели равны. Мы уже говорили, что знамен.-это общее количество долей, а числитель показывает сколько их взято из общего, следовательно, чем больше долей взято, тем и дробь соответственно больше.
При одинаковых числ-х сравнивают только знамен. Чем он меньше, тем больше дробь. Разберемся, почему так. К примеру разделите 10 на 5 и 10 на 2, очевидно, что второе частное больше первого. Поэтому, если сравнить 10/5 и 10/2, то 10/2 будет больше.
В десятичных дробях мы сравниваем их соответствующие целые части и дробные. Если первые равны, то мы сравниваем десятые, сотые и т.д. Поэтому для сравнения мы должны уравнивать количество дес.знаков.
Также можно сравнить две обыкн.дроби используя число, которое находится в ряду между ними. Какая из дробей окажется больше этого числа, та и будет большей в примере.
Вот несколько интересных способов, как можно сравнить дроби:
Если от вас требуется сравнить десятичную и обыкновенную дроби, можно перевести одну из них в более удобную для вас. И сравнивать вы уже будите либо обыкновенные, либо десятичные.
Еще один хороший способ, дополнить до единицы. Чем больше нужно добавить дроби, чтобы получить целое, тем она будет меньше.
Можно использовать и перекрестное правило, как в пропорции. Для этого умножаем смотрящие друг на друга числители и знаменатели.
Правила дробей 7 класс
Начиная изучать рациональные дроби в седьмом классе, стоит познакомиться с рядом правил, которым подчиняются действия с ними.
К рациональным дробям применяются те же правила, что и к обыкн-м.
Для выполнения всех арифметических действий, следует знать несколько формул сокращенного умножения:
Эти формулы понадобятся на уроках математики до 11 класса, поэтому их лучше выучить сразу в седьмом.
Действия с дробями 7 класс
Как в пятом и шестом, так же и в седьмом классе, дроби в основном складывают, вычитают, умножают и делят. Есть еще сокращение и сравнение. Рациональные дроби также называют алгебраическими.
Сложение и вычитание.
К примеру, b/3 + c/3. Это сумма рациональных или алгебраических дробей. Решением будет: b+c/3.
Умножение и деление.
Так же как и с обыкновенными дробями, умножать будем числитель на числитель, и знам. на знаменатель. Очень важно обратить внимание на то, что вы умножаете многочлены, поэтому каждый числитель и знаменатель лучше взять в скобки. Так вы сможете избежать ненужных ошибок.
И деление выполняется в точности также как и в обык.дробях. Первую дробь оставьте на месте без изменений, поменяйте частное на умножение, вторую дробь переверните.
Сложение и вычитание дробей 7 класс
Никогда не начинайте выполнять действия не упростив выражения. Выполните все возможные преобразования и пример решится намного легче и быстрее. Также числители второй и последующих дробей при сложении и вычитании стоит взять в скобки. Очень часто возникают ошибки только из-за одного неправильно поставленного знака. Будьте внимательны.
Если перед скобкой стоит >, раскрываем ее, не меняя знаки внутри. Если >, то все меняем на противоположные.
Все намного проще, если знам. одинаковые. С разными нужно немного подумать.
В примере два знам. 15а и 3. Нам нужно найти общий. В этом случае проще домножить 3 так, чтобы получить 15а. Для этого 3 умножаем на 5а. Но чтобы действие было верным, применяем основное свойство дроби, и на 5а умножим еще и числитель. Далее складываем дроби с один.знам.
Деление и умножение дробей 7 класс
Разберем сразу примеры, так как правила уже обговорены выше.
В примере выше требуется разделить алгебраические дроби, содержащие выражения со степенью. Здесь важно вспомнить, что при сокращении степеней мы вычитаем из большей степени меньшую.
Первую дробь мы оставили без изменений, вторую перевернули, заменив действие на умножение. Теперь ищем, что можно сократить. Сначала смотри на числовые коэффициенты. Сокращаем 7 и 35, 9 и 18. Затем сокращаем буквенную часть.
Для удобства возьмите каждый многочлен в скобки. Мы видим, что сразу можно сократить скобку (7-х). Многие допускают ошибку, считая что (a-b) и (a+b) сократимы, это большая ошибка. Ведь к примеру, 5-2 и 5+2 совершенно разные выражения.
Конечные десятичные дроби 7 класс
Десятичные дроби отличаются друг от друга по количеству знаков (цифр) после запятой. Соответственно своему названию, у конечной десятичной дроби после запятой, конечное число знаков: 5, 0235; 2,3654; 0,12 и т.д.
Любую такую дробь можно перевести обратно в обыкновенную. 2,36 = 2 целых 36/100. Но не каждую обыкновенную можно представить в виде конечной дес.дроби. В таком случае уже получается бесконечная дес.дробь.
Уравнения с дробями 7 класс на примерах с пояснением
Уравнения с дробями можно решить используя пропорцию, или светси решение к этому. Первое уравнение и ему подобные очень просто и быстро решается пропорцией. Используем умножение >.
Бывают и более сложные уравнения, которые нужно преобразовать.
Здесь уже нужно вспомнить правило умножения скобки на число или раскрытие скобок. На число перед скобкой умножаем каждое слагаемое в скобке. Значит 7 умножим и на 2, и на (-х). Далее решаем как обычное линейное уравнение.
В следующем уравнении разберем два способа решения.
Первый вариант решения основывается на избавлении от знаменателей, дабы превратить дробное уравнение в линейное. Для этого умножаем каждое слагаемое на общий для дробей знаменатель. В нашем случае 45.
Сокращаем и получаем линейное уравнение. Раскрываем в нем скобки, находим подобные слагаемые.
Вторым вариантом будет приведение к общему знаменателю в правой части, и сведению решения к пропорции.
Сокращение дробей 7 класс
При сокращении рациональных дробей используем правило сокращения обык.др. Числитель и знаменатель делим на один многочлен.
Запомните, что разные буквенные части мы не сокращаем, только одинаковые.
Дроби, в числ. и знамен. которых стоит выражение (многочлен) тоже сократимы. В таких дробях можно сокращать только одинаковые многочлены. Многочлены разделены между собой умножением.
Также можно использовать формулы сокращ. умножения.