Что такое древовидный граф
Древовидная структура
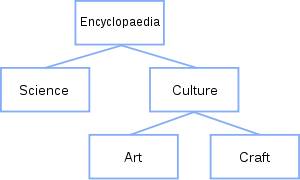
Древовидная структура является одним из способов представления иерархической структуры в графическом виде. Древовидной структурой называется благодаря тому, что граф выглядит как перевернутое дерево. По этой же причине говорят, что корневой узел (корень) находится на самом верху, а листья — внизу.
В теории графов дерево — связанный ациклический граф (иногда его называют направленным ациклическим графом, у которого каждая вершина имеет степень 0 или 1). Ациклический граф без жесткого условия связывания иногда называется лесом (так как он состоит из деревьев).
Из совокупности древовидных структур состоят неоднородные семантические сети.
Содержание
Терминология и свойства
Каждая конечная древовидная структура содержит элемент, не имеющий вышестоящего. Этот элемент называется «корнем» или «корневым узлом». Он может считаться первым (или стартовым) узлом. Обратное утверждение, в общем случае, неверно: бесконечные древовидные структуры могут иметь, а могут и не иметь корневые узлы.
Линии, связывающие элементы называются «ветвями», а сами элементы называются узлами. Узлы без потомков называются «конечными узлами» или «листьями».
Названия связей между узлами именуются по принципу семейных взаимосвязей. На Западе в области информатики, в основном используются только названия членов семьи мужского рода, в русском языке для обозначения узла, напрямую связанного с узлом-родителем и находящимся в иерархии ниже, часто называют «дочерним». В лингвистике (англоязычной, к примеру), напротив, используются названия членов семей женского рода. Это свидетельствует о возврате к соглашению об общепринятых правилах наименования, авторами которого студентки известного американского лингвиста Ноама Хомского. Несмотря на это, в информатике нейтральные названия «родитель» и «дитя» часто заменяются словами «отец» и «сын», кроме того термин «дядя» не менее активно используется для обозначения других узлов, находящихся на том же уровне, что и родитель.
В приведенном выше примере, «энциклопедия» является родителем по отношению к «науке» и «культуре», которые соответственно, являются ее «детьми». «Искусство» и «ремесло» являются братьями по отношению друг к другу и детьми по отношению к «культуре».
Древовидные структуры используются для отображения все видов информации из области таксономии, как например, генеалогическое древо, филогенетическое дерево, грамматическая структура языка (например, в английском языке, хорошим примером является схема S → NP VP, означающая, что предложение (sentence) является именной группой (noun phrase) и глагольной группой (verb phrase), способ логического упорядочивания веб-страниц на сайте и так далее.
В древовидной структуре может быть один и только один путь от одной точки до другой точки.
Древовидные структуры широко используются в информатике (смотри Дерево (структура данных) и Связь (техника)).
Древовидные структуры по видам связей
Межды узлами древовидной структуры могут иметь место различные семантические отношения.
В реальных энциклопедиях (Википедия) все такие ДС существуют в антагонизме, если не продумана система их представления в отдельности и в целом.
Древовидные структуры с различными видами связей
В структуре тематически однородных групп статей Википедии использованы различные виды связей.Первоночально выделены разделы различающиеся по времени появления объектов статей (Неживая природа,Живая природа,Человечество,Техносфера),затем используются связи между структурными уровнями внутри разделов,связи между однородными статьями (родо-видовые),последними в иерархии используется количество статей в группе.
Древовидные структуры образованные различными семантическими отношениями могут быть связаны в пирамидальные структуры.Пирамидальные информационные структуры (ПИС) в Интернете.
Примеры древовидных структур
представление деревьев
Существует множество способов графического представления древовидных структур. В подавляющем большинстве случаев они сводятся к различным вариациям или комбинациям нескольких основных стилей:
Описания некоторых базовых способов можно найти в:
См. также
Дополнительные источники
Ссылки
 Дерево (структура данных) Дерево (структура данных) | |
|---|---|
| Двоичное дерево поиска · Дерево (теория графов) · Древовидная структура | |
| Двоичные деревья | Двоичное дерево · T-дерево |
| Самобалансирующиеся двоичные деревья | АА-дерево · АВЛ-дерево · Красно-чёрное дерево · Расширяющееся дерево · Дерево со штрафами · Декартово дерево · Дерево Фибоначчи |
| B-деревья | B-дерево · 2-3-дерево · B+ дерево · B*-дерево · UB-дерево · 2-3-4 дерево · (a,b)-дерево · Танцующее дерево |
| Префиксные деревья | Суффиксное дерево · Radix tree · Ternary search tree |
| Двоичное разбиение пространства | k-мерное дерево · VP-дерево |
| Недвоичные деревья | Дерево квадрантов · Октодерево · Sparse Voxel Octree · Экспоненциальное дерево · PQ-дерево |
| Разбиение пространства | R-дерево · R+-дерево · R*-дерево · X-дерево · M-дерево · Дерево Фенвика · Дерево отрезков |
| Другие деревья | Куча · TTH · Finger tree · Metric tree · Cover tree · BK-tree · Doubly-chained tree · iDistance · Link-cut tree |
| Алгоритмы | Поиск в ширину · Поиск в глубину · DSW-алгоритм · Алгоритм связующего дерева |
Полезное
Смотреть что такое «Древовидная структура» в других словарях:
древовидная структура — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN tree like structurewindow tree … Справочник технического переводчика
древовидная структура — medžio struktūra statusas T sritis automatika atitikmenys: angl. tree structure vok. baumförmige Struktur, f; Baumstruktur, f rus. древовидная структура, f pranc. arborescence, f; structure arborescente, f … Automatikos terminų žodynas
древовидная структура сети — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN tree structured architecture … Справочник технического переводчика
звеньевая древовидная структура коммутационного поля коммутационного блока (станции) — Структура, при которой в коммутационном поле коммутационного блока (станции) от одного входа к любому выходу имеется не более одного соединительного пути. [ГОСТ 19472 88] Тематики телефонные сети … Справочник технического переводчика
структура — (framework): Логическая структура для классификации и организации сложной информации [3]. Источник: ГОСТ Р ИСО/ТС 18308 2008: Информатизация здоровья. Требования к архитектуре электронного учета здоровья 3.38 стру … Словарь-справочник терминов нормативно-технической документации
Структура коммутационного поля коммутационного блока звеньевая — 113 Источник: ГОСТ 19472 88: Система автоматизированной телефонной связи общегосударственная. Термины и определения … Словарь-справочник терминов нормативно-технической документации
Структура коммутационного поля коммутационной станции звеньевая — 113 Источник: ГОСТ 19472 88: Система автоматизированной телефонной связи общегосударственная. Термины и определения … Словарь-справочник терминов нормативно-технической документации
СТРУКТУРА РУД ДРЕВОВИДНАЯ — син. термина структура руд дендритовая. Геологический словарь: в 2 х томах. М.: Недра. Под редакцией К. Н. Паффенгольца и др.. 1978 … Геологическая энциклопедия
Структура коммутационного поля коммутационного блока звеньевая древовидная — 115 Источник: ГОСТ 19472 88: Система автоматизированной телефонной связи общегосударственная. Термины и определения … Словарь-справочник терминов нормативно-технической документации
Все что нужно знать о древовидных структурах данных
Jul 1, 2018 · 14 min read
Деревья прекрасны. Вот рисунок, который я сделал ребенком
Когда вы впервые учитесь кодировать, общепринято изучать массивы в качестве «основной структуры данных».
В конце концов, вы также изучаете хэш-таблицы. Для получения степени по «Компьютерным наукам» (Computer Science) вам придется походить на занятия по структурам данных, на которых вы узнаете о связанных списках, очередях и стеках. Эти структуры данных называются «линейными», поскольку они имеют логические начало и завершение.
Однако в самом начале и зучения деревьев и графов мы можем оказаться слегка сбитыми с толку. Нам привычно хранить данные линейным способом, а эти две структуры хранят данные совершенно иначе.
Данная статья поможет вам лучше понять древовидные структуры данных и устранить все недоразумения на их счет.
Из этой статьи вы узнаете:
Давайте начнем наше учебное путешествие 🙂
Определения
Когда вы только начинаете изучать программирование, обычно бывает проще понять, как строятся линейные структуры данных, чем более сложные структуры, такие как деревья и графы.
Деревья являются широко известными нелинейными структурами. Они хранят данные не линейным способом, а упорядочивают их иерархически.
Давайте вплотную займемся реальными примерами
Что я имею в виду, когда я говорю иерархически?
Представьте себе генеалогическое древо отношений между поколениями: бабушки и дедушки, родители, дети, братья и сестры и т.д. Мы обычно организуем семейные деревья иерархически.
Мое фамильное дерево
Приведенный рисунок — это мое фамильное древо. Тосико, Акикадзу, Хитоми и Такеми — мои дедушки и бабушки.
Тошиаки и Джулиана — мои родители.
ТК, Юдзи, Бруно и Кайо — дети моих родителей (я и мои братья).
Структура организации — еще один пример иерархии.
Структура компании является примером иерархии
В HTML, объектная модель документа (DOM) представляется в виде дерева.
Объектная модель документа (DOM)
Техническое определение
Дерево представляет собой набор объектов, называемых узлами. Узлы соединены ребрами. Каждый узел содержит значение или данные, и он может иметь или не иметь дочерний узел.
Первый узел дерева называется корнем. Если этот корневой узел соединен с другим узлом, тогда корень является родительским узлом, а связанный с ним узел — дочерним.
Все узлы дерева соединены линиями, называемыми ребрами. Это важная часть деревьев, потому что она управляет связью между узлами.
Листья — это последние узлы на дереве. Это узлы без потомков. Как и в реальных деревьях, здесь имеется корень, ветви и, наконец, листья.
Другими важными понятиями являются высота и глубина.
Высота дерева — это длина самого длинного пути к листу.
Глубина узла — это длина пути к его корню.
Справочник терминов
Бинарные деревья
Теперь рассмотрим особый тип деревьев, называемых бинарными или двоичными деревьями.
“В информатике бинарным (двоичным) деревом называется иерархическая структура данных, в которой каждый узел имеет не более двух потомков (детей). Как правило, первый называется родительским узлом, а дети называются левым и правым наследниками.” — Wikipedia
Рассмотрим пример бинарного дерева.
Давайте закодируем бинарное дерево
Как мы реализуем простое двоичное дерево, которое инициализирует эти три свойства?
Вот наш двоичный класс дерева.
Когда мы создаем наш узел, он не имеет потомков. Просто есть данные узла.
Давайте это проверим:
Перейдем к части вставки. Что нам нужно здесь сделать?
Мы реализуем метод вставки нового узла справа и слева.
Давайте это нарисуем 🙂
Вот программный код:
Еще раз, если текущий узел не имеет левого дочернего элемента, мы просто создаем новый узел и устанавливаем его в качестве left_child текущего узла. Или мы создаем новый узел и помещаем его вместо текущего левого потомка. Назначим этот левый дочерний узел в качестве левого дочернего элемента нового узла.
И мы делаем то же самое, чтобы вставить правый дочерний узел.
Но не полностью. Осталось протестировать.
Давайте построим следующее дерево:
Подытоживая изображенное дерево, заметим:
Таким образом, вот код для нашего дерева следующий:
Теперь нам нужно подумать об обходе дерева.
У нас есть два варианта: поиск в глубину (DFS) и поиск по ширине (BFS).
• Поиск в глубину (Depth-first search, DFS) — один из методов обхода дерева. Стратегия поиска в глубину, как и следует из названия, состоит в том, чтобы идти «вглубь» дерева, насколько это возможно. Алгоритм поиска описывается рекурсивно: перебираем все исходящие из рассматриваемой вершины рёбра. Если ребро ведёт в вершину, которая не была рассмотрена ранее, то запускаем алгоритм от этой нерассмотренной вершины, а после возвращаемся и продолжаем перебирать рёбра. Возврат происходит в том случае, если в рассматриваемой вершине не осталось рёбер, которые ведут в не рассмотренную вершину. Если после завершения алгоритма не все вершины были рассмотрены, то необходимо запустить алгоритм от одной из не рассмотренных вершин.
• Поиск в ширину (breadth-first search, BFS) — метод обхода дерева и поиска пути. Поиск в ширину является одним из неинформированных алгоритмов поиска. Поиск в ширину работает путём последовательного просмотра отдельных уровней дерева, начиная с узла-источника. Рассмотрим все рёбра, выходящие из узла. Если очередной узел является целевым узлом, то поиск завершается; в противном случае узел добавляется в очередь. После того, как будут проверены все рёбра, выходящие из узла, из очереди извлекается следующий узел, и процесс повторяется.
Давайте подробно рассмотрим каждый из алгоритмов обхода.
Поиск в глубину (DFS)
DFS исследует все возможные пути вплоть до некоторого листа дерева, возвращается и исследует другой путь (осуществляя, таким образом, поиск с возвратом). Давайте посмотрим на пример с этим типом обхода.
Результатом этого алгоритма будет: 1–2–3–4–5–6–7.
Давайте разъясним это подробно.
Проход в глубь дерева, а затем возврат к исходной точке называется алгоритмом DFS.
После знакомства с этим алгоритмом обхода, рассмотрим различные типы DFS-алгоритма: предварительный обход (pre-order), симметричный обход (in-order) и обход в обратном порядке (post-order).
Предварительный обход
Именно это мы и делали в вышеприведенном примере.
1. Записать значение узла.
2. Перейти к левому потомку и записать его. Это выполняется тогда и только тогда, когда имеется левый потомок.
3. Перейти к правому потомку и записать его. Это выполняется тогда и только тогда, когда имеется правый потомок.
Сравнение* древовидных графов
* На самом деле не совсем так. При разработке информационной системы, частью которой является различная обработка конструкторско-технологической документации, у меня возникла проблема, которую вкратце можно описать следующим образом. Сегодня мы имеем один состав изделия, за день приходит несколько изменений по различным частям этого изделия и к вечеру уже неясно, что же изменилось? Изделия порой могут иметь более 10 000 элементов в составе, элементы не уникальны, а реальность такова, что изменения по составу могут активно приходить, хотя изделие уже почти готово. Непонимание объема изменений усложняет планирование.
Состав изделия можно представить в виде древовидного графа. Не найдя подходящего способа сравнения двух графов, я решил написать свой велосипед.
Задача
В течение дня различные изменения из конструкторской системы приходят в систему учета. На данных из системы учета строится планирование производства. Условия позволяют принять все изменения за день и пересчитать спецификацию изделия ночью. Но, как я писал выше, непонятно, чем отличается вчерашнее состояние от состояния сегодняшнего.
Хочется видеть что ушло из дерева изделия, а что добавилось. Так же хочется видеть какая деталь или сборка заменила другую деталь или сборку. Например, если в ветке дерева добавился промежуточный узел, то в таком случае неправильно будет считать, что все нижестоящие элементы удалились со старых мест и вставились на новые места. Они остались на своих местах, но произошла вставка промежуточного узла. Кроме того, элемент может «путешествовать» вверх и вниз только внутри одной ветки дерева, это обусловлено спецификой техпроцесса изготовления.
Подготовка
Спецификация изделия пересчитывается PL/SQL-процедурой внутри Oracle. Поэтому я счел логичным сделать и свой поиск изменений на PL/SQL.

Так же проставим на элементах суммарного дерева их уровень вложенности, чтобы в дальнейшем не вычислять его каждый раз.
Сохраним состояние таблицы mr_order_tree_comp для пересчитываемого заказа, это понадобится в будущем. Я использовал коллекцию, но думаю, что можно применить и временную таблицу.
«Сложение» деревьев
Теперь нужно пройти получившееся дерево по уровням и по узлам в поисках изменений. Для начала определим максимальный уровень:
Когда элемент обработан, помещать его в некоторый список обработанных элементов. Я использовал следующую процедуру:
«Обработанность» элемента возвращала функция
которая просматривала ту же коллекцию.
Цикл выглядит следующим образом:
Для (rl.stat = 1) логика аналогична.
Поиск «похожих» элементов
Но что делать, когда произошла замена одного узла на другой, был вставлен узел в середину или узел из середины был удален?
Для определения описанных ситуаций я не нашел ничего умнее как просто сравнить составы двух узлов с целью определения отношения количества одинаковых kts_item_id к общему количеству элементов. Если значение данного отношения больше определенного значения, то узлы взаимозаменяемы. Если на текущей итерации цикла у узла есть несколько вариантов замены, то берется вариант с наибольшим «коэффициентом похожести».
Возможно, таким смелым решением я когда-нибудь выстрелю себе в ногу.
Удалось найти один элемент в этом узле
Перецепим на него содержимое текущего узла без раздумий. При условии, что оба элемента являются сборками. Текущий элемент не удаляется. Почему? Если в узлах вообще нет одинаковых элементов, то в дальнейшем всё будет возвращено на свои места.
В итоге часть элементов будет перецеплена, и дерево будет иметь следующий вид. 
Если дополнительный корневой элемент, который был добавлен в начале, не нужен, то его можно удалить.
Теперь можно взять все оставшиеся элементы со статусом 0 и 1, и начиная с них пройти вверх к корню. Если будет найден такой же элемент с «противоположным статусом», то сравнить их, удалить из дерева элемент с 0, а у элемента с 1 сменить статус.
После этого дерево получает искомый вид.
Полагаю, что есть более красивые, быстрые и правильные способы сравнения деревьев. Это мой вариант и надеюсь, что он будет полезен кому-то и покажет, как можно делать или как не надо делать.
Иерархические структуры данных и Doctrine
Введение
Хранение иерархических данных (или попросту — деревьев) в реляционных структурах задача довольно нетривиальная и вызывает некоторые проблемы, когда разработчики сталкиваются с подобной задачей.
В первую очередь, это связано с тем, что реляционные базы не приспособлены к хранению иерархических структур (как, например, XML-файлы), структура реляционных таблиц представляет из себя простые списки. Иерархические же данные имеют связь «родитель-наследники», которая не реализована в реляционной структуре.
Тем не менее, задача «хранить деревья в базе данных» рано или поздно возникает перед любым разработчиком.
Ниже мы подробно рассмотрим, какие существуют подходы в организации хранения деревьев в реляционных БД, а также рассмотрим инструментарий, который нам предоставляет ORM Doctrine для работы с такими структурами.
Список смежных вершин (Adjacency List)
Описание структуры
Как правило, такая структура данных предполагает хранение информации о смежных вершинах нашего дерева. Давайте рассмотрим простейший граф с темя вершинами (1,2,3):
Рис. 1. Граф с тремя вершинами
Как видим каждый элемент данного графа хранит информацию о связи с другими элементами, т.е.:
Фактически, для построения дерева такой граф избыточен, т.к. для привычной ветвистой структуры нам нужно хранить только связь «родитель-наследник», т.е.:
Тогда мы получим дерево с одним корневым элементом (1) и двумя ветками (2,3):
В принципе, тот и другой графы можно, при желании, отобразить в базе данных с помощью списка смежных вершин, но, поскольку нас интересуют именно деревья, остановимся на них.
Итак, чтобы хранить в базе данных иерархическую структуру методом списка смежных вершин (Adjacency List), нам необходимо хранить информацию о связях «наследник-родитель» в таблицах с данными. Давайте рассмотрим реальный пример дерева:
Рис. 3. Древовидная структура методом смежных вершин
На рисунке квадратами обозначены узлы деревьев. У каждого узла есть имя (верхний прямоугольник внутри квадрата), идентификатор (левый нижний квадрат) и ссылка на идентификатор родителя (правый нижний квадрат). Как видно из Рис. 3, каждый наследник в такой структуре ссылается на своего предка. В терминах БД мы можем это отобразить следующим образом в виде таблицы:
Рис. 4. Таблица данных дерева, построенная методом списка смежных вершин
Следует сразу отметить, что такой алгоритм хранения деревьев обладает определенными как достоинствами, так и недостатками. В первую очередь, он не совсем удобен для чтения — и это его основной недостаток.
Проблемы с чтением из БД менее заметны, если вычитывать все дерево целиком. Это достаточно простой запрос:
Однако в дальнейшем такая выборка подразумевает достаточно емкую программную пост-обработку данных. Сначала нужно рекурсивно перестроить данные с учетом связей «предок-наследник» и лишь потом их можно будет использовать для вывода куда-либо.
Другой вариант чтения дерева целиком:
Результат в данном случае будет такой:
Хотя данные в таком виде уже более приспособлены сразу для вывода, но, как видите, главный недостаток такого подхода — необходимо достоверно знать количество уровней вложенности в вашей иерархии, кроме того, чем больше иерархия, тем больше JOIN’ов — тем ниже производительность.
Тем не менее, данный способ обладает и существенными достоинствами — в дерево легко вносить изменения, менять местами и удалять узлы.
Вывод — данный алгоритм хорошо применим, если вы оперируете с небольшими древовидными структурами, которые часто поддаются изменениям.
С другой стороны, этот алгоритм также довольно уверенно себя чувствует и с большими деревьями, если считывать их порциями вида «знаю родителя — прочитать всех наследников». Хороший пример такого случая — динамически подгружаемые деревья. В этом случае алгоритм практически оптимизирован для такого поведения.
Однако он плохо применим, когда нужно вычитывать какие-либо иные куски дерева, находить пути, предыдущие и следующие узлы при обходе и вычитывать ветки дерева целиком (на всю глубину).
Использование списка смежных вершин в Doctrine
Сначала хотелось бы высказать несколько вводных слов по организации шаблонов таблиц в Doctrine, с помощью которых подобные вещи в ней и реализуются. Те, кто уже знаком с этой концепцией в доктрине, может перескочить несколько абзацев вперед к более интересным вещам.
Итак, сущности, которыми мы оперируем в ORM Doctrine — это активные записи (Active Record). Т.е. объекты, которые совмещают в себе бизнес-логику и сами умеют взаимодействовать с базой данных. Но разработчики Doctrine предусмотрели расширение функциональности объектов записей не только наследованием, но и применением к этим объектам «шаблонов поведения». Это реализуется пакетом Doctrine/Template.
Т.о., если возникает необходимость воспитать активную запись до какого-либо поведения (например, Versionable — проводит аудит всех изменений, I18N — многоязычная или NestedSet — древовидная вида «вложенное множество»), то это можно сделать как раз с помощью данных шаблонов поведения.
Чтобы подключить какой-либо из существующих шаблонов, достаточно сконфигурировать должным образом нашу модель (посредством YAML или прямо в коде базовой таблицы модели).
Когда придет время, мы покажем на примерах, как это сделать.
Пока, к сожалению, или к счастью, но в виде шаблона к таблицам метод списка смежных вершин в Doctrine не реализован. При желании вы можете написать реализацию сами и даже предложить ее разработчикам Doctrine, — это уже на ваше усмотрение.
Тем не менее, основные функции, которые могут быть реализованы в рамках данной модели, можно реализовать в Doctrine и без использования шаблонов поведения. К сожалению, функций работы с деревом мы не получим, но основные задачи решать сможем.
Для этого следует сконфигурировать нашу модель должным образом. Используя YAML опишем структуру нашей таблицы:
А вот теперь самое важное — правильно описать связи в таблице. Там же со следующей строчки напишем:
Теперь соберем нашу модель, запустив команду:
Все. Модель готова. Фактически тоже самое можно было сделать в уже готовом базовом классе BaseAlTree:
Теперь пришло время насладиться результатами нашей работы. Напишем несложный код, отображающий дерево, построенное с отступами на обычной HTML-странице, используя рекурсию.
Обратите внимание, после того, как мы сконфигурировали должным образом связи у нашего объекта модели, нам стали доступны свойства Children и Parent. Однако любое первое обращение к ним на чтение порождает запрос к базе данных. Поэтому, для построения больших деревьев целиком за один проход, такой подход может оказаться довольно затратным.
Но в тоже время, реализовать динамически подгружаемое дерево таким способом — одно удовольствие!
Вложенное множество (Nested Set)
Описание структуры
Об этом алгоритме и его быстродействии, наверное, слышали все веб-разработчики. Да, этот алгоритм действительно очень хорош, когда требуется часто и много обращаться к иерархическим данным на чтение. Рассмотрим суть данного подхода.
При построении дерева на основе вложенных множеств, мы воспользуемся принципом обхода этого дерева слева-направо, как показано стрелками на Рис. 5. Для этого определим для каждого узла дерева целочисленные ключи слева (lft) и справа (rgt) (нижние квадратики внутри узла). И раздадим им во время обхода целочисленные инкрементные значения. Посмотрите что получилось.
Рис. 5. Вложенное множество (Nested Set).
Корневой элемент получил ключи 1 и 14, которые включают в себя диапазон чисел всех остальных ключей. Ветка VEGETABLE получила ключи 2 и 7, которые, в свою очередь, включают весь диапазон чисел ключей всех ее наследников и т.д. Вот они — вложенные множества. Все просто, не так ли?
Давайте воссоздадим такую же структуру в контексте таблицы БД.
Рис. 6. Таблица иерархических данных на основе метода вложенных множеств
Как видите, мы ввели дополнительно еще одно поле в таблицу — level. В нем будет храниться информация об уровне вложенности каждой ветки дерева. В принципе, это делать вовсе не обязательно — уровень вложенности может быть достаточно просто вычислен, но так как данный алгоритм оптимизирован как раз для чтения, то почему бы не выиграть в производительности за счет кеширования информации об уровне? Риторический вопрос…
Чтение дерева из БД
Результат будет таким:
Теоретически, тот же результат мы бы могли получить, вычисляя уровень вложенности на лету:
Попробуйте сравнить результат самостоятельно — он будет идентичен первому. Только сам запрос в данном случае более ресурсоемкий. А так как Nested Set — это оптимальный алгоритм чтения, то небольшая оптимизация в виде кеширования уровня вложенности рядом с остальными данными не такая уж и плохая стратегия.
Таким же, довольно несложным образом мы можем считывать целые ветки, пути из нашего дерева, обходить его узлы и т.д.
Например, если мы хотим извлечь все овощи (VEGETABLE) из нашего примера, это сделать достаточно просто:
Да, быстрое и гибкое чтение, включая агрегацию с внешними связанными данными — конек данного алгоритма.
Тем не менее, не бывает худа без добра, и в данном случае, значительные трудности начинаются когда нам необходимо внести изменения в Nested Set дерево или удалить какую-либо из его ветвей.
Это связано, в первую очередь, с тем, что при изменениях, нам будет необходимо пересчитать все ключи той части дерева, которая находится справа от изменяемого узла, а также обновить информацию об уровнях вложенности. И все это не сделать одним простым запросом.
Добавление новой ветки
Предположим, что мы хотим добавить новую ветку с именем SEA FOOD в наше дерево на одном уровне с VEGETABLES и FRUIT.
Если вы используете в MySQL таблицы MYISAM, или версию, которая не поддерживает транзакции, вы можете вместо BEGIN и COMMIT использовать блокировки на запись:
Как видите, задача на добавление новой ветки достаточно затратная и нетривиальная. Тем не менее, решаемая.
Удаление ветки
Давайте теперь попробуем удалить вновь созданную ветку:
Вывод — Nested Set действительно хорош, когда нам необходимо считывать структуру деревьев из БД. При этом он одинаково хорош для деревьев любого объема.
Тем не менее, для иерархических структур, которые подвергаются частому изменению он, очевидно, не будет являться оптимальным выбором.
Использование Nested Set в Doctrine
А вот этот метод имеет отражение в Doctrine в виде реализации шаблона поведения, который мы можем привязать к нашей модели.
Сделать это довольно просто, методом конфигурации модели через YAML-конфиг или прамо в коде базового класса.
Как видите, достаточно просто указать actAs: [NestedSet] в описании класса.
Однако Doctrine предоставляет более гибкую конфигурацию NestedSet модели. Например, вы можете хранить в одной таблице несколько деревьев. Для этого, вам необходимо ввести в таблицу дополнительное поле, в котором вы будете хранить идентификатор корня дерева для каждой записи.
В этом случае конфигурацию следовало бы записать так:
Все то же самое могло бы быть проделано в существующем базовом классе модели.
Для первого случая:
Для второго случая (несколько деревьев):
Заметьте, Doctrine использует ‘root_id’ в качестве имени поля по умолчанию. Поэтому вам не обязательно указывать эту опцию, если оно совпадает с именем в вашей реальной таблице. В противном случае вы можете его задать.
Примеры работы с деревьями Nested Set в Doctrine
Извлекаем и печатаем все дерево на экран:
Посмотрите как это просто!
За дополнительными примерами и информацией вы можете обратиться к официальной документации Doctrine, разделы 8.2.4 и 8.2.5
Материализованный путь (Materialized Path)
Описание структуры
Еще один довольно интересный подход для хранения иерархических структур. Основная идея алгоритма в хранении полного пути к узлу от вершины дерева. Выглядит это примерно так:
Рис. 7. Древовидная структура, организованная по принципу «материализованый путь»
Принцип формирования таких путей достаточно прост. Глубина пути — это уровень дерева. Внутри ветки нумерация — инкрементная. Другими словами, VEGETABLE — первый ребенок FOOD, FRUIT — второй ребенок и т.д.
Проще будет взглянуть на это в виде таблицы:
Возможно, так даже более наглядно.
В базе данных все это находит следующее отражение.
Рис. 8. структура таблицы иерархических данных, организованных по принципу «материализованный путь»
В чем же преимущество такого подхода?
Во-первых, по сравнению с Nested Set, он более поддается изменениям. В то же время остается достаточно удобным для выборки деревьев целиком и их частей. Но, и он не идеален. Особенно по части поиска предков ветки.
Поиск пути к узлу:
Вычисление уровня вложенности.
Для решения этой задачи нам в принципе достаточно посчитать кол-во точек (или других разделителей, если вы используете не точку) в путях. К сожалению, MySQL не имеет подходящей функции, но мы можем ее реализовать достаточно просто своими силами:
Выбор ветки:
Обратите внимание, в данном примере мы воспользовались нашей самописной функцией и это было достаточно удобно.
Поиск родителя:
Как видите, все эти запросы не тешат максимальной производительностью (по сравнению с предыдущим методом), но, тем не менее, использование именно этого алгоритма может быть заметно удобнее, для деревьев, над которыми часто выполняются как операции чтения, так и изменения.
Насколько известно автору, алгоритм довольно уверенно себя чувствует на достаточно больших объемах данных.
Следует отметить, что наиболее неприятной в данном алгоритме будет операция вставки узла в середину уже существующей структуры (между другими узлами), т.к. это повлечет изменение всех путей в нижележащих узлах. Хотя, справедливости ради, следует сказать, что такая операция окажется нетривиальной для любой модели хранения данных. Другая тяжелая операция — это перенос одной ветки в другую.
А вот удаление, добавление в конец или изменение узла — это операции довольно простые, и, как правило, не вызывают сложностей в данной модели.
Как видно из примеров, данный алгоритм также можно несколько оптимизировать на чтение, путем введения ещё одного поля level, как это было сделано для списков смежных вершин (Nested Set). Однако это несколько усложнит операции добавления, изменения и удаления узлов дерева, т.к. уровни придется пересчитывать для всего или части дерева при каждом изменении. В конечном счете, именно разработчику решать, в какую сторону следует делать перекос производительности.
Использование в Doctrine
К сожалению, на данный момент, этот метод хранения деревьев пока не нашел своей реализации в ORM Doctrine (текущая версия на момент написания материала — 1.0.4, 1.1.0 — в альфа версии также реализации не имеет).
Тем не менее есть все предпосылки полагать, что его реализация появится в будущем, т.к. исходные коды библиотеки содержат в пакете Doctrine/Tree абстракный пустой класс с именем MaterializedPath.
Автор будет следить за событиями и обновит эту статью, как только реализация найдет свое отражение, так что можете сюда вернуться позже.
Комбинированный подход
Фактически, комбинирование подходов на уровне БД ограничивается вводом поля, хранящего ссылку на родительскую запись в таблицы списков смежности и материализованных путей:
Рис. 9. Таблицы моделей иерархических структур данных AL+MP и AL+NS
Последствия такого подхода очевидны.
AL+MP
AL+NS
Для связки AL+NS взаимовыгодность не столь очевидна. В первую очередь это объясняется тем, что недостатки от проблем изменения узлов дерева в модели NS напрочь убивают в этой сфере все достоинства AL. Это значит, что такую связку следует рассматривать лишь как качественное улучшение поиска родителей и наследников заданного узла в алгоритме NS, а также как повышение надежности самого алгоритма (ключи можно всегда перестроить в случае порчи — информацию о связях хранит AL). Утверждение о повышении надежности справедливо и для предыдущей комбинации методов. Но ведь и это качественное улучшение, хотя и не такое очевидное, не так ли?
Заключение
В данной статье мы рассмотрели несколько основных методов хранения иерархических данных в реляционных БД и очертили все их достоинства и недостатки. Также мы показали на практике, какие из них доступны для использования в реализации ORM Doctrine, и как их использовать.
Очевидно, что даже выбор того или иного метода в каждом конкретном случае — задача не такая уж и простая, но автор надеется, что данный материал будет способствовать принятию осознанного и правильного решения, а также будет способствовать творческому процессу поиска новых и более оптимальных решений.