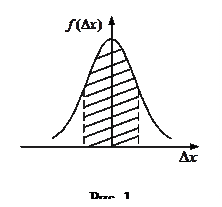
Что такое доверительный интервал и надежность

Точность оценки, доверительная вероятность (надежность). Доверительный интервал

Точечной называют оценку, которая определяется одним числом. Все оценки, рассмотренные выше,- точечные. При выборке малого объема точечная оценка может значительно отличаться от оцениваемого параметра, т. е. приводить к грубым ошибкам. По этой причине при небольшом объеме выборки следует пользоваться интервальными оценками.

Однако важно подчеркнуть, что для малых выборок (n 2 с k степенями свободы, то величина

(*)

распределена по закону Стьюдента с k степенями свободы. Пусть количественный признак X генеральной совокупности распределен нормально, причем М(Х)=а, σ(Х)= σ. Если из этой совокупности извлекать выборки объема n и по ним находить выборочные средние, то можно доказать, что выборочная средняя распределена нормально, причем (см. гл. VIII, § 9)

, .

Тогда случайная величина

(**)

также имеет нормальное распределение как линейная функция нормального аргумента 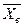(см. гл. XII, § 10, замечание), причем М (Z) = 0, σ(Z)=l. Доказано, что случайные величины Z и

(***)

Следовательно, подставив (**) и (***) в (*), получим величину

,

которая распределена по закону Стьюдента с k = n-1 степенями свободы.

Источник

Что такое доверительный интервал и надежность

I 331. Игральная кость подбрасывается 300 раз. Какова вероятность того, что относительная частота появления шести очков на верхней грани кости отклонится от вероятности появления события в одном испытании по абсолютной величине не более чем на 0,05?

332. Сколько раз надо подбросить монету, чтобы с вероятностью 0,95 можно было ожидать, что относительная частота появления «герба» отклонится от вероятности этого события по абсолютной величине не более чем на 0,1?

334. Исследовалось время безотказной работы 50 лазерных принтеров. Из априорных наблюдений известно, что среднее квадратическое отклонение времени безотказной работы ч. По результатам исследований получено среднее время безотказной работы ч. Постройте 90%-й доверительный интервал для среднего времени безотказной работы.

336. Произведено 16 измерений одним прибором некоторой физической величины, причем исправленное среднее квадратическое отклонение случайных ошибок измерений оказалось равным 0,7. Найдите интервал ошибок прибора с надежностью 0,99. Предполагается, что ошибки измерений распределены нормально.

II 337. Время (в минутах) обслуживания клиентов в железнодорожной кассе представлено выборкой: 2,0; 1,5; 1,0; 1,0; 1,25; 3,5; 3,0; 3,0; 3.75; 3,7; 4,0; 6,0; 7,0; 1,5; 8,0; 3,5; 5,0; 3,5; 14,0; 12,0; 15,1; 18,0; 18,5; 17,0. Определите процент клиентов, время обслуживания которых более 12 минут и менее 5 минут.

338. Из генеральной совокупности извлечена выборка объема :

Оцените с надежностью 0,9 математическое ожидание нормально распределенного признака генеральной совокупности с помощью доверительного интервала.

III 339. Результаты исследования длительности оборота оборотных средств торговых фирм города (в днях) представлены в группированном виде:

Постройте доверительный интервал с надежностью 0,95 для средней длительности оборотных средств торговых фирм города при условии, что среднее квадратическое отклонение неизвестно (известно и равно 10 дням).

340. Найти методом наибольшего правдоподобия оценку параметра распределения Пуассона

Источник

Доверительный интервал и доверительная вероятность

Для подавляющего большинства простых измерений достаточно хорошо выполняется так называемый нормальный закон случайных погрешностей (закон Гаусса), выведенный из следующих эмпирических положений.

1) погрешности измерений могут принимать непрерывный ряд значений;

2) при большом числе измерений погрешности одинаковой величины, но разного знака встречаются одинаково часто,

3) чем больше величина случайной погрешности, тем меньше вероятность ее появления.

, (2)

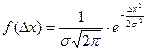
где 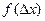— функция распределения случайных ошибок (погрешностей), характеризующая вероятность появления ошибки , σ – средняя квадратичная ошибка.

Величина σ не является случайной величиной и характеризует процесс измерений. Если условия измерений не изменяются, то σ остается постоянной величиной. Квадрат этой величины называют дисперсией измерений. Чем меньше дисперсия, тем меньше разброс отдельных значений и тем выше точность измерений.

Точное значение средней квадратичной ошибки σ, как и истинное значение измеряемой величины, неизвестно. Существует так называемая статистическая оценка этого параметра, в соответствии с которой средняя квадратичная ошибка равняется средней квадратичной ошибке среднего арифметического . Величина которой определяется по формуле

, (3)

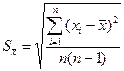
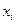
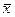
где — результат i-го измерения; — среднее арифметическое полученных значений; n – число измерений.

Чем больше число измерений, тем меньше и тем больше оно приближается к σ. Если истинное значение измеряемой величины μ, ее среднее арифметическое значение, полученное в результате измерений , а случайная абсолютная погрешность , то результат измерений запишется в виде .

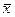
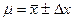
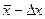
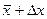
Интервал значений от до , в который попадает истинное значение измеряемой величины μ, называется доверительным интервалом. Поскольку является случайной величиной, то истинное значение попадает в доверительный интервал с вероятностью α, которая называется доверительной вероятностью, или надежностью измерений. Эта величина численно равна площади заштрихованной криволинейной трапеции. (см. рис.)

Все это справедливо для достаточно большого числа измерений, когда близка к σ. Для отыскания доверительного интервала и доверительной вероятности при небольшом числе измерений, с которым мы имеем дело в ходе выполнения лабораторных работ, используется распределение вероятностей Стьюдента. Это распределение вероятностей случайной величины , называемой коэффициентом Стьюдента, дает значение доверительного интервала в долях средней квадратичной ошибки среднего арифметического .

. (4)

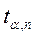
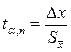
Функция распределения табулирована (табл.1). Значение коэффициента Стьюдента находится на пересечении строки, соответствующей числу измерений n, и столбца, соответствующего доверительной вероятности α

Таблица 1.

Пользуясь данными таблицы, можно:

1) определить доверительный интервал, задаваясь определенной вероятностью;

2) выбрать доверительный интервал и определить доверительную вероятность.

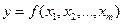
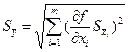
При косвенных измерениях среднюю квадратичную ошибку среднего арифметического значения функции вычисляют по формуле

. (5)

Доверительный интервал и доверительная вероятность определяются так же, как и в случае прямых измерений.

Источник

Доверительные интервалы для параметров нормального распределения

1. Надежность. Доверительные интервалы. Пусть — оцениваемый параметр,

— его оценка, составленная из . Если известно, что оценка является несмещенной и состоятельной, то по данным выборки вычисляют значение и считают его приближением истинного значения . При этом среднее квадратичное отклонение (если его вообще вычисляют) оценивает порядок ошибки. Такие оценки называются точечными.

Например, в предыдущем параграфе речь шла о точечных оценках генеральной средней и генеральной дисперсии. В общем случае, когда о распределении признака X ничего неизвестно, это уже немало. Если же о распределении имеется какая-либо информация, то можно сделать больше.

Здесь речь будет идти об оценке параметров а к о случайной величины,

имеющей нормальное распределение. Это очень важный случай. Например (см. § 2.7), результат измерения имеет нормальное распределение. В этом случае становится возможным применять так называемое интервальное оценивание, к изложению которого мы и переходим.

Пусть >0 некоторое число если неравенство выполняется 0 называется вероятность у того, что интервал ( — , + ) покроет параметр т.е.

где коэффициент В_n зависит от объема выборки.

* Стьюдент — псевдоним английского статистика И. О. Госсета.

Потребуем, чтобы выполнялось соотношение

Р(|Т| 30 распределение Стьюдента практически не отличается от нормированного нормального распределения(см. § 2.7, п. 2).

4. Доверительный интервал для среднего квадратичного отклонения. Для нахождения доверительного интервала для среднего квадратичного отклонения а будем использовать следующее предложение, устанавливаемое аналогично двум предыдущим

С надежностью γ можно утверждать, что доверительный интервал (s-sq; s+sq) покрывает неизвестный параметр σ; точность оценки δ = sq.

В приложении 5 приведена таблица значений q=q(γ, n) для различных значений n и обычно задаваемых значений надежности γ.

Пример 1. Признак X распределен в генеральной совокупности нормально. Найдем доверительный интервал для ог с надежностью γ =0,95, если n = 20; s=0,40. Для надежности

γ =0,95 и n = 20 находим в таблице приложения 5 q = 0,37. Далее, sq = 0,40*0,37 = 0,15.

Границы доверительного интервала 0,40-0,15= 0,25 и 0,40 + 0,15 = 0,55. Итак, доверительный интервал (0,25; 0,55) покрывает σ_r с надежностью 0,95.

Пример 2. На ферме испытывалось влияние витаминов на прибавку в массе телят. С этой целью было осмотрено 20 телят одного возраста. Средняя масса их оказалась равной 340 кг, а «исправленное» среднее квадратичное отклонение — 20 кг.

1) доверительный интервал для математического ожидания а с

надежностью 0,95; 2) доверительный интервал для среднего квадратичного отклонения с той же надежностью.

При решении задачи будем исходить из предположения, что данные пробы взяты из нормальной генеральной совокупности.

Можно считать, что в данном случае истинная масса измерена достаточно точно (отклонение порядка 9,4/340= 0,03).

подтверждается опытом). Таким образом, все предположения, которые были сделаны при выводе доверительных интервалов в пп. 2 и 3 настоящего параграфа, выполняются,

следовательно, мы вправе использовать полученные в них предложения. Так как обычно а неизвестно, следует пользоваться предложением, найденным в п. 3 данного параграфа.

Пример. По данным девяти независимых равноточных измерений физической величины найдены среднее арифметическое результатов отдельных измерений х_B = 42,319 и «исправленное» среднее квадратичное отклонение s = 5,0.

Требуется оценить истинное значение а измеряемой величины с надежностью γ =0,99.

Истинное значение измеряемой величины равно ее математическому ожиданию. Поэтому задача сводится к оценке математического ожидания (при неизвестном σ) при помощи доверительного интервала

покрывающего а с заданной надежностью γ =0,99.

Пользуясь таблицей приложения 4 по γ =0,99 и n = 9, находим t_γ=3,36.

Найдем точность оценки:

δ = t_γs/√n = 3,36*5/√9 = 3,36*5/3 = 5,60.

Границы доверительного интервала

и 42,319 + 5,60 = 47,919.

Итак, с надежностью γ =0,99 истинное значение измеренной величины а заключено в доверительном интервале 36,719 1/3

Найдите вероятность того, что в результате испытания величина X примет значение, заключенное в интервале (0; 1/3)

18. Случайная величина X на всей оси Ох задана интегральной функ­цией F(x)= . Найдите вероятность того, что в результате ис­пытания величина X примет значение, заключенное в интервале (0; 1).

19. Случайная величина X задана интегральной функцией

20. Функция

является плотностью вероятности случайной величины X. Найдите коэф­фициент а и функцию распределения F(x).

[ ]

21. Случайная величина Х задана по всей оси Ох плотностью вероятности

Найдите постоянный параметр а.

22. Случайная величина X задана плотностью вероятности

0 при х

Найдите коэффициент а. [a=1 ]

23. Случайная величина X задана плотностью вероятности f(x) = 2/3sin3x в интервале (0;П/3), вне этого интервала f(х) = 0. Найдите вероятность того, что X примет значение, принадлежащее интервалу (П/6;П/4)

[ ]

24. Случайная величина X задана плотностью вероятности

Найдите математическое ожидание случайной величины X

25. Случайная величина X задана плотностью вероятности

Найдите математическое ожидание и дисперсию случайной величины X.

26. Два равносильных шахматиста играют в шахматы. Что вероятнее выиграть: одну партию из двух или две партии из четырех (ничьи во внимание не принимаются)?

[Вероятнее выиграть одну партию из двух]

27. Пусть всхожесть семян данного растения составляет 70%. Опре­делите вероятность того, что из трех посеянных семян взойдут: а) два; б) не менее двух.- [а) 0,441; б) 0,784]

28. В семье пятеро детей. Найдите вероятность того, что среди этих детей два мальчика. Вероятность рождения мальчика принять равной 0,51.

29. Монету бросали четыре раза. Чему равна при этом вероятность вы­падения герба два раза?

30. Монета подбрасывается три раза. Какова вероятность того, что герб появится не менее двух раз?

31. Монета подбрасывается три раза. Рассматривается случайная вели­чина X— число появлений герба. Найдите закон распределения случайной величины X.

32. Найдите математическое ожидание числа бракованных изделий в партии из 10 000 изделий, если каждое изделие может оказаться брако­ванным с вероятностью 0,005.

33. Из всей выпускаемой фабрикой продукции 98% составляют изде­лия со Знаком качества. Найдите: а) математическое ожидание и б) дис­персию числа изделий со Знаком качества в партии из 5000 изделий.

34. Подлежат исследованию 1200 проб руды. Пусть вероятность про­мышленного содержания металла в каждой пробе равна 0,09. Найдите: а) математическое ожидание и б) дисперсию числа проб с промышленным содержанием металла.

35. Математическое ожидание и среднее квадратическое отклонение нормально распределенной случайной величины X соответственно равны 3 и 2. Найдите плотность вероятности случайной величины X f(x).

36. Напишите дифференциальную функцию нормально распределен­ной случайной величины X, зная, что М(Х) = 3, D(X) = 16.

37. Нормально распределенная случайная величина X задана дифференциальной функцией

Найдите математическое ожидание и дисперсию X.

38. Математическое ожидание и среднее квадратическое отклонение нор­мально распределенной случайной величины X соответственно равны 10 и 2. Найдите вероятность того, что в результате испытания Х примет значе­ние, заключенное в интервале (12; 14).

39. Математическое ожидание и среднее квадратическое отклонение нормально распределенной случайной величины Х соответственно равны 20 и 5. Найдите вероятность того, что в результате испытания X примет значе­ние в интервале (15; 25).

40. Детали, выпускаемые цехом, по размеру диаметра распределяются по нормальному закону с параметрами: математическое ожидание равно 5 см, а среднее квадратическое отклонение равно 0,9 см. Найдите вероятность того, что отклонение диаметра наудачу взятой детали от математи­ческого ожидания по абсолютной величине будет меньше 2 см.

41. Проводится взвешивание некоторого вещества без систематических ошибок. Случайные ошибки взвешивания подчинены нормальному закону со средним квадратическим отклонением = 20 г. Найдите вероятность того, что взвешивание будет проведено с ошибкой, которая по абсолютной ве­личине меньше 10 г.

42. АТС получает в среднем за час 300 вызовов. Какова вероятность того, что за данную минуту она получит точно 2 вызова?

43. Среди 1000 человек приблизительно 8 левшей. Какова вероятность того, что среди сотни наугад выбранных человек не окажется ни одного левши?

44. Монету подбрасывают 100 раз. Какова вероятность того, что при этом герб выпадет ровно 50 раз?

45. Какова вероятность того, что при 200-кратном бросании монеты число случаев выпадения герба удовлетворяет неравенству 95

Источник