Что такое дополнительный граф
Дополнение графа
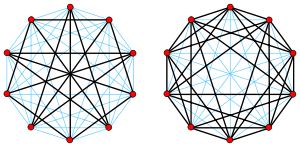
В теории графов дополнением или обратным к графу G называется такой граф H, имеющий то же множество вершин, что и G, но в котором две несовпадающие вершины смежны тогда и только тогда, когда они не смежны в G. Чтобы найти обратный граф, дополните данный граф до полного и удалите все ребра, которые уже были до этого.
Формальное определение
Пуcть G=(V,E) — простой граф и пусть множество K содержит все двухэлементные подмножества множества V. Тогда H=(V,K\E) является дополнением графа G.
Свойства
Дополнением пустого графа (содержащего только вершины, но не ребра) является полный граф, и наоборот.
Смотреть что такое «Дополнение графа» в других словарях:
дополнение графа — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN complement of graph … Справочник технического переводчика
дополнение дерева графа — Все связи графа электрической цепи. [ГОСТ Р 52002 2003] Тематики электротехника, основные понятия Синонимы дополнение дерева графа электрической цепи … Справочник технического переводчика
дополнение — 03.01.03 дополнение (символ) [overhead]: Часть символа штрихового кода, дополняющая знаки символа, кодирующие данные, для придания символу установленной структуры и состоящая из вспомогательных знаков и контрольных знаков символа. Источник … Словарь-справочник терминов нормативно-технической документации
дополнение дерева графа (электрической цепи) — 207 дополнение дерева графа (электрической цепи) Все связи графа электрической цепи Источник: ГОСТ Р 52002 2003: Электротехника. Термины и определения основных понятий оригинал документа … Словарь-справочник терминов нормативно-технической документации
Дополнение дерева графа (электрической цепи) — 1. Все связи графа электрической цепи Употребляется в документе: ГОСТ Р 52002 2003 Электротехника. Термины и определения основных понятий … Телекоммуникационный словарь
Германия (дополнение к статье) — или Германская империя (Deutschland, Deutsches Reich) в настоящее время состоит из 22 конституционных государств, 3 вольных городов и 1 имперской страны. Площадь и население. Г., не считая колоний, занимает 540743 кв. км, с 56367178 жителями (по… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Венгрия (дополнение к статье) — (см.) конституционное королевство, одна из составных частей Австро Венгерской монархии. Площадь 324851 кв. км; в 1902 г. жителей было 19692807. В. состоит из собственно В. и королевства Хорватии и Славонии. Собственно В. делится на 7 частей… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Япония (дополнение к статье) — (ñì.) конституционная империя в Азии. По данным 1905 г. Я. (не считая отошедших к ней по Портсмутскому договору 5 сент. 1905 г. Квантуна и южн. части о ва Сахалина) занимает 417412 кв. км; жителей 50853590. Свыше 100 тыс. жителей… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Маккавейский, Никола Корнильевич (дополнение к статье) — (род. в 1864 г.) писатель, воспитанник киевской духовной академии, в которой состоит профессором пастырского богословия и педагогики. Главнейшие труды М. после 1891 г.: «Религия и народность, как основы воспитания» (Киев, 1895); «К … Большая биографическая энциклопедия
Граф (математика)
В математической теории графов и информатике граф — это совокупность непустого множества вершин и множества пар вершин (связей между вершинами).
Объекты представляются как вершины, или узлы графа, а связи — как дуги, или рёбра. Для разных областей применения виды графов могут различаться направленностью, ограничениями на количество связей и дополнительными данными о вершинах или рёбрах.
Многие структуры, представляющие практический интерес в математике и информатике, могут быть представлены графами. Например, строение Википедии можно смоделировать при помощи ориентированного графа (орграф), в котором вершины — это статьи, а дуги (ориентированные рёбра) — гиперссылки (см. Тематическая карта).
Содержание
Определения
Теория графов не обладает устоявшейся терминологией. В различных статьях под одними и теми же терминами понимаются разные вещи. Ниже приведены наиболее часто встречаемые определения.
Граф, или неориентированный граф 
— это упорядоченная пара 
, для которой выполнены следующие условия:
(а значит и, 
, иначе оно было бы мультимножеством) обычно считаются конечными множествами. Многие хорошие результаты, полученные для конечных графов, неверны (или каким-либо образом отличаются) для бесконечных графов. Это происходит потому, что ряд соображений становится ложным в случае бесконечных множеств.
Вершины и рёбра графа называются также элементами графа, число вершин в графе 
— порядком, число рёбер 
— размером графа.
Вершины 
и 
называются концевыми вершинами (или просто концами) ребра 
. Ребро, в свою очередь, соединяет эти вершины. Две концевые вершины одного и того же ребра называются соседними.
Два ребра называются смежными, если они имеют общую концевую вершину.
Два ребра называются кратными, если множества их концевых вершин совпадают.
Ребро называется петлёй, если его концы совпадают, то есть 
.
Степенью 
вершины называют количество инцидентных ей рёбер (при этом петли считают дважды).
Вершина называется изолированной, если она не является концом ни для одного ребра; висячей (или листом), если она является концом ровно одного ребра.
Ориентированный граф
Ориентированный граф (сокращённо орграф) — это упорядоченная пара 
, для которой выполнены следующие условия:
Дуга — это упорядоченная пара вершин 
, где вершину называют началом, а 
— концом дуги. Можно сказать, что дуга 
ведёт от вершины к вершине .
Смешанный граф
Смешанный граф — это граф, в котором некоторые рёбра могут быть ориентированными, а некоторые — неориентированными. Записывается упорядоченной тройкой 
, где , и 
определены так же, как выше.
Ориентированный и неориентированный графы являются частными случаями смешанного.
Изоморфные графы
Граф называется изоморфным графу 
, если существует биекция 
из множества вершин графа в множество вершин графа , обладающая следующим свойством: если в графе есть ребро из вершины в вершину 
, то в графе должно быть ребро из вершины 
в вершину 
и наоборот — если в графе есть ребро из вершины в вершину , то в графе должно быть ребро из вершины 
в вершину 
. В случае ориентированного графа эта биекция также должна сохранять ориентацию ребра. В случае взвешенного графа биекция также должна сохранять вес ребра.
Прочие связанные определения
Путём (или цепью) в графе называют конечную последовательность вершин, в которой каждая вершина (кроме последней) соединена со следующей в последовательности вершин ребром.
Ориентированным путём в орграфе называют конечную последовательность вершин 
, для которой все пары 
являются (ориентированными) рёбрами.
Циклом называют путь, в котором первая и последняя вершины совпадают. При этом длиной пути (или цикла) называют число составляющих его рёбер. Заметим, что если вершины и являются концами некоторого ребра, то согласно данному определению, последовательность 
является циклом. Чтобы избежать таких «вырожденных» случаев, вводят следующие понятия.
Путь (или цикл) называют простым, если ребра в нём не повторяются; элементарным, если он простой и вершины в нём не повторяются. Несложно видеть, что:
Бинарное отношение на множестве вершин графа, заданное как «существует путь из в », является отношением эквивалентности и, следовательно, разбивает это множество на классы эквивалентности, называемые компонентами связности графа. Если у графа ровно одна компонента связности, то граф связный. На компоненте связности можно ввести понятие расстояния между вершинами как минимальную длину пути, соединяющего эти вершины.
Всякий максимальный связный подграф графа G называется связной компонентой (или просто компонентой) графа . Слово «максимальный» означает максимальный относительно включения, то есть не содержащийся в связном подграфе с большим числом элементов
Ребро графа называется мостом, если его удаление увеличивает число компонент.
Дополнительные характеристики графов
Обобщение понятия графа
Простой граф является одномерным симплициальным комплексом.
Более абстрактно, граф можно задать как тройку 
, где и — некоторые множества (вершин и рёбер, соотв.), а 
— функция инцидентности (или инцидентор), сопоставляющая каждому ребру 
(упорядоченную или неупорядоченную) пару вершин и из (его концов). Частными случаями этого понятия являются:
Под данное выше определение не подходят некоторые другие обобщения:
Способы представления графа в информатике
Матрица смежности
Таблица, где как столбцы, так и строки соответствуют вершинам графа. В каждой ячейке этой матрицы записывается число, определяющее наличие связи от вершины-строки к вершине-столбцу (либо наоборот).
Недостатком являются требования к памяти, прямо пропорциональные квадрату количества вершин.
Матрица инцидентности
Каждая строка соответствует определённой вершине графа, а столбцы соответствуют связям графа. В ячейку на пересечении 
-ой строки с 
-м столбцом матрицы записывается:
1 в случае, если связь «выходит» из вершины , −1, если связь «входит» в вершину, 0 во всех остальных случаях (то есть если связь является петлёй или связь не инцидентна вершине)
Данный способ является самым ёмким (размер пропорционален 
) для хранения, но облегчает нахождение циклов в графе.
Список рёбер
Список рёбер — это тип представления графа, подразумевающий, что каждое ребро представляется двумя числами — номерами вершин этого ребра.
Языки описания и программы построения графов
Для описания графов в целях, пригодных для машинной обработки и одновременно удобном для человеческого восприятия используется несколько стандартизированных языков, среди которых:
Отметим специализированные коммерческие программы для построения графов:
Из бесплатных можно отметить:
Для визуализации графов можно использовать:
См. также
Литература
Полезное
Смотреть что такое «Граф (математика)» в других словарях:
Граф — Граф: От древневерхненемецкого gravo, gravio «предводитель, вождь»: Граф (титул) дворянский титул; «Граф» короткометражная немая кинокомедия Чарли Чаплина (The Count, 1916). От греч. γράφω «царапаю, черчу, пишу»: Граф… … Википедия
Граф зависимостей — В математике, информатике и цифровой электронике, граф зависимостей представляет собой ориентированный граф, отражающий зависимости нескольких объектов друг к другу. По графу зависимостей можно определить порядок вычислений или его недостатки,… … Википедия
Граф объектный — это совокупность узлов и ребер, соединяющих эти узлы. Объектные графы обеспечивают простой способ учета взаимных связей в множестве объектов, и не обязательно, чтобы эти связи в точности проецировались в классические связки объектно… … Википедия
Граф Келли (теория групп) — Граф Кэли граф, который строится по группе с выделенной системой образующих. Назван в честь английского математика Артура Кэли (A. Cayley). Определение Пусть дана дискретная группа G и система образующих S. Предположим S = S − 1, то есть, для… … Википедия
Граф Петерсена — Эту статью следует викифицировать. Пожалуйста, оформите её согласно правилам оформления статей … Википедия
ГРАФ СЛУЧАЙНЫЙ — вероятностная модель, предназначенная для изучения частотных характеристик различных параметров графов. Под Г. с. обычно понимается нек рый класс графов на к ром задано распределение вероятностей. Произвольный конкретный граф Gиз наз. реализацией … Математическая энциклопедия
Граф — Антон (Graf, Anton) 1736, Винтертур 1813, Дрезден. Немецкий живописец. Учился в 1753 1756 у И. У. Шелленберга в Винтертуре, затем у И. Я. Хайда в Аугсбурге. Работал как портретист в Регенсбурге, Винтертуре, Аугсбурге, Мюнхене, Цюрихе. С 1766… … Европейское искусство: Живопись. Скульптура. Графика: Энциклопедия
Объектный граф — Граф объектный это совокупность узлов и ребер, соединяющих эти узлы. Объектные графы обеспечивают простой способ учёта взаимных связей в множестве объектов, и не обязательно, чтобы эти связи в точности проецировались в классические связки… … Википедия
Гамильтонов граф — Граф додекаэдра с выделенным циклом Гамильтона … Википедия
Планарный граф — Планарный граф граф, который может быть изображен на плоскости без пересечения ребер. Более строго: Граф укладывается на некоторой поверхности, если его можно на ней нарисовать без пересечения ребер. Уложенный граф называется геометрическим … Википедия
Теория Графов. Часть 1 Введение и классификация графов
«Графы являются одним из объединяющих понятий информатики – абстрактное представление, которое описывает организацию транспортных систем, взаимодействие между людьми и телекоммуникационные сети. То, что с помощью одного формального представления можно смоделировать так много различных структур, является источником огромной силы для образованного программиста». Стивен С. Скиена
Введение
Сначала под землей города Москвы ничего не было. Потом была построена первая станция метро, а затем и вторая и третья. Образовалось множество станций метро. На карту было занесено множество точек. Позже между станциями стали прокладывать пути линии. И соединилась станция метро А со станцией метро Б. Все остальные станции также стали соединятся друг с другом и на карте появилось множество линий. В итоге мы имеем Московский метрополитен очень красивый, я там был проверял.
Схема Московского метро
Посмотрите какая красота. У нас имеется множество точек (которые называются вершинами или узлами), а также множество линий (называемые рёбрами или дугами). Обозначим множество вершин буквой V от английского vertex−вершина и множество рёбер обозначим E от английского edge−ребро. Граф в формулах именуют буквой G. Все вершины обязательно должны быть идентифицированы.
Отмечу, что число вершин обозначается буквой n:
Число рёбер обозначается буквой m:
Таким образом граф задается и обозначается парой V,E:
Также определение графа рассказывается в этой статье на Хабре (https://habr.com/ru/post/65367/)
Неформально граф является совокупностью точек и линий. Линии в котором задаются парой вершин, расположенных не важно в каком порядке.
Разберем определение графа подробней. Может ли в G быть пустым множество E? Да без проблем! Такой граф будет называться нулевым, а вершины в нем будут называться изолированными.
Нулевой граф
Только вот множество V вершины пустым быть не может. Ведь множество E рёбра задается парой неупорядоченных вершин множества V. Две вершины образующие ребро, называются концами этого ребра.
Множество E задается парой неупорядоченных вершин множества V.
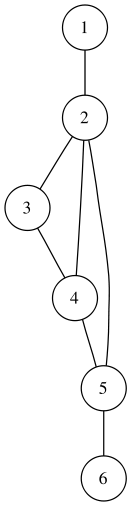
Пример: Пусть множество V = <1,2,3,4,5>. Тогда множество E =
Граф будет выглядеть следующим образом:
Висячей вершиной называется вершина которая соединена только с одной соседней вершиной. В нашем случаи висячей вершиной будет вершина 5, так как она соединена только с вершиной 1.
Степень записывают, как:
Максимальная степень, то есть какое количество степеней вообще присутствуют в графе обозначаются, как:
Формула суммы степеней для G = V,E выглядит так:
То есть сумма степеней всех вершин v графа равна удвоенному количеству его рёбер E. Считаем количество степеней в нашем примере. От этого никуда не денешься. Я насчитал 12. А теперь считаем, сколько у нас рёбер. Их 6! Умножаем на 2 и получаем 12. Совпадение? Не думаю!
А давайте представим наш граф в другом виде, но с сохранением данных пар. G теперь имеет следующий вид:
Заметьте я не изменил пары между собой. Вершина 4 также соединяется с вершиной 3, а у вершины 1 степень также осталась 4. Так почему граф имеет совершенно другой вид и законно ли это?
Классификации графов
Первым признаком классификации является отсутствие или наличие ориентации у ребер.
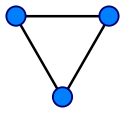
Ребро является неориентированным если у него нет понятия начала или конца. То есть оба его конца равноправны. Такой граф называется неориентированным, обыкновенным или неографом.
Неориентированный граф
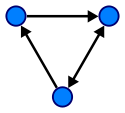
Ориентированное ребро обозначается стрелкой. И указывает ориентацию от вершины к вершине. То есть данный граф имеет начало и конец. И называется он ориентированным или орграфом.
Ориентированный граф
Также существует граф со смешанными ребрами. Это когда в графе присутствуют, как ориентированные рёбра, так и неориентированные.
Смешанный граф
Вторым признаком является отсутствие или наличие кратных ребер.
Мультиграф
Граф в котором кратных ребер нет, является простым графом. В простом графе мы просто называем пару вершин для идентификации ребра, но в мультиграфе такое уже не сработает, так как одна и та же пара вершин будет указывать на два ребра и не понятно что к чему будет относится. Поэтому если вы повстречаете мультиграф, то вы должны обозначить каждое ребро отдельно.
Заключение
В данной стать я не рассмотрел, понятия смежности и инцидентности, однако я решил их рассмотреть в следующий раз. Также хочу отметить, что более подробно виды графов, я буду рассматривать в следующих статьях. Если у вас есть вопросы, предложения или я где-то допустил ошибки, то прошу написать их в комментариях.