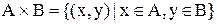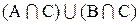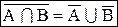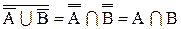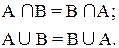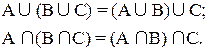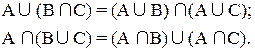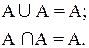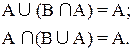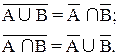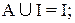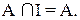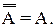Что такое дополнительное множество

Что такое дополнительное множество

2.4. Дополнение множеств. Мощность множеств

Если универсальное множество не указано или оно не ясно из контекста, то говорить о дополнении множества А недопустимо.

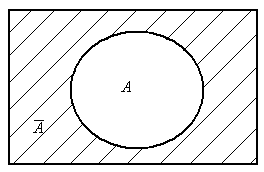
На диаграммах Эйлера универсальное множество I изображается множеством точек некоторого прямоугольника, а его подмножества – в виде кругов внутри этого прямоугольника. Дополнение множества А будет изображено в таком случае той частью прямоугольника, которая лежит за пределами круга (заштрихованная часть рис.2.11).

Для любых подмножеств А и В универсального множества I справедливы следующие утверждения:

1) = А ;

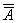
4) А È ( А Ç B )= А, А Ç ( А È B )= А – законы поглощения;

Пусть существует два конечных множества А и В, количество элементов которых N ( A ) и N ( В). Тогда

Эта формула называется формулой включений и исключений и позволяет решать многие задачи теории множеств.

Из (2.4) следует, что если множества А и В не пересекаются, то

Для пересекающихся множеств А и В

N ( A ) + N (В) + N (С) – N (А Ç В) – N ( B Ç C ) – N (А Ç C ) + N (А Ç В Ç C ).

N ( A ) + N (В) + N (С).

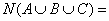
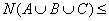
В том случае, когда универсальное для рассматриваемых подмножеств множество I также является конечным, то

N ( I ) – N (А) ;

N ( I ) – N (А È В)= N ( I ) – N ( A ) – N (В) + N (А Ç В).

N ( I ) – N ( A ) – N (В) – N (С) + N (А Ç В)+ N ( B Ç C ) + N (А Ç C )- N (А Ç В Ç C ).

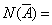
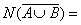
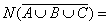
Пример 2.5. В 101 группе – 29 студентов. Каждый из них изучает или английский, или немецкий язык. 5 студентов изучает и английский, и немецкий одновременно. Сколько студентов занимаются в английской группе, если в немецкой – 12 студентов.

Итак N ( А Ç В Ç С Ç D ) ³ 10, т.е. не менее 10 пиратов одновременно лишились и глаза, и уха, и руки, и ноги.

Если каждому элементу множества А можно по некоторому правилу поставить в соответствие один и только один элемент множества В и, наоборот, каждому элементу множества В по некоторому правилу можно поставить в соответствие один и только один элемент множества А, то говорят, что между элементами множеств А и В установлено взаимно-однозначное соответствие. В этом случае множества А и В называют эквивалентными и записывают: А

Очевидно, что равночисленные множества эквивалентны. И, наоборот, два эквивалентных конечных множества равночисленны.

Этот факт является логически чрезвычайно важным, так как для установления равночисленности конечных множеств нет необходимости обладать понятием натурального числа, с помощью которого мы подсчитываем элементы множеств. Напротив, теперь само понятие натурального числа получает новую трактовку: оно есть количественная характеристика, общая всем эквивалентным между собой конечным множествам. Теперь можно, пользуясь только понятиями «множество», «принадлежность», « взаимно-однозначное соответствие» построить всю теорию натуральных чисел.

Рассмотрим теперь бесконечные множества. Для сравнения бесконечных множеств нельзя использовать понятие натурального числа, ибо нельзя пересчитать все элементы таких множеств и поставить им в соответствие натуральное число. Однако их можно сравнивать при помощи понятий « взаимно-однозначное соответствие», «эквивалентность».

N и множество целых отрицательных чисел является счетным.

Если для конечных эквивалентных множеств мы говорили, что они равночисленны, то о бесконечных множествах будем говорить, что они равномощны, т.е. имеют одинаковую мощность. Все эквивалентные бесконечные множества характеризуются их мощностью.

Понятие мощности бесконечного множества аналогично понятию числа конечного множества. Мощность – обобщение понятия «количество» для бесконечных множеств. Оно позволяет сравнивать различные бесконечные множества.

Источник

Дополнение множества

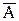
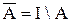
Множество , определяемое из соотношения

1.20

называют дополнением множества А (до универсального множества I)

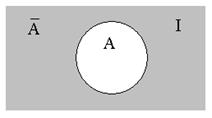
Графически дополнение множества А может быть представлено как показано на рис. 1.5.

Формальное определение дополнения множества А может быть записано как

1.21

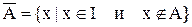
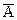
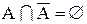
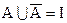
Из определения дополнения множества следует, что А и не имеют общих элементов, т.е.

1.22

Кроме того, 1.23

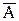
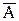
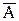
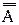
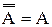
Из симметрии формул 1.22 и 1.23 следует, что не только является дополнением А, но и А является дополнением . Но дополнение есть . Таким образом 1.24

С помощью операции дополнения удобно представить разность множеств:

= , т.е 1.25

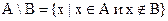
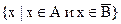
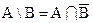
Принцип двойственности в алгебре множеств

В теории множеств и ее приложениях очень важную роль играет принцип двойственности, который основан на следующих двух соотношениях :

1. Дополнение объединений равно пересечению дополнений.

1.26

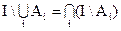
2. Дополнение пересечения равно объединению дополнений.

1.27

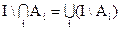
Принцип двойственности состоит в том, что из любого равенства, относящегося к системе подмножеств фиксированного множества I, совершенно автоматически может быть получено другое двойственное равенство путем замены всех рассматриваемых множеств их дополнениями, объединений множеств – пересечениями, а пересечений – объединениями.

Приведем доказательство соотношения 1.26.

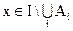
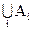
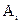
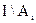
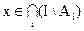
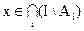
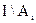
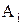
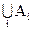
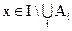
Пусть . Это означает, что х не входит в объединение , т.е. не входит ни в одно из множеств . Следовательно, х принадлежит каждому из дополнений и поэтому . Обратно: пусть , т.е. х входит в каждое . Тогда х не входит ни в одно из множеств , т.е. не принадлежит их объединению , но тогда . Равенство доказано. Аналогично доказывается равенство 1.27.

Тождества алгебры множеств

С помощью операций объединения, пересечения, дополнения из множеств можно составить различные алгебраические выражения. Обозначим через V(A,B,C) некоторое алгебраическое выражение, составленное из множеств А, В, С и представляющее собой некоторое множество.

Пусть W(A,B,C) – другое алгебраическое выражение, составленное из тех же множеств. Если оба алгебраических выражения представляют собой одно и тоже множество, то их можно приравнять друг к другу, получая алгебраическое тождество вида:

Такие тождества очень полезны при преобразовании алгебраических выражений над множествами.

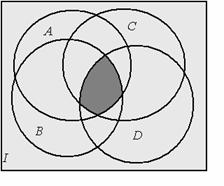
1. Составим диаграммы Эйлера-Венна для выражений:

и

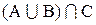
Из диаграмм видно, что оба выражения определяют одно и тоже множество, так что имеет место равенство1:

1.28

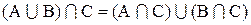
2. Составим диаграммы Эйлера-Венна для выражений

и .

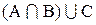
Из построенных диаграмм видно, что они отражают одно и тоже множество, следовательно, между выражениями можно поставить знак равенства:

= 1.29

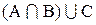
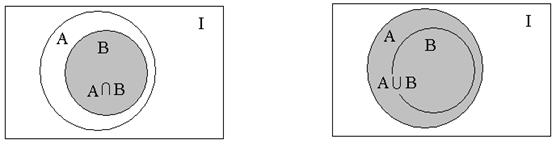
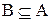
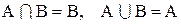
3. Легко убедиться, что если , то

. 1.30

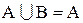
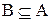
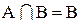
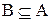
Действительно, все элементы множества В являются в то же время и элементами множества А (т.к. А включает В по определению). Следовательно, пересечение этих множеств, т.е. общая часть множеств А и В совпадает с В. В объединение множеств А и В множество В не внесет ни одного элемента, т.к. каждый элемент множества В является и элементом множества А (по определению), и следовательно . Соответствующие диаграммы Эйлера-Венна приведены на рис. 1.6.

; ;

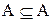
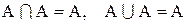
4. Полагая в 1.30 В = А и учитывая, что , получаем:

. 1.31

Установление тождеств алгебры множеств с помощью диаграмм Эйлера-Венна не всегда является удобным. Имеется более общий способ установления тождественности двух алгебраических выражений. Ранее было показано, что множество А равняется множеству В, если .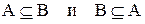

Пусть как и ранее через V(A,B,C) и W(A,B,C) обозначены два алгебраических выражения, получившихся путем применения операций объединения, пересечения и дополнения к множествам А, В, С. Тогда, чтобы доказать, что V=W достаточно показать и что . В свою очередь, чтобы показать, что , нужно убедиться, что из хÎV следует хÎW. Аналогично, чтобы показать, что , нужно убедиться, что из хÎW следует хÎV.

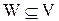
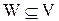
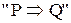
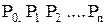
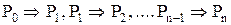
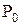
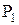
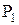
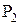
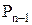
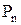
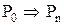
Следует заметить, что каждое из доказательств состоит из последовательности утверждений вида “если P, то Q” (если справедливо P, то справедливо и Q). Для удобства это утверждение записывается как и читается “из P следует Q”. Следовательно, если имеется последовательность такая, что (из следует , из следует , ….. следует ), то имеет место доказательство .

Воспользовавшись этим методом, докажем некоторые тождества.

1. Доказать, что .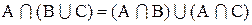

Доказательство:

(Скобки означают, что объединение следует вычислить перед пересечением) . Таким образом . (а)

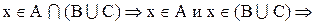
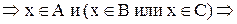
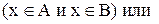
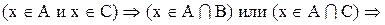
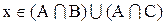
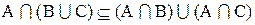
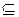
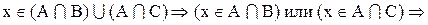
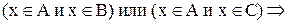
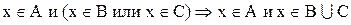
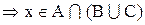
Теперь необходимо доказать включение в обратную сторону:

.

Следовательно, 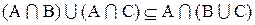. (б)

Тогда на основании полученных выражений (а) и (б) имеет место равенство:

.

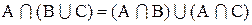
Аналогично доказывается и равенство .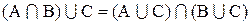

2. Доказать тождество:

. 1.32

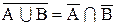
Доказательство:

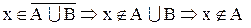
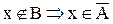
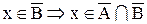
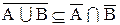
а. и и , т.е. ;

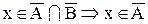
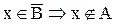
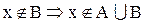
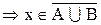
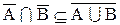
b. и и , т.е. ;

Следовательно, .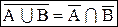

3. Доказать тождество:

. 1.33

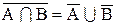
Доказательство:

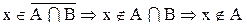
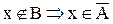
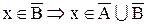
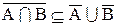
а. и и (или) , т.е. ;

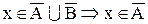
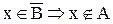
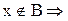
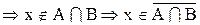
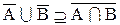
b. или и , т.е ;

Следовательно,

Тождества 1.32 и 1.33 играют важную роль в преобразовании алгебраических выражений алгебры множеств и особенно в математической логике. Их обычно называют тождествами де-Моргана или законами де-Моргана.

Конечно, для доказательств тождеств могут использоваться разные подходы. Докажем, например, тождество 1.33, основываясь на соотношении 1.32 и учитывая 1.24

Итак, необходимо доказать, что .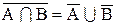

Приведем обе части равенства к одному виду. Выполняя операцию дополнения над обеими частями, получаем:

.

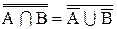
Но, учитывая соотношение 1.24 ( ), .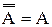

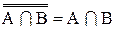
Для правой части на основании 1.32 имеем:

Итак, обе части приведены к одному виду, следовательно, тождество справедливо.

На основании вышеизложенных операций и определений приведем основные законы теории множеств :

1. Законы коммутативности (переместительный закон):

2. Законы ассоциативности (сочетательный закон):

3. Законы дистрибутивности (распределительный закон):

4. Законы идемпотетности:

5. Законы поглощения:

6. Законы де-Моргана:

7. Законы нуля и единицы:

Æ=A; Æ=Æ;

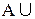
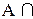
8. Закон двойного дополнения (отрицания):

Разбиение множества

Одной из наиболее часто встречающихся операций над множествами является операция разбиения множества на систему подмножеств.

Примеры:

1. Если N – множество натуральных чисел, а А и В – множества четных и нечетных чисел соответственно, то система будет разбиением множества N. Конечно, множество N можно разбить и на другие подмножества: множества чисел, делящихся на 2, на 3 и т.п.

2. Все множество студентов института можно разбить на отдельные подмножества, представляющие собой множества студентов группы (или факультета).

3. Продукция предприятия (а это есть множество) разбивается на продукцию первого сорта, второго сорта, исправимый брак, неисправимый брак, т.е. – на отдельные подмножества.

Рассмотрим некоторое множество А и систему множеств М = 1, X₂, X₃, …. X_n>.

Определение. Систему множеств М называют разбиением множества А, если удовлетворяются следующие условия:

1. Любое множество Х из М является подмножеством множества А:

.

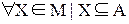
2. Любые два множества X_i и X_j из М являются непересекающимися:

Æ0.

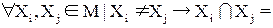
3. Объединение всех множеств, входящих в разбиение, дает множество А:

.

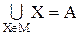
Упорядочение элементов и прямое произведение множеств

Упорядоченное множество

Наряду с понятием множества очень важным понятием является понятие упорядоченного множества или кортежа.

Кортежом называют последовательность элементов (совокупность элементов), в которой каждый элемент занимает определенное место. Сами элементы при этом называют компонентами кортежа (первая компонента, вторая компонента и т.д.).

Примерами кортежей могут быть: множество людей, стоящих в очереди; множество слов в фразе; числа, выражающие долготу и широту точки на местности; параметры, характеризующие состояние какого либо объекта, устройства и т.п.

Любая техническая система часто описывается множеством параметров, принимающих числовые значения. Т.е. система представляется некоторым набором параметров, характеризующих систему – множеством некоторых чисел. При этом устанавливают, какой параметр считать первым, какой вторым и т.д. Т.е. совокупность параметров представляется в виде упорядоченного множества – кортежа.

Число элементов кортежа называют его длиной. Для обозначения кортежа используют круглые скобки. Так, например, X = (x₁, x₂, …. х_n), или X = á x₁, x₂, …. х_n ñ – кортеж длины n c элементами x₁, x₂, …. x_n.

Кортежи длиной 2 называют парами, 3 – тройками, 4 – четверками, n –n-ками. Пустой кортеж обозначается ( ) или символом L. В отличии от обычного множества в кортеже могут быть и одинаковые элементы (два одинаковых слова в фразе, одинаковые числовые значения параметров системы и т.п.).

Упорядоченной парой называется двухэлементное множество, для которого указано, какой элемент является первым, какой – вторым и обозначается ( x₁, x₂)

Если рассматривать упорядоченные множества, элементами которых являются вещественные числа, то такие упорядоченные множества называют точками пространства или векторами. Так, кортеж х₁, х₂ –рассматривается как точка на плоскости или вектор.

х₂ х₁, х₂ Компоненты х₁, х₂ будут проекциями вектора на оси 1 и 2.

х₁ 1

Кортеж (х₁, х₂, х₃) рассматривается как точка в трехмерном пространстве, или как 3-х мерный вектор:

3

x₃ x₁, x₃

x₂, x₃ x₁, x₂, x₃ Если говорить о проекции кортежа сразу на оси, т.е. на координатную плоскость, то нетрудно увидеть, что

x₁ 1 Пр₁₂ (x₁, x₂, x₃) = x₁, x₂;

Обобщая эти понятия, видно, что упорядоченное n-элементное множество вещественных чисел (x₁, x₂, …. x_n) рассматривается как точка в n–мерном пространстве, называемом гиперпространством или n-мерным вектором. При этом, Пр_i (x₁, x₂, …. x_n)=x_i, i= 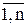1.

Два вектора равны, если они имеют одинаковую длину и их соответствующие компоненты равны, т.е. (a₁, a₂, …a_n) = (b₁, b₂, …b_n) Û «i a_i = b_i.

Прямое произведение множеств

Прямым произведением множеств А и В называют множество, обозначаемое 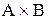и состоящее из всех тех и только тех упорядоченных пар, первая компонента которых принадлежит множеству А, а вторая – множеству В. Таким образом, элементами прямого произведения множеств являются двухэлементные кортежи вида (x,y).

Данное определение может быть записано в виде:

1.34

Источник