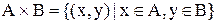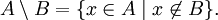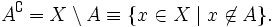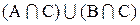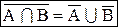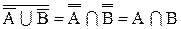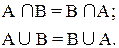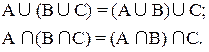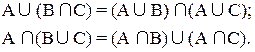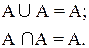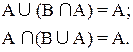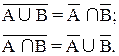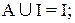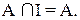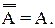Что такое дополнение множества до универсального

Дополнение множества

Дополне́ние в теории множеств — это семейство элементов, не принадлежащих данному множеству.

Содержание

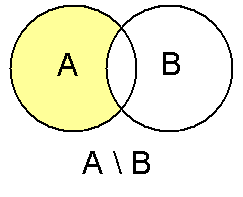
Разность множеств

Определение

Примеры

Свойства

Пусть A,B,C — произвольные множества. Тогда

Компьютерные реализации

Дополнение множества

Определение

Свойства

См. также

Полезное

Смотреть что такое «Дополнение множества» в других словарях:

Дополнение (теория множеств) — Дополнение в теории множеств это семейство элементов, не принадлежащих данному множеству. Содержание 1 Разность множеств 1.1 Определение 1.2 Примеры 1.3 Свойства … Википедия

Дополнение (математика) — Дополнение в теории множеств это семейство элементов, не принадлежащих данному множеству. Содержание 1 Разность множеств 1.1 Определение 1.2 Примеры 1.3 Свойства … Википедия

ДОПОЛНЕНИЕ — операция, к рая ставит в соответствие подмножеству Мданного множества Xдругое подмножество так, что если известны Ми N, то тем или иным способом может быть восстановлено множество X. В зависимости от того, какой структурой наделено множество X,… … Математическая энциклопедия

Дополнение графа — Граф Петерсена (слева) и его дополнение (справа). В теории графов дополнением или обратным к графу G называется такой граф H, имеющий то же множество вершин, что и G, но в котором две несовпадающие вершины смежны тогда и только тогда, когда они… … Википедия

дополнение к множеству — такое множество не А, когда A + не А = 1, где 1 обозначает некоторую предметную область (универсальный класс). Пусть A будет множеством млекопитающих, а областью нашего рассуждения будет множество позвоночных животных. Тогда дополнением к нему… … Словарь терминов логики

ДИЗЪЮНКТНОЕ ДОПОЛНЕНИЕ — множества А множество всех элементов х векторной решетки (векторной структуры) X, дизъюнктных множеству (см. Дизъюнктные элементы). кроме того, если X векторная условно полная решетка, то Add является наименьшей компонентой пространства X,… … Математическая энциклопедия

Плотные и неплотные множества — понятия множеств теории (См. Множеств теория). Множество Е называется плотным на М, если каждая точка множества М является предельной точкой (См. Предельная точка) Е, т. е. в любой окрестности имеются точки, принадлежащие Е. Плотные… … Большая советская энциклопедия

Мера множества — У этого термина существуют и другие значения, см. Мера. Мера множества неотрицательная величина, интуитивно интерпретируемая как размер (объем) множества. Собственно, мера это некоторая числовая функция, ставящая в соответствие каждому… … Википедия

КАТЕГОРИЯ МНОЖЕСТВА — топологическая характеристика массивности множества. Множество Етопологич. пространства Xназ. множеством первой категории на X, если оно представимо в виде конечной или счетной суммы множеств, нигде не плотных на X. В противном случае Еназ.… … Математическая энциклопедия

Существование перечислимого неразрешимого множества — В данной статье будет доказан теорема о существовании перечислимого, но неразрешимого множества. Напомню, что по теореме Поста перечислимое множества разрешимо тогда и только тогда, когда его дополнение перечислимо.Основные определения, такие как … Википедия

Источник

Универсальное множество. Дополнение множества до универсального множества.

Универсальное множество. Дополнение множества до универсального множества.

В конкретных математических областях бывает полезно ввести в рассмотрение столь обширное множество I, что все рассматриваемые множества окажутся его подмножествами. Такое множество I принято называть универсальным множеством или универсумом.Если выбрано некоторое универсальное множество I, то возникает новая теоретико-множественная операция — дополнение. Для всякого множества М (при этом подразумевается, что М — подмножество универсального множества I его дополнение, обозначаемое через М, — это множество всех элементов универсума, которые не принадлежат множеству М:

Таким образом, дополнение — это частный случай разности:

M = I \ M,
все отличие здесь состоит в том, что разность берется относительно фиксированного множества, содержащего все множества, которые в данной связи рассматриваются.

4. Объединение, пересечение и вычитание множеств.

а)Пересечением множеств М и N называют множество тех объектов, которые принадлежат множествам М и N одновременно.

Обозначение: М N = <х|х М и х N>.

б) Объединением множеств М и N называют множество тех элементов, которые содержатся по крайней мере в одном из множеств М или N. Обозначение: M N = <х | х М или х N>.

в) Разностью множеств М и N называют множество тех элементов, которые принадлежат множеству М и не принадлежат множеству N. Обозначение: М \ N. = <х | х М и х N>.

Свойства операций над множествами.

4. Поглощение A U A = A, A n A = A.

5. Существование универсальных границ. А U 0 = A A n 0 = 0 A u U = U A n U = A

6. Двойное дополнение A = A

7. A U A = U A n A = 0

Отношения эквивалентности и порядка.

Решение рекуррентных соотношений. Примеры.

Производящие функции.

Пусть — произвольная (бесконечная) последовательность чисел (целых, рациональных, вещественных или комплексных). Производящей функцией (производящим рядом) называется запись вида Замечание. Не следует думать, что мы можем сказать, чему равно значение производящей функции в точке . Переменная является формальной, и ряд смысла не имеет. Единственное, что мы можем сказать про функцию , это что ее значение в нуле равно . Если, однако, производящий ряд является полиномом (т.е. все его коэффициенты кроме конечного числа равны нулю), то значение этого ряда в любой точке выражается конечной суммой и поэтому имеет смысл.

Маршруты, пути.

32.Матричное задание графов.

Предположим, что все вершины и все ребра неориентиронеориентированного графа или все вершины и все дуги (включая петли) ориентированного графа пронумерованы начиная с единицы.

Граф (неориентированный или ориентированный) может быть представлен в виде матрицы типа nхm, где n — число вершин,a m — число ребер (или дуг). Для неориентированного графа элементы этой матрицы задаются следующим образом: .

Более эффективной матричной структурой, представляющей граф, служит матрица смежности вершин, или булева матрица графа. Это квадратная матрица В порядка n, элементы которой определяют следующим образом:

для неориентированного графа Заметим, что в k-й строке матрицы ориентированного граграфа количество единиц равно полустепени исхода dg+ v_k вершины v_k, а количество единиц в k-м столбце dg- v_k — полустепени захода Для неориентированного графа матрица смежности вершин симметрическая.

Поиск маршрутов в графах.

Алгоритм (Тэрри) поиска пути в связном графе, из вершины vi в вершину vj, где vi vj.

Исходя из вершины vi осуществлять последовательный переход от каждой достигнутой вершины к смежной ей вершине, по следующим правилам:

1. идя по произвольной дуге, всякий раз отмечать направление, в котором оно было пройдено;

2. исходя из некоторой вершины vk, всегда следовать только по дуге, которое не было пройдено или было пройдено в противоположном направлении;

3. для всякой вершины vk, отличной от vi, отмечать первую заходящую в vk дугу, если вершина vk встречается в первый раз;

4. исходя из некоторой вершины, vk, отличной от вершины vi, по первой заходящей в vk дуге идти лишь тогда, когда нет других возможностей.

Эйлеровы графы и циклы.

Эйлеровым путем в графе называется путь, содержащий все ребра графа. Эйлеровым циклом в графе называется цикл, содержащий все ребра графа. Связный граф называется эйлеровым, если существует замкнутая цепь, проходящая через каждое его ребро. Такая цепь называется эйлеровой цепью. Отметим, что в этом определении требуется, чтобы каждое ребро проходилось только один раз. Если снять ограничение на замкнутость цепи, то граф называется полуэйлеровым, при этом каждый эйлеров граф будет полуэйлеровым. Если граф обладает эйлеровым циклом, то он является связным, а все его вершины — четными.

39. Гамильтоновы графы и циклы.

Планарные графы.

Граф называется плоским, если никакие два его ребра не пересекаются. Граф называется планарным, если он изоморфен некоторому плоскому графу. Любой планарный граф допускает плоское представление, в котором все ребра являются отрезками. Любой граф укладывается в трехмерном пространстве , т.е. любой граф можно изобразить в трехмерном пространстве так, чтобы его ребра не пересекались.

Принцип Дирихле.

Самая популярная формулировка принципа Дирихле такова: «Если в n клетках сидит m зайцев, причем m > n, то хотя бы в одной клетке сидят по крайней мере два зайца». На первый взгляд даже непонятно, почему это совершенно очевидное замечание является весьма эффективным методом решения задач. Дело в том, что в каждой конкретной задаче нелегко бывает понять, что же здесь «зайцы» и «клетки» и почему зайцев больше, чем клеток. Выбор зайцев и клеток часто неочевиден; далеко не всегда по виду задачи можно определить, что следует воспользоваться принципом Дирихле. А главное, этот метод дает неконструктивное доказательство (мы, естественно, не можем сказать, в какой именно клетке сидят два зайца, а знаем только, что такая клетка есть), а попытка дать конструктивное доказательство, т. е. доказательство путем явного построения или указания требуемого объекта, может привести к гораздо большим трудностям. Некоторые задачи решаются также методами, в какой-то мере аналогичными принципу Дирихле. Сформулируем соответствующие утверждения (все они легко доказываются методом от противного).

а) Если на отрезке длиной 1 расположено несколько отрезков. сумма длин которых больше 1, то по крайней мере два из них имеют общую точку.

б) Если на окружности радиуса 1 расположено несколько дуг, сумма длин которых больше 2, то по крайней мере две из них имеют общую точку.

в) Если внутри фигуры площадью 1 расположено несколько фигур, сумма площадей которых больше 1, то по крайней мере две из них имеют общую точку.

44.Сущность теории Рамсея. Теорема Рамсея. Числа Рамсея.

Теорема Рамсея гарантирует существование чисел Рамсея для любых k и m. Таким образом можно говорить о содержании в бесконечном графе высокоорганизованной структуры любой сложности. Но об этом позже (быть может). А пока хочется остановиться на числах Рамсея. Для удобства перефразируем определение: Число Рамсея R(k, m) это наименьшее число n такое, что в любом полном графе с n вершинами, ребра которого раскрашены в красный и синий цвета, найдется либо подграф с k вершинами, все ребра которого окрашены в красный цвет, либо подграф с m вершинами, все ребра которого окрашены в синий цвет. Чтобы понять сложность вычисления чисел Рамсея, то следует отметить что число R(5, 5) до сих пор не найдено. Можно заметить три очевидных факта, касающихся чисел Рамсея:
1. R(k, m) = R(m, k)
2. R(1, m) = 1
3. R(2, m) = m
Остальные числа вычисляются индивидуально.

Приложение теоремы Рамсея. Теорема Ван дер Вардена.

Головоломка о вечеринке представляет собой задачу, типичную для приложений теории Рамсея. Какое количество людей достаточно для того, чтобы образовать группу, в которой всегда окажется либо четверо людей знакомых друг с другом, либо четверо, друг с другом незнакомых? На этом рисунке гости представлены точками. Каждое красное ребро на этом графе соединяет гостей, знакомых друг с другом, а каждое синее — незнакомых. В группе из 17 точек, изображённых на рисунке, невозможно найти четыре точки для которых сеть соединяющих их рёбер была бы целиком красной или целиком синей Поэтому требуется более 17 человек, чтобы среди них обязательно оказалось либо четверо знакомых, либо четверо незнакомых друг с другом. На самом деле во всякой группе из 18 человек всегда найдутся либо четверо знакомых, либо четверо незнакомых друг с другом. Если множество всех натуральных чисел любым способом разбито на конечное число классов, то хотя бы один из этих классов содержит сколь угодно длинную арифметическую прогрессии.

Этот удивительный по простоте формулировки и очень нетривиальный по доказательству результат выдающийся российский математик и педагог Александр Яковлевич Хинчин (19.07.1894-18.11.1959) назвал одной из жемчужин теории чисел. Знаменитая теорема Ван дер Вардена утверждает, что для любых натуральных чисел n>2, r>1 найдется такое минимальное натуральное число W(n,r), что в любой раскраске множества натуральных чисел <1. W(n,r)>в r цветов найдется одноцветная арифметическая прогрессия длины n. Величину W(n,r) из теоремы Ван дер Вардена принято называть функцией Ван дер Вардена.

Универсальное множество. Дополнение множества до универсального множества.

В конкретных математических областях бывает полезно ввести в рассмотрение столь обширное множество I, что все рассматриваемые множества окажутся его подмножествами. Такое множество I принято называть универсальным множеством или универсумом.Если выбрано некоторое универсальное множество I, то возникает новая теоретико-множественная операция — дополнение. Для всякого множества М (при этом подразумевается, что М — подмножество универсального множества I его дополнение, обозначаемое через М, — это множество всех элементов универсума, которые не принадлежат множеству М:

Таким образом, дополнение — это частный случай разности:

M = I \ M,
все отличие здесь состоит в том, что разность берется относительно фиксированного множества, содержащего все множества, которые в данной связи рассматриваются.

4. Объединение, пересечение и вычитание множеств.

а)Пересечением множеств М и N называют множество тех объектов, которые принадлежат множествам М и N одновременно.

Обозначение: М N = <х|х М и х N>.

б) Объединением множеств М и N называют множество тех элементов, которые содержатся по крайней мере в одном из множеств М или N. Обозначение: M N = <х | х М или х N>.

в) Разностью множеств М и N называют множество тех элементов, которые принадлежат множеству М и не принадлежат множеству N. Обозначение: М \ N. = <х | х М и х N>.

Свойства операций над множествами.

4. Поглощение A U A = A, A n A = A.

5. Существование универсальных границ. А U 0 = A A n 0 = 0 A u U = U A n U = A

6. Двойное дополнение A = A

7. A U A = U A n A = 0

Источник

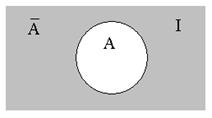
Дополнение множества

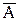
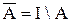
Множество , определяемое из соотношения

1.20

называют дополнением множества А (до универсального множества I)

Графически дополнение множества А может быть представлено как показано на рис. 1.5.

Формальное определение дополнения множества А может быть записано как

1.21

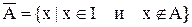
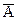
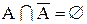
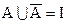
Из определения дополнения множества следует, что А и не имеют общих элементов, т.е.

1.22

Кроме того, 1.23

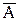
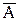
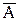
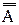
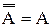
Из симметрии формул 1.22 и 1.23 следует, что не только является дополнением А, но и А является дополнением . Но дополнение есть . Таким образом 1.24

С помощью операции дополнения удобно представить разность множеств:

= , т.е 1.25

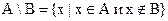
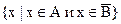
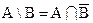
Принцип двойственности в алгебре множеств

В теории множеств и ее приложениях очень важную роль играет принцип двойственности, который основан на следующих двух соотношениях :

1. Дополнение объединений равно пересечению дополнений.

1.26

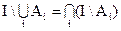
2. Дополнение пересечения равно объединению дополнений.

1.27

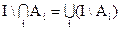
Принцип двойственности состоит в том, что из любого равенства, относящегося к системе подмножеств фиксированного множества I, совершенно автоматически может быть получено другое двойственное равенство путем замены всех рассматриваемых множеств их дополнениями, объединений множеств – пересечениями, а пересечений – объединениями.

Приведем доказательство соотношения 1.26.

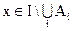
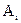
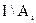
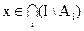
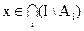
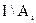
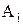
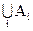
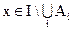
Пусть . Это означает, что х не входит в объединение , т.е. не входит ни в одно из множеств . Следовательно, х принадлежит каждому из дополнений и поэтому . Обратно: пусть , т.е. х входит в каждое . Тогда х не входит ни в одно из множеств , т.е. не принадлежит их объединению , но тогда . Равенство доказано. Аналогично доказывается равенство 1.27.

Тождества алгебры множеств

С помощью операций объединения, пересечения, дополнения из множеств можно составить различные алгебраические выражения. Обозначим через V(A,B,C) некоторое алгебраическое выражение, составленное из множеств А, В, С и представляющее собой некоторое множество.

Пусть W(A,B,C) – другое алгебраическое выражение, составленное из тех же множеств. Если оба алгебраических выражения представляют собой одно и тоже множество, то их можно приравнять друг к другу, получая алгебраическое тождество вида:

Такие тождества очень полезны при преобразовании алгебраических выражений над множествами.

1. Составим диаграммы Эйлера-Венна для выражений:

и

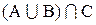
Из диаграмм видно, что оба выражения определяют одно и тоже множество, так что имеет место равенство1:

1.28

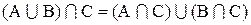
2. Составим диаграммы Эйлера-Венна для выражений

и .

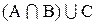
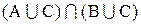
Из построенных диаграмм видно, что они отражают одно и тоже множество, следовательно, между выражениями можно поставить знак равенства:

= 1.29

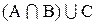
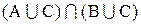
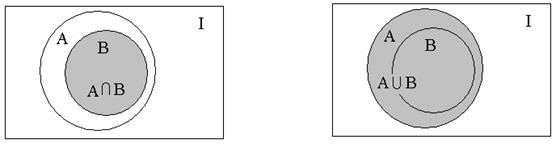
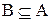
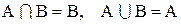
3. Легко убедиться, что если , то

. 1.30

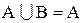
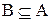
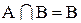
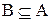
Действительно, все элементы множества В являются в то же время и элементами множества А (т.к. А включает В по определению). Следовательно, пересечение этих множеств, т.е. общая часть множеств А и В совпадает с В. В объединение множеств А и В множество В не внесет ни одного элемента, т.к. каждый элемент множества В является и элементом множества А (по определению), и следовательно . Соответствующие диаграммы Эйлера-Венна приведены на рис. 1.6.

; ;

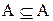
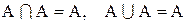
4. Полагая в 1.30 В = А и учитывая, что , получаем:

. 1.31

Установление тождеств алгебры множеств с помощью диаграмм Эйлера-Венна не всегда является удобным. Имеется более общий способ установления тождественности двух алгебраических выражений. Ранее было показано, что множество А равняется множеству В, если .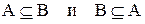

Пусть как и ранее через V(A,B,C) и W(A,B,C) обозначены два алгебраических выражения, получившихся путем применения операций объединения, пересечения и дополнения к множествам А, В, С. Тогда, чтобы доказать, что V=W достаточно показать и что . В свою очередь, чтобы показать, что , нужно убедиться, что из хÎV следует хÎW. Аналогично, чтобы показать, что , нужно убедиться, что из хÎW следует хÎV.

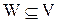
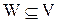
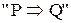
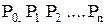
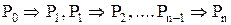
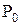
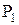
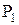
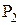
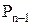
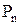
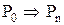
Следует заметить, что каждое из доказательств состоит из последовательности утверждений вида “если P, то Q” (если справедливо P, то справедливо и Q). Для удобства это утверждение записывается как и читается “из P следует Q”. Следовательно, если имеется последовательность такая, что (из следует , из следует , ….. следует ), то имеет место доказательство .

Воспользовавшись этим методом, докажем некоторые тождества.

1. Доказать, что .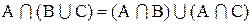

Доказательство:

(Скобки означают, что объединение следует вычислить перед пересечением) . Таким образом . (а)

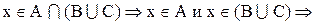
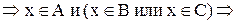
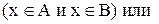
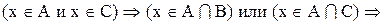
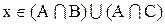
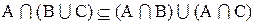
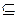
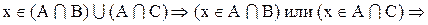
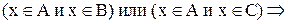
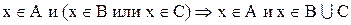
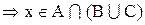
Теперь необходимо доказать включение в обратную сторону:

.

Следовательно, 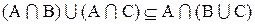. (б)

Тогда на основании полученных выражений (а) и (б) имеет место равенство:

.

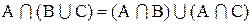
Аналогично доказывается и равенство .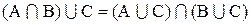

2. Доказать тождество:

. 1.32

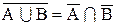
Доказательство:

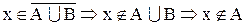
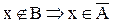
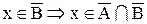
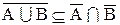
а. и и , т.е. ;

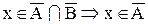
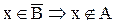
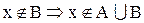
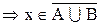
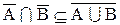
b. и и , т.е. ;

Следовательно, .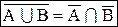

3. Доказать тождество:

. 1.33

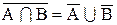
Доказательство:

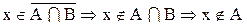
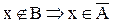
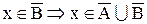
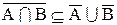
а. и и (или) , т.е. ;

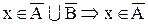
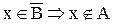
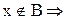
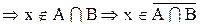
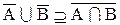
b. или и , т.е ;

Следовательно,

Тождества 1.32 и 1.33 играют важную роль в преобразовании алгебраических выражений алгебры множеств и особенно в математической логике. Их обычно называют тождествами де-Моргана или законами де-Моргана.

Конечно, для доказательств тождеств могут использоваться разные подходы. Докажем, например, тождество 1.33, основываясь на соотношении 1.32 и учитывая 1.24

Итак, необходимо доказать, что .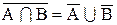

Приведем обе части равенства к одному виду. Выполняя операцию дополнения над обеими частями, получаем:

.

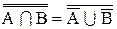
Но, учитывая соотношение 1.24 ( ), .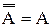

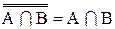
Для правой части на основании 1.32 имеем:

Итак, обе части приведены к одному виду, следовательно, тождество справедливо.

На основании вышеизложенных операций и определений приведем основные законы теории множеств :

1. Законы коммутативности (переместительный закон):

2. Законы ассоциативности (сочетательный закон):

3. Законы дистрибутивности (распределительный закон):

4. Законы идемпотетности:

5. Законы поглощения:

6. Законы де-Моргана:

7. Законы нуля и единицы:

Æ=A; Æ=Æ;

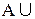
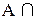
8. Закон двойного дополнения (отрицания):

Разбиение множества

Одной из наиболее часто встречающихся операций над множествами является операция разбиения множества на систему подмножеств.

Примеры:

1. Если N – множество натуральных чисел, а А и В – множества четных и нечетных чисел соответственно, то система будет разбиением множества N. Конечно, множество N можно разбить и на другие подмножества: множества чисел, делящихся на 2, на 3 и т.п.

2. Все множество студентов института можно разбить на отдельные подмножества, представляющие собой множества студентов группы (или факультета).

3. Продукция предприятия (а это есть множество) разбивается на продукцию первого сорта, второго сорта, исправимый брак, неисправимый брак, т.е. – на отдельные подмножества.

Рассмотрим некоторое множество А и систему множеств М = 1, X₂, X₃, …. X_n>.

Определение. Систему множеств М называют разбиением множества А, если удовлетворяются следующие условия:

1. Любое множество Х из М является подмножеством множества А:

.

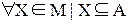
2. Любые два множества X_i и X_j из М являются непересекающимися:

Æ0.

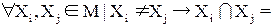
3. Объединение всех множеств, входящих в разбиение, дает множество А:

.

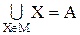
Упорядочение элементов и прямое произведение множеств

Упорядоченное множество

Наряду с понятием множества очень важным понятием является понятие упорядоченного множества или кортежа.

Кортежом называют последовательность элементов (совокупность элементов), в которой каждый элемент занимает определенное место. Сами элементы при этом называют компонентами кортежа (первая компонента, вторая компонента и т.д.).

Примерами кортежей могут быть: множество людей, стоящих в очереди; множество слов в фразе; числа, выражающие долготу и широту точки на местности; параметры, характеризующие состояние какого либо объекта, устройства и т.п.

Любая техническая система часто описывается множеством параметров, принимающих числовые значения. Т.е. система представляется некоторым набором параметров, характеризующих систему – множеством некоторых чисел. При этом устанавливают, какой параметр считать первым, какой вторым и т.д. Т.е. совокупность параметров представляется в виде упорядоченного множества – кортежа.

Число элементов кортежа называют его длиной. Для обозначения кортежа используют круглые скобки. Так, например, X = (x₁, x₂, …. х_n), или X = á x₁, x₂, …. х_n ñ – кортеж длины n c элементами x₁, x₂, …. x_n.

Кортежи длиной 2 называют парами, 3 – тройками, 4 – четверками, n –n-ками. Пустой кортеж обозначается ( ) или символом L. В отличии от обычного множества в кортеже могут быть и одинаковые элементы (два одинаковых слова в фразе, одинаковые числовые значения параметров системы и т.п.).

Упорядоченной парой называется двухэлементное множество, для которого указано, какой элемент является первым, какой – вторым и обозначается ( x₁, x₂)

Если рассматривать упорядоченные множества, элементами которых являются вещественные числа, то такие упорядоченные множества называют точками пространства или векторами. Так, кортеж х₁, х₂ –рассматривается как точка на плоскости или вектор.

х₂ х₁, х₂ Компоненты х₁, х₂ будут проекциями вектора на оси 1 и 2.

х₁ 1

Кортеж (х₁, х₂, х₃) рассматривается как точка в трехмерном пространстве, или как 3-х мерный вектор:

3

x₃ x₁, x₃

x₂, x₃ x₁, x₂, x₃ Если говорить о проекции кортежа сразу на оси, т.е. на координатную плоскость, то нетрудно увидеть, что

x₁ 1 Пр₁₂ (x₁, x₂, x₃) = x₁, x₂;

Обобщая эти понятия, видно, что упорядоченное n-элементное множество вещественных чисел (x₁, x₂, …. x_n) рассматривается как точка в n–мерном пространстве, называемом гиперпространством или n-мерным вектором. При этом, Пр_i (x₁, x₂, …. x_n)=x_i, i= 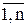1.

Два вектора равны, если они имеют одинаковую длину и их соответствующие компоненты равны, т.е. (a₁, a₂, …a_n) = (b₁, b₂, …b_n) Û «i a_i = b_i.

Прямое произведение множеств

Прямым произведением множеств А и В называют множество, обозначаемое 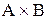и состоящее из всех тех и только тех упорядоченных пар, первая компонента которых принадлежит множеству А, а вторая – множеству В. Таким образом, элементами прямого произведения множеств являются двухэлементные кортежи вида (x,y).

Данное определение может быть записано в виде:

1.34

Источник