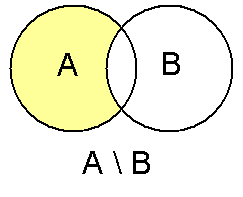
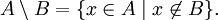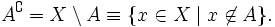Что такое дополнение множеств в математике

Дополнение (математика)

Дополне́ние в теории множеств — это семейство элементов, не принадлежащих данному множеству.

Содержание

Разность множеств

Определение

Примеры

Свойства

Пусть A,B,C — произвольные множества. Тогда

Компьютерные реализации

Дополнение множества

Определение

Свойства

См. также

Полезное

Смотреть что такое «Дополнение (математика)» в других словарях:

Математика исламского средневековья — Данная статья часть обзора История математики. Арабский халифат (750 г.) Математика Востока, в отличие от древнегреческой математики, в … Википедия

Двойственность (математика) — Принцип, формулируемый в некоторых разделах математики и заключающийся в том, что каждому верному утверждению этого раздела отвечает двойственное утверждение, которое может быть получено из первого путём замены входящих в него понятий на другие,… … Википедия

Техническое образование (дополнение к статье) — В области высшего Т. образования в 1900 1907 гг. состоялись следующие важнейшие узаконения. 12 июня 1900 г. утверждено положение о Томском технологическом институте; помимо обычных отделений химического и механического в его составе открыты еще… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Ванновский (дополнение к статье) — (Петр Семенович) 1 января 1898 г. по болезни оставил пост военного министра и назначен членом государственного совета. В 1899 г. (20 февраля) В. было поручено всестороннее расследование причин беспорядков, происшедших в различных высших учебных… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Школы сельскохозяйственные (дополнение к статье) — 26 мая 1904 г. утверждено новое положение о сельскохозяйственном образовании, определяющее лишь общие основания для устройства с. х. учебных заведений, а министру земледелия и государственных имуществ предоставляющее издавать уставы, определяющие … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Область (математика) — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш … Википедия

Путь (математика) — Кривая или линия геометрическое понятие, определяемое в разных разделах геометрии различно. Содержание 1 Элементарная геометрия 2 Параметрические определения 3 Кривая Жордана … Википедия

Комплекс (математика) — У этого термина существуют и другие значения, см. Комплекс. Комплекс[1] (от лат. compléxus связь, сочетание) одно из основных понятий комбинаторной топологии. Комплексом называется частично упорядоченное правильным, рефлексивным… … Википедия

Пуанкаре, Анри — Анри Пуанкаре Henri Poincaré Дата рождения: 29 апреля 1854(1854 04 29) Место рождения: Нанси … Википедия

SAT — У этого термина существуют и другие значения, см. SAT (значения). SAT Reasoning Test (а также «Scholastic Aptitude Test» и «Scholastic Assessment Test», дословно «Школьный Оценочный Тест») стандартизованный тест для приема в высшие учебные… … Википедия

Источник

Дополнение (теория множеств)

Дополне́ние в теории множеств — это семейство элементов, не принадлежащих данному множеству.

Содержание

Разность множеств

Определение

Примеры

Свойства

Пусть A,B,C — произвольные множества. Тогда

Компьютерные реализации

Дополнение множества

Определение

Свойства

См. также

Полезное

Смотреть что такое «Дополнение (теория множеств)» в других словарях:

Теория множеств — Теория множеств раздел математики, в котором изучаются общие свойства множеств. Теория множеств лежит в основе большинства математических дисциплин; она оказала глубокое влияние на понимание предмета самой… … Википедия

Наивная теория множеств — Теория множеств раздел математики, в котором изучаются общие свойства множеств. Теория множеств лежит в основе большинства математических дисциплин; она оказала глубокое влияние на понимание предмета самой математики. Содержание 1 Теория… … Википедия

Описательная теория множеств — Теория множеств раздел математики, в котором изучаются общие свойства множеств. Теория множеств лежит в основе большинства математических дисциплин; она оказала глубокое влияние на понимание предмета самой математики. Содержание 1 Теория… … Википедия

ДЕСКРИПТИВНАЯ ТЕОРИЯ МНОЖЕСТВ — раздел теории множеств, изучающий внутреннее строение множеств в зависимости ют тех операций, при помощи к рых эти множества могут быть построены из множеств сравнительно простой природы (напр., замкнутых или открытых подмножеств данного… … Математическая энциклопедия

Алгебра (теория множеств) — У этого термина существуют и другие значения, см. Алгебра (значения). Алгебра множеств в теории множеств это непустая система подмножеств, замкнутая относительно операций дополнения (разности) и объединения (суммы). Содержание 1 Определение … Википедия

РЕКУРСИВНАЯ ТЕОРИЯ МНОЖЕСТВ — раздел тео рии рекурсивных функций, в к ром рассматриваются и классифицируются подмножества натуральных чисел с алгоритмич. точки зрения, а также исследуются структуры, возникающие в результате такой классификации. Для каждого множества А, к рое… … Математическая энциклопедия

Принцип двойственности (теория множеств) — У этого термина существуют и другие значения, см. Принцип двойственности. Принцип двойственности в абстрактной теории множеств. Пусть дано множество М. Рассмотрим систему всех его подмножеств А, В, С и т. д. Справедливо следующее предложение:… … Википедия

Дополнение — В Викисловаре есть статья «дополнение» Дополнение может означать … Википедия

Теория моделей — Теория моделей раздел математической логики, который занимается изучением связи между формальными языками и их интерпретациями, или моделями. Название теория моделей было впервые предложено Тарским в 1954 году. Основное развитие теория … Википедия

МНОЖЕСТВ ТЕОРИЯ — Под множеством понимается совокупность каких либо объектов, называемых элементами множества. Теория множеств занимается изучением свойств как произвольных множеств, так и множеств специального вида независимо от природы образующих их элементов.… … Энциклопедия Кольера

Источник

Дополнение множества

Дополне́ние в теории множеств — это семейство элементов, не принадлежащих данному множеству.

Содержание

Разность множеств

Определение

Примеры

Свойства

Пусть A,B,C — произвольные множества. Тогда

Компьютерные реализации

Дополнение множества

Определение

Свойства

См. также

Полезное

Смотреть что такое «Дополнение множества» в других словарях:

Дополнение (теория множеств) — Дополнение в теории множеств это семейство элементов, не принадлежащих данному множеству. Содержание 1 Разность множеств 1.1 Определение 1.2 Примеры 1.3 Свойства … Википедия

Дополнение (математика) — Дополнение в теории множеств это семейство элементов, не принадлежащих данному множеству. Содержание 1 Разность множеств 1.1 Определение 1.2 Примеры 1.3 Свойства … Википедия

ДОПОЛНЕНИЕ — операция, к рая ставит в соответствие подмножеству Мданного множества Xдругое подмножество так, что если известны Ми N, то тем или иным способом может быть восстановлено множество X. В зависимости от того, какой структурой наделено множество X,… … Математическая энциклопедия

Дополнение графа — Граф Петерсена (слева) и его дополнение (справа). В теории графов дополнением или обратным к графу G называется такой граф H, имеющий то же множество вершин, что и G, но в котором две несовпадающие вершины смежны тогда и только тогда, когда они… … Википедия

дополнение к множеству — такое множество не А, когда A + не А = 1, где 1 обозначает некоторую предметную область (универсальный класс). Пусть A будет множеством млекопитающих, а областью нашего рассуждения будет множество позвоночных животных. Тогда дополнением к нему… … Словарь терминов логики

ДИЗЪЮНКТНОЕ ДОПОЛНЕНИЕ — множества А множество всех элементов х векторной решетки (векторной структуры) X, дизъюнктных множеству (см. Дизъюнктные элементы). кроме того, если X векторная условно полная решетка, то Add является наименьшей компонентой пространства X,… … Математическая энциклопедия

Плотные и неплотные множества — понятия множеств теории (См. Множеств теория). Множество Е называется плотным на М, если каждая точка множества М является предельной точкой (См. Предельная точка) Е, т. е. в любой окрестности имеются точки, принадлежащие Е. Плотные… … Большая советская энциклопедия

Мера множества — У этого термина существуют и другие значения, см. Мера. Мера множества неотрицательная величина, интуитивно интерпретируемая как размер (объем) множества. Собственно, мера это некоторая числовая функция, ставящая в соответствие каждому… … Википедия

КАТЕГОРИЯ МНОЖЕСТВА — топологическая характеристика массивности множества. Множество Етопологич. пространства Xназ. множеством первой категории на X, если оно представимо в виде конечной или счетной суммы множеств, нигде не плотных на X. В противном случае Еназ.… … Математическая энциклопедия

Существование перечислимого неразрешимого множества — В данной статье будет доказан теорема о существовании перечислимого, но неразрешимого множества. Напомню, что по теореме Поста перечислимое множества разрешимо тогда и только тогда, когда его дополнение перечислимо.Основные определения, такие как … Википедия

Источник

Равенство множеств. Подмножество. Универсальное множество. Дополнение множества

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

ОСНОВНЫЕ ДАННЫЕ О РАБОТЕ

В обычной речи мы часто употребляем слово “множество”: множество людей, множество книг, множество законов, множество денег и т.д.

В математике множеством называют совокупность, набор каких-либо предметов (объектов). Это не есть точное математическое определение. Так же, как и понятия точки, числа и т.д., понятие множества является одним из тех первоначальных, наиболее общих понятий, которые приходится принимать без определения.

Примерами пустых множеств могут служить:

а) множество действительных чисел, являющихся корнями уравнения x 2 + 1 = 0;

б) множество треугольников, сумма углов которых отлична от 180°;

в) множество решений системы уравнений

.

В каком случае можно считать, что множество задано? Иногда можно задать множество, перечислив все его элементы. Например, множество учеников в классе задается перечислением фамилий в классном журнале. Это нетрудно сделать, так как такое множество содержит конечное число элементов. Однако не всякое конечное множество можно задать перечислением. Множества слонов на нашей планете или рыб в океане тоже конечные, но попробуйте их перечислить
(или пересчитать!)! Тем более нельзя перечислить все элементы бесконечного множества. Так, множество всех цифр конечное и их легко перечислить: А=<0,1,2,3,4,5,6,7,8,9>. А вот множество всех целых чисел, составленных из этих цифр, бесконечное и их уже не перечислишь. В таких случаях множество считается заданным, если указано некоторое свойство, которым обладают все его элементы и не обладают никакие другие объекты. Такое свойство называется характерис-тическим свойством множества. Одно и то же множество может быть задано различными характеристическими свойствами. Например, множество <2,4>может быть задано как:

а) множество четных чисел, удовлетворяющих неравенству 1

1.2. Равенство множеств. Подмножество. Универсальное множество. Дополнение множества

Приведем примеры подмножеств:

а) множество учеников 10-го класса данной школы есть подмножество множества всех учеников этой школы;

б) множество жителей Москвы является подмножеством множества жителей России;

в) множество всех квадратов есть подмножество множества всех прямоугольников;

г) множество Z всех целых чисел есть подмножество множества Q всех рациональных чисел.

Если одновременно с отношением А  В имеет место отношение В  А, то А=В. То есть, если одновременно А есть подмножество В и В есть подмножество А, то такие два множества равны.

Отношение А  В изображено с помощью диаграмм на рис. 2 а, б.

1.3. Операции над множествами: объединение, пересечение, разность

в) Обозначим через А множество целых чисел, через В множество четных чисел. Тогда А  В есть множество А, то есть А  В=А.

Примеры. а) Термин “пересечение” по существу геометрического происхождения. Пересечением прямой и плоскости, если прямая не параллельна плоскости, является их единственная общая точка. Если прямая и плоскость параллельны, то пересечение этих множеств пусто. Если же прямая лежит на плоскости, то их пересечение совпадает с множеством точек этой прямой.

Множество делителей числа 72 конечно. А множество кратных этого числа бесконечно: С=<72,144,216. 72n. >.

Бесконечно и множество кратных числа 54: D=<54,108,162,216. 54m. >.

Пересечением этих множеств является множество общих кратных для чисел 72 и 54: С  D=<216,432. >.

Наименьшее число в С  D, то есть 216, называется наименьшим общим кратным для 72 и 54.

Рис. 8 Рис. 9 Рис. 10

в) Разностью множества четных чисел и множества целых чисел является пустое множество.

1.4. Основные законы операций над множествами

Некоторые свойства объединения и пересечения множеств очень похожи на свойства хорошо известных алгебраических операций сложения и умножения. Вместе с тем многие свойства введенных операций над множествами отличаются от свойств алгебраических операций. Приведем здесь основные свойства:

Здесь роль пустого множества аналогична роли числа 0 в алгебре. Однако свойство  \А=  уже не имеет аналога в алгебре.

Первый распределительный закон аналогичен соответствую­щему распределительному закону в алгебре. А вот второй закон никакого аналога в алгебре не имеет.

Свойства, сформулированные в п.п.1-4, очевидны и не нуждаются в доказательстве. Распределительные законы в п.5 уже сложнее. Однако вместо того, чтобы их строго доказывать, лучше попытаться их понять, пользуясь диаграммами Венна.

1.5. Числовые множества. Множества точек на прямой,
задаваемые алгебраическими уравнениями и неравенствами

а) множество всех действительных чисел R;

б) множество всех рациональных чисел Q;

в) множество всех натуральных чисел N;

г) множество всех чисел вида , где n принимает все натуральные значения.

Заштрихованная часть числовой прямой содержит все точки, принад­лежащие соответст-вующему интервалу. Незакрашенные кружочки означают, что эти точки не принадлежат интервалу, а закрашенные, наоборот, означают, что эти точки принадлежат интервалу.

2. Окрестность точки. Окрестностью точки x ₀ называется любой открытый интервал, содержащий эту точку (рис. 15). Открытый интервал (a,b) служит окрестностью всякой принад-лежащей ему точки.

Пример 1. Уравнение имеет своей областью определения множество [-4,+  ). Найдем его корни. Возведем обе части уравнения в квадрат:

x + 4 = (2 – x ) 2 или x 2 – 5 x = 0.

Решим полученное квадратное уравнение:

x ( x – 5) = 0 или x ₁ = 0, x ₂ = 5.

Оба числа x ₁ = 0 и x ₂ = 5 принадлежат множеству [-4,+  ), однако число x ₂ = 5 является посторонним корнем уравнения (это показывает простая проверка: ). Таким образом множество корней данного уравнения <0> [-4,+  ). На прямой эти множества изображаются так:

.

Поэтому данное уравнение можно представить в виде совокупности двух уравнений: х = 3 и
–х = 3. Откуда получим два корня x ₁ = 3, x ₂ = –3. Геометрически эти решения можно истолковать так: расстояние от x ₁ до начала отсчета О и расстояние x ₂ до начала отсчета О равны 3 (рис. 17).

Пример 3. Неравенство | x | x |

4. Системы уравнений и неравенств с одним неизвестным.

Пример 5. Решить систему уравнений

.

или x ₁ = 3, x ₂ = –1.

При решении второго уравнения надо указать вначале его область определения: x  3. Далее, приравняв каждый из множителей нулю и решив получившиеся уравнения, будем иметь x ₁ = 3,
x ₂ = –2. Число x ₂ = –2 не принадлежит области определения [3,+  ) и является посторонним корнем. Следовательно, система уравнений имеет единственное решение: <3>.

Пример 6. Решить систему неравенств:

.

x 2 – 5 x – 6 = ( x + 1) ( x – 6).

Пересечением множеств является множество точек, на котором штриховки накладываются друг на друга.

Учитывая рассмотренные примеры 5 и 6, можно сделать один вывод. Множество решений системы уравнений или неравенств представляет собой пересечение множеств решений каждого из уравнений или неравенств, входящих в эту систему.

Иногда в процессе решения системы уравнений или неравенств получается некоторая совокупность других систем, к которым приводится данная система. В таких случаях множество решений исходной системы является объединением множеств решений каждой системы, входящей в эту совокупность. Разберем один пример.

Пример 7. Решить систему неравенств

.

Решение. Раскрывая модуль в первом неравенстве системы, получим два случая: 1) при и 2) при x – 6

1) или 2)

Найдем пересечение первого и второго множества:

Используя распределительный закон пересечения относительно объединения (см. §4), будем иметь

Множество решений исходной системы является объединением множеств (9,12] и [4,5), то есть [4,5)  (9,12].

1.6. Множества точек на плоскости, задаваемые уравнениями
и неравенствами с двумя переменными

Множества точек на плоскости можно задавать их характеристическими свойствами. В разд. 1.2 мы уже познакомились с такими примерами. Кроме такого способа задания их часто задают соотношениями между координатами точек в виде уравнений или неравенств.

Аналогично неравенство y > ax 2 + bx + c задает множество точек, лежащих по одну сторону от параболы (рис. 25 и 26), а неравенство y ax 2 + bx + c задает множество точек, лежащих по другую сторону (рис. 27 и 28).

Когда имеется система уравнений или неравенств с двумя переменными, то множество решений такой системы представляет собой пересечение множеств решений каждого уравнения или неравенства, входящего в систему.

Пример. Построить множество точек, удовлетворяющих следующим соотношениям:

б) .

Решение. В случае а) соотношения равносильны следующей системе

.

Рис. 29 Рис. 30 Рис. 31

Рис. 32 Рис. 33 Рис. 34

1.7. Отображение множеств. Взаимно-однозначное
соответствие между множествами. Понятие числовой функции

1. Рассмотрим два множества А и В. Если каждому элементу а множества А некоторым способом поставлен в соответствие один элемент b множества В, то говорят, что задано отображение множества А в множество В. Записывают это так: f:A  B или b=f(a). Через f обозначают то отображение (правило), по которому это соответствие устанавливается. С помощью диаграмм Венна это изображается так:

Если же каждый элемент множества В соответствует какому-либо элементу множества А,
то говорят, что множество А отображается на множество В (рис. 36).

В примере 1 так будет, если все стулья окажутся занятыми (то есть количество учеников и количество стульев одинаковое).

Между множествами А и В установлено взаимно-однозначное соответствие (взаимно-однозначное отображение), если каждому элементу а из А поставлен в соответствие один элемент b из B, и при этом соответствии каждый элемент b из В соответствует одному и только одному элементу а из А. С помощью диаграмм взаимно-однозначное соответствие изображено на рис. 36.

В примере 2 отображение f:A  С никогда не будет взаимно-однозначным, так как, вообще говоря, количество учеников в классе всегда меньше количества букв и, кроме того, ни одна фамилия не начинается с буквы “й” или “ь”.

Приведем теперь примеры взаимно-однозначного соответствия бесконеч­ных множеств. Одним, наиболее хорошо всем знакомым, является взаимно-однозначное соответствие между множеством всех действительных чисел R и множеством точек на прямой (числовая прямая). Разберем и другой пример. Выберем на плоскости систему координат и поставим в соответствие каждой окружности вписанный в нее квадрат, стороны которого параллельны осям координат. Мы получим взаимно-однозначное соответствие между множеством всех окружностей и множеством всех квадратов, стороны которых параллельны осям координат. Другое взаимно-однозначное соответствие между этими множествами получается, если сопоставить каждой окружности описанный вокруг нее квадрат, стороны которого параллельны осям координат.

Далее рассмотрим множество А всех точек на плоскости и множество В всех окружностей на этой плоскости, имеющие заданный радиус R. Если поставить в соответствие каждой точке а окружность радиуса R с центром в этой точке, то получим взаимно-однозначное соответствие между множествами А и В.

Функцию можно задавать разными способами. Одним из способов является табличный. Например, таблица

.

1.8. Эквивалентные множества. Счетные и несчетные множества. Мощность множества.

1. Два множества называют эквивалентными, если между ними можно установить взаимно-однозначное соответствие. Проще всего проверить эквивалентность конечных множеств. Для двух конечных множеств взаимно-однозначное соответствие можно установить лишь в случае, когда они имеют одинаковое количество элементов. Поэтому конечные множества эквивалентны тогда и только тогда, когда они имеют поровну элементов. Для бесконечных множеств не имеет смысла говорить о числе элементов. Однако и среди бесконечных множеств можно найти эквивалентные.

2. Рассмотрим множество всех натуральных чисел N=<1,2,3,4. >. Любое бесконечное подмножество А множества N эквивалентно самому множеству N. В самом деле, элементы этого подмножества можно расположить в порядке возрастания и каждому поставить в соответствие его порядковый номер (перенумеровать). Получим Так как элементов в подмножестве А бесконечно много, этот процесс можно неограниченно продолжать. Тем самым устанавливается взаимно-однозначное соответствие между А и N. Нетрудно догадаться, что множество А представляет собой числовую последовательность. Таким образом, все числовые последователь­ности, содержащие различные элементы, эквивалентны множеству натуральных чисел N.

Рассмотрим теперь множество Z всех целых чисел:

Бесконечные множества, эквивалентные множеству натуральных чисел, называются счетными множествами. Иными словами, если элементы бесконечного множества можно перенумеровать, то такое множество называется счетным. Самым простым примером счетного множества является само множество N натуральных чисел. Более сложные примеры счетных множеств мы рассмотрели выше.

Теперь сформулируем основные теоремы о счетных множествах.

Теорема 1. Каждое бесконечное подмножество А счетного множества В счетно.

Теорема 2. Объединение конечного или счетного множества счетных множеств счетно.

Доказывать эти теоремы мы не будем, хотя отметим, что доказательство теоремы 1 почти ничем не отличается от приведенного выше рассуждения, когда доказывалась эквивалентность между множеством N и его подмножест­вом А.

3. До сих пор мы рассматривали лишь такие бесконечные множества, которые являются счетными. Однако не все бесконечные множества счетные, существуют и такие, элементы которых нельзя перенумеровать. Простейшим примером такого множества является множество всех точек конечного интервала, например, интервала (0,1). Ясно, что в этом множестве содержится счетное подмножество. В качестве такого подмножества можно указать, например, числовую последовательность . Но оказывается, что точек в интервале (0,1) “намного” больше, чем точек этой последователь­ности. Точнее говоря, множество точек интервала (0,1) несчетно, то есть нельзя установить взаимно-однозначного соответствия между множеством точек интервала (0,1) и множеством натуральных чисел N. Доказательство этого утверждения мы проводить не будем. Легко сообразить, что любой другой интервал длины 1 на числовой прямой эквивалентен интервалу (0,1). Вообще, произвольный интервал (a,b) конечной длины эквивалентен интервалу (0,1). Взаимно-однозначное соответствие между ними можно установить так, как показано на рис. 38.

Точно так же любой отрезок (замкнутый интервал) эквивалентен отрезку [0,1] (рис. 39).

Это утверждение означает, что квадрат содержит “столько же” точек, что и отрезок, хотя на первый взгляд кажется, что в нем должно быть “гораздо больше” точек. Доказательство этой теоремы мы приводить не будем. Кстати сказать, множества точек плоскости и пространства тоже имеют мощность континуума.

Источник