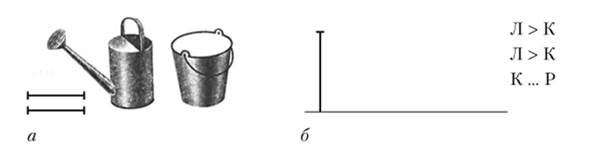Что такое дочисловой период
Задачи изучения темы.
Методика обучения математике в дочисловой период.
На уроках дочислового периода надо систематизировать и пополнять знания, умения и навыки, которыми обладают дети, дать те знания, которые необходимы для изучения нумерации.
Задачи изучения темы.
На уроках дочислового периода дети считают хором, по цепочке, индивидуально, по представлению (Сколько этажей в школе? Сколько героев в сказке «Репка»?)
— не пропускать при счете ни один предмет;
— ни один предмет не считать дважды.
2. На основе многочисленных практических упражнений дети должны научиться сравнивать две группы предметов, выясняя, в которой из них содержится больше (меньше) предметов, или же убедиться в том, что они содержат равное число предметов.
3. На этих уроках уточняются пространственные представления: дети должны научиться различать, например, на странице учебника верхнюю и нижнюю картинку, левую и правую страницы учебника, большой рисунок и маленький, научиться понимать выражения «выше», «ниже», «направо», «справа налево» и т.п.
4. Дети должны научиться понимать выражения, отражающие порядковые отношения: «следовать за», «стоять (идти) перед», «находиться между».
Продолжительность дочислового периода— приблизительно неделя (5-6 уроков). На первой неделе занятий дети учатся работать со счетным материалом, с книгой и в тетради. Формирование соответствующих умений и навыков на уроках дочислового периода только начинается, оно будет продолжено на уроках по теме «Нумерация».
В РОЗ дочисловой период не имеет четких границ. Уже на первых уроках появляются задания, направленные на развитие: сколько яблок в корзине – зад.5 (варианты ответов).
Вопрос 2. Методика изучения нумерации чисел первого десятка
· положите 3 квадрата;
· придвиньте еще один;
· Сколько всего стало квадратов?
· Как получили 4 квадрата?
· Как это записать? (3+1=4)
Проведя такие рассуждения 3-4 раза. Только с другими предметами. Выясняют, что число 4 больше числа 3 на 1. а число 3 меньше числа 4 на 1. Таким образом, число 4 стоит в ряду чисел после 3. Получая следующее число. Учащиеся знакомятся с соответствующей цифрой и учатся е писать. Такое одновременное введение числа и цифры затрудняет осознание различий между этими понятиями.
Число 0 появляется как численность множества, из которого последовательно убираются все элементы.
В системе РОЗ знакомство с числами построено иначе – число выступает как количественная характеристика множества. Порядок знакомства с однозначными числами не имеет значения. Учащиеся используют карточки с цифрами при счете предметов, сравнении множеств. Основой сравнения является установление взаимно однозначных соответствий между элементами двух множеств. Результаты сравнения фиксируются равенствами 5=5 или неравенствами 5
Дата добавления: 2016-05-11 ; просмотров: 18243 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Презентация на тему: «Дочисловой период обучения математике в начальной школе»
«Управление общеобразовательной организацией:
новые тенденции и современные технологии»
Свидетельство и скидка на обучение каждому участнику
Описание презентации по отдельным слайдам:
Презентация на тему: «Дочисловой период обучения математике» Подготовила: студентка ПНК-22 Баранова А.С.
Дочисловой период обучения математике — особая ступень в освоении математических знаний, это время адаптации ребенка к школе: от деятельности, носящей относительно свободный характер (игры), ребенок переходит к деятельности обязательной. Успешность адаптации зависит не только от его психологической готовности к учебной деятельности, но и от устойчивого желания учиться.
Система заданий дочислового периода Позволит: превратить обучение в увлекательную игру; расширить речевые возможности посредством введения в активный словарь математических терминов; совершенствовать развитие глазомера у ребенка; развить мелкую моторику пальцев рук; стимулировать развитие операций мышления; обеспечить прохождение заданий с учетом индивидуальных особенностей ребенка; повысить самостоятельность при выполнении заданий.
Понятия «больше- меньше – столько же»
Определение расположения предметов на плоскости листа
Вывод: Таким образом, в дочисловой период в поле зрения учителя должно в комплексе находиться несколько важных направлений работы, связанных с систематизацией и обобщением знаний учащихся, которые необходимы для перехода к изучению чисел.
Спасибо за внимание
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Ищем педагогов в команду «Инфоурок»
Номер материала: ДБ-897000
Не нашли то, что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
В Минпросвещения рассказали о формате обучения школьников после праздников
Время чтения: 1 минута
Число участников РДШ за 2021 год выросло в три раза
Время чтения: 2 минуты
Во всех педвузах страны появятся технопарки
Время чтения: 1 минута
Время чтения: 1 минута
Учительница из Киргизии победила в конкурсе Минпросвещения РФ «Учитель-международник»
Время чтения: 2 минуты
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Презентация по математике на тему «Дочисловой период»
«Управление общеобразовательной организацией:
новые тенденции и современные технологии»
Свидетельство и скидка на обучение каждому участнику
Описание презентации по отдельным слайдам:
Описание слайда:
Подготовила:
Тиханова Юлия Сергеевна
Дочисловой период изучения математики
Описание слайда:
Урок 1 Сравниваем
Чем похожи? Чем отличаются?
Описание слайда:
Урок 1 Сравниваем
Чем похожи? Чем отличаются?
Описание слайда:
Урок 1 Сравниваем
Чем похожи? Чем отличаются?
Описание слайда:
Урок 1 Сравниваем
Найди 9 отличий
Описание слайда:
Урок 1 Сравниваем
Смотри и выкладывай фишки:
зайцы –
медведи –
Описание слайда:
Урок 1 Сравниваем
Сколько зайцев?
Сколько синих фишек?
Сколько зверей?
Сколько фишек?
Описание слайда:
Урок 1 Сравниваем
На какие группы можно распределить предметы?
Описание слайда:
Назови каждый инструмент.
Урок 1 Сравниваем
Описание слайда:
Выложи столько фишек, сколько продуктов.
Описание слайда:
Назови принадлежности, которые ты сегодня взял с собой в школу?
Описание слайда:
Урок 2 Сравниваем
Составь предложение со словами выше, ниже, толще, тоньше, длиннее и короче.
Серый дом выше красного.
Красный дом ниже серого.
Описание слайда:
Описание слайда:
Урок 2 Сравниваем
Назови фигуру.
Сравни фигуры. Используй слова форма, цвет, размер.
Описание слайда:
Урок 2 Сравниваем
Раздели фигуры на три группы;
на две группы.
Описание слайда:
Урок 2 Сравниваем
Смотри и выкладывай фишки. Сколько карандашей?
Описание слайда:
Урок 2 Сравниваем
Слушай и выкладывай фишки?
Сколько?
В грузовике 3 мешка картошки.
У Андрея 4 апельсина.
В клетке 5 хомяков.
У Маши 2 собаки.
Описание слайда:
Автобус едет справа налево. В каком направлении едут другие машины?
Урок 3 Называем по порядку.
Слева направо. Справа налево
Описание слайда:
Урок 3 Называем по порядку.
Слева направо. Справа налево
Назови цвета квадратов по порядку слева направо.
Назови цвет каждого квадрата, начиная с самого большого.
Описание слайда:
Урок 3 Называем по порядку.
Слева направо. Справа налево
В каком порядке колобок встретил остальных героев? Назови правильный порядок.
Сколько героев
было в сказке?
Описание слайда:
Описание слайда:
Урок 4 Знакомимся с таблицей
В Расположи фигуры в большой таблице так:
Где находится каждая из фигур? Используй слова строка, столбец, слева вверху, справа внизу.
Описание слайда:
Урок 4 Знакомимся с таблицей
Смотри и выкладывай фишки. Сколько фишек? Сколько бабочек?
Описание слайда:
Урок 4 Знакомимся с таблицей
Слушай и выкладывай фишки. Сколько?
В наборе: три желтых чашки и две синие.
У Андрея игрушки: две машинки и один солдатик.
А у Маши: кукла, медведь и самолёт.
Описание слайда:
Урок 4 Знакомимся с таблицей
Кто идёт в садит перед котов?
Кто идёт первым?
третьим?
последним?
Описание слайда:
Урок 4 Знакомимся с таблицей
Кто идёт между хомяки и котами? Между медведями и утками?
Кто-нибудь идёт между поросятами и медведями?
Описание слайда:
Внутри или вне обруча девочка в красном сарафане?
Где девочка в розовой кофте?
Описание слайда:
Покажи и назови каждую фигуру внутри «кольца», вне кольца.
Описание слайда:
Какие машины едут справа налево? Сколько их?
Выложи столько же красных фишек.
Сколько машин едут слева направо? Вложи фишки.
Описание слайда:
Выложи столько фишек, сколько свечей, конфет и яблок.
Описание слайда:
Замени каждую конфету фишкой.
Сколько конфет может быть у Маши? Сколько у Димы?
Описание слайда:
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Ищем педагогов в команду «Инфоурок»
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
также Вы можете выбрать тип материала:
Общая информация
Похожие материалы
Презентация по математике на тем «Знакомство с геометрией»
Тренажер по алгебре по теме «Теорема Виета»
Презентация на тему :»Геометрические фигуры»
Презентация к уроку математики
Статья Выявление индивидуальных особенностей учащихся и использование их для повышения мотивации при обучении математике»»
Мастер – класс по созданию и использованию Платформы Google Forms.
Исследовательская работа учащегося по теме » Что наша жизнь? Игра!»
Презентация к уроку «Степень числа», 5 класс
Не нашли то что искали?
Воспользуйтесь поиском по нашей базе из
5438195 материалов.
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Во всех педвузах страны появятся технопарки
Время чтения: 1 минута
ОНФ планирует решить проблему с низкими зарплатами водителей школьных автобусов в России
Время чтения: 1 минута
Число участников РДШ за 2021 год выросло в три раза
Время чтения: 2 минуты
В Минпросвещения рассказали о формате обучения школьников после праздников
Время чтения: 1 минута
В Липецкой области начинающие педагоги получат 120 тысяч рублей
Время чтения: 0 минут
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Методика работы в дочисловой период
Подготовительный (дочисловой) период обучения математике — особая ступень в освоении математических знаний, это время адаптации ребенка к школе: от деятельности, носящей относительно свободный характер (игры), ребенок переходит к деятельности обязательной. Успешность адаптации зависит не только от его психологической готовности к учебной деятельности (наличие необходимого запаса представлений и понятий, определенного уровня развития мышления и речи), но и от устойчивого желания учиться. Важнейшее значение для ребенка, ставшего школьником, имеет мотивация учения. На первых порах основу мотивации составляет интерес к школе вообще, но ее основу должен составлять интерес к учению. В то же время деятельность учения для ребенка не является в сущности новой (обучение в детском саду зачастую предваряет знакомство ребенка с такой деятельностью почти в тех же формах, что и в школе) интерес к учению должен поддерживаться учителем, прежде всего как интерес к приобретению новых знаний. При этом особое значение приобретает не столько содержание учебного материала, сколько сам процесс учебной работы школьника, способы и формы осуществления познавательной деятельности, направляемой учителем.
Содержание обучения на этом этапе во многом совпадает с тем, с чем дети познакомились в детском саду. Как правило, сюда включаются темы: сравнение и счет предметов; множества и действия над ними, пространственные и временные отношения.
Задания на сравнение предметов по выделяемым свойствам направлены в основном на выявление знаний и умений ребенка, приобретенных в дошкольном образовании. Предметы сравниваются по форме, по цвету, по размеру. В процессе сравнения у школьников формируются умения оперировать наглядно представленными отношениями. Привычные явления, протекающие во времени, сравниваются по их следованию: раньше, позже, сначала, потом. Количественный и порядковый счет предметов посредством количественных или порядковых числительных, последовательность которых до десяти предполагается детям известной, производится путем действий с самими предметами, или с их изображениями в контексте некоторой ситуации. Сравнение групп предметов но количеству производится путем установления соответствующих пар по одному из каждой группы в паре, приводит к выявлению отношения «на сколько больше», «на сколько меньше». При этом задания формулируются так, что пересчет предметов сравниваемых групп не предполагается. Учитель должен отчетливо понимать, сравниваются не числа, их сравнение — иная задача более высокого уровня абстракции, а сравниваются множества конкретных предметов. Организация самостоятельной познавательной деятельности ребенка своими руками с помощью листа рабочей тетради представлена на рис. 6.1.
Ознакомление школьников с понятием «множество» осуществляется в дочисловом периоде или в неявной форме, как, например, в УМК «Школа России», или в явной форме, как в УМК «Перспектива».
В явном виде множество характеризуется как любая группа в чем-то сходных предметов. Каждый предмет группы — элемент множества. По общему для всех элементов признаку множество получает название: множество конфет, множество птиц и т.п. Части множества также выделяются по некоторому общему признаку. Признак может указываться, а может придумываться самими детьми. Например, во множестве фигур (рис. 6.2), части выделяются по признакам, которые придумывают сами учащиеся.
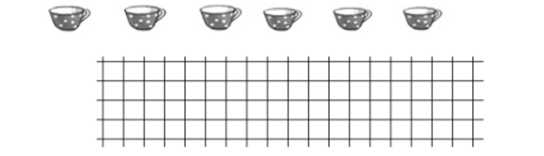
Нарисуй в клеточках столько же квадратов, сколько чашек
Чего больше, кругов или звездочек? На сколько больше? На сколько меньше?
Рис. 6.1. Пример листа рабочей тетради
Рис. 6.2. Выделение подмножеств данного множества
Понятие равенства множеств (равные множества состоят из одних и тех же элементов) позволяет ввести знаки «=», «=?». Установление неравенства множеств, содержащих одно и то же количество элементов, предупреждает распространенную ошибку: множества равны, если они содержат одно и то же количество элементов. Например, задание «поставь знаки = или *» (рис. 6.3) позволяет уточнить представления детей о множестве и экстраполировать эти представления па понятие «численность множества».
Рис. 6.3. Понятие «равенство множеств»
Умение свободно ориентироваться в двумерном пространстве (в пространстве листа бумаги, доски, поверхности стола и т.н.) и одномерном (на линии) составляет одно из необходимых метапредметных умений, формируемых на этом этапе обучения. Освоение «предметных значений» — пространственных отношений невозможно только в вербальном плане, необходима организация деятельности детей но оперированию такими отношениями (В. П. Зинченко). Например, выполняя задание «Нарисуй дорожку зайцу, если ему надо пройти к ежику так, чтобы каждая березка была справа от него, а каждая елочка — слева» (рис. 6.4) на листе рабочей тетради, учащиеся овладевают относительностью понятий «слева», «справа», самостоятельно оперируя данными понятиями в процессе решения поставленной задачи.
Рис. 6.4. Ориентация в пространстве «от себя»
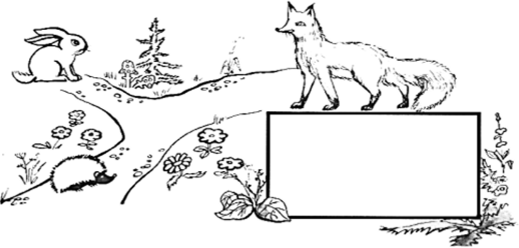
Формирование представлений о точке как обозначении местоположения предмета и о линии как обозначении траектории движения начинается в дочисловом периоде. С другой стороны, учащиеся овладевают умением абстрагироваться от несущественных в данной ситуации свойств объектов и обозначить то, что существенно. Например, решая задачу «Нарисуй в рамке дорожки, по которым бегут звери, и отметь на них точки, где находятся лиса, заяц и еж» (рис. 6.5), дети отвлекаются от ширины дорожек и от размеров зверей, выделяя только их местоположение.
Рис. 6.5. Точка как местоположении предмета
Таким образом, в содержательном плане данный этап обучения подготавливает учащихся к восприятию понятий «число — мощность конечного множества» и «число — характеристика места в последовательности», а также к восприятию геометрической фигуры как идеализированного представления формы.
В системе Д. Б. Эльконина — В. В. Давыдова (авторы В. В. Давыдов, С. Ф. Горбов и другие) дочисловой период обучения построен на иных основаниях, его цель подготовка к введению понятия «число — мера величины», вследствие чего формирование представлений о величинах и способах их сравнения образует основное содержание подготовительного периода обучения. Если первоначально площади, длины, объемы, массы сравниваются способом наложения, а результат сравнения фиксируется словами «одинаковые», «неодинаковые», то в дальнейшем результат сравнения обозначается отрезками так, что большая величина обозначается большим отрезком.
Обозначение величин буквами, никак наглядно не отражающими результат сравнения, фиксирует его специальными знаками-символами. Учащимися решаются задачи вида: узнай, но какому признаку сравнивались предметы (рис. 6.6, а); дорисуй и допиши обозначенные буквами величины, где К — величина, обозначенная вертикальным отрезком, величины Л и Р дорисуй также отрезками, соблюдая отношения между ними, заданные неравенствами. Поставь пропущенный знак неравенства (рис. 6.6, 6).
Рис. 6.6. Кодирование математической информации различными знаковыми
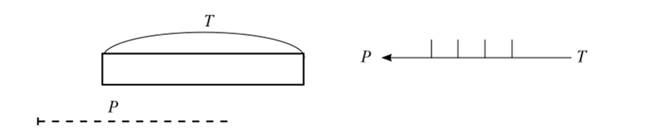
Необходимость сравнения величин в условиях, когда наложение невозможно, стимулирует учащихся на поиск решения возникшей проблемы. Использование величины-посредника, а затем посредника, с которым могут сравниваться любые величины данного рода, называемого меркой, открывает путь к решению проблемы сравнения во всех возможных ситуациях введением меток, фиксирующих действия, производимые в процессе сравнения. Если известны метки и мерка, то по этим данным можно воспроизвести величину. Например, по мерке Т и меткам 11 | | строится величина Р (рис. 6.7). Метки как способ записи результата сравнения являются ступенью, ведущей к предметному осмыслению понятия «число — мера величины».
Рис. 6.7. Конструирование величины по заданному эталону и меткам
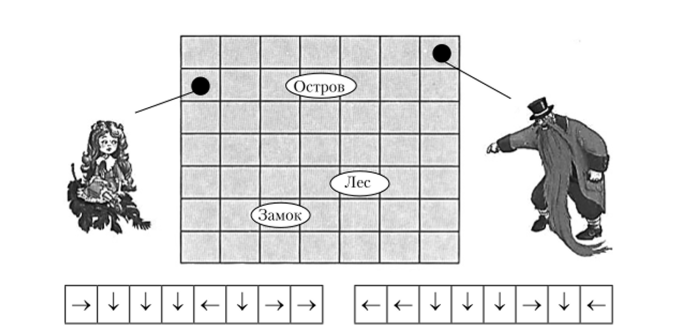
Как нетрудно заметить, уже на этом этапе освоения математики школьники знакомятся с различными средствами представления математической информации: словами повседневного языка, знаками-иконами, знаками- индексами, знаками-символами. Например, в УМК «Перспектива» (авторы В. Г. Дорофеев, Т. Н. Миракова) у учащихся специально формируется умение кодировать и раскодировать информацию, представляемую знаками- индексами. В задании (рис. 6.8) требуется восстановить путь героев, если стрелки слева показывают путь Мальвины, а справа — Карабаса-Барабаса (герои начинают движение из указанных точек).
Рис. 6.8. Действие по заданному алгоритму
Методы и средства обучения в столь ответственный период жизни первоклассника должны быть привлекательными для него и тем, что увеличивают долю его самостоятельности в сравнении с детским садом. Выполняя задания на листе рабочей тетради, где приходится рассуждать, рисовать, раскрашивать для выполнения поставленной задачи при ненавязчивой и благожелательной помощи учителя, ребенок может чувствовать себя не только вполне успешным, но и защищенным. Такому положению его на уроке способствует и смена видов деятельности, в частности, на работу с предметными моделями математических объектов. Например, из палочек и пластилиновых шариков изготавливаются каркасные модели куба, пирамиды. Другими словами, до- числовой период обучения математике требует от учителя максимальной отдачи во всех формах педагогического взаимодействия с детьми, в первую очередь в организации познавательной деятельности учащихся.