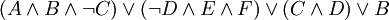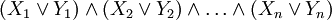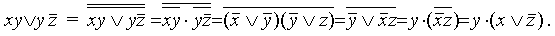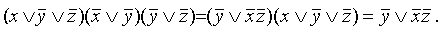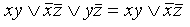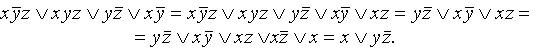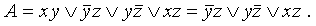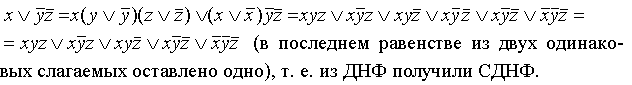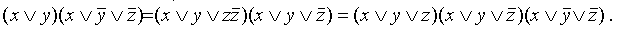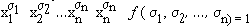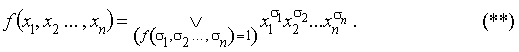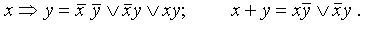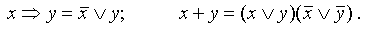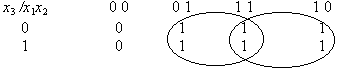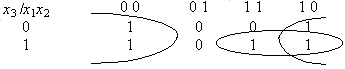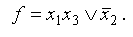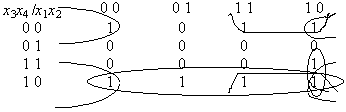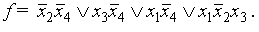Что такое днф в логике
Дизъюнктивная нормальная форма
Дизъюнкти́вная норма́льная фо́рма (ДНФ) в булевой логике — нормальная форма, в которой булева формула имеет вид дизъюнкции конъюнкций литералов. Любая булева формула может быть приведена к ДНФ. [1] Для этого можно использовать закон двойного отрицания, закон де Моргана, закон дистрибутивности. Дизъюнктивная нормальная форма удобна для автоматического доказательства теорем.
Содержание
Примеры и контрпримеры



Построение ДНФ
Алгоритм построения ДНФ
1) Избавиться от всех логических операций, содержащихся в формуле, заменив их основными: конъюнкцией, дизъюнкцией, отрицанием. Это можно сделать, используя равносильные формулы:

2) Заменить знак отрицания, относящийся ко всему выражению, знаками отрицания, относящимися к отдельным переменным высказываниям на основании формул:

3) Избавиться от знаков двойного отрицания.
4) Применить, если нужно, к операциям конъюнкции и дизъюнкции свойства дистрибутивности и формулы поглощения.
Пример построения ДНФ
Приведем к ДНФ формулу :
Выразим логические операции → и ↓ через :
В полученной формуле перенесем отрицание к переменным и сократим двойные отрицания:
Используя закон дистрибутивности, приводим формулу к ДНФ:
k-дизъюнктивная нормальная форма
k-дизъюнктивная нормальной формой называют дизъюнктивную нормальную форму, в которой каждая конъюнкция содержит ровно k литералов.
Например, следующая формула записана в 2-ДНФ:
Переход от ДНФ к СДНФ
Если в какой-то простой конъюнкции недостает переменной, например, Z, вставляем в нее выражение :


Таким образом, из ДНФ получили СДНФ.
Формальная грамматика, описывающая ДНФ
Следующая формальная грамматика описывает все формулы, приведенные к ДНФ:
где обозначает произвольную булеву переменную.
См. также
Примечания
Литература
Ссылки
Полезное
Смотреть что такое «Дизъюнктивная нормальная форма» в других словарях:
дизъюнктивная нормальная форма — ДНФ — [http://www.rfcmd.ru/glossword/1.8/index.php?a=index d=23] Тематики защита информации Синонимы ДНФ EN disjunctive normal formDNF … Справочник технического переводчика
дизъюнктивная нормальная форма — norminė disjunkcinė forma statusas T sritis automatika atitikmenys: angl. disjunctive normal form; DNF vok. disjungtive Normalform, f rus. дизъюнктивная нормальная форма, f pranc. forme disjonctive normale, f … Automatikos terminų žodynas
ТУПИКОВАЯ ДИЗЪЮНКТИВНАЯ НОРМАЛЬНАЯ ФОРМА — представляющая заданную булеву функцию дизъюнктивная нормальная форма (д. н. ф.), к рую нельзя упростить ни вычеркиванием буквы из нек рой конъюнкции, ни удалением какой либо конъюнкции. Минимальная д. н. ф. получается из сокращенной д. н. ф.… … Математическая энциклопедия
Нормальная форма (математика) — У этого термина существуют и другие значения, см. Нормальная форма (значения). Нормальная форма в математике простейший либо канонический вид, к которому объект приводится эквивалентными преобразованиями[1]. Содержание 1 Жорданова… … Википедия
Нормальная форма (значения) — Нормальная форма: Нормальная форма в базах данных свойство отношения в реляционной модели данных. Нормальная форма в математике в каком либо смысле простейший либо канонический вид, к которому объект приводится преобразованиями,… … Википедия
Конъюнктивная нормальная форма — (КНФ) в булевой логике нормальная форма, в которой булева формула имеет вид конъюнкции дизъюнкций литералов. Конъюнктивная нормальная форма удобна для автоматического доказательства теорем. Любая булева формула может быть приведена к… … Википедия
СОКРАЩЕННАЯ НОРМАЛЬНАЯ ФОРМА — булевой функции дизъюнктивная нормальная форма (д. н. ф.), представляющая собой дизъюнкцию всех простых импликант данной функции. Конъюнкция наз. импликантой булевой функции f, если справедливо соотношение Импликанта наз. простой, если после… … Математическая энциклопедия
СОВЕРШЕННАЯ НОРМАЛЬНАЯ ФОРМА — совершенная дизъюнктивная или совершенная конъюнктивная нормальная форма (см. Булевых функций нормальные формы) … Математическая энциклопедия
Что такое днф в логике
Дизъюнкти́вная норма́льная фо́рма (ДНФ) в булевой логике — нормальная форма, в которой булева формула имеет вид дизъюнкции нескольких конъюнктов.
Например, следующие формулы записаны в ДНФ:
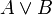
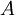
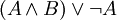
Дизъюнктивная нормальная форма удобна для автоматического доказывания теорем.
Приведение булевой формулы к ДНФ
Любая булева формула может быть приведена к ДНФ. Впрочем, при этом размер булевой формулы может возрасти экспоненциально. Так, например, 2 n конъюнктов потребуется, чтобы записать следующую формулу:
Формальная грамматика, описывающая ДНФ
Следующая формальная грамматика описывает все формулы, приведенные к ДНФ:
где обозначает произвольную булеву переменную.
См. также
Полезное
Смотреть что такое «ДНФ» в других словарях:
ДНФ — динитрофенол Словарь: С. Фадеев. Словарь сокращений современного русского языка. С. Пб.: Политехника, 1997. 527 с. ДНФ дизъюнктивная нормальная форма матем. ДНФ динатрийфосфат Источник: http://www.him.ru/ … Словарь сокращений и аббревиатур
ДНФ — динитрофенол … Словарь сокращений русского языка
АЛГЕБРА ЛОГИКИ — система алгебраич. методов решения логич. задач, а также совокупность задач, решаемых такими методами. А. л. в узком смысле слова алгебраич. (табличное, матричное) построение классич. логики высказываний, в котором рассматриваются… … Философская энциклопедия
Алгебра логики — раздел математической логики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности), и логические операции над ними. А. л. возникла в середине 19 в. в трудах Дж. Буля (См. Буль) и развивалась… … Большая советская энциклопедия
Дизъюнктивная нормальная форма — (ДНФ) в булевой логике нормальная форма, в которой булева формула имеет вид дизъюнкции конъюнкций литералов. Любая булева формула может быть приведена к ДНФ.[1] Для этого можно использовать закон двойного отрицания, закон де Моргана, закон… … Википедия
Булева функция — В данной статье или разделе имеется список источников или внешних ссылок, но источники отдельных утверждений остаются неясными из за отсутствия сносок … Википедия
Карта Карно — Рис. 1 Пример Куба Карно Куб Карно графический способ минимизации переключательных (булевых) функций, обеспечивающий относительную простоту работы с большими выражениями и устранение потенциальных гонок. Представляет собой операции попарного… … Википедия
СДНФ — (Совершенная Дизъюнктивная Нормальная Форма) это такая ДНФ, которая удовлетворяет трём условиям: в ней нет одинаковых элементарных конъюнкций в каждой конъюнкции нет одинаковых пропозициональных букв каждая элементарная конъюнкция содержит… … Википедия
ДНФ, СДНФ, КНФ, СКНФ
Простой конъюнкцией называется конъюнкция одной или нескольких переменных, при этом каждая переменная встречается не более одного раза (либо сама, либо ее отрицание).
Например, 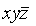
Дизъюнктивной нормальной формой (ДНФ) называется дизъюнкция простых конъюнкций.
Например, выражение 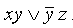
Совершенной дизъюнктивной нормальной формой (СДНФ) называется такая дизъюнктивная нормальная форма, у которой в каждую конъюнкцию входят все переменные данного списка (либо сами, либо их отрицания), причем в одном и том же порядке.
Например, выражение 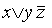
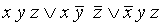
Аналогичные определения (с заменой конъюнкции на дизъюнкцию и наоборот) верны для КНФ и СКНФ. Приведем точные формулировки.
Простой дизъюнкцией называется дизъюнкция одной или нескольких переменных, при этом каждая переменная входит не более одного раза (либо сама, либо ее отрицание).Например, выражение 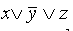
Конъюнктивной нормальной формой (КНФ) называется конъюнкция простых дизъюнкций (например выражение 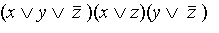
Совершенной конъюнктивной нормальной формой (СКНФ) называется такая КНФ, у которой в каждую простую дизъюнкцию входят все переменные данного списка (либо сами, либо их отрицания), причем в одинаковом порядке.
Например, выражение 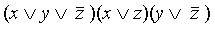
Приведем алгоритмы переходов от одной формы к другой. Естественно, что в конкретных случаях (при определенном творческом подходе) применение алгоритмов бывает более трудоемким, чем простые преобразования, использующие конкретный вид данной формы:
а) переход от ДНФ к КНФ
Алгоритм этого перехода следующий: ставим над ДНФ два отрицания и с помощью правил де Моргана (не трогая верхнее отрицание) приводим отрицание ДНФ снова к ДНФ. При этом приходится раскрывать скобки с использованием правила поглощения (или правила Блейка). Отрицание (верхнее) полученной ДНФ (снова по правилу де Моргана) сразу дает нам КНФ:
Заметим, что КНФ можно получить и из первоначального выражения, если вынести у за скобки;
б) переход от КНФ к ДНФ
Этот переход осуществляется простым раскрытием скобок (при этом опять-таки используется правило поглощения)
Таким образом, получили ДНФ.
Обратный переход (от СДНФ к ДНФ) связан с проблемой минимизации ДНФ. Подробнее об этом будет рассказано в разд. 5, здесь же мы покажем, как упростить ДНФ (или СДНФ) по правилу Блейка. Такая ДНФ называется сокращенной ДНФ;
в) сокращение ДНФ (или СДНФ) по правилу Блейка
Применение этого правила состоит из двух частей:
— если среди дизъюнктных слагаемых в ДНФ имеются слагаемые 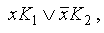
— если добавляемое слагаемое уже содержалось в ДНФ, то его можно отбросить совсем, например,
Разумеется, сокращенная ДНФ не определяется единственным образом, но все они содержат одинаковое число букв (например, имеется ДНФ 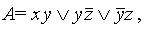
в) переход от ДНФ к СДНФ
Если в какой-то простой конъюнкции недостает переменной, например, z, вставляем в нее выражение 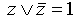
г) переход от КНФ к СКНФ
Этот переход осуществляется способом, аналогичным предыдущему: если в простой дизъюнкции не хватает какой-то переменной (например, z, то добавляем в нее выражение 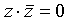
Таким образом, из КНФ получена СКНФ.
Заметим, что минимальную или сокращенную КНФ обычно получают из соответствующей ДНФ.
4. Представление логических функций
в виде СДНФ (СКНФ)
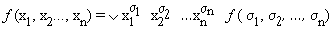
а) Пусть f(x1, x2, …, xn)= 1. Тогда слева в формуле (* ) стоит 1. Докажем, что и справа в этом случае стоит 1, для чего достаточно указать одно дизъюнктное слагаемое, равное 1. Но среди всех наборов (s1, s2, …, sп) имеется набор s1 = х1, s2 = х2, …, sп = хп. Очевидно, что для этого набора слагаемое 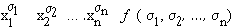
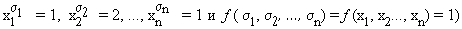
б) Пусть f(x1, x2, …, xn) = 0. Предположим, что справа стоит не ноль, а единица, тогда какое-то слагаемое тоже должно равняться 1, т. е. для некоторого набора
Доказательство. Пусть f(x1,x2,…,xn) не равна тождественному нулю, тогда в дизъюнкции можно не записывать слагаемые, равные нулю, а из формулы (* ) следует следующее представление для данной функции
Следствие. Любую логическую (булеву) функцию можно выразить через три логические функции: конъюнкцию, дизъюнкцию и отрицание.
Набор функций, через которые можно выразить любые другие функции, называется полным набором (более точные формулировки даны в разд. 7). Таким образом, конъюнкция, дизъюнкция и отрицание являются полным набором.
По аналогии с представлением любой функции (не равной тождественному нулю) в виде СДНФ можно функцию (не равную тождественной 1) представить в виде СКНФ: простая дизъюнкция составляется для тех наборов переменных (х1, х2, …, хп), для которых f(x1, x2,…, xn) = 0, причем если хi = 1, то в этой дизъюнкции берем 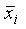
Пример. Составить для импликации и сложения по модулю 2 СДНФ и СКНФ.
Тогда СДНФ для этих функций:
СКНФ для этих функций:
5. Нахождение сокращенной ДНФ
по таблице истинности (карты Карно)
Доказано, что любую функцию (кроме тождественного нуля) можно представить в виде СДНФ. На практике часто бывает удобно получить (вместо СДНФ) как можно более “короткую” ДНФ. Словам “короткая ДНФ” можно придать разный смысл, а именно:
ДНФ называется минимальной, если она содержит наименьшее число букв (разумеется, среди всех ДНФ ей равносильных); ДНФ называется кратчайшей, если она содержит минимальное число знаков дизъюнкции Ú ; тупиковой, если уничтожение одной или нескольких букв в ней приводит к неравной ДНФ и сокращенной ДНФ, если ее упрощение проведено с помощью правила Блейка.
На практике наиболее важной представляется нахождение минимальной ДНФ, но алгоритм ее нахождения по существу является вариантом перебора всех равносильных ДНФ. Алгоритмически проще всего находить сокращенную ДНФ (эти алгоритмы были даны в разд. 3). Заметим, что если функция п переменныхзаданасвоейтаблицей истинности, топравило Блейка имеет простой геометрический смысл. Именно, если все возможные наборы переменных представить себе как вершины п-мерного куба со стороной равной 1 (всего вершин будет 2 п ) в декартовой системе координат, то надо отметить те вершины, на которых значение функции равно 1, и если какие-то из этих единиц лежат на “прямой”, “плоскости” или “гиперплоскости” в п-мерном пространстве, то в сокращенную ДНФ будут входить “уравнения” этих прямых или гиперплоскостей по известному правилу: если в это уравнение входило составной частью х = 0,то в сокращенную ДНФ входит 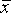
Карты Карно позволяют эти геометрические идеи использовать при п = 3, 4, 5, для функций, заданных своей таблицей истинности. При больших п картыКарнопрактическинеиспользуются. Рассмотрим отдельно (и более подробно) случаи п = 3, 4.
Составляем таблицу истинности для данной конкретной функции п = 3 в виде таблицы, приведенной в примере 5.1. (Заметим, что для х1и х2естественный порядок набора переменных здесь нарушен. Это сделано для того, чтобы при переходе от данного к следующему набору переменных в этом наборе менялась только одна цифра). Прямая содержит 2 вершины, плоскость – 4, гиперплоскости – 8, 16 и т. д. вершин, поэтому объединять можно 2 рядом стоящие единицы или 4, 8, 16 и т. д. Карты Карно соединяются “по кругу”, т. е. наборы (10) и (00) считаются рядом стоящими.
Пример 5.1. Пусть задана функция:
Видно, ее СДНФ содержит (по числу 1) 6 дизъюнктных слагаемых, но ее сокращенная ДНФ содержит (после объединения единиц) всего 2 буквы
Пример 5.2. Следующий пример показывает, “как соединять единицы по кругу”.
Здесь сокращенная ДНФ содержит 2 слагаемых (СДНФ содержала бы 5):
Пример 5.3. Пример показывает использование карт Карно при п = 4.
Здесь сокращенная ДНФ содержит 4 слагаемых (СДНФ содержит 8):
При п = 5 использование карт Карно является несколько более сложным и здесь не приводится.
Сокращённая и минимальная ДНФ
Содержание
Сокращенная ДНФ [ править ]
Функцию можно записать с помощью сокращенной ДНФ не единственным способом.
Минимальная ДНФ [ править ]
| Определение: |
| Минимальная ДНФ (англ. minimal disjunctive normal form) — такая сокращенная ДНФ, в которой содержится минимальное количество вхождений переменных. |
Каждая минимальная ДНФ является сокращенной, но не каждая сокращенная — минимальна. Например, запись [math](x \land y) \lor (y \land z) \lor (x \land z)[/math] является минимальной ДНФ для медианы (она же сокращенная, как видно в примере выше); а запись [math](x \land y \land \lnot z) \lor (\neg x \land y \land z) \lor (x \land z)[/math] — не минимальная, но сокращенная ДНФ.
Минимизация ДНФ [ править ]
Рассмотрим несколько способов минимизации дизъюнктивных нормальных форм:
Визуализация гиперкубами [ править ]
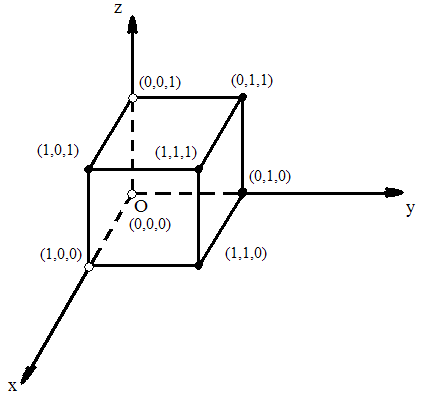
Этот способ работает при количестве переменных не больше трёх (в противном необходимо вводить четвёртое или следующие за ним измерения для представления фигур). Сначала мы рисуем куб в системе отсчёта [math]Oxyz[/math] (названия координатных осей соответствуют названиям переменных). Затем каждую вершину обрабатываем следующим образом:
пока у нас есть незакрашенные вершины, мы выбираем грань, либо вершину, либо ребро, на которых больше всего закрашенных чёрным вершин и ещё не обработанных вершин.
Карты Карно [ править ]
| [math]w[/math] | [math]w[/math] | [math]\neg | [math]\neg |
|---|---|---|---|
| [math]z[/math] | [math]\neg | [math]\neg | [math]z[/math] |
| [math]y[/math] | [math]x[/math] | ||
| [math]y[/math] | [math]\neg | ||
| [math]\neg | [math]\neg | ||
| [math]\neg | [math]x[/math] |
Теперь для каждого конъюнкта мы помечаем соответствующую ему ячейку таблицы.
[math](\neg X \wedge Y \wedge \neg Z \wedge W) \vee (\neg X \wedge Y \wedge \neg Z \wedge \neg W) \vee (\neg X \wedge \neg Y \wedge \neg Z \wedge W) \vee (\neg X \wedge \neg Y \wedge \neg Z \wedge \neg W) \vee (\neg X \wedge \neg Y \wedge Z \wedge \neg W) \vee (X \wedge \neg Y \wedge \neg Z \wedge \neg W) \vee (X \wedge \neg Y \wedge Z \wedge \neg W)[/math]
будет выглядеть на картах Карно так:
| [math]w[/math] | [math]w[/math] | [math]\neg | [math]\neg |
|---|---|---|---|
| [math]z[/math] | [math]\neg | [math]\neg | [math]z[/math] |
| [math]y[/math] | [math]x[/math] | ||
| [math]y[/math] | [math]\neg | [math]1[/math] | [math]1[/math] |
| [math]\neg | [math]\neg | [math]1[/math] | [math]1[/math] |
| [math]\neg | [math]x[/math] | [math]1[/math] | [math]1[/math] |
Теперь покрываем прямоугольниками (длины сторон которых — степени двойки ( [math]1, 2, 4[/math] )) те ячейки карт Карно, которые содержат в себе единицу (на каждом ходу мы выбираем такой прямоугольник, чтобы он покрывал наибольшее количество ещё не покрытых клеток) до тех пор, пока не покроем все такие ячейки.
Для карт Карно на примере это выглядело бы так:
| [math]w[/math] | [math]w[/math] | [math]\neg | [math]\neg | |
|---|---|---|---|---|
| [math]z[/math] | [math]\neg | [math]\neg | [math]z[/math] | |
| [math]y[/math] | [math]x[/math] | |||
| [math]y[/math] | [math]\neg | [math]1[/math] | [math]1[/math] | |
| [math]\neg | [math]\neg | [math]1[/math] | [math]1[/math] | [math]1[/math] |
| [math]\neg | [math]x[/math] | [math]1[/math] | [math]1[/math] |
После этого записываем каждый прямоугольник в виде конъюнкта, в котором будут указаны только те переменные, которые одинаковы для всех ячеек этого прямоугольника.
То есть, в этом примере получаем: [math](\neg Z \wedge \neg X) \vee (\neg W \wedge \neg Y)[/math]
Метод Квайна [ править ]
Этот метод основан на применении двух основных операций:
Метод состоит в последовательном выполнении всех возможных склеиваний и затем всех поглощений частей СДНФ пока это может быть осуществимо.
Описание алгоритма [ править ]
Алгоритм завершается, когда подмножество является пустым, либо нельзя выполнить ни одной операции неполного попарного склеивания. После выполнения этого алгоритма будет получена сокращенная (но еще не минимальная) форма.
Переход от сокращённой формы к минимальной осуществляется с помощью специальной таблицы. Члены СДНФ заданной функции вписываются в столбцы, а в строки — члены сокращённой формы. Отмечаются столбцы членов СДНФ, которые поглощаются отдельными элементами сокращённой формы.
Члены сокращённой формы, не подлежащие исключению, образуют ядро. Такие члены определяются по вышеуказанной матрице. Для каждой из них имеется хотя бы один столбец, перекрываемый только этим членом.
Для получения минимальной формы достаточно выбрать из членов сокращённой формы, не входящих в ядро, такое минимальное их число с минимальным количеством букв в каждом из этих членов, которое обеспечит перекрытие всех столбцов, не перекрытых членами ядра.
Пример [ править ]
Функция от четырёх аргументов задана следующей таблицей:
Проведём операции неполного склеивания и поглощения:
На данном шаге все элементы вида [math]Ax[/math] или [math]A \neg x[/math] участвовали в операциях попарного неполного склеивания и были поглощены своими собственными частями. Поэтому элементы сокращённой ДНФ на этом шаге не получены.
На данном этапе получаем элементы сокращённой ДНФ [math]\neg x \land \neg z \land \neg w[/math] и [math]y \land \neg z \land \neg w[/math]
| № | Элементарная конъюнкция | Поглощение |
|---|---|---|
| [math]1[/math] | [math]xz[/math] | |
| [math]2[/math] | [math]xy[/math] |
Обе элементарные конъюнкции на данном шаге являются элементами сокращённой ДНФ.
В результате выполнения алгоритма мы получаем следующую сокращённую ДНФ: [math](\neg x \land \neg z \land \neg w) \lor (y \land \neg z \land \neg w) \lor (x \land z) \lor (x \land y) [/math]
Переход от сокращённой формы к минимальной: