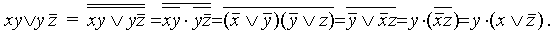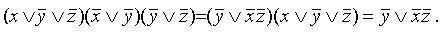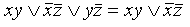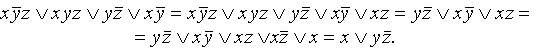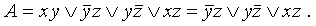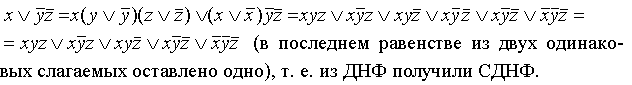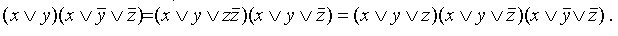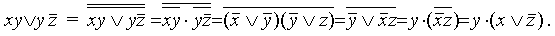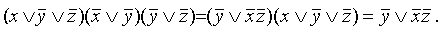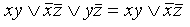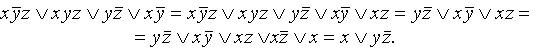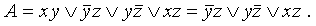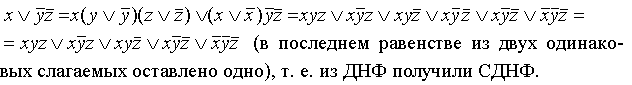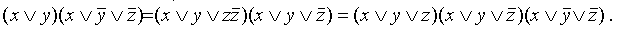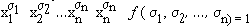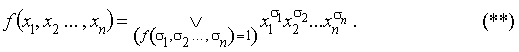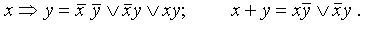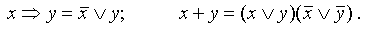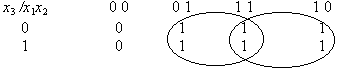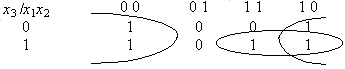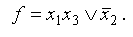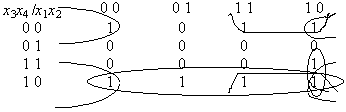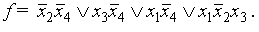Что такое днф и сднф
«Учебник по дискретной математике ДНФ, СДНФ, КНФ, СКНФ»
Например, 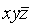
Дизъюнктивной нормальной формой (ДНФ) называется дизъюнкция простых конъюнкций.
Например, выражение 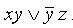
Например, выражение 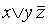
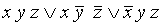
Аналогичные определения (с заменой конъюнкции на дизъюнкцию и наоборот) верны для КНФ и СКНФ. Приведем точные формулировки.
Простой дизъюнкцией называется дизъюнкция одной или нескольких переменных, при этом каждая переменная входит не более одного раза (либо сама, либо ее отрицание).Например, выражение 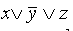
Конъюнктивной нормальной формой (КНФ) называется конъюнкция простых дизъюнкций (например выражение 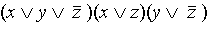
Совершенной конъюнктивной нормальной формой (СКНФ) называется такая КНФ, у которой в каждую простую дизъюнкцию входят все переменные данного списка (либо сами, либо их отрицания), причем в одинаковом порядке.
Например, выражение 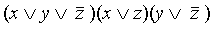
Приведем алгоритмы переходов от одной формы к другой. Естественно, что в конкретных случаях (при определенном творческом подходе) применение алгоритмов бывает более трудоемким, чем простые преобразования, использующие конкретный вид данной формы:
а) переход от ДНФ к КНФ
Алгоритм этого перехода следующий: ставим над ДНФ два отрицания и с помощью правил де Моргана (не трогая верхнее отрицание) приводим отрицание ДНФ снова к ДНФ. При этом приходится раскрывать скобки с использованием правила поглощения (или правила Блейка). Отрицание (верхнее) полученной ДНФ (снова по правилу де Моргана) сразу дает нам КНФ:
Заметим, что КНФ можно получить и из первоначального выражения, если вынести у за скобки;
б) переход от КНФ к ДНФ
Этот переход осуществляется простым раскрытием скобок (при этом опять-таки используется правило поглощения)
Таким образом, получили ДНФ.
Обратный переход (от СДНФ к ДНФ) связан с проблемой минимизации ДНФ. Подробнее об этом будет рассказано в разд. 5, здесь же мы покажем, как упростить ДНФ (или СДНФ) по правилу Блейка. Такая ДНФ называется сокращенной ДНФ;
в) сокращение ДНФ (или СДНФ) по правилу Блейка
Применение этого правила состоит из двух частей:
— если среди дизъюнктных слагаемых в ДНФ имеются слагаемые 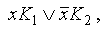
— если добавляемое слагаемое уже содержалось в ДНФ, то его можно отбросить совсем, например,
Разумеется, сокращенная ДНФ не определяется единственным образом, но все они содержат одинаковое число букв (например, имеется ДНФ 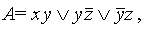
в) переход от ДНФ к СДНФ
Если в какой-то простой конъюнкции недостает переменной, например, z, вставляем в нее выражение 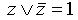
г) переход от КНФ к СКНФ
Этот переход осуществляется способом, аналогичным предыдущему: если в простой дизъюнкции не хватает какой-то переменной (например, z, то добавляем в нее выражение 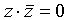
Таким образом, из КНФ получена СКНФ.
Заметим, что минимальную или сокращенную КНФ обычно получают из соответствующей ДНФ.
Совершенная нормальная форма — дизъюнктивная и конъюнктивная, правило построения
Что такое СДНФ
Нормальная форма логической формулы характеризуется тем, что для нее не свойственны эквивалентность, отрицание формул неэлементарного типа и знаки импликации.
Существует две формы нормального типа: КНФ (конъюнктивная нормальная форма) и ДНФ (дизъюнктивная нормальная форма).
СДНФ — совершенная дизъюнктивная нормальная форма формулы. СДНФ — способ написания функции алгебры логики в качестве логического выражения.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
СДНФ формулы — это равнозначная ей формула, которая представляет собой дизъюнкцию элементарных конъюнкций, при которых функция достигает показателя «1».
ДНФ выглядит следующим образом:
СДНФ обладает некоторыми определенными свойствами:
К СДНФ возможно привести любую формулу алгебры логики. Исключение составляет только тождественно ложная формула. СДНФ можно получить как используя таблицы истинности, так и через равносильные преобразования.
При построении таблицы истинности важно помнить, что логические переменные со значением «0» необходимо брать с отрицанием.
Что такое СКНФ
СКНФ — совершенная конъюнктивная нормальная форма. Формулу можно назвать таковой, когда она — конъюнкция неповторяющихся элементарных дизъюнкций.
Формула должна соответствовать нескольким условиям, чтобы называться СКНФ:
Правила построения по таблице истинности
Дизъюнктивная форма
Если функция равна 1, то для всех наборов переменных, при которых это происходит, записывается произведение. Однако переменные, которые имеют значение 0, берутся с отрицанием.
Конъюнктивная форма
Когда функция равна 0, то для всех наборов переменных, при которых это происходит, записывается сумма. Однако переменные, которые имеют значение 1, берутся с отрицанием.
Алгоритм приведения к СДНФ и СКНФ
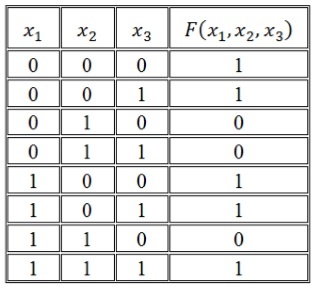
Рассмотрим логическую функцию в виде таблицы истинности.
Алгоритм построения СДНФ по таблице истинности выглядит следующим образом:
Построим совершенную ДНФ:
И как результат получим следующую СДНФ:
Алгоритм построения СКНФ по таблице истинности выглядит следующим образом:
Построим совершенную КНФ:
И как результат получим следующую СКНФ:
Рассмотрев алгоритмы построения СДНФ и СКНФ ясно, что в случае подавляющей части наборов значений переменных функция равна 0, то значительно легче построить и СДНФ для получения ее формулы, а в обратном случае — СКНФ.
Доказательство эквивалентности
Доказать эквивалентность формул можно двумя способами.
Далее следуют примеры с некоторыми эквивалентными преобразованием в булевой алгебре и новыми эквивалентностями, которые возможно получить с их помощью.
Поглощение
Склеивание
Обобщенное склеивание
\(xz\;\vee\;y\overline z\;\vee\;xy\;=\;xz\;\vee y\overline z\)
\(xz\;\vee\;y\overline z\;\vee\;xy\;=\;xz\;\vee y\overline z\;\vee\;xyz\;\vee\;xy\overline z\;=\;xz\;\vee\;y\overline z\)
Расщепление
\(x\;\vee\;\overline xy\;=\;xy\;\vee\;x\overline y\;\vee\;\overline xy\;=\;xy\;\vee\;x\overline y\;\vee\;xy\;\vee\;\overline xy\;=\;x\;\cdot\;l\;\;\vee\;y\;\cdot\;l\;=\;x\;\vee\;y\)
Примеры с решением
Задача №1
Через применение закона де Моргана и правила \( x\;\rightarrow\;y\;=\;\overline x\;\vee\;y\) упростим выражения:
\(F\;=\;((((A\;\rightarrow\;B)\;\rightarrow\;\overline A)\;\rightarrow\overline B)\;\rightarrow\;\overline C)\;=\;(((\overline A\;\vee\;B)\;\rightarrow\;\overline A)\;\rightarrow\;\overline B)\;\rightarrow\overline C\;)\;=\)
\(=\;((((\overline A\;\vee\;B)\;\rightarrow\overline A)\;\rightarrow\overline B)\;\rightarrow\;\overline C)\;=\;((\overline<((\overline A\;\vee\;B)>\;\vee\;\overline A)\;\rightarrow\overline B)\;\rightarrow\overline C)\;=\)
\(=(((\overline A\;\vee\;B)\;\vee\;\overline A)\;\rightarrow\;\overline B)\;\rightarrow\;\overline C)\;=((\overline<(\overline<(\overline A\vee B)>\;\vee\;\overline A\;)>\;\vee\;\overline B)\;\rightarrow\;\overline C)\;=\)
\(=\;((\overline<(\overline A\;\vee\;B)>\;\vee\;\overline A)\;\wedge\;B)\;\vee\;\overline C\;=\;(((A\;\wedge\;\overline B)\;\vee\;\overline A)\;\wedge B)\;\vee\;\overline C\;=\)
\(=((A\overline B\;\vee\;\overline A)\;\vee\;\overline A)\;\wedge\;B)\;\vee\;\overline C\;=(((A\;\wedge\;\overline B)\;\vee\;\overline A)\;\wedge\;B)\;\vee\;\overline C\;=\)
\(=\;((A\overline B\;\vee\;\overline A)\;\wedge\;B)\;\vee\;\overline C\;=\;(A\overline BB\;\vee\;\overline AB)\;\vee\;\overline C\;=\;(0\;\vee\;\overline AB)\;\vee\;\overline C\;=\;\overline AB\;\vee\;\overline C\)
Далее приведем выражение к КНФ:
\(F\;=\;\overline AB\;\vee\;\overline C\;\;=\;(\overline A\;\vee\;\overline C)\;\wedge\;(B\;\vee\;\overline C)\)
Далее приведем выражение к СКНФ:
\(F\;=\;(\overline A\;\vee\;\overline C)\;\wedge\;(B\;\vee\;\overline C)\;=\;(\overline A\;\vee\:\overline C\;\vee\;B\overline B)\;\wedge\;(A\overline A\;\vee\;B\;v\;\overline C)\;=\)
\(=\;(\overline A\;\vee\;\overline C\;\vee\;B)\;\wedge\;(A\;\vee\;B\;\vee\;\overline C)\;\wedge\;(\overline A\;\vee\;\overline C\;\vee\;\overline B)\;\wedge\;(\overline A\;\vee\;B\;\;\overline C)\)
Задача №2
Используя эквивалентные преобразования, постройте ДНФ функции \(f(\widetilde x^n)\)
\(f(\widetilde x^3) = (\overline
\(f(\widetilde x^3) = (\overline
\(=(\overline
ДНФ, СДНФ, КНФ, СКНФ
Простой конъюнкцией называется конъюнкция одной или нескольких переменных, при этом каждая переменная встречается не более одного раза (либо сама, либо ее отрицание).
Например, 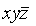
Дизъюнктивной нормальной формой (ДНФ) называется дизъюнкция простых конъюнкций.
Например, выражение 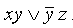
Совершенной дизъюнктивной нормальной формой (СДНФ) называется такая дизъюнктивная нормальная форма, у которой в каждую конъюнкцию входят все переменные данного списка (либо сами, либо их отрицания), причем в одном и том же порядке.
Например, выражение 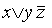
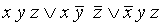
Аналогичные определения (с заменой конъюнкции на дизъюнкцию и наоборот) верны для КНФ и СКНФ. Приведем точные формулировки.
Простой дизъюнкцией называется дизъюнкция одной или нескольких переменных, при этом каждая переменная входит не более одного раза (либо сама, либо ее отрицание).Например, выражение 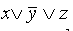
Конъюнктивной нормальной формой (КНФ) называется конъюнкция простых дизъюнкций (например выражение 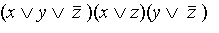
Совершенной конъюнктивной нормальной формой (СКНФ) называется такая КНФ, у которой в каждую простую дизъюнкцию входят все переменные данного списка (либо сами, либо их отрицания), причем в одинаковом порядке.
Например, выражение 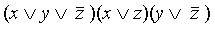
Приведем алгоритмы переходов от одной формы к другой. Естественно, что в конкретных случаях (при определенном творческом подходе) применение алгоритмов бывает более трудоемким, чем простые преобразования, использующие конкретный вид данной формы:
а) переход от ДНФ к КНФ
Алгоритм этого перехода следующий: ставим над ДНФ два отрицания и с помощью правил де Моргана (не трогая верхнее отрицание) приводим отрицание ДНФ снова к ДНФ. При этом приходится раскрывать скобки с использованием правила поглощения (или правила Блейка). Отрицание (верхнее) полученной ДНФ (снова по правилу де Моргана) сразу дает нам КНФ:
Заметим, что КНФ можно получить и из первоначального выражения, если вынести у за скобки;
б) переход от КНФ к ДНФ
Этот переход осуществляется простым раскрытием скобок (при этом опять-таки используется правило поглощения)
Таким образом, получили ДНФ.
Обратный переход (от СДНФ к ДНФ) связан с проблемой минимизации ДНФ. Подробнее об этом будет рассказано в разд. 5, здесь же мы покажем, как упростить ДНФ (или СДНФ) по правилу Блейка. Такая ДНФ называется сокращенной ДНФ;
в) сокращение ДНФ (или СДНФ) по правилу Блейка
Применение этого правила состоит из двух частей:
— если среди дизъюнктных слагаемых в ДНФ имеются слагаемые 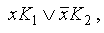
— если добавляемое слагаемое уже содержалось в ДНФ, то его можно отбросить совсем, например,
Разумеется, сокращенная ДНФ не определяется единственным образом, но все они содержат одинаковое число букв (например, имеется ДНФ 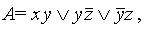
в) переход от ДНФ к СДНФ
Если в какой-то простой конъюнкции недостает переменной, например, z, вставляем в нее выражение 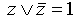
г) переход от КНФ к СКНФ
Этот переход осуществляется способом, аналогичным предыдущему: если в простой дизъюнкции не хватает какой-то переменной (например, z, то добавляем в нее выражение 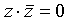
Таким образом, из КНФ получена СКНФ.
Заметим, что минимальную или сокращенную КНФ обычно получают из соответствующей ДНФ.
4. Представление логических функций
в виде СДНФ (СКНФ)
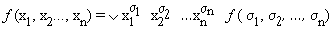
а) Пусть f(x1, x2, …, xn)= 1. Тогда слева в формуле (* ) стоит 1. Докажем, что и справа в этом случае стоит 1, для чего достаточно указать одно дизъюнктное слагаемое, равное 1. Но среди всех наборов (s1, s2, …, sп) имеется набор s1 = х1, s2 = х2, …, sп = хп. Очевидно, что для этого набора слагаемое 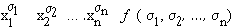
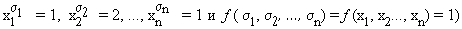
б) Пусть f(x1, x2, …, xn) = 0. Предположим, что справа стоит не ноль, а единица, тогда какое-то слагаемое тоже должно равняться 1, т. е. для некоторого набора
Доказательство. Пусть f(x1,x2,…,xn) не равна тождественному нулю, тогда в дизъюнкции можно не записывать слагаемые, равные нулю, а из формулы (* ) следует следующее представление для данной функции
Следствие. Любую логическую (булеву) функцию можно выразить через три логические функции: конъюнкцию, дизъюнкцию и отрицание.
Набор функций, через которые можно выразить любые другие функции, называется полным набором (более точные формулировки даны в разд. 7). Таким образом, конъюнкция, дизъюнкция и отрицание являются полным набором.
По аналогии с представлением любой функции (не равной тождественному нулю) в виде СДНФ можно функцию (не равную тождественной 1) представить в виде СКНФ: простая дизъюнкция составляется для тех наборов переменных (х1, х2, …, хп), для которых f(x1, x2,…, xn) = 0, причем если хi = 1, то в этой дизъюнкции берем 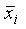
Пример. Составить для импликации и сложения по модулю 2 СДНФ и СКНФ.
Тогда СДНФ для этих функций:
СКНФ для этих функций:
5. Нахождение сокращенной ДНФ
по таблице истинности (карты Карно)
Доказано, что любую функцию (кроме тождественного нуля) можно представить в виде СДНФ. На практике часто бывает удобно получить (вместо СДНФ) как можно более “короткую” ДНФ. Словам “короткая ДНФ” можно придать разный смысл, а именно:
ДНФ называется минимальной, если она содержит наименьшее число букв (разумеется, среди всех ДНФ ей равносильных); ДНФ называется кратчайшей, если она содержит минимальное число знаков дизъюнкции Ú ; тупиковой, если уничтожение одной или нескольких букв в ней приводит к неравной ДНФ и сокращенной ДНФ, если ее упрощение проведено с помощью правила Блейка.
На практике наиболее важной представляется нахождение минимальной ДНФ, но алгоритм ее нахождения по существу является вариантом перебора всех равносильных ДНФ. Алгоритмически проще всего находить сокращенную ДНФ (эти алгоритмы были даны в разд. 3). Заметим, что если функция п переменныхзаданасвоейтаблицей истинности, топравило Блейка имеет простой геометрический смысл. Именно, если все возможные наборы переменных представить себе как вершины п-мерного куба со стороной равной 1 (всего вершин будет 2 п ) в декартовой системе координат, то надо отметить те вершины, на которых значение функции равно 1, и если какие-то из этих единиц лежат на “прямой”, “плоскости” или “гиперплоскости” в п-мерном пространстве, то в сокращенную ДНФ будут входить “уравнения” этих прямых или гиперплоскостей по известному правилу: если в это уравнение входило составной частью х = 0,то в сокращенную ДНФ входит 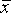
Карты Карно позволяют эти геометрические идеи использовать при п = 3, 4, 5, для функций, заданных своей таблицей истинности. При больших п картыКарнопрактическинеиспользуются. Рассмотрим отдельно (и более подробно) случаи п = 3, 4.
Составляем таблицу истинности для данной конкретной функции п = 3 в виде таблицы, приведенной в примере 5.1. (Заметим, что для х1и х2естественный порядок набора переменных здесь нарушен. Это сделано для того, чтобы при переходе от данного к следующему набору переменных в этом наборе менялась только одна цифра). Прямая содержит 2 вершины, плоскость – 4, гиперплоскости – 8, 16 и т. д. вершин, поэтому объединять можно 2 рядом стоящие единицы или 4, 8, 16 и т. д. Карты Карно соединяются “по кругу”, т. е. наборы (10) и (00) считаются рядом стоящими.
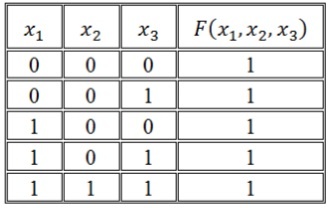
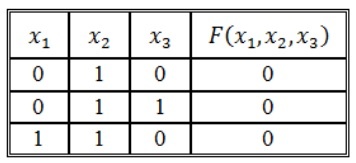
Пример 5.1. Пусть задана функция:
Видно, ее СДНФ содержит (по числу 1) 6 дизъюнктных слагаемых, но ее сокращенная ДНФ содержит (после объединения единиц) всего 2 буквы
Пример 5.2. Следующий пример показывает, “как соединять единицы по кругу”.
Здесь сокращенная ДНФ содержит 2 слагаемых (СДНФ содержала бы 5):
Пример 5.3. Пример показывает использование карт Карно при п = 4.
Здесь сокращенная ДНФ содержит 4 слагаемых (СДНФ содержит 8):
При п = 5 использование карт Карно является несколько более сложным и здесь не приводится.