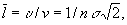Что такое длина свободного пробега электрона
длина свободного пробега
— полное эфф. сечение столкновений,
угл. скобки означают усреднение по Максвелла распределению относительных скоростей с приведённой массой 
-дифференц. эфф. сечение столкновения. При вычислении кинетических коэф. оказываются существенными т. н. транспортные Д. с. п. Напр., для диффузии вводят транспортное эфф. сечение
Понятие Д. с. п. удобно для качеств. рассмотрения явлений переноса в газах, оно обобщено на случай систем слабовзаимодействующих частиц: электронный газ в металлах и полупроводниках, нейтроны в слабопоглощающих средах и т. п.
Лит.: Чепмен С., Каулинг Т., Математическая теория неоднородных газов, пер. с англ., M., 1960, гл.5; Ферцигер Д да., Капер Г., Математическая теория процессов переноса в газах, пер. с англ., M., 1976, гл. 2, 14. Д. H. Зубарев.
С помощью Д. с. п. производятся аналитич. оценки кинетических коэф. газов и плазмы.
Лит.: Смирнов Б. M., Физика слабоионизованного газа, M., 1972; Лифшиц E. M., Питаевский Л. П., Физическая кинетика, M., 1979. Л. П. Пресняков.
ДЛИНА СВОБОДНОГО ПРОБЕГА
— полное эфф. сечение столкновений,
угл. скобки означают усреднение по Максвелла распределению относительных скоростей с приведённой массой 
-дифференц. эфф. сечение столкновения. При вычислении кинетических коэф. оказываются существенными т. н. транспортные Д. с. п. Напр., для диффузии вводят транспортное эфф. сечение
Понятие Д. с. п. удобно для качеств. рассмотрения явлений переноса в газах, оно обобщено на случай систем слабовзаимодействующих частиц: электронный газ в металлах и полупроводниках, нейтроны в слабопоглощающих средах и т. п.
Лит.: Чепмен С., Каулинг Т., Математическая теория неоднородных газов, пер. с англ., M., 1960, гл.5; Ферцигер Д да., Капер Г., Математическая теория процессов переноса в газах, пер. с англ., M., 1976, гл. 2, 14. Д. H. Зубарев.
С помощью Д. с. п. производятся аналитич. оценки кинетических коэф. газов и плазмы.
Лит.: Смирнов Б. M., Физика слабоионизованного газа, M., 1972; Лифшиц E. M., Питаевский Л. П., Физическая кинетика, M., 1979. Л. П. Пресняков.
Длина свободного пробега
Содержание
Расчет по поперечному сечению и плотности частиц
Оценка для газов
σ geom знак равно π d 2 <\ displaystyle \ sigma _ <\ text 
Геометрическая длина свободного пробега следует из этого
⇒ λ geom знак равно 1 π п d 2 <\ displaystyle \ Rightarrow \ lambda _ <\ text
Приведенная выше интерпретация применима, когда партнеры по столкновению летящей частицы находятся в состоянии покоя.
Определение двух типов частиц
В области пространства, содержащей два типа частиц, возможны три типа столкновения:
Длина свободного пробега для столкновений между частицами в каждом случае уже определяется с помощью приведенной выше формулы:
Длина свободного пробега частицы типа 2 в среде типа 1 определяется соответственно:
или аналогично, когда частица типа 1 сталкивается со средой типа 2: λ 12 <\ displaystyle \ lambda _ <12>>
поперечное сечение в обоих случаях одинаковое. σ 12 <\ displaystyle \ sigma _ <12>>
Поперечное сечение и длина свободного пробега двух разных частиц в большинстве случаев не имеют индекса или других символов разметки, написанных так и : σ знак равно σ 12 <\ displaystyle \ sigma = \ sigma _ <12>> λ знак равно λ 21-е <\ displaystyle \ lambda = \ lambda _ <21>>
Оценка столкновения двух типов частиц
Геометрическое сечение упругого столкновения двух жестких сфер радиусом или равно р 1 <\ displaystyle r_ <1>> р 2 <\ displaystyle r_ <2>>
σ geom знак равно π ( р 1 + р 2 ) 2 <\ displaystyle \ sigma _ <\ text
Таким образом, средняя геометрическая длина свободного пробега составляет:
⇒ λ geom знак равно 1 π п 1 ( р 1 + р 2 ) 2 <\ displaystyle \ Rightarrow \ lambda _ <\ text
Геометрическое сечение и, следовательно, геометрическая длина свободного пробега упругого рассеяния не зависят от кинетической энергии сфер. С другой стороны, реальные эффективные сечения и, следовательно, длина свободного пробега могут сильно зависеть от кинетической энергии партнеров столкновения и, следовательно, не обязательно определяются вышеизложенным. рассчитать простую геометрическую модель. Однако даже в случае реальных поперечных сечений может быть полезно использовать геометрическое поперечное сечение в качестве эталонного значения, например: реальное поперечное сечение в 10 раз больше геометрического, тогда реальная длина свободного пробега составляет лишь десятую часть геометрического.
Столкновения нейтронов и ядер атомов
Величина, обратная длине свободного пробега этого типа, является одной из важнейших величин в физике реакторов под названием макроскопического сечения :
Сечения ядерных реакций чрезвычайно сильно зависят от энергии и поэтому больше не могут быть объяснены геометрически. Только в случае упругого рассеяния нейтронов на атомных ядрах обычных замедлителей указанная выше геометрическая модель приводит к длинам свободного пробега, которые находятся в порядке величины измеренных значений; это по крайней мере для нейтронов с кинетической энергией в определенном среднем интервале.
Примеры
Молекулы газа
В следующей таблице приведены приблизительные значения длины свободного пробега молекул газа при различных давлениях:
Электроны
Длина свободного пробега свободных электронов важна при использовании электронных пучков в вакууме (например, для некоторых поверхностно-чувствительных аналитических методов или в трубках Брауна ). Это зависит от кинетической энергии электрона.
Большая Энциклопедия Нефти и Газа
Длина свободного пробега электрона обратно пропорциональна вероятности рассеяния электр она внутри кристаллической решетки полупроводника. Мерой такой вероятности служит степень отступления от строгой периодичности идеальной кристаллической решетки. [1]
Длина свободного пробега электронов весьма мала. Поэтому электроны под действием поляне успевают приобрести большой скорости; их средняя скорость упорядоченного ( создаваемого полем) движения и во много раз меньше средней скорости v их теплового движения. [3]
Длина свободного пробега электронов в металле определяется волновыми свойствами электронов. [4]
Длина свободного пробега электрона в пленке ограничивается не только ее поверхностью, но и структурными дефектами. На структуру пленки влияет температура подложки в момент осаждения, поэтому удельное сопротивление зависит от температуры подложки, уменьшаясь с возрастанием температуры. Снижение удельного сопротивления наблюдается у пленок, полученных на холодной подложке после прогрева в вакууме. Температура структурных превращений пленок близка к температуре рекристаллизации металла и существенно зависит от толщины пленок. Степень изменения удельного сопротивления после прогрева у тонких пленок более велика, чем у толстых. [5]
Газокинетическая длина свободного пробега электрона Ае дает лишь приближенное представление о движении электронов в газе. Qe) оказывается зависящим также от скорости движения ( энергии) электронов. Здесь скорость электрона V3 см / сек связана с энергией электрона U3 эв соотношением v3 6 107 Уиз. [7]
Если длина свободного пробега электронов превышает расстояние между электродами, то движение электронов можно рассматривать как свободное. Теплопередача сводится к переносу энергии электронами и к лучеиспусканию. [8]
Понятие длина свободного пробега электронов и ее зависимость от кинетической энергии теряет смысл для таких ионных полупроводников, в которых длина пробега оказывается меньше межатомных расстояний. Длина волны электронов здесь превышает размеры рассеивающих центров, а неопределенность в значении кинетической энергии на порядок величины больше самой энергии. [9]
Обычно длина свободного пробега электрона в полупроводнике значительно меньше толщины электронно-дырочного перехода. Если за время свободного пробега электроны успевают набрать достаточную энергию, то возникает ударная ионизация атомов электронами. Поскольку скорость электронов, определяющая их энергию, зависит от напряженности электрического поля: vn inE, для ударной ионизации необходима определенная величина этой напряженности. [10]
Когда длина свободного пробега электрона начинает ограничиваться примесями и дефектами, она становится температурно независящей и сопротивление, которое и называется остаточным, становится практически постоянной величиной. В неупорядоченных сплавах даже при комнатной температуре сопротивление может обусловливаться главным образом неоднородностями. [11]
Если длина свободного пробега электронов превышает расстояние между электродами, то движение электронов можно рассматривать как свободное. Теплопередача сводится к переносу энергии электронами и к лучеиспусканию. [12]
Вычисление длины свободного пробега электронов проводимости в металлах при комнатной температуре дает величину в несколько сотен ангстрем. Таким образом, в этом интервале толщин электроны проводимости в пленках будут чаще сталкиваться с поверхностью пленки, чем с другими центрами рассеяния, и рассеяние на поверхности становится важным механизмом для сопротивления. Так как этот механизм рассеяния не чувствителен к деформации, в целом чувствительность к деформации уменьшается. Если еще дальше уменьшать толщину пленки, пленка перестает быть сплошной, и общее сопротивление начинает определяться сопротивлением участков между отдельными островками. [15]
Длина свободного пробега
Длина́ свободного пробега
(точнее — средняя длина свободного пробега, `l)
средняя длина пути, проходимого частицей между двумя последовательными соударениями с др. частицами. Понятием Д. с. п. широко пользуются при расчётах различных процессов переноса, например вязкости, теплопроводности, диффузии, электропроводности и др.
Согласно кинетической теории газов, молекулы от столкновения до столкновения движутся равномерно и прямолинейно. Если за 1 сек молекула проходит в среднем путь v, испытывая при этом ν упругих соударений с такими же молекулами, то
где n — число молекул в единице объёма (плотность газа), σ — Эффективное поперечное сечение молекулы. С повышением плотности газа (его давления) Д. с. п. уменьшается, т.к. растет число столкновений ν в 1 сек. Повышение температуры (интенсивности движения молекул) приводит к некоторому уменьшению σ и, следовательно, к росту `l. Для обычных молекулярных газов в нормальных условиях (См. Нормальные условия) (при атмосферном давлении и 20°С) `l
К частицам, движение и взаимодействие которых подчиняется законам квантовой механики (См. Квантовая механика), понятие Д. с. п. в ряде случаев также применимо (например, электроны проводимости в твёрдом теле, Нейтроны в слабо поглощающих средах, Фотоны в звёздах), но расчёт Д. с. п. для таких частиц более сложен.