Что такое длина отрезка в геометрии 7 класс
Отрезок
Определение отрезка
Определение 1. Отрезок (или отрезок прямой )− это часть прямой, ограниченная двумя точками.
Определение 2. Отрезок − это множество, состоящая из двух различных точек данной прямой и всех точек, лежащих между ними.
Точки, ограничивающие отрезки называются концами отрезка, а точки, которые находятся между концами отрезка называются внутренними точками.
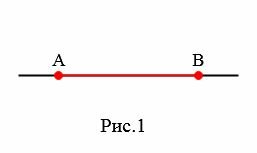 |
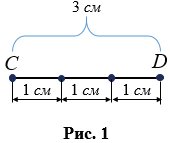
На рисунке 1 отрезок выделен красным цветом. Точки A и B концы отрезка, а точки между ними − внутренние точки.
Обозначение отрезков
Отрезки обозначаются с помощью его конечных точек. Отрезок на рисунке 1 обозначается так: AB или BA. Порядок следования имен конечных букв не имеет значения.
Сравнение отрезков
Для сравнения отрезков нужно:
Если два других конца совместяться, то отрезки равны. Если же конец одного отрезка находится внутри другого, то длина первого отрезка меньше второго.
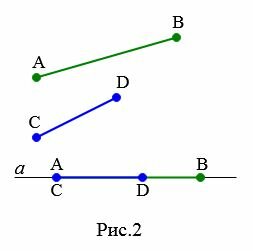 |
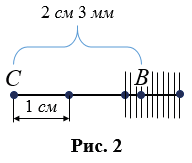
Пусть даны два отрезка AB и CD (Рис.2). Требуется сравнить эти отрезки, т.е. определить какой из них больше. Отложим эти отрезки на прямой a. Как видим, точка D находится внутри отрезка AB. Значит отрезок CD меньше отрезка AB. Это обозначается так: CD Определение 3. Точка отрезка,делящая его на два равных отрезка называется серединой отрезка.
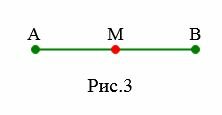 |
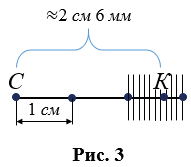
На рисунке 3 \( \small M \) является серединой отрезка \( \small AB \) поскольку \( \small AM = MB \).
Длина отрезка
Для определения длины отрезка его нужно сравнить с другим отрезком, принятым за единицу измерения.
В качестве единицы измерения можно взять, например, сантиметр. В этом случае для определения длины отрезка узнают, сколько раз в данном отрезке укладывается сантиметр. Этот показатель и является длиной отрезка выраженная в сантиметрах. Если длина отрезка AB равна трем сантиметрам, то пишут AB=3см.
Если отрезок, принятый за единицу измерения не укладывается целое число раз в измеряемом отрезке, то его обычно делят на 10 равных частей и определяют сколько раз одна такая часть укладывается в остатке. Одна десятая часть сантиметра называется миллиметром. В итоге получаем длину отрезка в сантиметрах и миллиметрах.
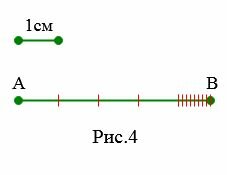 |
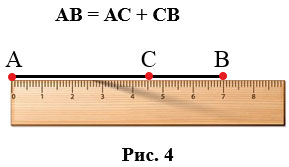
На Рис.4 1см укладывается в отрезке AB 4 раза и в остатке укладывается ровно 8 одну десятую часть сантиметра. Поэтому можно писать: AB=4см 8мм или AB=4.8см.
Направленный отрезок
Если для отрезка определить направление, то такой отрезок называется направленным отрезком. Направленный отрезок имеет начальную точку и конечную точку. В конечной точке направленного отрезка рисуют стрелку (Рис.5)
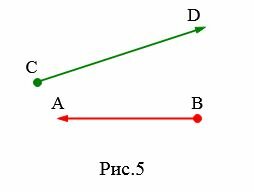 |
Для обозначения направленных отрезков сначала пишется начальная точка, а затем конечная точка. На рисунке 2 верхний направленный отрезок обозначают так: \( \small \overrightarrow
Отрезок
Отрезок — это часть прямой, ограниченная двумя точками, лежащими на этой прямой. Точки, определяющие границы отрезка, называются концами отрезка.
Отрезок обозначается двумя большими латинскими буквами, поставленными при его концах: отрезок AB или BA.
Длина отрезка
Длина отрезка — это расстояние между концами отрезка. Любой отрезок имеет длину, бо́льшую нуля:
Измерение длины отрезка осуществляется путём сравнения данного отрезка с длиной единичного отрезка. Единичный отрезок — это отрезок, длина которого принимается за единицу. Следовательно:
длина отрезка – это положительное число, показывающее, сколько раз единичный отрезок и его части укладываются в данном отрезке.
Чаще всего используются единичные отрезки равные 1 мм, 1 см, 1 дм, 1 м или 1 км. Измерить длину отрезка можно линейкой или любым другим прибором для измерения длины:
Свойства длин отрезков:
Равные отрезки
Равные отрезки — это отрезки, имеющие одинаковую длину. Если наложить равные отрезки друг на друга, то их концы совпадут.
Пример. Возьмём два отрезка CD и LM:
Если расположить отрезки параллельно друг над другом так, чтобы точка C была над точкой L, то станет видно, что точка D располагается над точкой М:
Значит длины отрезков равны, следовательно CD = LM.
Сравнение отрезков
Сравнить два отрезка — это значит определить, равны они, или один больше другого.
Сравнить два отрезка можно, отложив на прямой оба отрезка из одной точки в одну и туже сторону. Для этого можно воспользоваться циркулем.
Чтобы отложить на прямой отрезок равный данному, сначала помещают ножки циркуля так, чтобы острия их концов упирались в концы отрезка, а затем, не изменяя раствора циркуля, переносят его так, чтобы оба его конца находились на прямой.
При сравнении двух отрезков возможно получение одного из представленных результатов: отрезки будут равны, первый отрезок будет больше второго или первый отрезок будет меньше второго.
Пример. Если отложить на прямой от любой точки, например C, в одну сторону два отрезка CA и CB и точка A окажется между точками C и B, то отрезок CA меньше отрезка CB (или CB больше отрезка CA):
Если точка B окажется между точками C и A, то отрезок CA больше отрезка CB (или CB меньше отрезка CA):
CA > CB или CB Пример. Сравнить длину отрезков AB и AC.
Так как отрезок AB имеет большую длину, чем отрезок AC, то
Так как отрезки AB и AC имеют одинаковую длину, то
Если при измерении отрезков их длины равны, то и отрезки равны.
Середина отрезка
Середина отрезка — это точка, делящая отрезок на две равные части.
Длина отрезка
Для того, чтобы найти длину отрезка, его сравнивают с отрезком принятым за единицу измерения, который носит название единичный отрезок.
Если за единицу измерения принять сантиметр, то, чтобы определить длину отрезка, нужно узнать сколько раз в этом отрезке укладывается сантиметр. На рис.1 в отрезке СD сантиметр укладывается ровно три раза, значит, длина отрезка СD равна 3 см, можно записать СD = 3 см. В данном случае, для измерения удобно использовать сантиметровую линейку.
Бывает, что единичный отрезок не укладывается целое число раз в измеряемый отрезок, тогда единичный отрезок делят на 10 равных частей и определяют сколько раз одна десятая часть укладывается в остатке измеряемого отрезка. На рис.2 в отрезке СВ сантиметр укладывается 2 раза и в остатке 3 раза укладывается одна десятая часть сантиметра, значит, длина отрезка СВ равна 3,3 см или, учитывая что для сантиметра десятая часть равна миллиметру, 3 см 3 мм, т.е. можно записать СВ = 3,3 см (СВ = 3 см 3 мм).
Может получится так, что и в миллиметрах остаток не укладывается целое число раз, тогда:
За единицу измерения можно принимать не только сантиметр, но и другие отрезки, например, дециметр, метр и т.д.
Свойства длин отрезков:
Поделись с друзьями в социальных сетях:
Урок геометрии в 7-м классе по теме: «Длина отрезка. Единицы измерения»
Разделы: Математика
Измерь самого себя – и ты станешь настоящим геометром!
1. Поговорим об измерениях.
И тема урока сегодня: Длина отрезка. Единицы измерения.
В повседневной жизни нам часто приходится сталкиваться с измерением длины высот, расстояний. С точки зрения геометрии мы имеем в таких случаях дело с измерением отрезков.
Один средневековый философ Марсилио Сичино сказал: «Измерь самого себя – и ты станешь настоящим геометром!» Конечно, измерить самого себя и стать настоящим Геометром, настоящим Садовником, настоящим Поэтом и вообще Настоящим очень трудно. Но если говорить о чем-то более простом, то с уверенностью можно сказать что каждому человеку, научившемуся считать и писать, неоднократно приходилось что-то измерять: высоту дерева, собственный вес, длину прыжка, время бега и многое другое.
И все же давайте подумаем над вопросом: «что значит – измерить какую-то величину?»
2. Единицы измерения длины в разное время и странах.
Любые измерения производят в каких-то единицах: длины – измеряют в единицах длины, вес – в единицах веса и т.д. С незапамятных времен человеку приходилось измерять расстояния в связи с изготовлением простейших орудий труда, со строительством жилищ и с добыванием пищи.
За свою историю человечество придумало огромное количество всевозможных единиц, причем каждый народ имел свои. Как известно, герои одного мультфильма измеряли длину удава в попугаях. Для обитателей тропического леса, в котором живет попугай, эта единица ни чуть не хуже других. Но длина в попугаях ничего не скажет жителям тайги.
Эта история из мультфильма не такая уж нелепая. Правители разных стран любили устанавливать свои меры, часто связанные с собственной персоной. Например, английский король Генрих I ввел в качестве единиц длины ЯРД – расстояние от кончика своего носа до большого пальца вытянутой руки.
Более демократична по происхождению другая английская единица длины ФУТ, что по-английски означает «ступня». 16 англичан выстраивались в цепочку таким образом, что каждый следующий касался концами пальцев своих ног пяток предыдущего. 1/16 такой цепочки и составляла 1 фут.
На Руси в старину мерами длины были ШАГ,
ПЯДЬ: Малая пядь равнялась расстоянию между концами растянутых пальцев, большего и указательного (
19 см), большая пядь – расстояние между раздвинутым большим пальцем и мизинцем (
ЛАДОНЬ – ширина кисти руки, ЛОКОТЬ – расстояние от локтя до конца среднего пальца.
Аршин делился на 16 вершков, 3 аршина составляли САЖЕНЬ – расстояние от ступни до конца среднего пальца вытянутой руки,
500 саженей – составляли ВЕРСТУ (или поприще), 7 верст – МИЛЮ. Таким образом, при раздроблении и превращении приходилось умножать, соответственно делить на разные числа: 16, 3, 500, 7. Между тем практика измерений и вычислений показала, что проще и удобнее пользоваться такими мерами, у которых отношение двух ближайших единиц было бы постоянным и равнялось бы именно десяти – основанию нумерации.
Метрическая система мер отвечает этим требованиям. Но о ней мы сегодня говорить не будем, вы можете узнать о ней на уроках физики.
Многим известно старинное пожелание морякам: «Семь футов под килем!»
А сколько это будет аршин; метров?
3. Эталоны.
С развитием производства и торговли люди убедились в том, что не всегда удобно измерять расстояния шагами или прикладыванием локтя. Кроме того, такое измерение уже не удовлетворяло возросшим требованиям точности. В самом деле, длина локтя или шага у разных людей различная, а мера длины должна быть постоянной. Постоянные образцы мер стали изготавливать из деревянных линеек и металлических стержней.
Образцы мер в настоящее время называются эталонами.
Вернемся к вопросу, заданному в начале: «Что значит измерить?»
Коротко можно ответить так: «Измерить – значит сравнить с эталоном».
4. Свойства длины отрезка.
Попробуем выяснить некоторые правила длины:
Вот и первое правило: Длина отрезка выражается положительным числом.
— Начертите два равных отрезка, измерьте их длины, сравните.
— Начертите еще два равных отрезка, измерьте и сравните.
Вот и второе: Равные отрезки имеют равные длины.
— Начертите отрезок АВ, между точками А и В поставьте точку С, что получилось? Измерьте АС и СВ, найдите сумму, измерьте АС. Что получили?
И третье: Когда точка делит отрезок на два отрезка, длина всего отрезка равна сумме длин этих двух отрезков.
— А чем мы обычно измеряем? Сравниваем?
К древнейшим геометрическим инструментам относятся циркуль и линейка. Употребление линейки берет свое начало с незапамятных времен. Циркуль был изобретен значительно позже. Фигуры папируса Ахмеса, например, свидетельствует о применении линейки, но не циркуля. Согласно римскому поэту Овидию (I век) циркуль был изобретен в древней Греции.
В техническом черчении употребляют масштабную миллиметровую линейку. Для измерения диаметра трубки используют штангенциркуль.
Для измерения расстояний на местности пользуются рулеткой.
В книге Памелы Л. Трэверс «Мэри Поппинс» в одном из эпизодов Кошка задает вопросы Королю. «Первый вопрос: «Высоко ли до неба?» Король удовлетворенно хмыкнул. Это был вопрос как раз в его вкусе, и он улыбнулся с видом превосходства.
К сожалению, я вынуждена прервать цитату. Желающие могут прочесть книгу и узнать, чем закончился этот разговор. Как ни странно, но Король прав. Задача измерения весьма трудная, и одной изобретательности не достаточно. Надо многое знать.
Решим и мы несколько задач на измерение отрезков.
1) На отрезке АС поставлена точка В, АВ=4,2 см, ВС=1,3 см. Найдите длину АС.
2) На отрезке АВ лежит точка С, АС=6,1 см, АВ=8,7 см. Найдите длину СВ.
3) На отрезке LS лежат точки K и R так, что К лежит между L и R, LK=3,5 см, LS=9 см и LK=KR. Найти RS.
4) (Устно) Точка М лежит на прямой ЕF между Е и F. Чему равна длина отрезка МF, если EF=7,2 cм, EM=2,2 cм?
7. «Живой метр».
Приятно и полезно уметь не только измерять расстояния без мерной линейки, шагами, но и оценивать их прямо на глаз. Этот навык можно выработать только путем упражнений.
Любопытно, что глазомер как будто не зависит от остроты зрения. И близорукие могут точно определять расстояния.
Можно упражняться в глазомерной оценке в любое время года, в любой обстановке.
Хорошо бы каждому из нас обзавестись таким «живым метром», чтобы в случае нужды пользоваться им для измерения.
Полезно помнить, что у большинства людей расстояние между концами расставленных рук равно росту – правило, подмеченное гениальным художником и ученым Леонардо да Винчи. Оно позволяет пользоваться нашими «живыми метрами», ведь свой рост знают почти все.
Давайте измерим себя.
Для обмеривания мелких расстояний следует помнить длину своей «четверти», т.е. расстояния между концами расставленных большого пальца и мизинца.
Далее полезно знать длину своего указательного пальца: от основания среднего пальца и от основания большого.
Должно быть известно вам наибольшее расстояние между концами указательного и среднего пальцев. Надо, наконец, знать и ширину своих пальцев.
Вооружившись всеми этими сведениями, вы сможете довольно удовлетворительно выполнять разнообразные измерения буквально голыми руками, даже в темноте.
Измерьте все перечисленные расстояния и запишите в тетрадь.
8. «Не верь глазам своим. » Геометрические иллюзии.
Одна семиклассница делилась со своей подругой-шестиклассницей впечатлениями об уроках геометрии: «Вот чудеса, пришла учительница в класс, нарисовала на доске два равных треугольника, а потом целый урок доказывала нам, что они равны. Никак не пойму: зачем это нужно? Ведь, что фигуры равны, это и так видно». «Чего же тут рассуждать,» – думают многие семиклассники, начиная изучать геометрию. «Посмотришь на чертеж, и сразу видно, что доказывать ничего не надо, всё и так видно, что доказывать ничего не надо, всё верно. Глаз не обманет».
Сравните длины отрезков:
А вот два четырехугольника, в них противоположные вершины соединены отрезками.
Сравните длины этих отрезков.
Установите – прямые, кривые, параллельные ли линии на чертежах?
Мы уже на прошлом уроке сравнивали такие отрезки (иллюзия Мюллера-Лайера):
— Как это называлось?
— Можно ли решить задачу на основании построенного чертежа?
— Не могут ли наши глаза обманывать нас?
9. Объяснение иллюзий.
Однажды известный математик пытался объяснить своему знакомому поэту, что такое пространство. Тот долго его слушал, а в конце заметил: «Это все не так. Я знаю, что пространство голубое и по нему летают птицы!» К сожалению математики смотрят на пространство более прозаично.
Геометрия изучает форму и взаимное расположение фигур (в пространстве – стереометрия, на плоскости – планиметрия).
С давних пор люди пытались объемные тела изобразить на плоскости так, чтобы их сразу можно было отличить от плоских, чтобы чувствовалась глубина пространства. Была разработана научная теория перспективы, позволяющая «обмануть» зрение.
Рассмотрите, как Вазарели с помощью изгибов линий удалось передать вмятины, выпуклости, капли на плоском листе.
Иллюзии рассматривают не только геометры, ими занимаются и физики, и психологи, и художники.
Иштван Орос. Венгерский художник родился в 1951 году. Обучался в Будапеште в Университете Искусств и Дизайна. После окончания обучения в 1975 стал работать в театре художником и участвовал в создании мультипликационных фильмов. Позже стал писать плакаты. В своем творчестве любит использовать иллюзии и визуальные парадоксы.
Жос де Мей (Jos de Mey). Фламандский художник родился в 1928 году. Обучался в Королевской Академии Искусств в Генте (Бельгия). Около 39 лет преподавал, а после 1968 основным его занятием стало рисование. На многих его работах можно увидеть сову как символ двойственности (по-голландски «сова» является символом теоретических знаний, а также образом глупого человека).
Мы воспринимаем окружающее нас как данность: солнечный луч, играющий бликами на поверхности воды, переливы красок осеннего леса, улыбку ребенка. Мы не сомневаемся, что реальный мир именно таков, каким мы его видим. Но так ли это на самом деле? Почему иногда зрение нас подводит? Как мозг человека интерпретирует воспринимаемые объекты?
Иллюзии – это искаженное, неадекватное отражение свойств воспринимаемого объекта. В переводе с латыни слово «иллюзия» означает «ошибка, заблуждение».
На иллюзиях Мюллера-Лайера и Понцо поробуем разобраться. Было предложено много теорий, объясняющих подобные искажения. Одна из более интересных гипотез предполагает, что человек накладывает обе картинки (отрезки) как плоские изображения в перспективе. Стрелочки на концах отрезков, а также схождение косых лучей в одной точке создают признаки перспективы, и человеку кажется, что отрезки расположены на разной глубине относительно наблюдателя.
Учитывая это, зрительная система вынуждена сделать вывод, что они разного размера. Те, которые кажутся удаленными, воспринимаются большими по размеру (вспомните картину В.Вазарели). Косые линии, сходящиеся в одной точке, ассоциируются либо с длинным шоссе, ж/дорожным полотном, на котором лежат два предмета. Зрительные шаблоны, сформированные таким «прямоугольным окружением, и заставляют нас ошибаться при взгляде на рисунки.
Позже мы рассмотрим и те картинки невозможного мира, которые вы уже видели ранее.
— Смогла я хоть немного заставить вас сомневаться в виденном?
Русская поговорка «Лучше один раз увидеть. », как раз и дает возможность осуществляться зрительным иллюзиям.
Иллюзии – результат работы зрительной системы, некий тест. Очень часто люди видят то, что они хотят увидеть. Ищите иллюзии вокруг, и вы больше узнаете о себе.
— Определите самое важное, что вы взяли для себя с урока.
10. Домашняя работа. Выставление оценок.
Вспомните пословицы, поговорки, в которых фигурируют меры длины.
Найти еще единицы измерения длины, которые не были перечислены на уроке.
Придумать и нарисовать картинку в стиле Вазарели.
Конечно, в этой разработке представлено лишь небольшое количество рисунков урока, в последующем далее списке литературы можно подобрать еще огромное количество иллюстративного материала к уроку.
Геометрия. 7 класс
Конспект урока
Перечень рассматриваемых вопросов:
Геометрия – это наука, занимающаяся изучением геометрических фигур и отношений между ними.
Отрезок – это часть прямой, ограниченная точками, вместе с этими точками.
Концы отрезка – это точки, ограничивающие отрезок.
Теоретический материал для самостоятельного изучения.
«Геометрия – неотъемлемая часть мировой сокровищницы человеческой мысли», – однажды сказал российский математик Игорь Фёдорович Шарыгин.
С этих слов мы и начнём изучать новый раздел математики, который называется геометрия.
Геометрия – одна из древнейших наук, которая возникла из потребностей человека. Её название состоит из двух древнегреческих слов: гео – земля и метрео – измеряю, получается: «землю измеряю». Действительно, слово «геометрия» связано с измерениями, как на земельных участках, так и при строительстве зданий. Многие факты добывались опытным путем, поэтому геометрия не являлась точной наукой во времена своего зарождения.
Геометрические сведения стали доказываться только благодаря древнегреческому учёному Фалесу, который жил в VI веке до нашей эры.
Спустя некоторое время, уже в III веке до нашей эры, другой греческий учёный Евклид написал «Начала». Эта книга стала основой изучения геометрии на долгое время, а наука в честь учёного была названа евклидовой геометрией.
Сегодня геометрия – это наука, занимающаяся изучением геометрических фигур и отношений между ними.
В школе изучается два курса геометрии – планиметрия, в ней рассматриваются свойства фигур на плоскости, и стереометрия, в ней рассматриваются свойства фигур в пространстве.
В каждой науке есть свои термины, понятия, геометрия не исключение. В геометрии есть основные положения, которые принимаются в качестве исходных и носят название аксиом и основные понятия, определение которым не даётся, например, точка и прямая, но их свойства выражены в аксиомах. Это всё является фундаментом геометрии, на котором строятся другие понятия и доказываются теоремы.
Рассмотрим некоторые из аксиом.
1. Аксиомы принадлежности.
Какова бы ни была прямая, существуют точки, принадлежащие ей и не принадлежащие ей.
2. Аксиомы расположения.
Из трех точек на прямой одна и только одна лежит между двумя другими.
3. Аксиомы измерения.
Каждый отрезок имеет определенную длину, большую нуля. Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.
В целом аксиомы разделены на 5 групп, 3 из которых, частично, представлены вашему вниманию.
В 7 классе вы будете изучать планиметрию. Давайте перечислим некоторые понятия из этого раздела геометрии. Поговорим о точках, прямых, отрезках, вспомним, как они обозначаются.
Обычно прямую обозначают малой латинской буквой (например, a), а точки большими латинскими буквами, например, A.
Если на прямой отметить точки, например, A и B, то прямую в можно обозначить двумя заглавными буквами AB или BA.
Часть прямой, ограниченной точками, включая эти точки, называют отрезком. В нашем случае получаем отрезок AB или BA.
Точки, ограничивающие отрезок, называются концами отрезка. В нашем случае концами отрезка являются точки A и B.
Варианты взаимного расположения точек и прямой: точки могут лежать на прямой или не лежать на ней.
Например, точки A и B лежат на прямой a, точки C и D не лежат на прямой a. При этом в записи используют следующее обозначение:
Это можно прочитать таким образом: «точка A и B принадлежат прямой a (ϵ – знак принадлежности), также точки C и D не принадлежат прямой a (перечёркнутый знак принадлежности)».
При этом через точки А и В нельзя провести прямую, не совпадающую с прямой а, из этого делаем вывод, что через любые две точки можно провести только одну прямую.
Рассмотрим, как располагаются прямые на плоскости.
Прямые могут иметь только одну общую точку, тогда говорят, что прямые пересекаются или не иметь общих точек, тогда говорят, что прямые не пересекаются.
прямые пересекаются – прямые не пересекаются
Решим задачу. Построим с помощью линейки отрезок длиннее, чем она сама. Приём, который мы будем использовать, называется провешиванием прямой.
Рассмотрим, в чём он заключается. Для этого приложим к листу бумаги линейку и отметим три точки А, В, С, при этом, точка С пусть лежит между точками А и В. Далее передвинем линейку так, чтобы её конец оказался около точки С, отметим точку D. Все построенные точки А, В, С, D лежат на одной прямой. Теперь проведём отрезок АВ, потом отрезок ВD, в результате получим отрезок АD длиннее, чем линейка.
Для построения на местности отмечают две точки, например, А и В, ставят в них шесты (вехи), третий шест ставят в точку С так, чтобы её закрывали уже ранее поставленные шесты.
Так можно прокладывать линии высоковольтных передач, трассы и т. д.
Разбор заданий тренировочного модуля.
1. Сколько отрезков образуется при пересечении прямых на рисунке?
Посмотрите на рисунок. На нём изображены 4 пересекающиеся прямые, точки пересечения разбивают прямые на отрезки: прямая с разбивается на 3 отрезка АЕ, АВ, ЕВ. Аналогично все прямые разбиваются на 3 отрезка. В результате получаем, что каждая из четырёх прямых, разбивается точками пересечения на 3 отрезка, значит: 4 · 3 = 12
2. Выберите правильные варианты ответа. С чем пересекается прямая m?
Решение: при выполнении задания, нужно помнить, что прямая бесконечно продолжается в обе стороны, а отрезок ограничен точками, поэтому, если продолжить прямую m и n, то становится понятно, что они пересекутся между собой. Кроме того, прямая m пересечётся и с отрезком АВ. Следовательно, получается 2 ответа: прямая m пересекается с прямой n и отрезком АВ.
Ответ: прямая m пересекается с прямой n; прямая m пересекается с отрезком АВ.