Что такое длина и ширина прямоугольника в математике
Длина прямоугольника – формула, примеры как найти
В этой статье мы поговорим о длине прямоугольника. Как определить, какая из сторон является длиной и зачем их разделять. Разберем три способа нахождения длины прямоугольника и решим небольшую задачу.
Что такое длина прямоугольника
Довольно часто люди путают местами длину и ширину прямоугольника, как правило, это не критично, но в результате значительно уменьшается наглядность, а от этого страдает качество решения.
Прямоугольник это частный случай параллелограмма. Параллелограмм, каждый угол которого равен 90 градусам, называется прямоугольником. Для наглядного изображения лучше будет, если нижней опорой прямоугольника будет служить длинна. Так сложилось, что такой рисунок больше всего напоминает рисунки в учебнике, а потому ученику будет проще разобраться в теме.
Рис. 1. Изображение прямоугольника
Три способа найти длину прямоугольника
Если разделить фигуру на две части диагональю, то можно заметить, что прямоугольник поделится ею на два прямоугольных треугольника. Из этого разделения и вытекают все формулы длины прямоугольника.
Через теорему Пифагора
Если известна длина диагонали ( обозначим ее буквой d) и ширина прямоугольника (примем значение за букву a). Тогда корень квадратный из разности квадратов диагонали и ширины будет равен длине прямоугольника.
Чтобы было понятнее, напишем решение в виде нескольких формул.
Согласно теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов. Гипотенуза это сторона, противоположная прямому углу, две другие стороны зовутся катетами. В нашем случае гипотенуза это диагональ.
Для того, чтобы определить значение b, нужно взять корень квадратный из обеих сторон получившегося выражения: b=(d2-a2)(-1)
В случае необходимости, можно поменять местами а и b, тогда получится формула ширины.
Через площадь
Рассмотрим еще один способ найти длину прямоугольника. Через площадь.Площадь прямоугольника равняется произведению длины на ширину. То есть, используя уже знакомые обозначения S=a*b. Выразим из этой формулы значение длины: b=S/b.
Так же, как и в первом методе, можно поменять местами а и b, чтобы получить формулу для ширины: a=S/b.
Тригонометрическая функция
Один из самых быстрых, но при этом немного сложных способов нахождения длины – воспользоваться тригонометрической функцией.
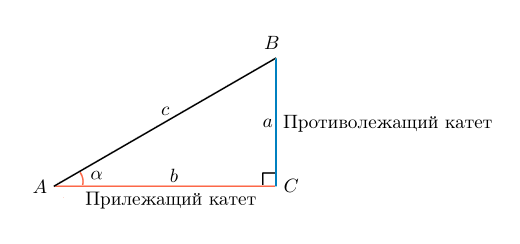
Если имеется прямоугольный треугольник, то соответственно имеются отношения, известные как синус и косинус.
Выберем угол между длинной и диагональю. Обозначим его α. Тогда sin α катета, противоположного углу α к гипотенузе: Sin α = a/d
Рис. 2. Угол альфа на половине прямоугольника
Значение синуса любого угла можно найти в таблицах Брадиса. Для удобства можно воспользоваться онлайн-версией, которая найдет значение отношения автоматически.
Но в формуле нет значения b, которое соответствует длине, а значит воспользуемся основным тригонометрическим тождеством.Косинус это отношение стороны, прилежащей к углу, к гипотенузе: cos a=b/d
Значит можно найти длину, умножив косинус на гипотенузу: b=cos α*d
Задача
Воспользуемся теоремой Пифагора и найдем b. Длина равна корню квадратному из разности квадрата диагонали и квадрата ширины.
Корень квадратный из 16 равен 4.
Рис. 3. Решение задачи
Что мы узнали?
Мы рассмотрели, как правильно изображать прямоугольник для большей наглядности, рассмотрели как можно найти длину при различных условиях задачи и решили задачу средней сложности на нахождение длины прямоугольника через теорему Пифагора.
Что такое прямоугольник: определение, свойства, признаки, формулы
В данной публикации мы рассмотрим определение, свойства и признаки одной из основных геометрических фигур – прямоугольника. Также приведем формулы, с помощью которых можно найти его площадь и периметр.
Определение прямоугольника
Прямоугольник – это четырехугольник, у которого все углы равны 90° (т.е. являются прямыми).
∠ABC = ∠BCD = ∠BAD = ADC = 90°
Прямоугольник состоит из:
Сам прямоугольник обычно записывается путем перечисления его вершин, например, ABCD в нашем случае.
Примечание: Прямоугольник является разновидностью параллелограмма.
Свойства прямоугольника
Свойство 1
Противоположные стороны прямоугольника попарно параллельны и равны.
Свойство 2
Длина и ширина прямоугольника одновременно являются его высотами, т.к. они взаимно перпендикулярны.
Свойство 3
Если соединить середины сторон прямоугольника, то получится ромб.
Свойство 4
Квадрат диагонали (d) прямоугольника равняется сумме квадратов его смежных сторон.
d 2 = a 2 + b 2
Это следует из теоремы Пифагора, которую можно применить к любому из прямоугольных треугольников, которые образуются в результате деления диагональю прямоугольника.
Свойство 5
Диагонали прямоугольника равны, и в точке пересечения делятся пополам.
Свойство 6
Около любого прямоугольника можно описать окружность, радиус (R) которой равен половине диагонали этого прямоугольника.
Следовательно, диаметр окружности равен полной длине диагонали прямоугольника.
Признаки прямоугольника
Параллелограмм является прямоугольником, если верно одно из следующих утверждений:
Формулы
1. Площадь прямоугольника (S):
2. Периметр прямоугольника (P):
Длина прямоугольника

Всего получено оценок: 79.
Всего получено оценок: 79.
В этой статье мы поговорим о длине прямоугольника. Как определить, какая из сторон является длиной и зачем их разделять. Разберем три способа нахождения длины прямоугольника и решим небольшую задачу.
Что такое длина прямоугольника
Довольно часто люди путают местами длину и ширину прямоугольника, как правило, это не критично, но в результате значительно уменьшается наглядность, а от этого страдает качество решения.
Прямоугольник это частный случай параллелограмма. Параллелограмм, каждый угол которого равен 90 градусам, называется прямоугольником. Для наглядного изображения лучше будет, если нижней опорой прямоугольника будет служить длина. Так сложилось, что такой рисунок больше всего напоминает рисунки в учебнике, а потому ученику будет проще разобраться в теме.
Три способа найти длину прямоугольника
Если разделить фигуру на две части диагональю, то можно заметить, что прямоугольник поделится ею на два прямоугольных треугольника. Из этого разделения и вытекают все формулы длины прямоугольника.
Через теорему Пифагора
Если известна длина диагонали (обозначим ее буквой d) и длина прямоугольника (примем значение за букву a). Тогда корень квадратный из разности квадратов диагонали и длины будет равен ширине прямоугольника.
Чтобы было понятнее, напишем решение в виде нескольких формул.
Согласно теореме Пифагора – квадрат гипотенузы равен сумме квадратов катетов. Гипотенуза – это сторона, противоположная прямому углу, две другие стороны зовутся катетами. В нашем случае гипотенуза это диагональ.
В случае необходимости, можно поменять местами а и b, тогда получится формула длины.
Через площадь
Рассмотрим еще один способ найти длину прямоугольника – через площадь.Площадь прямоугольника равна произведению длины и ширины. То есть, используя уже знакомые обозначения S=a*b. Выразим из этой формулы значение ширины: b=S/b.
Так же, как и в первом методе, можно поменять местами а и b, чтобы получить формулу для длины: a=S/b.
Тригонометрическая функция
Один из самых быстрых, но при этом немного сложных способов нахождения длины – воспользоваться тригонометрической функцией.
Если имеется прямоугольный треугольник, то соответственно имеются отношения, известные как синус и косинус.
Выберем угол между длиной и диагональю. Обозначим его α. Тогда sin α равен отношению катета, противоположного углу α к гипотенузе: Sin α = a/c
Значение синуса любого угла можно найти в таблицах Брадиса или с помощью калькулятора. Для удобства можно воспользоваться онлайн-версией, которая найдет значение отношения автоматически.
Но в формуле нет значения b, которое соответствует длине, а, значит, воспользуемся основным тригонометрическим тождеством. Косинус – это отношение стороны, прилежащей к углу, к гипотенузе: cos a=b/c
Значит можно найти длину, умножив косинус на гипотенузу: b=cos α*c
Задача
Воспользуемся теоремой Пифагора и найдем b. Длина равна корню квадратному из разности квадрата диагонали и квадрата ширины.
Корень квадратный из 16 равен 4.
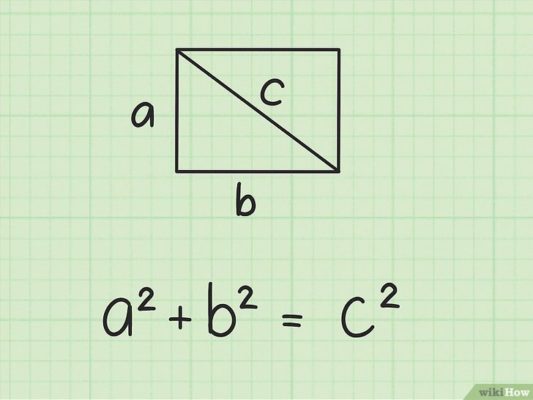
Что мы узнали?
Мы рассмотрели, как правильно изображать прямоугольник для большей наглядности, рассмотрели как можно найти длину или ширину при различных условиях задачи и решили задачу средней сложности на нахождение длины прямоугольника через теорему Пифагора.
Как определить длину и ширину прямоугольника?
Чтобы сначала вычислить длину и ширину прямоугольника, вычислите значение ширины ‘w’, используя формулу площади прямоугольника, а именно: ‘w = A / l’.
Впоследствии, что такое длина и ширина?
Длина относится к расстоянию между двумя концами объекта. Ширина относится к измерению ширины или ширины объекта.. Длина может быть измерена в геометрии, рассматривая самую большую сторону объекта. Ширину можно измерить в геометрии, рассматривая наименьшую сторону объекта.
Кроме того, длина прямоугольника в два раза больше ширины?
Длина прямоугольника в два раза больше Ширина. Количество квадратных единиц на его площади в четыре раза превышает количество единиц по периметру.
Во-вторых, какова формула периметра? Периметр, площадь и объем
Что такое ширина и высота?
Длина, ширина и высота равны измерения, позволяющие указывать объем геометрических тел. Длина (20 см) и ширина (10 см) соответствуют горизонтальному размеру. С другой стороны, высота (15 см) относится к вертикальному размеру.
Какая длина и ширина треугольника?
Каково уравнение периметра прямоугольника 96, когда длина прямоугольника вдвое больше ширины?
Как рассчитать площадь?
Как найти площадь и периметр?
Разделите периметр на 4: это дает вам длину одной стороны. Затем возведите эту длину в квадрат: это даст вам площадь. В этом примере 14 ÷ 4 = 3.5.
Какая формула для прямоугольника?
Формула площади прямоугольника
| Формула площади прямоугольника | |
|---|---|
| Периметр прямоугольника | P = 2 (l + b) |
| Площадь прямоугольника | А = l × b |
Что такое ДхШхВ?
Какой пример ширины?
Ширина определяется как степень ширины или измерение расстояния из стороны в сторону. Пример ширины 36 дюймов для ширины стола.
Какая длина треугольника?
Закон синусов гласит, что для всех углов треугольника отношение синуса этого угла к его противоположной стороне всегда будет одинаковым. Длина стороны c является 2.98. Закон косинусов гласит, что вы можете определить длину любой стороны треугольника, если вы знаете противоположный угол и длины двух других сторон.
Как определить ширину прямоугольной призмы?
Формула объема прямоугольной призмы:
Каков периметр прямоугольника?
Есть по периметру?
Какова площадь и периметр равностороннего треугольника?
Как найти периметр и площадь равностороннего треугольника? Площадь равностороннего треугольника √3 / 4 раза (сторона) 2 равностороннего треугольника и периметр равностороннего треугольника в 3 раза больше стороны равностороннего треугольника.
Как найти площадь четырехугольной формы?
Пример: четырехсторонняя фигура имеет две смежные стороны длиной 4 метра. Вы можете найти площадь этого квадрат, умножив его основание на высоту: 4 × 4 = 16 квадратных метров. Пример: обе диагонали квадрата равны 10 сантиметрам.
Как найти периметр и площадь прямоугольника?
Как найти периметр и площадь прямоугольника?
Какова площадь прямоугольного треугольника?
Что такое ширина, глубина и высота?
Например, размер прямоугольной комнаты на чертеже 14 футов 11 дюймов X 13 футов 10 дюймов соответствует размеру комнаты 14 футов, 11 дюймов в ширину на 13 футов, 10 дюймов в длину. Размеры выражаются как ширина, длина, высота или глубина в трехмерном пространстве.
Как найти длину, ширину и высоту?
Рассчитайте длину и обхват посылки вручную
Как рассчитать размеры?
Для расчета габаритной массы (DIM): умножьте длину, ширину и высоту пакета, используя самую длинную точку с каждой стороны. Затем разделите кубический размер упаковки в дюймах на делитель DIM, чтобы рассчитать размерный вес в фунтах.
Прямоугольник
Прямоугольник — параллелограмм, у которого все углы прямые (равны 90 градусам).
Примечание. В евклидовой геометрии для того, чтобы четырёхугольник был прямоугольником, достаточно, чтобы хотя бы три его угла были прямые. Четвёртый угол (в силу теоремы о сумме углов многоугольника) также будет равен 90°. В неевклидовой геометрии, где сумма углов четырёхугольника не равна 360° — прямоугольников не существует.
Содержание
Свойства
Площадь и стороны
Диагонали прямоугольника
Признаки
См. также
Планигон
Полезное
Смотреть что такое «Прямоугольник» в других словарях:
прямоугольник — прямоугольник … Орфографический словарь-справочник
прямоугольник — параллелограмм, четырехугольник, квадрат Словарь русских синонимов. прямоугольник сущ., кол во синонимов: 4 • квадрат (9) • … Словарь синонимов
«ПРЯМОУГОЛЬНИК» — термин, используемый в техническом анализе конъюнктуры финансовых рынков для обозначения движения цен, укладывающегося на графике в прямоугольник. Райзберг Б.А., Лозовский Л.Ш., Стародубцева Е.Б.. Современный экономический словарь. 2 е изд., испр … Экономический словарь
Прямоугольник — вид графика движения цены в виде треугольника, используемый в техническом анализе конъюнктуры финансовых рынков. Словарь бизнес терминов. Академик.ру. 2001 … Словарь бизнес-терминов
ПРЯМОУГОЛЬНИК — ПРЯМОУГОЛЬНИК, параллелограмм, все углы которого прямые … Современная энциклопедия
ПРЯМОУГОЛЬНИК — четырехугольник, у которого все углы прямые … Большой Энциклопедический словарь
ПРЯМОУГОЛЬНИК — ПРЯМОУГОЛЬНИК, четырехсторонняя геометрическая фигура (четырехугольник), внутренние углы которой являются прямыми, а противоположные стороны попарно параллельны и равны. Это особый случай ПАРАЛЛЕЛОГРАММА … Научно-технический энциклопедический словарь
ПРЯМОУГОЛЬНИК — ПРЯМОУГОЛЬНИК, прямоугольника, муж. (геом.). Четырехугольник, в котором все углы прямые. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова
ПРЯМОУГОЛЬНИК — ПРЯМОУГОЛЬНИК, а, муж. 1. Четырёхугольник, у к рого все углы прямые. 2. Название офицерского знака различия такой формы на петлицах в Красной Армии (с 1924 по 1943 г.). Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
«ПРЯМОУГОЛЬНИК» — вид графика движения цены в виде треугольника, используемый в техническом анализе конъюнктуры финансовых рынков. Словарь бизнес терминов. Академик.ру. 2001 … Словарь бизнес-терминов













