Что такое дизъюнкция в математике
Дизъюнкция
Логическая операция Дизъюнкция — бинарная операция над высказываниями, результатом которой является истинное высказывание в случаях, когда среди исходных высказываний есть хотя бы одно истинное. Дизъюнкция ложна, если оба исходных высказывания ложны.
Другие названия дизъюнкции — логическое сложение, логическое ИЛИ или просто ИЛИ.
Дизъюнкция изучается в информатике при рассмотрении раздела алгебра логики.
В естественных языках дизъюнкцию заменяют союзом «или«.
В языках программирования для дизъюнкции используют обозначение ‘ or ‘ или одинарной (двойной) вертикальной чертной ‘ | ‘ (либо ‘ || ‘) (например, x 5 или a>=10 || a ).
Как набрать знак дизъюнкцию на клавиатуре
Так как на клавиатуре нет знака дизъюнкции (∨), ее удобно набирать используя комбинацию символов обратный слэш и слэш \/.
Таблица истинности для дизъюнкции
Истинность дизъюнкции определяется ее таблицей истинности.
| A | B | A \/ B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Дизъюнкция и круги Эйлера
Результатом дизъюнкции является как область пересечения высказываний, там и области самих исходных высказываний.
Электрический аналог дизъюнкции
Представим, что выключатели A и B — это высказывания, причем 0 — выключатель разомкнут, 1 — выключатель замкнут. Лампа символизирует дизъюнкцию. Когда она не горит — 0, горящая лампа — 1. Тогда становится очевидным, что лампа будет гореть если хотя бы один (и оба сразу) выключатель будет замкнут, что полностью соотносится с таблицей истинности для дизъюнкции.
Конъюнкция и дизъюнкция — правила и примеры решения в математике
В информатике существует специальная дисциплина, рассматривающая логические операции отрицания, конъюнкции и дизъюнкции. В математике это направление называется булевой алгеброй и применяется для построения алгоритмов, проверяющих различные условия и соответствия. Специалисты в области информационных технологий рекомендуют перед практическим решением примеров получить теоретические знания.
Общие сведения
Булева алгебра — раздел математического анализа, изучающий истинность логических утверждений. Ее открыл Д. Буль в ХIХ веке. Алгебра логики получила практическое применение только в ХХ веке при проектировании различных элементов персонального компьютера. Дисциплина доказывает истинность или ложность тождеств логического типа математическим путем с применением специальных таблиц.
Следует отметить, что логическое тождество является определенной функцией, принимающей значения 0 или 1 в зависимости от ее элементов. В алгебре логики значения имеют следующие названия: 0 — ЛОЖЬ (FALSE) и 1 — ИСТИНА (TRUE).
Операторы сравнения
Следует отметить, что в этих примерах получается истинное значение, поскольку условие выполняется. Однако в информатике при построении алгоритмов используются методы ветвления. Они представляют собой такую конструкцию: ЕСЛИ (a>b), ТО a+b. ИНАЧЕ (a*b). Читается запись следующим образом: в том случае, когда значение а больше b, нужно сложить оба числа, а иначе (a Логические операции
Операции логического типа очень часто применяются при построении выражений, используемых в программировании. К ним относятся следующие:
Однако булева алгебра не ограничивается только ими, поскольку существуют и другие их производные. Для каждой из трех составляются определенные таблицы истинности, которые каждый раз необходимо строить для получения результата вычисления логических выражений. Специалисты рекомендуют отдельно на листе картона перечертить таблицы всех логических операций.
Функция конъюнкции
Конъюнкция — операция логического умножения, которая будет истинным при достоверности каждого выражения. Ее обозначение — символ конъюнктора «&». Записывается следующим образом: S&T, где S и T — логические тождества или конкретные значения. Операция имеет такие особенности: только при равенстве всех элементов 1 значение выражения является истинным, а в других случаях — ложью. Для проверки необходимо составить таблицу значений логического тождества:
| S | T | S&T |
| 0 | 0 | F |
| 0 | 1 | F |
| 1 | 0 | F |
| 1 | 1 | T |
Таблица 1. Значение функции в зависимости от логических переменных.
Из таблицы 1 видно, что выражение S&T принимает только TRUE при всех истинных значениях переменных. Если рассматривать алгебру, то можно провести аналогию между логическим и обыкновенным умножениями. Например, произведение двух чисел S*T, которые для удобства сравнения принимают значения 0 или 1.
Если сравнивать два результата, то они будут идентичны. Следовательно, для правильного построения таблицы для конъюнкции нужно руководствоваться аналогичной операцией умножения.
Информация о дизъюнкции
В булевой алгебре операция логического сложения называется дизъюнкцией. Обозначается она символом, который называется дизъюнктором (V или I). Логическое тождество, содержащее два элемента, имеет такой вид: SVT. Операция имеет только ложное значение при равенстве S и T нулю. Для нее нужно также строить специальную таблицу:
Таблица 2. Истинность операции дизъюнкции SVT.
Операция аналогична сложению в алгебре, хотя имеются некоторые отличия. Чтобы убедиться в этом, требуется выполнить определенное действие — построить специальную таблицу результатов для алгебраического сложения нулей и единиц.
Если рассмотреть результаты в последнем случае, то можно сделать вывод о схожести сложения и дизъюнкции. Однако в последней строке алгебраической суммы есть некоторое несоответствие — 2. Это показывает, какое переполнение разряда происходит в булевой алгебре. В последней происходит переход с одного разряда в другой.
Булево отрицание
В алгебре логики применяется также операция отрицания, которую также называют инверсией. Суть ее заключается в том, что при истинном значении выражения под знаком инверсии получается ложный результат, а при ложном — истина. Обозначается она символом инверсии «¬», а записывается в таком виде ¬(S). Для демонстрации операции необходимо ознакомиться с таблицей:
| Исходное выражение, S | Результат, ¬(S) |
| 0 | T |
| 1 | F |
Таблица 3. Истинность ¬(S).
Например, если необходимо указывать несколько тождеств логического вида, то при помощи отрицания можно использовать только одно. Для примера необходимо написать, что число не равно 0: (t 0). При использовании логического отрицания условие выглядит короче: t=!0.
Приоритеты вычислений
При решении выражений булевского типа, как и в алгебре, существуют определенные приоритеты. Каждая операция обладает определенным из них. Наибольшей степенью пользуется конъюнкция, средней — дизъюнкция. Наименьшим приоритетом обладает логическое отрицание. Однако эту особенность можно поменять при помощи группировки элементов в выражениях, которая производится скобками. С учетом этих особенностей алгоритм решения тождества имеет следующий вид:
Иногда бывают задачи, в которых следует упрощать выражение. Для этой цели следует знать некоторые особенности:
Этих правил достаточно для упрощения булевского выражения. Следует отметить, что перед построением булевской таблицы требуется с самого начала упростить исходное тождество.
Примеры решений
В первом простом примере требуется составить таблицу булевского типа для выражения S&(S|T)|T&S|¬(T&S).
Решать задание нужно по такому алгоритму:
Следующий пример будет сложнее, поскольку выражение ¬ < ¬[ ¬((S|0)&¬(T|S)& ¬(S&(T&S)) ]& ¬(S&S) >следует упростить, а затем составить таблицу. Задача решается по такой методике:
Следует отметить, что исходное логическое выражение необходимо на начальном этапе решения упростить, а затем строить таблицу. В этом возможно убедиться на основании приведенного примера, в котором сокращается одна переменная.
Таким образом, для решения выражения, содержащего логические операции конъюнкции, дизъюнкции и инверсии, необходимо его упростить, а затем разбить на простые элементы.
Логические операции и их свойства
Вы будете перенаправлены на Автор24
Конъюнкция или логическое умножение (в теории множеств – это пересечение)
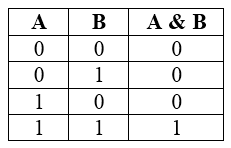
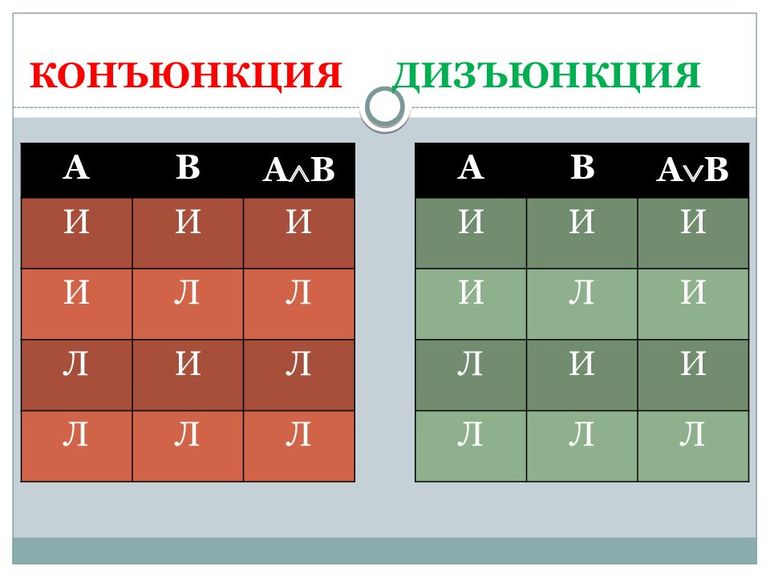
Конъюнкция является сложным логическим выражением, которое истинно в том и только том случае, когда оба простых выражения являются истинными. Такая ситуация возможно лишь в единственном случае, во всех остальных случаях конъюнкция ложна.
Таблица истинности для конъюнкции
Дизъюнкция или логическое сложение (в теории множеств это объединение)
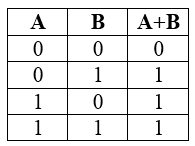
Дизъюнкция является сложным логическим выражением, которое истинно практически всегда, за исключением, когда все выражения ложны.
Таблица истинности для дизъюнкции
Готовые работы на аналогичную тему
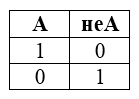
Отрицание, логическое отрицание или инверсия (в теории множеств это отрицание)
Таблица истинности для инверсии
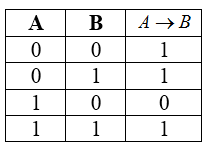
Импликация или логическое следование
Таблица истинности для импликации
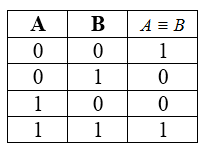
Эквивалентность или логическая равнозначность
Таблица истинности для эквивалентности
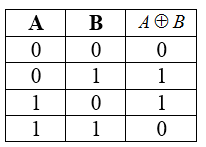
Строгая дизъюнкция или сложение по модулю 2 ( в теории множеств это объединение двух множеств без их пересечения)
Строгая дизъюнкция истинна, если значения аргументов не равны.
Таблица истинности для операции сложения по модулю два
Свойства строгой дизъюнкции:
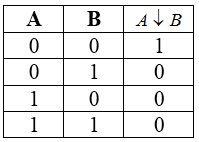
Стрелка Пирса
Таблица истинности для стрелки Пирса
Стрелка Пирса, как и конъюнкция, дизъюнкция, отрицание, образует базис для булевых функций двух переменных. При помощи стрелки Пирса, можно построить все остальные логические операции, например:
$X \downarrow X = ¬X$— отрицание
$(X \downarrow Y) \downarrow (X \downarrow Y) \equiv X \vee Y$ — дизъюнкция
$(X \downarrow X) \downarrow (Y \downarrow Y) \equiv X \wedge Y$ — конъюнкция
$((X \downarrow X) \downarrow Y) \downarrow ((X \downarrow X) \downarrow Y) = X \to Y$ — импликация
В электронике стрелка Пирса представлена в виде элемента, который носит название «операция 2ИЛИ-НЕ» (2-in NОR).
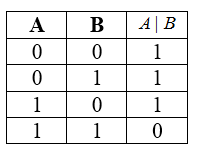
Штрих Шеффера
Булева функция двух переменных или бинарная логическая операция. Введена в рассмотрение Генри Шеффером в 1913 г.
Таблицей истинности для функции штрих Шеффера
Штрих Шеффера образует базис для всех булевых функций двух переменных. Применяя штрих Шеффера можно построить остальные операции, например,
$X \mid X = ¬X$ — отрицание
$(X \mid Y) \mid (X \mid Y) = (X \wedge Y)$ — конъюнкция
$(X \mid X) \mid (Y \mid Y) = X \vee Y$ — дизъюнкция
Для электроники это означает, что реализация схем возможна с использованием одного типового элемента (правда это дорогостоящий элемент).
Порядок выполнения логических операций в сложном логическом выражении
Для того чтобы изменить указанный порядок выполнения логических операций, необходимо использовать скобки.
Общие свойства
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата написания статьи: 24 03 2016
Что такое дизъюнкция в математике

2. Построение таблиц истинности и логических функций.
3. Законы логики и преобразование логических выражений.
Лабораторная работа № 3. Основы математической логики.

Исследования в алгебре логики тесно связаны с изучением высказываний (хотя высказывание — предмет изучения формальной логики). Высказывание — это языковое образование, в отношении которого имеет смысл говорить о его истинности или ложности (Аристотель).
Простым высказыванием называют повествовательное предложение, относительно которого имеет смысл говорить, истинно оно или ложно.
Считается, что каждое высказывание либо истинно, либо ложно и ни одно высказывание не может быть одновременно истинным и ложным.
Высказывания 1 и 3 являются истинными. Высказывание 2 – ложным , потому что число 27 составное 27=3*3*3.
Итак, отличительным признаком высказывания является свойство быть истинным или ложным, последние четыре предложения этим свойством не обладают.
С помощью высказываний устанавливаются свойства, взаимосвязи между объектами. Высказывание истинно, если оно адекватно отображает эту связь, в противном случае оно ложно.
Однако определение истинности высказывания далеко не простой вопрос. Например, высказывание «Число 1 +22 = 4294 967297 — простое», принадлежащее Ферма (1601-1665), долгое время считалось истинным, пока в 1732 году Эйлер (1707-1783) не доказал, что оно ложно. В целом, обоснование истинности или ложности простых высказываний решается вне алгебры логики. Например, истинность или ложность высказывания «Сумма углов треугольника равна 180°» устанавливается геометрией, причем в геометрии Евклида это высказывание является истинным, а в геометрии Лобачевского — ложным.
В булевой алгебре простым высказываниям ставятся в соответствие логические переменные, значение которых равно 1, если высказывание истинно, и 0, если высказывание ложно. Обозначаются логические переменные, большими буквами латинского алфавита.
Существуют разные варианты обозначения истинности и ложности логических переменных:
Сложные (составные) высказывания представляют собой набор простых высказываний (по крайней мере двух) связанных логическими операциями.
С помощью логических переменных и символов логических операций любое высказывание можно формализовать, то есть заменить логической формулой (логическим выражением).
Связки «НЕ», «И», «ИЛИ» заменяются логическими операциями инверсия, конъюнкция, дизъюнкция. Это основные логические операции, при помощи которых можно записать любое логическое выражение.
Введем перечисленные логические операции.
В алгебре множеств конъюнкции соответствует операция пересечения множеств, т.е. множеству получившемуся в результате умножения множеств А и В соответствует множество, состоящее из элементов, принадлежащих одновременно двум множествам.
Общие сведения
Булева алгебра — раздел математического анализа, изучающий истинность логических утверждений. Ее открыл Д. Буль в ХIХ веке. Алгебра логики получила практическое применение только в ХХ веке при проектировании различных элементов персонального компьютера. Дисциплина доказывает истинность или ложность тождеств логического типа математическим путем с применением специальных таблиц.
Следует отметить, что логическое тождество является определенной функцией, принимающей значения 0 или 1 в зависимости от ее элементов. В алгебре логики значения имеют следующие названия: 0 — ЛОЖЬ (FALSE) и 1 — ИСТИНА (TRUE).
Операторы сравнения
Например, если необходимо указывать несколько тождеств логического вида, то при помощи отрицания можно использовать только одно. Для примера необходимо написать, что число не равно 0: (t 0). При использовании логического отрицания условие выглядит короче: t=!0.
Приоритеты вычислений
При решении выражений булевского типа, как и в алгебре, существуют определенные приоритеты. Каждая операция обладает определенным из них. Наибольшей степенью пользуется конъюнкция, средней — дизъюнкция. Наименьшим приоритетом обладает логическое отрицание. Однако эту особенность можно поменять при помощи группировки элементов в выражениях, которая производится скобками. С учетом этих особенностей алгоритм решения тождества имеет следующий вид:
Иногда бывают задачи, в которых следует упрощать выражение. Для этой цели следует знать некоторые особенности:
Этих правил достаточно для упрощения булевского выражения. Следует отметить, что перед построением булевской таблицы требуется с самого начала упростить исходное тождество.
Примеры решений
В первом простом примере требуется составить таблицу булевского типа для выражения S&(S|T)|T&S|¬(T&S).
Решать задание нужно по такому алгоритму:
Следующий пример будет сложнее, поскольку выражение ¬ < ¬[ ¬((S|0)&¬(T|S)& ¬(S&(T&S)) ]& ¬(S&S) >следует упростить, а затем составить таблицу. Задача решается по такой методике:
Следует отметить, что исходное логическое выражение необходимо на начальном этапе решения упростить, а затем строить таблицу. В этом возможно убедиться на основании приведенного примера, в котором сокращается одна переменная.
Таким образом, для решения выражения, содержащего логические операции конъюнкции, дизъюнкции и инверсии, необходимо его упростить, а затем разбить на простые элементы.