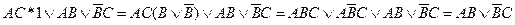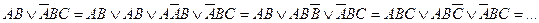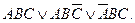Что такое дизъюнктивная форма
Дизъюнктивная нормальная форма
Оглавление
определение
Объяснение
Пример: A OR B OR C OR D; A∨B∨C∨D
Отдельные элементы ссылки ИЛИ (A, B, C, D) могут быть более сложными выражениями, которые могут также содержать одну или несколько ссылок И ( соединение ).
как формальное обозначение:
По договоренности скобки и символы (операторы) для ссылки И не записываются.
Оператор НЕ может также присутствовать в таких выражениях:
А. ¯ Б. ¯ С. ¯ ∨ А. ¯ Б. С. ¯ ∨ А. Б. С. ¯ ∨ А. ¯ Б. ¯ С. ∨ А. ¯ Б. С. ∨ А. Б. С. <\ displaystyle <\ bar > <\ bar > <\ bar
В дополнение к вышеупомянутому требованию о том, что логическое выражение на верхнем уровне состоит исключительно из связей ИЛИ (уровень ИЛИ), на нижних уровнях в квадратных скобках не должно быть дополнительных ссылок ИЛИ. Разрешены только два уровня: верхний уровень ссылок ИЛИ (уровень ИЛИ) и нижний уровень ссылок И (уровень И). Нет более глубокого вложения. Только отрицание может использоваться для элементов уровня И.
образование
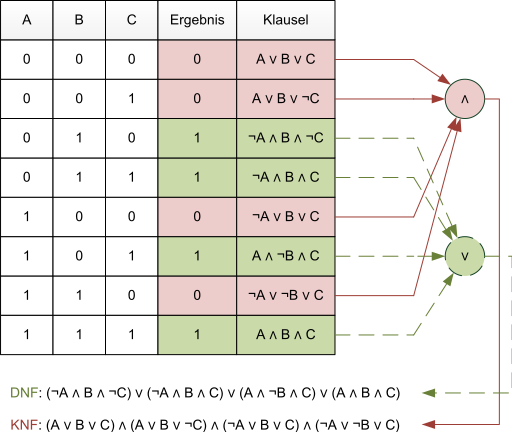
Пример формирования ДНФ
Таблица истинности для этой функции имеет следующий вид:
Функция, представленная в DNF
y знак равно Икс 2 ¯ Икс 1 Икс 0 ¯ ∨ Икс 2 ¯ Икс 1 Икс 0 ∨ Икс 2 Икс 1 ¯ Икс 0 ∨ Икс 2 Икс 1 Икс 0 <\ displaystyle y = <\ bar
также может быть представлено как логическое выражение в квадратных скобках:
е знак равно ( ( Икс 2 ¯ ) ∧ Икс 1 ) ∨ ( Икс 2 ∧ Икс 0 ) <\ Displaystyle е = ((<\ бар
е знак равно Икс 2 ¯ Икс 1 + Икс 2 Икс 0 <\ displaystyle e = <\ bar
Как и в математике, истинность термина продукта определяется путем умножения значений логических переменных. Если одна из задействованных переменных равна нулю, значение всего термина продукта равно нулю; член продукта принимает значение один тогда и только тогда, когда все переменные в нем имеют значение один.
CPLD используют термины продукта, связанные дизъюнктивно (ИЛИ), для определения своей функции.
Каноническая дизъюнктивная нормальная форма
В KDNF те назначения переменных, для которых функция принимает значение 1, выражаются minter terms.
Ортогональная дизъюнктивная нормальная форма
Более нормальные формы
Дизъюнктивная минимальная форма
Для всякой логической формулы с помощью тождественных преобразований можно построить бесконечно много равносильных ей формул. В алгебре логики одной из основных задач является поиск канонических форм (т. е. формул, построенных по единому правилу, канону).
Если логическая функция выражена через дизъюнкцию, конъюнкцию и отрицание переменных, то такая форма представления называется нормальной.
Среди нормальных форм выделяются совершенные нормальные формы (такие формы, в которых функции записываются единственным образом).
Совершенная дизъюнктивная нормальная форма (СДНФ)
Определение. Формулу называют элементарной конъюнкцией, если она образованна конъюнкцией некоторого числа переменных или их отрицаний.
Определение. Формула называтся дизъюнктивной нормальной формой (ДНФ), если она является дизъюнкцией неповторяющихся элементарных конъюнкций.
Определение. Логическая формула от k переменных называется совершенной дизъюнктивной нормальной формой (СДНФ), если:
1) формула является ДНФ, в которой каждая элементарная конъюнкция есть конъюнкция k переменных х1, х2, …, хk, причем на i-м месте этой конъюнкции стоит либо переменная хi, либо ее отрицание;
2) все элементарные конъюнкции в такой ДНФ попарно различны.
Совершенная конъюнктивная нормальная форма (СКНФ)
Определение. Формулу называют элементарной дизъюнкцией, если она образована дизъюнкцией некоторого числа переменных или их отрицаний.
Определение. Формула называется конъюнктивной нормальной формой (КНФ), если она является конъюнкцией неповторяющихся элементарных дизъюнкций.
Определение. Логическая формула от k переменных называется совершенной конъюнктивной нормальной формой (КДНФ), если:
1) формула является КНФ, в которой каждая элементарная дизъюнкция есть дизъюнкция k переменных х1, х2, …, хk, причем на i-м месте этой дизъюнкции стоит либо переменная хi, либо ее отрицание;
2) все элементарные дизъюнкции в такой КНФ попарно различны.
Алгоритм построения СДНФ по таблице истинности
Алгоритм построения СКНФ по таблице истинности
Пример: Дана таблица истинности логической функции от трех переменных. Построить логическую формулу, реализующую эту функцию.
| x | y | z | F (x, y, z) |
|---|---|---|---|
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Т.к. на большинстве строк таблицы истинности значение функции равно 1, то построим СКНФ. В результате получим следующую логическую формулу:
F = (¬ x ∨ y ∨ z) ∧ (¬ x ∨ y ∨ ¬ z)
Проверим полученную формулу. Для этого построим таблицу истинности функции.
| x | y | z | ¬ x | ¬ x ∨ y ∨ z | ¬ z | ¬ x ∨ y ∨ ¬ z | F (x, y, z) |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 |
Сравнив исходную таблицу истинности и построенную для логической формулы, заметим, что столбцы значений функции совпадают. Значит, логическая функция построена верно.
Copyright © 2014-2021, Урок информатики
Все права защищены
Дизъюнктивные и конъюнктивные нормальные формы. Совершенные конъюнктивные и дизъюнктивные нормальные формы



Элементарной конъюнкцией называется конъюнкция, состоящая только из переменных или их отрицаний. Например: 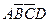
Дизъюнктивно-нормальной формой (ДНФ) называется дизъюнкция элементарных конъюнкций. Например: 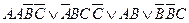
Если учесть, что нулевые конъюнкции можно опустить, а А*А=А, то приведенная ДНФ сведется к более простому виду: 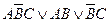
Дальнейшее упрощение получается с помощью законов поглощения: 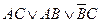
Покажем, что это действительно так:
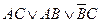
(по закону поглощения 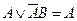
Мы доказали следующее правило поглощения:
Если ДНФ является трехчленом, зависящим от трех переменных, и если симметрия нарушена только по одной из переменных, то пропадает тот член дизъюнкции, который эту переменную не содержит.
1. 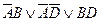
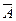
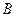
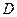
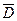
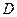
Поэтому, согласно нашему правилу, пропадает член, не содержащий букву 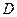
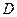
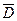
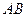
2. 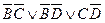
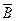
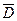
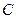
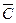
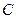
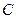
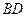
Минимальной мы назовемту ДНФ, которая имеет самую короткую запись.
Существует еще одно правило поглощения, которое тоже основано на соображениях симметрии:
Если ДНФ является трехчленом, зависящим от трех переменных, и если симметрия нарушена по двум из этих переменных, то данная ДНФ равносильна дизъюнкции, одним из членов которой является переменная, по которой симметрия не нарушена, а вторым членом служит тот член первоначальной ДНФ, который эту переменную не содержит.
Например: 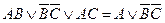

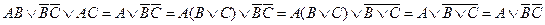
1. 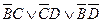
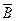
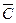
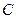
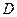
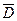
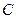
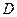
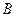
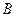
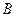
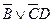
2. 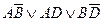
В этом трехчлене симметрия нарушена по 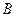
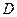
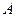
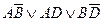
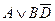
Для каждой формулы существует бесконечно много различных, но равносильных ей ДНФ. Если, например, найдена одна ДНФ, то путем повторения имеющихся элементарных конъюнкций, добавления нулевых конъюнкций, добавления поглощаемых конъюнкций можно построить бесконечно много новых, но равносильных ей ДНФ.
Например:
Среди всех этих ДНФ есть одна, которая отличаете однородностью и «совершенством» своей формы. Mы имеем в виду формулу:
Она так и называется: «совершенная дизъюнктивно-нормальная форма»(СДНФ).
Дадим точное определение:
СДНФ — это такая ДНФ, которая удовлетворяет следующим условиям:
1. Все элементарные конъюнкции различны.
2. Нет нулевых конъюнкций.
3. Ни одна из элементарных конъюнкций не содержит одинаковых членов.
4. Каждая элементарная конъюнкция содержит все переменные.
Чтобы получить СДНФ, надо сначала найти минимальную ДНФ. Тогда будут выполнены условия 1, 2, 3. Посли этого надо преобразовать эту минимальную ДНФ таким образом, чтобы было выполнено условие 4. Это делается следующим образом:
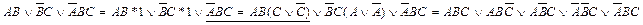
Элементарной дизъюнкцией называется дизъюнкция, состоящая только из переменных или их отрицаний. Например: 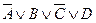
Конъюнктивной нормальной формой (КНФ) называется конъюнкция элементарных дизъюнкций. Например: 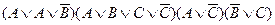
Если воспользоваться равносильностью 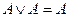
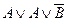
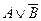
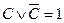
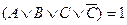
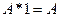
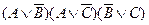
Но эта формула не является еще минимальной. Для КНФ тоже существуют правила поглощения, основанные на соображениях симметрии. Эти правила можно получить по закону двойственности из аналогичных правил, установленных для ДНФ.
Мы знаем, например, что: 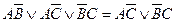
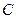
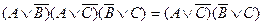
В то же время мы установили новое правило поглощения:
Если КНФ зависит от трех переменных и представляет собой конъюнкцию трех элементарных дизъюнкций и если симметрия нарушена только по одной из переменных, то поглощается та элементарная дизъюнкция, которая эту переменную не содержит.
Аналогичным образом можно получить и второе правило поглощения, основанное на соображениях симметрии. Мы уже знаем, что: 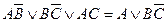
Запишем двойственную равносильность:
Сформулируем соответствующее правило поглощения:
Если КНФ зависит от трех переменных и представляет собой конъюнкцию трех элементарных дизъюнкций и если симметрия нарушена по двум из этих переменных, то данная КНФ равносильна конъюнкции, одним из членов которой является переменная, по которой симметрия не нарушена, а вторым членом является тот член первоначальной КНФ, который эту переменную не содержит.
Чтобы найти минимальную КНФ, равносильную данной формуле, надо эту формулу сначала привести к виду ДНФ, затем надо разложить ее на «множители» и применить законы поглощения.
Рассмотрим конкретный пример:
Можно поступить и по-другому. Новый подход начнется с того момента, когда была получена формула 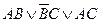
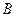
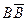
Что такое дизъюнктивная форма
Пусть имеем множество переменных X=
Определение. Элементарной конъюнкцией назовем конъюнкцию переменных множества X, в которую каждая переменная входит не более одного раза (с инверсией или без инверсии).
Определение. Число переменных, образующих элементарную конъюнкцию, назовем ее рангом.
Примеры. Ранги элементарных конъюнкций x1 x 3x4 и 1 равны трем и нулю. •
Определение. Полной конъюнкцией назовем элементарную конъюнкцию, состоящую из всех n переменных множества X, то есть конъюнкцию ранга n.
Определение. Две конъюнкции называются ортогональными по переменной xi, если эта переменная входит в одну конъюнкцию с инверсией, а в другую без инверсии.
Определение. Две конъюнкции называются смежными, если они ортогональны по одной и только одной переменной xi (принято также говорить »смежны по переменной xi»).
Пример. Конъюнкции x1x2 x 3 и x1x3 x 4 являются смежными по переменной x3 (ортогональны только по x3). •
Определение. Две конъюнкции называются соседними, если они ортогональны по одной и только одной переменной xi и совпадают по остальным (принято также говорить »соседние по переменной xi»).
Пример. Конъюнкции x1x2 x 3 и x1x2 x3 являются соседними по переменной x3 (ортогональны только по x3 и совпадают по x1 и x2). •
Законы склеивания и обобщенного склеивания применяются, как нетрудно видеть, к соседним и смежным конъюнкциям соответственно. Поэтому их также называют законами склеивания соседних конъюнкций и обобщенного склеивания смежных конъюкнций и иногда добавляют, по какой именно переменной.
Примеры. Конъюнкции x1x2 x 3 и x1x2 x3 являются соседними по переменной x3, следовательно, к ним применим закон склеивания соседних конъюнкций по x3:
Конъюнкции x1x2 x 3 и x1x3 x 4 являются смежными по переменной x3, следовательно, к ним применим закон обобщенного склеивания смежных конъюнкций по x3:
Определение. Дизъюнктивной нормальной формой(ДНФ) булевой функции f(x1, …, xn) назовем дизъюнкцию различных элементарных конъюнкций, задающую функцию f(x1, …, xn).
Пример. x1 x 2 

Определение. Длиной ДНФ назовем число ее конъюнкций, а рангом ДНФ – сумму рангов конъюнкций.
Пример. Длина ДНФ из предыдущего примера равна трем, а ранг – восьми. •
Будем применять обозначение ДНФf, если захотим отметить, что ДНФ представляет булеву функцию f(x1, …, xn).
Очевидно, что совершенная ДНФ является частным случаем ДНФ, все конъюнкции которой полные. Любая ДНФ может быть преобразована в совершенную ДНФ с использованием основных равносильностей – законов склеивания и поглощения конъюнкций.