Что такое дискретные числа
Что такое дискретность (дискретная математика, сигнал, величины, видеокарты, а так же дискретность в биологии)
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Знать все обо всем попросту невозможно. Человек на протяжении всей жизни стремится познать себя и окружающую его действительность.
Вот и сегодня мы продолжим свой познавательный процесс, поговорим о новом (для многих) термине – « дискретность», и о сферах, где он применяется.
Дискретность – это …
Наш мир непрерывен, мы живем в постоянно меняющемся времени и пространстве. Наша жизнь тоже непрерывна до своего конечного момента. Согласитесь, невозможно сейчас жить, через час не жить, а потом вновь возродиться.
В противопоставлении непрерывности существует дискретность. В переводе с «вечно живого» латинского языка «дискретность» (discretus) обозначает прерывность, разделенность.
Дискре́тность (от лат. discretus — разделённый, прерывистый) — свойство, противопоставляемое непрерывности, прерывистость. Синонимы к слову дискретный: корпускулярный, отдельный, прерывистый, раздельный и т. п.
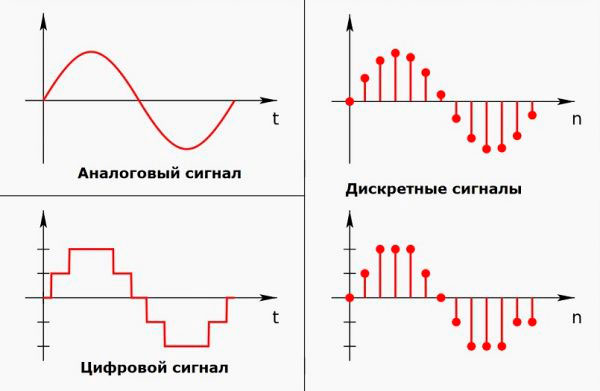
Например, линия непрерывна (на определенном промежутке), пунктир – прерывистая линия. Поэтому пунктир можно назвать дискретной линией. Проиллюстрирую понятие дискретности:
Дискретность можно толковать следующим образом:
Далее проанализируем особенности применения термина в различных областях.
Дискретная математика
Если коротко и простыми словами, то дискретная математика (ДМ)– это наука, которые изучает математические объекты, принимающие отдельные (дискретные) значения.
ДМ условно подразделяется на пять направлений:
Дискретная величина
Дискретность какой-либо величины подразумевает, что ее значения можно пронумеровать, измерить и посчитать.
Такими величинами оперирует, например, экономика. Различные экономические показатели фиксируют и рассчитывают с определенной периодичностью (например, раз в месяц, квартал, полугодие и т.д.). Таким образом, изменение показателей происходит не непрерывно во времени, а как бы «скачками» через установленные интервалы времени.
Дискретность в информатике
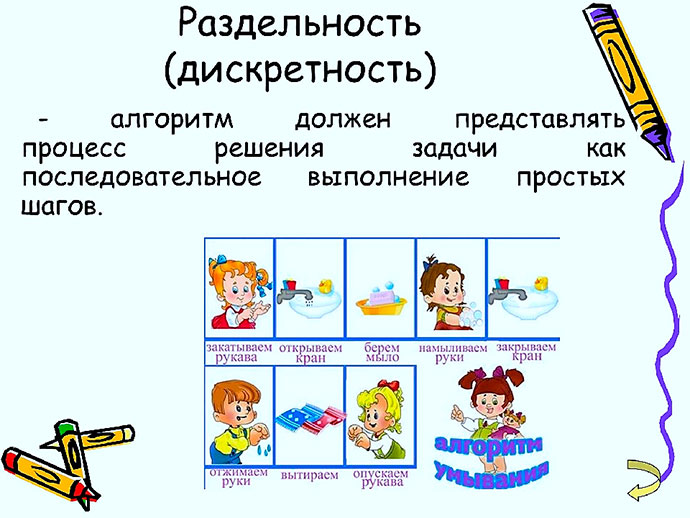
Программирование – это создание программ с использованием различных алгоритмов и языков программирования. Алгоритмы являются дискретными объектами, потому как представляют собой четкое последовательное выполнение ранее разработанных упрощенных шагов-действий (подпрограмм).
Только исполнение шага № 1 дает возможность выполнить шаг № 2 и т.д. Таким образом, этот процесс дискретен.
Как пример – алгоритм умывания (компьютерные программы создаются по тому же принципу):
Дискретная видеокарта
Видеокарта – один из важнейших элементов компьютера, отвечающий за визуализацию информации. Конструкция компа может быть оснащена либо интегрированной (встроенной) видеокартой, либо дискретной. Встроенная размещается в процессоре или на материнской плате, т.е. она неотделима от конкретного компьютера.
Дискретная видеокарта выполнена на отдельной плате, снабжена индивидуальным графическим процессором и памятью. Поэтому она более производительна, чем интегрированная.
Часто в компьютерах применяются видеокарты обоих видов, что позволяет пользователю при необходимости переключаться с одной на другую.
Дискретность в биологии
Все биологические объекты состоят из отдельных (дискретных) «кирпичиков», которые в совокупности образуют единый организм. Например, скелет человека состоит из костей, кости –из костной ткани, она, в свою очередь – из клеток.
Автор статьи: Елена Копейкина
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Эта статья относится к рубрикам:
Комментарии и отзывы (1)
Благодарю за дискретное изложение материала
Дискретные и непрерывные данные – в чем разница?
Оглавление
Для такого простого слова «данные» – довольно сложная тема. Например, «любовь» или «новости». Есть структурированные и неструктурированные данные. Тогда у вас есть качественные и количественные данные.
Теперь мы хотели бы изучить еще два типа данных – дискретный и непрерывный – и помочь вам понять разницу. (Тогда ваша организация может использовать статистическое программное обеспечение, чтобы получить представление о обоих типах.)
Чем больше вы понимаете об этих уникальных типах данных, тем больше вы сможете определить возможности, в которых каждый из них может пригодиться. Затем вы можете использовать эту информацию, чтобы принести пользу своему бренду, независимо от того, являетесь ли вы специалистом по обработке данных, аналитиком данных, инженером по обработке данных – или просто поклонником цифр.
Дискретные и непрерывные данные
В чем разница между дискретными и непрерывными данными?
Когда вы соберете набор круглых определенных чисел, они окажутся на своем месте на графике, похожем на те, что показаны слева. Дискретные данные относятся к отдельным счетным предметам.
Когда вы измеряете определенный поток данных со сложным диапазоном результатов, эти результаты будут обозначены линией в виде диапазона данных (см. Графики справа). Непрерывные данные относятся к изменениям с течением времени, включая концепции, которые не просто подсчитать, но требуют подробных измерений.
Подождите, пока мы немного раскроем эти термины для лучшего понимания.
Что такое дискретные данные?
Некоторые синонимы слова «дискретный» включают: разъединенный, отдельный и отдельный. Их можно легко применить к идее дискретных данных.
Мы собираем данные, чтобы найти взаимосвязи, тенденции и другие концепции. Например, если вы отслеживаете количество отжиманий, которые вы делаете каждый день в течение месяца, основной целью является оценка вашего прогресса и скорости улучшения.
С учетом сказанного, ваш дневной счет – это дискретное, изолированное число. Нет четкого диапазона того, сколько вы можете сделать за один день, поэтому отношения остаются неопределенными. Чем больше информации вы собираете с течением времени, тем больше идей вы можете сделать, например, что среднее количество отжиманий, которые вы делали на прошлой неделе, составляло 15 отжиманий в день, что на 5 отжиманий в день больше, чем неделей ранее. Между тем, сами числа отжиманий – это целые, круглые числа, которые нельзя разбить на более мелкие части.
Забавное практическое правило состоит в том, что во многих случаях дискретным данным может предшествовать «количество».
Примеры дискретных данных
Некоторые примеры дискретных данных, которые можно собрать:
Дискретные данные также могут быть качественными. Национальность, которую вы выбираете в форме, – это отдельные данные. Национальность каждого на вашей работе, если сгруппировать вместе с помощью программного обеспечения для работы с электронными таблицами, может быть ценной информацией при оценке вашей практики найма.
Национальная перепись состоит из дискретных данных, как качественных, так и количественных. Подсчет и сбор этой идентифицирующей информации углубляет наше понимание населения. Это помогает нам делать прогнозы о будущем, документируя историю. Это отличный пример силы дискретных данных.
Что такое непрерывные данные?
Непрерывные данные относятся к нефиксированному количеству возможных измерений между двумя реалистичными точками.
Эти числа не всегда чистые и аккуратные, как те, которые содержатся в дискретных данных, поскольку они обычно собираются на основе точных измерений. Со временем измерение определенного объекта позволяет нам создать определенный диапазон, в соответствии с которым мы можем разумно ожидать сбора большего количества данных.
Непрерывные данные – это все о точности. Переменные в этих наборах данных часто имеют десятичные точки, а число справа растянуто, насколько это возможно. Этот уровень детализации имеет первостепенное значение для ученых, врачей и производителей, и это лишь некоторые из них.
Примеры непрерывных данных
Некоторые примеры непрерывных данных включают:
Когда вы думаете об экспериментах или исследованиях, включающих постоянные измерения, они, вероятно, в некоторой степени связаны с непрерывными переменными. Если где-нибудь в таблице у вас есть число вроде «2,86290», это не то число, которое вы могли бы легко вычислить сами – подумайте об измерительных устройствах, таких как секундомеры, весы, термометры и тому подобное.
Задача с использованием этих инструментов, вероятно, применима к непрерывным данным. Например, если мы отслеживаем каждого бегуна на Олимпийских играх, время будет отображаться на графике вдоль соответствующей линии. Несмотря на то, что с годами наши спортсмены становятся быстрее и сильнее, никогда не должно быть выбросов, искажающих остальные данные. (Даже Усэйн Болт всего на пару секунд быстрее, чем историческое поле, если говорить об этом.)
На этой линии есть бесконечные возможности (например, 5,77 секунды, 5,772 секунды, 5,7699 секунды и т. Д.), Но каждое новое измерение будет постоянно находиться где-то в пределах диапазона.
Не каждый пример непрерывных данных будет аккуратно попадать в прямую линию, но со временем диапазон станет более очевидным, и вы можете сделать ставку на новые точки данных, застрявшие внутри этих параметров.
Основы дискретной математики
Привет, хабр. В преддверии старта базового курса «Математика для Data Science» делимся с вами переводом еще одного полезного материала.
Об этой статье
Эта статья содержит лишь малую часть информации по заявленной теме. Рассматривайте ее как вводный курс перед началом всестороннего изучения предмета. Надеюсь, вы найдете в ней полезную информацию. Знание дискретной математики помогает описывать объекты и задачи в информатике, особенно когда дело касается алгоритмов, языков программирования, баз данных и криптографии. В дальнейшем я планирую подробнее раскрыть темы, затронутые в этой статье. Приятного чтения!
ЧТО ТАКОЕ ДИСКРЕТНАЯ МАТЕМАТИКА?
Это область математики, изучающая объекты, которые могут принимать только уникальные отдельные значения.
Мы рассмотрим пять основных разделов в следующем порядке.
ЛОГИКА
Что такое логика?
Это наука о корректных рассуждениях. Мы будем использовать приемы идеализации и формализации. Неформальная логика изучает использование аргументов в естественном языке.
Формальная логика анализирует выводы с чисто формальным содержанием. Примерами формальной логики являются символическая логика и силлогистическая логика (о которой писал Аристотель).
Начнем с азов. Рассмотрим следующее высказывание на естественном языке:
«Если я голоден, я ем».
Пусть «голоден» будет посылкой A, а «ем» — следствием B. Попробуем формализовать:
A => B (то есть из A следует B)
NB. Посылка и следствие являются суждениями.
Логические выражения
Для нас важна форма, а НЕ содержание. Значение будет истинным, если оно соответствует форме.
Например, 10 4 — ИСТИНА.
Логические операции
Суждение P — это утверждение, которое может быть как истинным, так и ложным.
Обозначим истинное значение P единицей (1), а ложное значение P нулем (0).
Существует другое суждение; обозначим истинное значение Q единицей (1), а ложное значение Q нулем (0).
Рассмотрим логические операции с суждениями, значение которых истинно. Они могут сами образовывать истинные значения путем выполнения соответствующих операций над истинными значениями.
Статистические типы данных, используемые в машинном обучении
Sep 21, 2020 · 7 min read
Введение в статистику
Статистика — это наука об изучении данных. Знания в этой области позволяют использовать подходящие методы сбора и анализа данных, а также эффективно представлять результаты такого анализа. Статистика играет ключевую роль в научных открытиях, принятии решений и составлении прогнозов, основанных на данных. Она позволяет гораздо глубже разобраться в объекте исследования.
Чтобы стать успешным специалистом по теории и методам анализа данных, необходимо знать основы статистики. Математика и статистика — “строительные блоки” алгоритмов машинного обучения. Чтобы понимать, как и когда следует использовать различные алгоритмы, нужно знать, какие методы за ними стоят. Тут встаёт вопрос — что именно собой представляет статистика?
Ста т истика — это математическая наука о сборе, анализе, интерпретации и представлении данных.
Для чего изучать статистику?
Один из основных принципов науки о данных — получение выводов из их анализа. Статистика отлично для этого подходит. Она является разновидностью математики и использует формулы, но она отнюдь не обязательно покажется пугающей, даже если вам не приходилось сталкиваться с ней раньше.
Машинное обучение зародилось из статистики. Основой используемых в нём алгоритмов и моделей является так называемое статистическое обучение. Знание основ статистики крайне полезно вне зависимости от того, изучаете вы глубоко алгоритмы МО или просто хотите быть в курсе новейших исследований в этой сфере.
Введение в типы данных
Хорошее понимание разных типов данных (шкал измерений) — основное условие для проведения разведочного анализа данных (EDA), ведь для определённых типов данных можно использовать только ограниченный набор статистических измерений.
Чтобы решить, какой метод визуализации выбрать, также необходимо понимать, с какими данными вы имеете дело. Думайте о типах данных как о способе категоризации разновидностей переменных. Далее мы обсудим основные типы данных и рассмотрим примеры для каждого из них.
Данные:
2. Категориальные (выражены словами): цвет глаз, пол, группа крови, этническая принадлежность
Типы данных:
Качественные и количественные данные
Разделение данных на качественные и количественные — основополагающий принцип разделения данных на типы. Чтобы определить тип, нужно выяснить, можно ли объективно измерить исследуемую характеристику с помощью чисел.
1) Качественные данные
В информации представлены характеристики, которые не измеряются числами, в то время как сами наблюдения можно разделить на измеряемое количество групп. Информацию, хранящуюся в таком типе переменной, трудно измерить, а измерения могут быть субъективными. Вкус, цвет автомобиля, архитектурный стиль, семейное положение — всё это типы качественных данных. Аналитики также называют такие данные категориальными.
1.1) Номинальные данные
Номинальные значения выражают дискретные единицы и служат для обозначения переменных, которые не имеют количественного выражения. Номинальные данные не имеют порядка, поэтому при изменении порядка значений итоговый результат не меняется. Ниже представлено два примера номинальных признаков:
Методы визуализации: для визуализации номинальных данных можно использовать круговую или столбчатую диаграмму.
В науке о данных можно использовать прямое кодирование, чтобы преобразовать номинальные данные в числовое свойство.
1.2) Порядковые данные
Порядковые данные — это смесь числовых и категориальных данных. Данные можно разбить на категории, но числа, ассоциируемые с каждой категорией, имеют значение. К примеру, рейтинг ресторана от 0 (самый низкий) до 4 (самый высокий) звёзд — это пример порядковых данных. Порядковые данные часто обрабатываются как категориальные, когда при построении диаграмм и графиков данные разделяются на упорядоченные группы. Однако, в отличие от категориальных, числа в порядковых данных имеют математическое значение. Таким образом, порядковые данные — это почти то же самое, что и номинальные, с тем лишь отличием, что в номинальных порядок не имеет значения. Взгляните на пример ниже:
Порядковые шкалы обычно используются для измерения нечисловых свойств, таких как счастье, уровень удовлетворённости клиентов, успеваемость студентов в классе, уровень квалификации и т. д.
Такие данные можно обобщать с помощью частотности, пропорций, процентных долей, а визуализировать — с помощью круговых и столбчатых диаграмм. Кроме того, можно использовать процентиль, медиану, моду, межквартильный размах.
В дополнение к порядковым и номинальным есть особый тип категориальных данных — бинарные (двоичные).
Бинарные данные принимают только два значения — “да” или “нет”, что можно представить разными способами: “истина” и “ложь” или 1 и 0. Бинарные данные широко применяются в классификационных моделях машинного обучения. В качестве примеров бинарных переменных можно привести следующие ситуации: отменил человек подписку или нет, купил машину или нет.
2) Количественные данные
Информация записывается в виде чисел и представляет объективное измерение или подсчёт. Температура, вес, количество транзакций — вот примеры количественных данных. Аналитики также называют такие данные числовыми.
2.1) Дискретные данные
Дискретные количественные данные — это подсчёт случаев наличия характеристики, результата, предмета, деятельности. Эти измерения невозможно поделить на более мелкие части без потери смысла. Например, у семьи может быть 1 или 2 машины, но их не может быть 1,6. Таким образом, существует конечное число возможных значений, которые можно зарегистрировать в процессе наблюдений.
У дискретных переменных можно подсчитать и оценить интенсивность потока событий или сводное количество (медиана, мода, среднеквадратичное отклонение). К примеру, в 2014 году у каждой американской семьи было, в среднем, по 2,11 транспортных средства.
Обычный способ графического представления дискретных переменных — столбчатые диаграммы, где каждый отдельный столбик представляет отдельное значение, а высота столбика означает его пропорцию к целому.
2.2) Непрерывные данные
Непрерывные данные могут принимать практически любое числовое значение и могут быть разделены на меньшие части, включая дробные и десятичные значения. Непрерывные переменные часто измеряют по шкале. Когда вы измеряете высоту, вес, температуру, вы имеете дело с непрерывными данными.
Например, средний рост в Индии составляет 5 футов 9 дюймов (
175 см.) для мужчин и 5 футов 4 дюйма (
Непрерывные данные подразделяются на 2 типа:
а) Интервальные данные
Интервальные значения представлены упорядоченными единицами, которые имеют одинаковое отличие друг от друга. Таким образом, мы говорим об интервальных данных, когда есть переменная, которая содержит упорядоченные числовые значения, и нам известны точные отличия этих значений. Примером может служить температура в заданном месте:
Проблема со значениями интервальных данных в том, что у них нет “ абсолютного нуля”.
б) Данные соотношения
Данные соотношения также представляют собой упорядоченные единицы с одинаковыми отличиями друг от друга. Это практически то же самое, что и интервальные данные, однако данные соотношения имеют “ абсолютный ноль”. Подходящие примеры — высота, вес, длина и т. д.
При работе с непрерывными данными можно использовать практически все методы: процентиль, медиану, межквартильный размах, среднее арифметическое, моду, среднеквадратичное отклонение, амплитуду.
Для визуализации непрерывных данных можно воспользоваться гистограммой или диаграммой размаха. С помощью гистограммы можно определить среднее значение и крутость распределения, изменчивость и модальность. Имейте в виду, что гистограмма не показывает выбросы — для этого нужно использовать диаграмму размаха.
Заключение
Из этой статьи вы узнали о различных типах данных, используемых в статистике, о разнице между дискретными и непрерывными данными, а также о том, что собой представляют номинальные, порядковые, бинарные, интервальные данные и данные соотношения. Кроме того, теперь вы знаете, какие статистические измерения и методы визуализации можно применять для разных типов данных и как преобразовать категориальные переменные в числовые. Это позволит вам провести большую часть разведочного анализа на представленном наборе данных.
Дискретные случайные величины
Дискретная случайная величина — это такая случайная величина, значения которой могут быть не более чем счетными, то есть либо конечными, либо счетными. Под счетностью имеется ввиду, что значения случайной величины можно занумеровать.
Пример 1. Приведем примеры дискретных случайных величин:
в) число прибывших кораблей на борт (счетное множество значений).
г) число вызовов, поступающих на АТС (счетное множество значений).
1. Закон распределения вероятностей дискретной случайной величины.
$\begin
\hline
X_i & x_1 & x_2 & \dots & x_n \\
\hline
p_i & p_1 & p_2 & \dots & p_n \\
\hline
\end
$\begin
\hline
1 & 2 & 3 & 4 & 5 & 6 \\
\hline
1/6 & 1/6 & 1/6 & 1/6 & 1/6 & 1/6 \\
\hline
\end
2. Математическое ожидание дискретной случайной величины.
3. Дисперсия дискретной случайной величины.
Возможные значения случайных величин с равными математическими ожиданиями могут по-разному рассеиваться вокруг своих средних значений. Например, в двух студенческих группах средний балл за экзамен по теории вероятностей оказался равным 4, но в одной группе все оказались хорошистами, а в другой группе — только троечники и отличники. Поэтому возникает необходимость в такой числовой характеристике случайной величины, которая бы показывала разброс значений случайной величины вокруг своего математического ожидания. Такой характеристикой является дисперсия.
4. Функция распределения дискретной случайной величины.
Способ представления дискретной случайной величины в виде ряда распределения не является единственным, а главное он не является универсальным, поскольку непрерывную случайную величину нельзя задать с помощью ряда распределения. Существует еще один способ представления случайной величины — функция распределения.