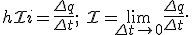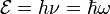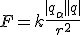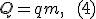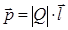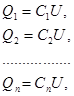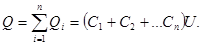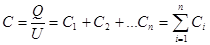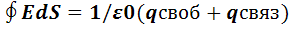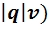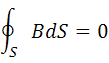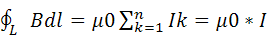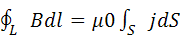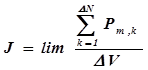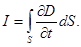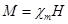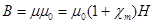Что такое дискретность электрического заряда определение

Учебники

Журнал «Квант»

Общие

§8. Электростатические взаимодействия. Электрический заряд. Закон Кулона

8.5. Дискретность электрического заряда. Объемная плотность заряда

Чрезвычайно точные измерения показали, что заряд протона по модулю в точности равен заряду электрона. Более того, другие заряженные элементарные частицы также имеют электрические заряд в точности равный заряду электрона. Таким образом, заряд электрона является минимально возможным электрическим зарядом, минимальной «порцией» электрического заряда, поэтому его называют элементарным зарядом. Многочисленные попытки, продолжающиеся и в настоящее время, обнаружить частицы, имеющие заряд, меньший элементарного, закончились неудачей. Так как заряды тел обусловлены избытком или недостатком электронов, то их заряд оказывается кратным элементарному заряду.

Первые теории электричества строились на представлении о заряде, как некоторой особой электрической жидкости (о молекулярной структуре настоящих жидкостей тогда тоже не было известно). Долгие споры велись о том, сколько электрических жидкостей существует, одна или две. Отголоски этих жидкостных представлений дошли до нас в многочисленных терминах – заряд перетекает (отсюда электрический ток), конденсатор обладает электрической емкостью (показывающий сколько электрической жидкости он может вместить), и др. Электрон, а следовательно и элементарный заряд, был открыт только в 1897 году английским физиком Дж. Дж. Томсоном.

Дискретность электрического заряда проявляется только в том случае, когда заряды тел малы, сравнимы с элементарным зарядом. Не случайно Р. Милликен в своих экспериментах использовал микроскопические капельки, заряды которых составляли несколько элементарных зарядов. Во многих случаях нет необходимости учитывать дискретность электрического заряда. То есть в математическом описании перейти к непрерывному описанию распределения зарядов. В этом случае можно ввести понятие объемной плотности заряда как функции координат ρ(x, y, z), как отношение величины заряда Δq, содержащегося в малом объеме ΔV вокруг точки с координатами (x, y, z), к величине этого объема

\(\rho \left(x,y,z \right) = \frac< \Delta q>< \Delta V>\) при \(\Delta V \rightarrow 0\)

Это определение полностью совпадает с обсуждавшимся ранее понятием плотности «в точке».

Источник

Электрический заряд. Дискретность заряда. Закон сохранения электрического заряда Закон Кулона

ЭЛЕКТРОСТАТИКА

Электрический заряд. Дискретность заряда. Закон сохранения электрического заряда Закон Кулона.

По современным представлениям, электрический заряд является скалярной физической величиной, которая характеризует способность тел вступать в электромагнитные взаимодействия и его величина определяет интенсивность этих взаимодействий.

Что же представляет собой электрический заряд? Для того, чтобы составить себе представление об этом понятии, можно перечислить свойства, которыми обладают электрические заряды.

2) Электрический заряд величина релятивистски инвариантная, т.е. он не изменяется при движении с любыми скоростями и не зависит от выбора системы отсчета.

3) Заряд обладает свойством аддитивности, т.е. заряд любой системы равняется алгебраической сумме зарядов частиц, составляющих эту систему.

4) Электрический заряд – дискретен, т.е. заряды всех тел и частиц, вступающих в электрические взаимодействия, состоят из целого числа элементарных зарядов. В природе в свободном состоянии существуют частицы, имеющие минимальный по модулю заряд, равный . Поэтому

, (1.1)

5) М. Фарадеем был сформулирован закон сохранения заряда: в любой электроизолированной системе алгебраическая сумма электрических зарядов остается величиной постоянной

Замкнутая система: const. (1.2)

В 1785 году Ш Кулоном с помощью изобретенных им крутильных весов экспериментально был установлен закон взаимодействия неподвижных точечных зарядов. «Точечным» называется заряд, сосредоточенный на теле, линейные размеры которого пренебрежимо малы по сравнению с расстояниями до других заряженных тел, с которыми он взаимодействует. Закон Кулона:силы, с которыми взаимодействуют два неподвижных точечных заряда в вакууме, прямо пропорциональны произведению этих зарядов и обратно пропорциональны квадрату расстояния между ними; силы направлены вдоль прямой, соединяющей эти заряды:

, (1.3)

где — сила, с которой первый заряд действует на второй заряд, а — радиус – вектор, проведенный от первого заряда ко второму заряду.

Входящая в формулу (1.3) величина Ф/м называется электрической постоянной, она возникает при записи формулы закона в международной системе единиц СИ, а коэффициент k пропорциональности, зависящий от выбора системы единиц в системе СИ равен

.

Если взаимодействующие заряды находятся в однородной и изотропной диэлектрической среде, то в знаменателе формулы (1.3) появляется безразмерная величина — диэлектрическая проницаемость среды, которая показывает во сколько раз сила взаимодействия зарядов в данной среде меньше, чем их сила взаимодействия в вакууме.

Для вакуума ε = 1, для всех сред ε>1, но с достаточной степенью точности при проведении многих расчетов можно принять для газов ( и для воздуха).

Источник

Электрический заряд и его свойства. Дискретность. Элементарный электрический заряд. Закон сохранения электрического заряда.

Электрический заряд и его свойства. Дискретность. Элементарный электрический заряд. Закон сохранения электрического заряда.

Электрический заряд – это физическая величина, характеризующая электромагнитное взаимодействие. Тело заряжено отрицательно, если на нем избыток электронов, положительно – дефицит.

Перечислим свойства зарядов

2. Электрический заряд имеет дискретную природу. Это означает, что заряд любого тела кратен заряду электрона q=Nqe, где N – целое число. Однако мы, как правило, не замечаем дискретности заряда, так как элементарный заряд очень мал.

3. В изолированной системе, т.е. в системе, тела которой не обмениваются зарядами с внешними по отношению к ней телами, алгебраическая сумма зарядов сохраняется (закон сохранения заряда).

4. Эл. заряд всегда можно передать от одного тела к другому.

5. Единица заряда в СИ – кулон (Кл). По определению, 1 кулон равен заряду, протекающему через поперечное сечение проводника за 1 с при силе тока 1 А.

6. Закон сохранения электрического заряда.

Внутри замкнутой системы при любых взаимодействиях алгебраическая сумма электрических зарядов остается постоянной:

Изолированной (или замкнутой) системой мы будем называть систему тел, в которую не вводятся извне и не выводятся из нее электрические заряды.

Нигде и никогда в природе не возникает и не исчезает электрический заряд одного знака. Появление положительного электрического заряда всегда сопровождается появлением равного по модулю отрицательного заряда. Ни положительный, ни отрицательный заряд не могут исчезнуть в отдельности, они могут лишь взаимно нейтрализовать друг друга, если равны по модулю.

Так элементарные частицы способны превращаться друг в друга. Но всегда при рождении заряженных частиц наблюдается появление пары частиц с зарядами противоположного знака. Может наблюдаться и одновременное рождение нескольких таких пар. Исчезают заряженные частицы, превращаясь в нейтральные, тоже только парами. Все эти факты не оставляют сомнений в строгом выполнении закона сохранения электрического заряда.

Электрический ток. Условия существования эл.тока. Сила тока и плотность тока

Электрическим током называется направленное движение заряженных частиц. За направление электрического тока условились считать направление движения положительно заряженных частиц. Для продолжительного существования электрического тока в замкнутой цепи необходимо выполнение следующих условий:

-наличие свободных заряженных частиц (носителей тока);

-наличие электрического поля, силы которого, действуя на заряженные частицы, заставляют их двигаться упорядоченно;

— наличие источника тока, внутри которого сторонние силы перемещают свободные заряды против электростатических (кулоновских) сил.

Количественными характеристиками электрического тока являются сила тока I и плотность тока j.

Сила тока — скалярная физическая величина, равная отношением заряда Δq, проходящего через поперечное сечение проводника за некоторый промежуток времени Δt, к этому промежутку:

Единицей силы тока в СИ является ампер (А).

Если сила тока и его направление со временем не изменяются, то ток называется постоянным.

Плотность тока j — это векторная физическая величина, модуль которой равен отношению силы тока I в проводнике к площади S поперечного сечения проводника:

В СИ единицей плотности тока является ампер на квадратный метр (А/м2).

Преломление света в линзах

Линзой называется прозрачное тело, ограниченное двумя криволинейными или криволинейной и плоской поверхностями.

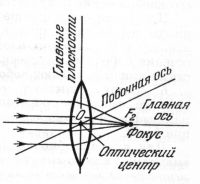
В большинстве случаев применяются линзы, поверхности которых имеют сферическую форму. Линза называется тонкой, если ее толщина d мала по сравнению с радиусами кривизны ее поверхностей R1 и R2. В противном случае линза называется толстой. Главной оптической осью линзы называют прямую, проходящую через центры кривизны ее поверхностей. Можно считать, что в тонкой линзе точки пересечения главной оптической оси с обеими поверхностями линзы сливаются в одну точку О, называемую оптическим центром линзы. Тонкая линза имеет одну главную плоскость, общую для обеих поверхностей линзы и проходящую через оптический центр линзы перпендикулярно к ее главной оптической оси. Все прямые, проходящие через оптический центр линзы и не совпадающие с ее главной оптической осью, называют побочными оптическими осями линзы. Лучи, идущие вдоль оптических осей линзы (главной и побочных), не испытывают преломления.

Формула тонкой линзы:

где п21 = п2/п1, п2 и n1 — абсолютные показатели преломлениядля материала линзы и окружающей среды, R1 и R2 — радиусы кривизны передней и задней (относительно предмета) поверхностей линзы, а1 и а2 — расстояния до предмета и его изображения, отсчитываемые от оптического центра линзы вдоль ее главной оптической оси.

Величину называют фокусным расстоянием линзы. Точки, лежащие на главной оптической оси линзы по обе стороны от оптического центра па одинаковых расстояниях, равных f, называют главными фокусами линии. Плоскости, проходящие через главные фокусы F1 и F2 линзы перпендикулярно к ее главной оптической оси, называют фокальными плоскостями линзы. Точки пересечения побочных оптических осей с фокальными плоскостями линзы называют побочными фокусами линзы.

Линзу называют собирающей (положительной), если ее фокусное расстояние f >0. Линзу называют рассеивающей (отрицательной), если ее фокусное расстояние f n1 собирающими линзами являются двояковыпуклые, плоско-выпуклые и вогнуто-выпуклые (положительные менисковые линзы), утоньшающиеся от центра к краям; рассеивающими являются двояковогнутые, плоско-вогнутые и выпукло-вогнутые линзы (отрицательные мениски), утолщающиеся от центра к краям. Для п2 n1.

Гипотеза Планка. Фотон и его свойства. Корпускулярно-волновой дуализм

Гипо́теза Пла́нка — гипотеза, выдвинутая 14 декабря 1900 года Максом Планком и заключающаяся в том, что при тепловом излучении энергия испускается и поглощается не непрерывно, а отдельными квантами (порциями). Каждая такая порция-квант имеет энергию 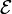, пропорциональной частоте ν излучения:

где h или 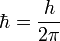— коэффициент пропорциональности, названный впоследствии постоянной Планка. На основе этой гипотезы он предложил теоретический вывод соотношения между температурой тела и испускаемым этим телом излучением — формулу Планка.

Позднее гипотеза Планка была подтверждена экспериментально.

Выдвижение этой гипотезы считается моментом рождения квантовой механики.

Основные свойства фотона

1. Является частицей электромагнитного поля.

2. Движется со скоростью света.

3. Существует только в движении.

4. Остановить фотон нельзя: он либо движется со скоростью, равной скорости света, либо не существует; следовательно, масса покоя фотона равна нулю.

Энергия фотона:

Согласно теории относительности энергия всегда может быть вычислена как ,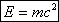

Импульс фотона 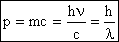. Импульс фотона направлен по световому пучку.

Конец XIX в.: фотоэффект и эффект Комптона подтвердили теорию Ньютона, а явления дифракции, интерференции света подтвердили теорию Гюйгенса.

Таким образом, многие физики в начале XX в. пришли к выводу, что свет обладает двумя свойствами:

1. При распространении он проявляет волновые свойства.

2. При взаимодействии с веществом проявляет корпускулярные свойства. Его свойства не сводятся ни к волнам, ни к частицам.

Опыты Резерфорда. Планетарная модель атома

Для экспериментального исследования распределения положительного заряда, а значит, и массы внутри атома Резерфорд предложил в 1906 г. применить зондирование атома с помощью α-частиц. Их масса примерно в 8000 раз больше массы электрона, а положительный заряд равен по модулю удвоенному заряду электрона. Скорость α-частиц очень велика: она составляет 1/15 скорости света. Этими частицами Резерфорд бомбардировал атомы тяжелых элементов. Электроны вследствие своей малой массы не могут заметно изменить траекторию α-частицы и не в состоянии заметно изменить его скорость. Рассеяние (изменение направления движения) α-частиц может вызвать только положительно заряженная часть атома. Таким образом, по рассеянию α-частиц можно определить характер распределения положительного заряда и массы внутри атома. Радиоактивный препарат, например радий, помещался внутри свинцового цилиндра 1, вдоль которого был высверлен узкий канал. Пучок α-частиц из канала падал на тонкую фольгу 2 из исследуемого материала (золото, медь и пр.). После рассеяния α-частицы попадали на полупрозрачный экран 3, покрытый сульфидом цинка. Столкновение каждой частицы с экраном сопровождалось вспышкой света (сцинтилляцией), которую можно было наблюдать в микроскоп 4. Весь прибор размещался в сосуде, из которого был откачан воздух.

При распределении по всему атому положительный заряд не может создать достаточно интенсивное электрическое поле, способное отбросить а-частицу назад. Максимальная сила отталкивания определяется по закону Кулона:

где qα — заряд α-частицы; q — положительный заряд атома; r — его радиус; k — коэффициент пропорциональности. Напряженность электрического поля равномерно заряженного шара максимальна на поверхности шара и убывает до нуля по мере приближения к центру. Поэтому, чем меньше радиус r, тем больше сила, отталкивающая α-частицы. Эта теория кажется совершенно необходимой для объяснения опытов по рассеиванию а-частиц. Но на основе этой модели нельзя объяснить факт существования атома, его устойчивость. Ведь движение электронов по орбитам происходит с ускорением, причем весьма немалым. Ускоренно движущийся заряд по законам электродинамики Максвелла должен излучать электромагнитные волны с частотой, равной частоте его обращения вокруг ядра. Излучение сопровождается потерей энергии. Теряя энергию, электроны должны приближаться к ядру, подобно тому как спутник приближается к Земле при торможении в верхних слоях атмосферы. Как показывают строгие расчеты, основанные на механике Ньютона и электродинамике Максвелла, электрон за ничтожно малое время должен упасть на ядро. Атом должен прекратить свое существование.

В действительности ничего подобного не происходит. Отсюда следует, что к явлениям атомных масштабов законы классической физики неприменимы. Резерфорд создал планетарную модель атома: электроны обращаются вокруг ядра, подобно тому как планеты обращаются вокруг Солнца. Эта модель проста, обоснована экспериментально, но не позволяет объяснить устойчивость атома.

Количество теплоты

Количество теплоты — это мера изменения внутренней энергии, которую тело получает (или отдает) в процессе теплообмена.

Таким образом, и работа, и количество теплоты характеризуют изменение энергии, но не тождественны энергии. Они не характеризуют само состояние системы, а определяют процесс перехода энергии из одного вида в другой (от одного тела к другому) при изменении состояния и существенно зависят от характера процесса.

Основное различие между работой и количеством теплоты состоит в том, что работа характеризует процесс изменения внутренней энергии системы, сопровождающийся превращением энергии из одного вида в другой (из механической во внутреннюю). Количество теплоты характеризует процесс передачи внутренней энергии от одних тел к другим (от более нагретых к менее нагретым), не сопровождающийся превращениями энергии.

Опыт показывает, что количество теплоты, необходимое для нагревания тела массой m от температуры T1 до температуры T2, рассчитывается по формуле где c — удельная теплоемкость вещества;

Единицей удельной теплоемкости в СИ является джоуль на килограмм-Кельвин (Дж/(кг·К)).

Удельная теплоемкость c численно равна количеству теплоты, которое необходимо сообщить телу массой 1 кг, чтобы нагреть его на 1 К.

Теплоемкость тела CT численно равна количеству теплоты, необходимому для изменения температуры тела на 1 К:

Единицей теплоемкости тела в СИ является джоуль на Кельвин (Дж/К).

Для превращения жидкости в пар при неизменной температуре необходимо затратить количество теплоты

где L — удельная теплота парообразования. При конденсации пара выделяется такое же количество теплоты.

Для того чтобы расплавить кристаллическое тело массой m при температуре плавления, необходимо телу сообщить количество теплоты

где λ — удельная теплота плавления. При кристаллизации тела такое же количество теплоты выделяется.

Количество теплоты, которое выделяется при полном сгорании топлива массой m,

где q — удельная теплота сгорания.

Единица удельных теплот парообразования, плавления и сгорания в СИ — джоуль на килограмм (Дж/кг).

Электрический заряд и его свойства. Дискретность. Элементарный электрический заряд. Закон сохранения электрического заряда.

Электрический заряд – это физическая величина, характеризующая электромагнитное взаимодействие. Тело заряжено отрицательно, если на нем избыток электронов, положительно – дефицит.

Перечислим свойства зарядов

2. Электрический заряд имеет дискретную природу. Это означает, что заряд любого тела кратен заряду электрона q=Nqe, где N – целое число. Однако мы, как правило, не замечаем дискретности заряда, так как элементарный заряд очень мал.

3. В изолированной системе, т.е. в системе, тела которой не обмениваются зарядами с внешними по отношению к ней телами, алгебраическая сумма зарядов сохраняется (закон сохранения заряда).

4. Эл. заряд всегда можно передать от одного тела к другому.

5. Единица заряда в СИ – кулон (Кл). По определению, 1 кулон равен заряду, протекающему через поперечное сечение проводника за 1 с при силе тока 1 А.

6. Закон сохранения электрического заряда.

Внутри замкнутой системы при любых взаимодействиях алгебраическая сумма электрических зарядов остается постоянной:

Изолированной (или замкнутой) системой мы будем называть систему тел, в которую не вводятся извне и не выводятся из нее электрические заряды.

Нигде и никогда в природе не возникает и не исчезает электрический заряд одного знака. Появление положительного электрического заряда всегда сопровождается появлением равного по модулю отрицательного заряда. Ни положительный, ни отрицательный заряд не могут исчезнуть в отдельности, они могут лишь взаимно нейтрализовать друг друга, если равны по модулю.

Так элементарные частицы способны превращаться друг в друга. Но всегда при рождении заряженных частиц наблюдается появление пары частиц с зарядами противоположного знака. Может наблюдаться и одновременное рождение нескольких таких пар. Исчезают заряженные частицы, превращаясь в нейтральные, тоже только парами. Все эти факты не оставляют сомнений в строгом выполнении закона сохранения электрического заряда.

Источник

Вопрос№1. Электрический заряд. Дискретность заряда. Закон сохранения электрического заряда. Взаимодействие зарядов. Закон Кулона.

Вопрос№1. Электрический заряд. Дискретность заряда. Закон сохранения электрического заряда. Взаимодействие зарядов. Закон Кулона.

Вопрос№3.Электрический диполь и его поле.

Вектор 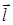, направленный по оси диполя (прямой, проходящей через оба заряда) от отрицательного заряда к положительному и равный расстоянию между ними, называется плечом диполя.

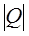
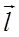
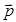
Вектор, совпадающий по направлению с плечом диполя и равный произведению заряда на плечо , называется электрическим моментом диполя или дипольным моментом.

Согласно принципу суперпозиции, напряженность поля диполя в произвольной точке

где и — напряженности полей, создаваемых соответственно положительным и отрицательным зарядами.

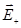
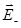
Поле равномерно заряженной бесконечной плоскости.

Поле объемно заряженного шара.

Напряженность поля вне равномерно заряженного шара описывается формулой : ( ),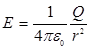

а внутри его изменяется линейно с расстоянием согласно выражению ( ).

Соединение конденсаторов.

У параллельно соединен­ных конденсаторов разность потенциалов на обкладках конденсаторов одинакова и равна .

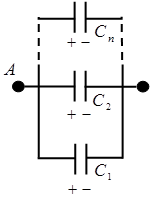
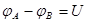
если емкости отдельных конденсаторов 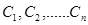, то их заряды равны

а заряд батареи конденсаторов

Полная емкость батареи:

т. е. при параллельном соединении кон­денсаторов она равна сумме емкостей от­дельных конденсаторов.

У последовательно соединенных конденсаторов заряды всех обкладок равны по модулю, а разность потенциалов на зажимах батареи:

,

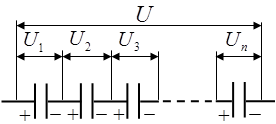
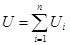
где для любого из рассматриваемых кон­денсаторов:

,

, откуда ,

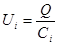
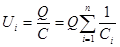
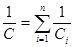
т. е. при последовательном соединении конденсаторов суммируются величины, об­ратные емкостям.

Теорема.

Теорема гаусса для электростатического поля в вакууме может быть распространена на электростатическое поле в среде, если под q понимать сумму всех свободных и связанных зарядов, охватываемых замкнутой гауссовой поверхностью S:

Напряженность электростатического поля, согласно Е=Е₀/(1+ 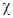)=Е₀/e, зависит от свойств среды: в однородной изотропной среде напряженность поля Е обратно пропорциональна e. Вектор напряженности Е, переходя через границу диэлектриков, претерпевает скачко­образное изменение. Поле характеризуется еще вектором электрического смещения, который для электрически изотроп­ной среды, по определению, равен

D=e₀eE.

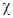
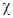
Используя формулы e =1+ и Р= e₀Е, вектор электрического смещения можно выразить как

D=e₀E+P.

— диэлектрическая восприимчивость вещества,

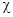
Сторонние силы. Э.Д.С.,

Против сил электрического поля могут действовать только силы неэлектрического происхождения, поэтому такие силы называются сторонними.

Сторонние силы — это силы неэлектрического происхождения, которые в отличие от кулоновских сил вызывают не соединение, а разделение разноименных электрических зарядов и поддерживают разность потенциалов проводников.

Электродвижущая сила – численно равна работе, совершаемой сторонними силами при перемещении по участку цепи единичного положительного заряда. –электродвижущая сила, действующая на участок цепи.

а) цепь замкнута:

б) Э.Д.С. на участке отсутствует:

Участок на котором отсутствует Э.Д.С. называется однородным, а участок содержащий Э.Д.С. называется неоднородным.

Закон Ома для участка цепи

Для участка цепи содержащей ЭДС будет иметь вид

Вопрос№15. Правила Киргофа и расчет электрических цепей.

Электрическая цепь- это система соединенных между собой токопроводящих элементов цепи. Если цепь состоит только из линейных эле­ментов, то она линейна, если же цепь содержит хотя бы один нелиней­ный элемент, то она становится нелинейной. Электрическая цепь изображается графически в виде своей эквива­лентной электрической схемы, на которой показано условное изобра­жение её элементов и соединение их друг с другом.

Физической основой расчёта электрической цепи, как линейной так и нелинейной являются законы Кирхгофа, первый из которых относит­ся к узлам цепи, а второй — к простым контурам.

Первый закон Кирхгофа (для узлов): алгебраическая сумма притека­ющих и вытекающих токов для любого узла цепи равна нулю:

(1)

В уравнении (1) притекающие и вытекающие токи берутся с противо­положными знаками.

Второй закон Кирхгофа (для контуров): алгебраическая сумма паде­ний напряжений на элементах цепи вдоль любого замкнутого конту­ра равна алгебраической сумме ЭДС, действующих в данном контуре

(2)

В уравнении (2) знаки величин U_k и E_k определяются по отношению к выбранному направлению обхода контура. Если ток I_k совпадает с на­правлением обхода, то падение напряжения на данном элементе U_k считается положительным, в противном случае оно отрицательно. Элек­тродвижущая сила E_k считается положительной, если её поле сторон­них сил совпадает с направлением обхода контура, в противном слу­чае она отрицательна. (Поле сторонних сил всегда направлено внутри источника от отрицательного к положительному полюсу).

Если элемент цепи не генерирует ЭДС, то падение напряжения на нём совпадает с разностью потенциалов на элементе. Для линейного эле­мента оно определяется 1 из закона Ома по заданному току и сопротив­лению . Для нелинейного элемента, не подчиняющегося зако­ну Ома, такое определение падения напряжения невозможно, в дан­ном случае оно определяется только из ВАХ нелинейного элемента по заданному току.

Источники магнитного поля

Магнитное поле создается (порождается) током заряженных частиц, или изменяющимся во времени электрическим полем, или собственными магнитными моментами частиц (последние для единообразия картины могут быть формальным образом сведены к электрическим токам).

Основной силовой характеристикой магнитного поля является вектор магнитной индукции 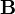(вектор индукции магнитного поля).

Вектор магнитной индукции В численно равен отношению силы, действующей на заряж. частицу со стороны магнитного поля, к произведению абсолютного значения заряда и скорости частицы, если направление скорости частицы таково, что эта сила максимальна. В=(F)max/(

Сила Лоренса.

На частицу движущуюся в магнитном поле, действует Сила Лоренса определяющаяся выражением:F=q[vхB]. Модуль магнитной силы равен: F=qvB sin a

Направление силы Лоренса «правило левой руки»:если ладонь левой руки расположить так, чтобы вектор магнитной индукции В входил в ладонь, а 4 пальца направить вдоль скорости + частицы, то отставленный на 90 градусов большой палец укажет направление силы Лоренса.Если имеются одновременно электрическое и магнитное поля, сила, действующая на заряженную частицу, равна F=qE+q[vхB]

Теорема Гаусса

Магнитный поток сквозь произвольную замкнутую поверхность равен нулю:

Пусть ток I течет по проводнику, намотанному по винтовой линии на поверхность цилиндра. Такой обтекаемый током цилиндр называют соленоидом. Пусть на единицу длины соленоида приходится n витков проводника. Если шаг винтовой линии достаточно мал, то каждый виток соленоида можно приближенно заменить замкнутым витком. Будем также предполагать, что сечение проводника настолько мало, что ток в соленоиде можно считать текущим по его поверхности.

Опыт и расчет показывают, что чем длиннее соленоид, тем меньше индукция магнитного поля снаружи его. Для бесконечно длинного соленоида магнитное поле снаружи отсутствует вообще. Из изображения симметрии ясно, что линии вектора В внутри соленоида направлены вдоль его оси, причем вектор В составляет с направлением тока в соленоиде правовинтную систему.

Уже то, что мы выяснили относительно конфигурации магнитного поля соленоида, подсказывает выбрать прямоугольный контур так как показано на Рис. 13. Циркуляция вектора В по данному контуру равна Bl, и контур охватывает ток nlI. Согласно теореме о циркуляции, откуда следует, что внутри длинного соленоида Т.е. поле внутри длинного соленоида однородно (за исключением областей, прилегающих к торцам соленоида, но этим при расчетах зачастую пренебрегают). Произведение nI называют числом ампервитков.

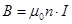
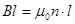
Закон полного тока для магнитного поля в веществе (теорема о циркуляции вектора B).

Циркуляция магнитной индукции поля в вакууме вдоль произвольного замкнутого контура L равна произведению магнитной постоянной на алгебраическую сумму токов, охватываемых этим контуром(т.е. на электрический ток через поверхность S, натянутую на этот контур)

Закон полного тока можно записать в виде:

j-плотность тока в пределах малого элемента dS поверхности S, натянутой на контур L.

Намагниченность

Для характеристики степени намагничивания того или иного вещества используется понятие намагниченности J, которая равна магнитному моменту единицы объема магнетика:

Другими словами, намагниченность J – это количественная мера намагничивания вещества.

Магнитная проницаемость

Магнитная проницаемость является количественной характеристикой, определяющей изменение поля в веществе. Это безразмерная величина, которая, как правило, находится экспериментально:

Она показывает, во сколько раз магнитная индукция B в вытянутом (длинном) образце, помещенном в длинный соленоид (соленоид мы приводим в качестве примера) отличается от магнитной индукции 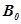в пустом соленоиде (т.е. в вакууме). Значения магнитной проницаемости сильно зависят от состава и строения вещества, т.е. от рода (типа) магнетика.

Все вещества при рассмотрении их магнитных свойств принято называть магненитками.Три основные группы магнетиков:

Диамагнетики; Парамагнетики; Ферромагнетики;

Диамагнетикаминазывают вещества, которые намагничиваются во внешнем магнитном поле в направлении, противоположном направлению вектора магнитной индукции поля. К диамагнетикам относятся вещества, магнитные моменты атомов, молекул или ионов которых в отсутствие внешнего магнитного поля равна нулю. Диамагнетиками являются инертные газы, молекулярные водород и азот, висмут, цинк, медь, нафталин и т.д.

Намагниченность диамагнетиков: J=n ,где – магнитный момент, n0-концентрация атомов.

Парамагнетикаминазываются вещества, которые намагничиваются во внешнем магнитном поле в направление вектора B. К парамагнетикам относятся многие металлы, некоторые переходные металлы, а также сплавы этих металлов., кислород, оксид азота, оксид марганца. В отсутствии внешнего магнитного поля парамагнетик не намагничен, так как из-за теплового движения собственные магнитные моменты атомов ориентированы совершенно беспорядочно(J=0).при внесении парамагнетического вещества в магнитное поле парамагнетик намагничивается «по полю», т.е. в направлении B.

Намагниченность парамагнетиков зависит от параметра a=PmB/(kT), где k-постоянная Больцмана, T-термодинамическая температура. J=n0PmL(a), где n0-концентрация атомов парамагнетика.

Ток смещения.

Для установления количественных соотношений между изменяющимся электрическим полем Максвелл вел в рассмотрение так называемый ток смещения.

Рассмотрим цепь переменного тока, содержащую конденсатор.

Между обкладками заряжающегося и разряжающего конденсатора имеется переменное электрическое поле, поэтому, согласно Максвеллу, через конденсатор “протекают” токи смещения, причем в тех участках, где отсутствуют проводники.

По Максвеллу, переменное электрическое поле в конденсаторе в каждый момент времени создает такое магнитное поле, как если бы между обкладками конденсатора существовал ток проводимости, равный току в проводящих проводах. Тогда можно утверждать, что токи проводимости ( 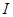) и смещения ( ) равны. Ток проводимости вблизи обкладок конденсатора для общего случая можно записать так:

Сравнивая это выражение с , имеем . (3)

Данное выражение было названо Максвеллом плотностью тока смещения. Направление вектора , а следовательно, и вектора совпадает с направлением вектора , как это следует из формулы (3).

Подчеркнем, что из всех физических свойств, присущих току проводимости, Максвелл приписал току смещения лишь одно – способность создавать в окружающем пространстве магнитное поле. Следует отметить, что ток смещения по своей сути – это изменяющееся со временем электрическое поле. Ток смещения поэтому существует не только в вакууме или в диэлектриках, но и внутри проводников по которым течет переменный ток. Однако в данном случае он пренебрежительно мал по сравнению с током проводимости.

Максвелл обобщил закон полного тока, добавив в правую часть уравнения ток смещения сквозь поверхность, натянутую на замкнутый контур L:

Второе уравнения Максвелла: циркуляция вектора Н напряженности магнитного поля по произвольному неподвижному замкнутому контуру L, мысленно проведенному в электромагнитном поле, равна алгебраической сумме макротоков и тока смещения сквозь поверхность, натянутую на этот контур.

Материальные уравнения

В слабых электромагнитных полях, сравнительно медленно меняющихся в пространстве и во времени, в случае изотропных, неферромагнитных и несегнетоэлектрических сред справедливо приближение, в котором поляризуемость и намагниченность линейно зависят от приложенных полей.

СИ: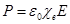

СИ: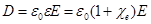

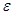
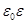
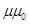
где — относительная диэлектрическая проницаемость, — относительная магнитная проницаемость. Размерные величины (в единицах СИ — Ф/м) и (в единицах СИ — Гн/м), возникающие в системе СИ, называются абсолютная диэлектрическая проницаемость и абсолютная магнитная проницаемость соответственно.

Вопрос№1. Электрический заряд. Дискретность заряда. Закон сохранения электрического заряда. Взаимодействие зарядов. Закон Кулона.

Источник