Что такое динамическое программирование

Динамическое программирование для начинающих

Динамическое программирование — тема, которой в рунете посвящено довольно мало статей, поэтому мы решили ею заняться. В этой статье будут разобраны классические задачи на последовательности, одномерную и двумерную динамику, будет дано обоснование решениям и описаны разные подходы к их реализации. Весь приведённый в статье код написан на Java.

О чём вообще речь? Что такое динамическое программирование?

Хорошо, как это использовать?

Решение задачи динамическим программированием должно содержать следующее:

И что, мне для решения рекурсивный метод писать надо? Я слышал, они медленные.

Конечно, не надо, есть и другие подходы к реализации динамики. Разберём их на примере следующей задачи:

Идея решения

Здесь нам даны и начальные состояния (a₀ = a₁ = 1), и зависимости. Единственная сложность, которая может возникнуть — понимание того, что 2n — условие чётности числа, а 2n+1 — нечётности. Иными словами, нам нужно проверять, чётно ли число, и считать его в зависимости от этого по разным формулам.

Рекурсивное решение

Очевидная реализация состоит в написании следующего метода:

Рекурсивное решение с кэшированием значений

Идея мемоизации очень проста — единожды вычисляя значение, мы заносим его в какую-то структуру данных. Перед каждым вычислением мы проверяем, есть ли вычисляемое значение в этой структуре, и если есть, используем его. В качестве структуры данных можно использовать массив, заполненный флаговыми значениями. Если значение элемента по индексу N равно значению флага, значит, мы его ещё не вычисляли. Это создаёт определённые трудности, т.к. значение флага не должно принадлежать множеству значений функции, которое не всегда очевидно. Лично я предпочитаю использовать хэш-таблицу — все действия в ней выполняются за O(1), что очень удобно. Однако, при большом количестве значений два числа могут иметь одинаковый хэш, что, естественно, порождает проблемы. В таком случае стоит использовать, например, красно-чёрное дерево.

Для уже написанной функции f(int) кэширование значений будет выглядеть следующим образом:

Не слишком сложно, согласитесь? Зато это избавляет от огромного числа операций. Платите вы за это лишним расходом памяти.

Последовательное вычисление

Теперь вернёмся к тому, с чего начали — рекурсия работает медленно. Не слишком медленно, чтобы это приносило действительные неприятности в настоящей жизни, но на соревнованиях по спортивному программированию каждая миллисекунда на счету.

Метод последовательного вычисления подходит, только если функция ссылается исключительно на элементы перед ней — это его основной, но не единственный минус. Наша задача этому условию удовлетворяет.

Суть метода в следующем: мы создаём массив на N элементов и последовательно заполняем его значениями. Вы, наверное, уже догадались, что таким образом мы можем вычислять в том числе те значения, которые для ответа не нужны. В значительной части задач на динамику этот факт можно опустить, так как для ответа часто бывают нужны как раз все значения. Например, при поиске наименьшего пути мы не можем не вычислять путь до какой-то точки, нам нужно пересмотреть все варианты. Но в нашей задаче нам нужно вычислять приблизительно log₂(N) значений (на практике больше), для 922337203685477580-го элемента (MaxLong/10) нам потребуется 172 вычисления.

Ещё одним минусом такого подхода является сравнительно большой расход памяти.

Создание стека индексов

Сейчас нам предстоит, по сути, написать свою собственную рекурсию. Идея состоит в следующем — сначала мы проходим «вниз» от N до начальных состояний, запоминая аргументы, функцию от которых нам нужно будет вычислять. Затем возвращаемся «вверх», последовательно вычисляя значения от этих аргументов, в том порядке, который мы записали.

Зависимости вычисляются следующим образом:

Полученный размер стека — то, сколько вычислений нам потребуется сделать. Именно так я получил упомянутое выше число 172.

Теперь мы поочередно извлекаем индексы и вычисляем для них значения по формулам — гарантируется, что все необходимые значения уже будут вычислены. Хранить будем как раньше — в хэш-таблице.

Все необходимые значения вычислены, осталось только написать

Конечно, такое решение гораздо более трудоёмкое, однако это того стоит.

Хорошо, математика — это красиво. А что с задачами, в которых не всё дано?

Для большей ясности разберём следующую задачу на одномерную динамику:

На вершине лесенки, содержащей N ступенек, находится мячик, который начинает прыгать по ним вниз, к основанию. Мячик может прыгнуть на следующую ступеньку, на ступеньку через одну или через 2. (То есть, если мячик лежит на 8-ой ступеньке, то он может переместиться на 5-ую, 6-ую или 7-ую.) Определить число всевозможных «маршрутов» мячика с вершины на землю.

Идея решения

На первую ступеньку можно попасть только одним образом — сделав прыжок с длиной равной единице. На вторую ступеньку можно попасть сделав прыжок длиной 2, или с первой ступеньки — всего 2 варианта. На третью ступеньку можно попасть сделав прыжок длиной три, с первой или со втрой ступенек. Т.е. всего 4 варианта (0->3; 0->1->3; 0->2->3; 0->1->2->3). Теперь рассмотрим четвёртую ступеньку. На неё можно попасть с первой ступеньки — по одному маршруту на каждый маршрут до неё, со второй или с третьей — аналогично. Иными словами, количество путей до 4-й ступеньки есть сумма маршрутов до 1-й, 2-й и 3-й ступенек. Математически выражаясь, F(N) = F(N-1)+F(N-2)+F(N-3). Первые три ступеньки будем считать начальными состояниями.

Реализация через рекурсию

Здесь ничего хитрого нет.

Реализация через массив значений

Исходя из того, что, по большому счёту, простое решение на массиве из N элементов очевидно, я продемонстрирую тут решение на массиве всего из трёх.

Так как каждое следующее значение зависит только от трёх предыдущих, ни одно значение под индексом меньше i-3 нам бы не пригодилось. В приведённом выше коде мы записываем новое значение на место самого старого, не нужного больше. Цикличность остатка от деления на 3 помогает нам избежать кучи условных операторов. Просто, компактно, элегантно.

Там вверху ещё было написано про какую-то двумерную динамику.

С двумерной динамикой не связано никаких особенностей, однако я, на всякий случай, рассмотрю здесь одну задачу и на неё.

В прямоугольной таблице NxM в начале игрок находится в левой верхней клетке. За один ход ему разрешается перемещаться в соседнюю клетку либо вправо, либо вниз (влево и вверх перемещаться запрещено). Посчитайте, сколько есть способов у игрока попасть в правую нижнюю клетку.

Идея решения

Логика решения полностью идентична таковой в задаче про мячик и лестницу — только теперь в клетку (x,y) можно попасть из клеток (x-1,y) или (x, y-1). Итого F(x,y) = F(x-1, y)+F(x,y-1). Дополнительно можно понять, что все клетки вида (1,y) и (x,1) имеют только один маршрут — по прямой вниз или по прямой вправо.

Реализация через рекурсию

Ради всего святого, не нужно делать двумерную динамику через рекурсию. Уже было упомянуто, что рекурсия менее выгодна, чем цикл по быстродействию, так двумерная рекурсия ещё и читается ужасно. Это только на таком простом примере она смотрится легко и безобидно.

Реализация через массив значений

Классическое решение динамикой, ничего необычного — проверяем, является ли клетка краем, и задаём её значение на основе соседних клеток.

Отлично, я всё понял. На чём мне проверить свои навыки?

В заключение приведу ряд типичных задач на одномерную и двумерную динамику, разборы прилагаются.

Взрывоопасность

При переработке радиоактивных материалов образуются отходы двух видов — особо опасные (тип A) и неопасные (тип B). Для их хранения используются одинаковые контейнеры. После помещения отходов в контейнеры последние укладываются вертикальной стопкой. Стопка считается взрывоопасной, если в ней подряд идет более одного контейнера типа A. Стопка считается безопасной, если она не является взрывоопасной. Для заданного количества контейнеров N определить количество возможных типов безопасных стопок.

Решение

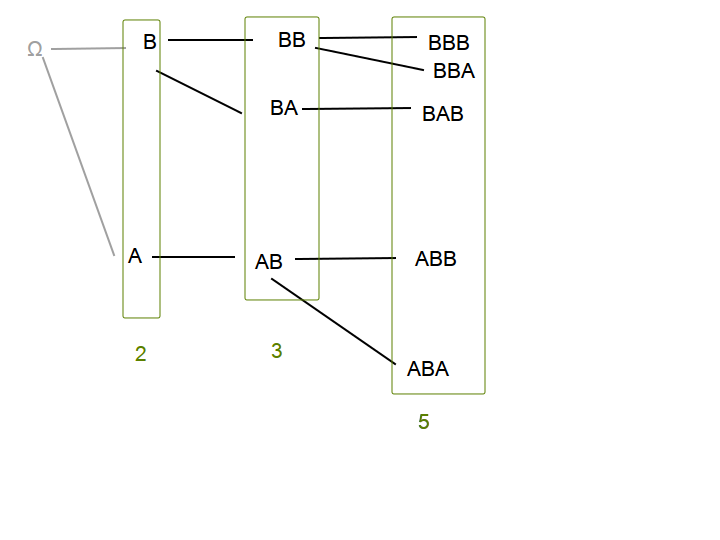
Ответом является (N+1)-е число Фибоначчи. Догадаться можно было, просто вычислив 2-3 первых значения. Строго доказать можно было, построив дерево возможных построений.

Каждый основной элемент делится на два — основной (заканчивается на B) и побочный (заканчивается на A). Побочные элементы превращаются в основные за одну итерацию (к последовательности, заканчивающейся на A, можно дописать только B). Это характерно для чисел Фибоначчи.

Реализация

Подъём по лестнице

Мальчик подошел к платной лестнице. Чтобы наступить на любую ступеньку, нужно заплатить указанную на ней сумму. Мальчик умеет перешагивать на следующую ступеньку, либо перепрыгивать через ступеньку. Требуется узнать, какая наименьшая сумма понадобится мальчику, чтобы добраться до верхней ступеньки.

Решение

Очевидно, что сумма, которую мальчик отдаст на N-ой ступеньке, есть сумма, которую он отдал до этого плюс стоимость самой ступеньки. «Сумма, которую он отдал до этого» зависит от того, с какой ступеньки мальчик шагает на N-ую — с (N-1)-й или с (N-2)-й. Выбирать нужно наименьшую.

Реализация

Калькулятор

Имеется калькулятор, который выполняет три операции:

Определите, какое наименьшее число операций необходимо для того, чтобы получить из числа 1 заданное число N. Выведите это число, и, на следующей строке, набор исполненных операций вида «111231».

Решение

Наивное решение состоит в том, чтобы делить число на 3, пока это возможно, иначе на 2, если это возможно, иначе вычитать единицу, и так до тех пор, пока оно не обратится в единицу. Это неверное решение, т.к. оно исключает, например, возможность убавить число на единицу, а затем разделить на три, из-за чего на больших числах (например, 32718) возникают ошибки.

Правильное решение заключается в нахождении для каждого числа от 2 до N минимального количества действий на основе предыдущих элементов, иначе говоря: F(N) = min(F(N-1), F(N/2), F(N/3)) + 1. Следует помнить, что все индексы должны быть целыми.

Для воссоздания списка действий необходимо идти в обратном направлении и искать такой индекс i, что F(i)=F(N), где N — номер рассматриваемого элемента. Если i=N-1, записываем в начало строки 1, если i=N/2 — двойку, иначе — тройку.

Реализация

Самый дешёвый путь

В каждой клетке прямоугольной таблицы N*M записано некоторое число. Изначально игрок находится в левой верхней клетке. За один ход ему разрешается перемещаться в соседнюю клетку либо вправо, либо вниз (влево и вверх перемещаться запрещено). При проходе через клетку с игрока берут столько килограммов еды, какое число записано в этой клетке (еду берут также за первую и последнюю клетки его пути).

Требуется найти минимальный вес еды в килограммах, отдав которую игрок может попасть в правый нижний угол.

Решение

В любую клетку таблицы мы можем попасть либо из клетки, находящейся непосредственно над ней, либо из клетки, находящейся непосредственно слева. Таким образом, F(x,y) = min(F(x-1,y), F(x,y-1)). Чтобы не обрабатывать граничные случаи, можно добавить первую строку и столбец, заполненные некоторой константой — каким-то числом, заведомо большим содержимого любой из клеток.

Источник

Что такое динамическое программирование — объясняют эксперты

Время от времени в разных статьях упоминается динамическое программирование, которое начинающий программист может спутать с чем-нибудь вроде объектно-ориентированного программирования. Мы попросили экспертов простым языком объяснить, что такое динамическое программирование.

технический директор iD EAST

Динамическое программирование — достаточно широко используемый подход к решению задач, основанный на идее «разделяй и властвуй». Достаточно часто невозможно или крайне затруднительно создать некий общий алгоритм решения проблемы, который бы брал входные данные, что-то с ними делал и сразу выдавал ответ.

Часто способа решить задачу методом «делай раз, делай два, делай три» не существует. Но всегда можно разделить большую задачу на множество маленьких и дробить так до тех пор, пока упрощённые задачи не станут примитивно простыми. Это подход, известный как «разделяй и властвуй». Довольно часто для этого используется рекурсия — вызов функцией самой себя.

Важная особенность чтобы этот процесс не зациклился нужно чтобы на каком-то этапе задача сводилась к примитивному случаю, ответ на который известен сразу. Пример — вычисление факториала числа. Такую задачу можно решить и с помощью простого алгоритма n!=1·2·3·…·n, в этом случае можно сразу получить значение (например 4! = 1·2·3·4 = 24, а 5! = 1·2·3·4·5 = 120). Но эту же задачу можно решить и рекурсивно, ведь 5! = 5·4!, а 4! = 4·3! и так далее. Значит можно написать простую функцию расчета факториала n!, которая будет умножать число на результат вызова самой себя для более простого случая (n-1)!. И только в примитивном случае 1! функция вызывать саму себя не будет, а сразу вернёт 1, это важный момент, чтобы не возникло зацикливания.

Но «разделяй и властвуй» — это ещё не совсем динамическое программирование, так как такой подход хоть и прост, но часто приводит к лавинообразному росту необходимых вычислений, хоть сам метод может быть сколь угодно простым.

Взять, к примеру, задачу поиска кратчайшего маршрута по городу из точки А в точку Б. На практике такие задачи решаются с использованием теории графов, когда каждой улице в городе ставится в соответствие ребро графа, а каждой возможной точке пребывания — узел графа. Каждому ребру приписывается некоторая условная «стоимость», соответствующая, например времени прохождения или даже непосредственно денежная стоимости проезда по соответствующей «улице». Эта стоимость в реальности может даже меняться с течением времени, например из-за пробок. Тогда необходима функция, находящая кратчайший маршрут — такую последовательность узлов, пройдя через которые мы получим минимальную «стоимость» прохождения всех соединяющих их рёбер.

И вот для таких задач методы динамического программирования становится практически единственными рабочими вариантами решения. Методы рекурсии здесь уже не подойдут: можно, конечно, решить эту задачу и таким образом: написать функцию, возвращающую стоимость ухода из точки А по каждой из возможных «улиц», каждая из этих функций в свою очередь добавит к ней стоимость участка до следующего «перекрёстка», вызвав саму себя еще раз, и повторит это многократно, пока в результате не «дойдёт» до точки Б. По итогу, среди всех цепочек ответов можно будет выбрать ту, стоимость которой минимальна и получить ответ на задачу. Но на практике сделать такое возможно только для очень простых графов с десятками узлов, например для карты метро. А вот уже в масштабах карты улиц города подобные алгоритмы становятся нереалистичными.

тимлид в ADCI Solutions

Если вкратце, то динамическое программирование — это способ решить задачу, разбив её на мелкие задачи и скомбинировав их решения.

Обычно динамическое программирование применяют в задачах, связанных с оптимизацией, например, когда нужно найти кратчайший маршрут для перемещения из города A в город B. Либо это могут быть задачи, где нужно просчитать все возможные комбинации переходов или расположения элементов. Классический пример, в котором используется этот метод — последовательность чисел Фибоначчи.

Как видно, для решения задачек с последовательностями, нужно определить следующие условия: рекуррентная зависимость элементов последовательности друг от друга, начальное состояние. Они не всегда могут быть заданы в условии напрямую, как это было в задаче выше. Например, в видео «Динамическое программирование: траектории кузнечика» разбирают задание с количеством переходов из точки A в B.

В рассмотренных выше случаях параметром состояния было одно число, однако существуют и более сложные, многомерные классы задач. Для многомерной динамики параметрами состояния могут быть:

Поиск оптимального состояния динамики, переходов и порядка пересчёта (прямой или обратный) и включает в себя метод динамического программирования.

Узнать подробности о применениях этого метода и способах его оптимизации можно почти во всех в книжках по алгоритмам, например, в книге «Алгоритмы. Построение и анализ».

начальник отдела разработки прикладного ПО в компании ИВК

В теории вычислительных систем под термином «динамическое программирование» понимается способ решения сложных задач путём разбиения их на более простые подзадачи. Динамическое программирование применимо не ко всем задачам, а лишь к тем, которые обладают «оптимальной структурой». Оптимальная структура означает, что задача может быть разбита на несколько аналогичных задач меньшего размера, при этом для решения конечной задачи могут быть использованы результаты решения меньших задач. Примеры задач с оптимальной структурой — вычисление факториала числа, построение ряда чисел Фибоначчи, вычисление расстояния Левенштейна (красивое название, скрывающееся внутри всем известной задачи diff, вычисляющей разницу между двумя текстовыми файлами). Программист, не знакомый с теорией вычислительных систем, может подумать, здесь кроется какая-то сложная математика, но на самом деле речь идёт о всем хорошо знакомом подходе — рекурсии. Все знают, как вычислить факториал числа: нужно умножить это число на факториал числа, меньшего на единицу: F(n) = n*F(n-1) (для краткости опущена проверка n >= 1) — просто и изящно.

Так вот, динамическое программирование — это рекурсия с сохранением результатов вычислений. Представим, что нам постоянно нужно вычислять факториал разных чисел. Каждый раз, когда нам нужно вычислить факториал, например, числа 5, нам необходимо произвести 4 умножения — 5*4*3*2*1. А что, если сохранить промежуточные результаты? Допустим, мы когда-то раньше вычислили 4! = 24. Значит, нам нужно проделать только одно умножение — 5*24. А в следующий раз, когда нас спросят 5!, мы вообще можем вернуть результат сразу же. Понятно, что при таком подходе растёт скорость вычислений, но и возрастает потребление памяти. Что важнее — скорость или память — вечный вопрос. Принимать решение нужно исходя из конкретных условий.

руководитель отдела программных разработок и поддержки компании «ГЭНДАЛЬФ»

Динамическое программирование – это метод, который позволяет эффективно решать многие задачи, прежде всего, задачи комбинаторной оптимизации.

Суть метода в следующем: имеющуюся задачу рекурсивно разбиваем на более маленькие подзадачи, их — на ещё меньшие и так далее. Но решаем задачи в обратном порядке: сначала маленькие (запоминаем их решение), потом переходим к задачам побольше (строим их решение на основе сохранённых решений маленьких задач) и так далее, пока не решим исходную большую задачу.

Недостаток: обычно требуется много памяти для хранения промежуточных результатов.

Lead Software Engineer в EPAM

Вычислительная сложность многих задач не зависит от входных параметров, например, получение элемента по индексу в массиве не зависит от длины массива и всегда выполняется за константное время. В то же время есть задачи, для которых время выполнения линейно зависит от значения параметров, например, получение элемента по индексу в связанном списке ― чем больше элементов, тем больше времени потребуется на поиск нужного элемента. Естественно, существуют и задачи, для которых использование полного перебора требует слишком много времени, например, поиск кратчайшего маршрута между двумя городами в случае полного перебора потребует построение n! вариантов, что при больших n неэффективно.

Некоторые подобные задачи можно решить путем разбиения исходной задачи на подзадачи меньшего размера и сложности, решив которые и объединив результаты, можно получить решение исходной задачи. Такой подход называется динамическим программированием и был предложен Ричардом Беллманом в 1940-х годах.

Динамическое программирование придерживается двух подходов к решению задач:

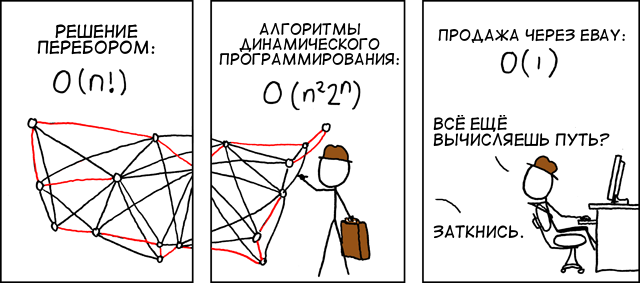
Одной из самых известных задач динамического программирования является задача вычисления чисел Фибоначчи, и она эффективно решается методом восходящего динамического программирования. При использовании этого подхода для нахождения N-го элемента в последовательности происходит последовательное нахождение первого, второго и последующих элементов как суммы двух предыдущих. Данный подход имеет сложность O(N), в то время как использование классического рекурсивного подхода имеет приблизительную сложность O(2^N), что существенно больше.

С помощью чисел Фибоначчи описываются многие явления, однако, давайте посмотрим на более практический пример ― задачу коммивояжера или, на современный лад, курьера ― курьер должен посетить N адресов, побывав на каждом из адресов ровно по одному разу и завершить свой маршрут в исходной точке. Задача заключается в нахождении маршрута минимальной длинны.

Данную задачу можно решить методом полного перебора ― сгенерировать все возможные маршруты (всего их N!) для N адресов, а затем выбрать маршрут минимальной длины. Сложность данного алгоритма O(N! * N) и время вычисления очень быстро растет при росте количества адресов ― если для трех адресов нужно рассмотреть шесть вариантов, то для 10 уже около четырех миллионов!

Использование подходов динамического программирования может не дать наилучшего решения, но, тем не менее, оно будет достаточно хорошим и за приемлемое время. Суть подхода к решению данной задачи заключается в поиске ближайшего адреса на каждом шаге ― из исходной точки, затем следующего ближайшего пункта назначения из первого адреса и так далее. Полученное решение не будет идеальным, но потребует гораздо меньше времени ― O(N^2 * 2^N), что для тех же 10 адресов 1124 вычислений.

Таким образом, мы рассмотрели основную идею динамического программирования ― разбиение сложной задачи на коллекцию более простых, которые суммарно можно решить за гораздо меньшее время.

Источник

Всё, что вы хотели знать о динамическом программировании, но боялись спросить

Я был крайне удивлён, найдя мало статей про динамическое программирование (далее просто динамика) на хабре. Мне всегда казалось, что эта парадигма довольно сильно распространена, в том числе и за пределами олимпиад по программированию. Поэтому я постараюсь закрыть этот пробел своей статьёй.

Основы

Пожалуй, лучшее описание динамики в одно предложение, которое я когда либо слышал:

Динамическое программирование — это когда у нас есть задача, которую непонятно как решать, и мы разбиваем ее на меньшие задачи, которые тоже непонятно как решать. (с) А. Кумок.

Чтобы успешно решить задачу динамикой нужно:
1) Состояние динамики: параметр(ы), однозначно задающие подзадачу.
2) Значения начальных состояний.
3) Переходы между состояниями: формула пересчёта.
4) Порядок пересчёта.
5) Положение ответа на задачу: иногда это сумма или, например, максимум из значений нескольких состояний.

Порядок пересчёта

Существует три порядка пересчёта:
1) Прямой порядок:
Состояния последовательно пересчитывается исходя из уже посчитанных.

2) Обратный порядок:
Обновляются все состояния, зависящие от текущего состояния.

3) Ленивая динамика:
Рекурсивная мемоизированная функция пересчёта динамики. Это что-то вроде поиска в глубину по ацикличному графу состояний, где рёбра — это зависимости между ними.

Элементарный пример: числа Фибоначчи. Состояние — номер числа.

Все три варианта имеют права на жизнь. Каждый из них имеет свою область применения, хотя часто пересекающуюся с другими.

Многомерная динамика

Пример одномерной динамики приведён выше, в «порядке пересчёта», так что я сразу начну с многомерной. Она отличается от одномерной, как вы уже наверно догадались, количеством измерений, то есть количеством параметров в состоянии. Классификация по этому признаку обычно строится по схеме «один-два-много» и не особо принципиальна, на самом деле.

Многомерная динамика не сильно отличается от одномерной, в чём вы можете убедиться взглянув на пару примеров:

Пример №1: Количество СМСок

Раньше, когда у телефонов были кнопки, их клавиатуры выглядели примерно так:

Требуется подсчитать, сколько различных текстовых сообщений множно написать используя не более k нажатий на такой клавиатуре.

Прямой пересчёт:
Обратный пересчёт:

При использовании обратного пересчёта всё проще: мы всегда обращаемся вперёд, так что в отрицательные элементы мы не уйдём.

5) Ответ — это сумма всех состояний.

Пример №2: Конь

4) А теперь самое интересное в этой задаче: порядок. Здесь нельзя просто взять и пройтись по строкам или по столбцам. Потому что иначе мы будем обращаться к ещё не пересчитанным состояниям при прямом порядке, и будем брать ещё недоделанные состояния при обратном подходе.

Есть два пути:
1) Придумать хороший обход.
2) Запустить ленивую динамику, пусть сама разберётся.

Если лень думать — запускаем ленивую динамику, она отлично справится с задачей.
Если не лень, то можно придумать обход наподобие такого:

Этот порядок гарантирует обработанность всех требуемых на каждом шаге клеток при прямом обходе, и обработанность текущего состояния при обратном.

Динамика и матрица переходов

Если никогда не умножали матрицы, но хотите понять этот заголовок, то стоит прочитать хотя бы вики.

А теперь, зачем всё это надо. Умножение матриц обладает свойством ассоциативности, то есть (но при этом не обладает коммутативностью, что по-моему удивительно). Это свойство даёт нам право сделать так: .

А теперь пример посерьёзнее:

Пример №3: Пилообразная последовательность

Для начала решение без матрицы перехода:

Динамика по подотрезкам

Это класс динамики, в котором состояние — это границы подотрезка какого-нибудь массива. Суть в том, чтобы подсчитать ответы для подзадач, основывающихся на всех возможных подотрезках нашего массива. Обычно перебираются они в порядке увеличения длины, и пересчёт основывается, соответственно на более коротких отрезках.

Пример №4: Запаковка строки

Вот Развернутое условие. Я вкратце его перескажу:

Необходимо по строке s узнать длину самой короткой сжатой строки, разжимающийся в неё.

Решается эта задача, как вы уже наверняка догадались, динамикой по подотрезкам.

1) Состояние динамики: d[l][r] — сжатая строка минимальной длины, разжимающаяся в строку s[l:r]
2) Начальные состояния: все подстроки длины один можно сжать только в них самих.
3) Пересчёт динамики:
У лучшего ответа есть какая-то последняя операция сжатия: либо это просто строка из заглавных букв, или это конкатенация двух строк, или само сжатие. Так давайте переберём все варианты и выберем лучший.

Пример №5: Дубы

Динамика по поддеревьям

Параметром состояния динамики по поддеревьям обычно бывает вершина, обозначающая поддерево, в котором эта вершина — корень. Для получения значения текущего состояния обычно нужно знать результаты всех своих детей. Чаще всего реализуют лениво — просто пишут поиск в глубину из корня дерева.

Пример №6: Логическое дерево

Требуется найти минимальное количество изменений логических операций во внутренних вершинах, такое, чтобы изменилось значение в корне или сообщить, что это невозможно.

Динамика по подмножествам

В динамике по подмножествам обычно в состояние входит маска заданного множества. Перебираются чаще всего в порядке увеличения количества единиц в этой маске и пересчитываются, соответственно, из состояний, меньших по включению. Обычно используется ленивая динамика, чтобы специально не думать о порядке обхода, который иногда бывает не совсем тривиальным.

Пример №7: Гамильтонов цикл минимального веса, или задача коммивояжера

Динамика по профилю

Классическими задачами, решающимися динамикой по профилю, являются задачи на замощение поля какими-нибудь фигурами. Причём спрашиваться могут разные вещи, например, количество способов замощения или замощение минимальным количеством фигур.

Профиль — это k (зачастую один) столбцов, являющиеся границей между уже замощённой частью и ещё не замощённой. Эта граница заполнена только частично. Очень часто является частью состояния динамики.

Почти всегда состояние — это профиль и то, где этот профиль. А переход увеличивает это местоположение на один. Узнать, можно ли перейти из одного профиля в другой можно за линейное от размера профиля время. Это можно проверять каждый раз во время пересчёта, но можно и предподсчитать. Предподсчитывать будем двумерный массив can[mask][next_mask] — можно ли от одной маски перейти к другой, положив несколько фигурок, увеличив положение профиля на один. Если предподсчитывать, то времени на выполнение потребуется меньше, а памяти — больше.

Пример №8: Замощение доминошками

Здесь профиль — это один столбец. Хранить его удобно в виде двоичной маски: 0 — не замощенная клетка столбца, 1 — замощенная. То есть всего профилей .

0) Предподсчёт (опционально): перебрать все пары профилей и проверить, что из одного можно перейти в другой. В этой задаче это проверяется так:

Примеры переходов (из верхнего профиля можно перейти в нижние и только в них):

Полученная асимптотика — .

Динамика по изломанному профилю

Это очень сильная оптимизация динамики по профилю. Здесь профиль — это не только маска, но ещё и место излома. Выглядит это так:

Теперь, после добавления излома в профиль, можно переходить к следующему состоянию, добавляя всего одну фигурку, накрывающую левую клетку излома. То есть увеличением числа состояний в N раз (надо помнить, где место излома) мы сократили число переходов из одного состояния в другое с до . Асимптотика улучшилась с до .

Переходы в динамике по изломанному профилю на примере задачи про замощение доминошками (пример №8):

Восстановление ответа

Иногда бывает, что просто знать какую-то характеристику лучшего ответа недостаточно. Например, в задаче «Запаковка строки» (пример №4) мы в итоге получаем только длину самой короткой сжатой строки, но, скорее всего, нам нужна не её длина, а сама строка. В таком случае надо восстановить ответ.

В каждой задаче свой способ восстановления ответа, но самые распространенные:

Небольшие оптимизации

Память

Зачастую в динамике можно встретить задачу, в которой состояние требует быть посчитанными не очень большое количество других состояний. Например, при подсчёте чисел Фибоначчи мы используем только два последних, а к предыдущим уже никогда не обратимся. Значит, можно про них забыть, то есть не хранить в памяти. Иногда это улучшает асимптотическую оценку по памяти. Этим приёмом можно воспользоваться в примерах №1, №2, №3 (в решении без матрицы перехода), №7 и №8. Правда, этим никак не получится воспользоваться, если порядок обхода — ленивая динамика.

Время

Иногда бывает так, что можно улучшить асимптотическое время, используя какую-нибудь структуру данных. К примеру, в алгоритме Дейкстры можно воспользоваться очередью с приоритетами для изменения асимптотического времени.

Замена состояния

В решениях динамикой обязательно фигурирует состояние — параметры, однозначно задающие подзадачу, но это состояние не обязательно одно единственное. Иногда можно придумать другие параметры и получить с этого выгоду в виде снижения асимптотического времени или памяти.

Пример №9: Разложение числа

Решение №1:

Решение №2:

Строки здесь обозначают слагаемые.

Первое решение последовательно добавляет по одной строчке внизу таблицы, а второе — по одному столбцу слева таблицы. Вариантов размера следующей строчки много — главное, чтобы она была больше предыдущей, а столбцов — только два: такой же как предыдущий и на единичку больше.

Заключение

Основным источником была голова, а туда информация попала с лекций в Летней Компьютерной Школе (для школьников), а также кружка Андрея Станкевича и спецкурса Михаила Дворкина (darnley).

Спасибо за внимание, надеюсь эта статья кому-нибудь пригодится! Хотя мне уже пригодилась — оказывается, написание статьи это хороший способ всё вспомнить.

Источник