Что такое динамическое движение
Тема 3.1. Основные понятия и аксиомы динамики
§1. Динамика точки. Основные понятия и определения.
В разделе кинематики исследовалось движение тел без учета причин, обеспечивающих это движение. Рассматривалось движение, заданное каким-либо способом и определялись траектории, скорости и ускорения точек этого тела.
В разделе динамики решается более сложная и важная задача. Определяется движение тела под действием сил приложенных к нему, с учетом внешних и внутренних условий, влияющих на это движение, включая самих материальных тел.
Динамикой называется раздел механики, в котором изучаются законы движения материальных тел под действием сил.
Понятие о силе, как о величине, характеризующей меру механического взаимодействия материальных тел, было введено в статике. Но при этом в статике мы, по существу, считали все силы постоянными. Между тем, на движущееся тело наряду с постоянными силами (постоянной, например, можно считать силу тяжести) действуют обычно силы переменные, модули и направления которых при движении тела изменяются.
Сила – векторная физическая величина, характеризующая действие одного тела на другое, в результате чего у тела изменяется скорость, то есть появляется ускорение, или происходит деформация тела, либо имеет место и то, и другое. В том случае, когда тело при взаимодействии получает ускорение, говорят о динамическом проявлении сил. В том случае, когда тело при взаимодействии деформируется, говорят о статическом проявлении сил.
Как показывает опыт, переменные силы могут определенным образом зависеть от времени, от положения тела и от его скорости. В частности, от времени зависит сила тяги электровоза при постепенном выключении или включении реостата; от положения тела зависит сила упругости пружины; от скорости движения зависят силы сопротивления среды (воды, воздуха).
К понятию об инертности тел мы приходим, сравнивая результаты действия одной и той же силы на разные материальные тела. Опыт показывает, что если одну и ту же силу приложить к двум разным, свободным от других воздействий покоящимся телам, то в общем случае по истечении одного и того же промежутка времени эти тела пройдут разные расстояния и будут иметь разные скорости.
Инертность и представляет собой свойство материальных тел быстрее или медленнее изменять скорость своего движения под действием приложенных сил. Если, например, при действии одинаковых сил изменение скорости первого тела происходит медленнее, чем второго, то говорят, что первое тело является более инертным, и наоборот.
Количественной мерой инертности данного тела является физическая величина, называемая массой тела. В механике масса т рассматривается как величина скалярная, положительная и постоянная для каждого данного тела.
За единицу массы принят эталон – сплав платины и иридия, хранящийся в палате мер и весов в Париже: [m]=кг. Масса–величина аддитивная
и скалярная.
В общем случае движение тела зависит не только от его суммарной массы и приложенных сил; характер движения может еще зависеть от формы тела, точнее от взаимного расположения образующих его частиц (т.е. от распределения масс).
Под материальной точкой понимают материальное тело столь малых размеров, что различием в движении отдельных его точек можно пренебречь и положение которого можно определить координатами одной из его точек.
Практически данное тело можно рассматривать как материальную точку в тех случаях, когда расстояния, проходимые точками тела при его движении, очень велики по сравнению с размерами самого тела. Кроме того, как будет показано в динамике системы поступательно движущееся тело можно всегда рассматривать как материальную точку с массой, равной массе всего тела.
Наконец, материальными точками можно считать частицы, на которые мы будем мысленно разбивать любое тело при определении тех или иных его динамических характеристик.
Точку будем называть изолированной, если на точку не оказывается никакого влияния, никакого действия со стороны других тел и среды, в которой точка движется. Конечно, трудно привести пример подобного состояния. Но представить такое можно.
При вращательном движении тела точки могут двигаться неодинаково, в этом случае некоторые положения динамики можно применять только к отдельным точкам, а материальный объект рассматривать как совокупность материальных точек.
§2. Законы динамики
В основе динамики лежат законы, установленные путем обобщения результатов целого ряда опытов и наблюдений над движением тел и проверенные обширной общественно-исторической практикой человечества. Систематически эти законы были впервые изложены И. Ньютоном.
Первый закон (закон инерции), открытый Галилеем, гласит: существуют такие системы отсчета, относительно которых тело покоится или движется прямолинейно и равномерно, если на него не действуют другие тела или действие этих тел компенсировано.
или в другой формулировке
если сумма действующих на тело сил равна нулю, то тело движется равномерно и прямолинейно или находится в покое.
Движение, совершаемое точкой при отсутствии сил, называется движением по инерции.
Словари
Раздел механики, изучающий движение тел под воздействием приложенных к ним сил.
1. Движение, действие, развитие.
2. Состояние движения, ход развития какого-либо явления или процесса.
Морфология: (нет) чего? дина́мики, чему? дина́мике, (вижу) что? дина́мику, чем? дина́микой, о чём? о дина́мике
Курс динамики. | Динамика твёрдого тела.
2. Динамикой называют изменение, движение или развитие какого-либо процесса, явления, состояния и т. п.
Динамика экономического роста. | Оценить динамику общественного мнения. | Наблюдать динамику болезни.
3. Динамикой в произведении искусства называют насыщенность действием, внутренним движением.
Следить за динамикой событий в пьесе. | Его образы статичны, да и какая может быть динамика в повествовании о Вечном?
4. Динамикой песни, стиха и т. п. является сила, энергия их звучания.
Динамика стихотворения во многом определяется ритмом и размером.
1. Отдел механики, изучающий законы движения тел в зависимости от действующих на них сил (мех.).
2. Ход развития, изменения какого-нибудь явления под влиянием действующих на него сил; ант. статика во 2 знач. (научн.). Динамика социального процесса.
3. перен. Обилие движения, действия (книжн.). В пьесе много динамики.
1. Раздел механики, изучающий движение тел под действием приложенных к ним сил.
2. Ход развития, изменения какого-н. явления (книжн.). Д. общественного развития.
3. Движение, действие, развитие. В пьесе много динамики.
1) Раздел механики, изучающий движение тел под действием приложенных к ним сил.
2) книжн. Состояние движения, ход развития какого-л. явления.
Динамика численности животных.
Динамика роста инфляции.
3) перен. Движение, действие, развитие.
Видеть жизнь в динамике.
Мы вечно наталкиваемся на статику мысли, динамики же мысли не видно (Бердяев).
динами́ческий, динами́чный, аэродина́мика
Из западноевропейских языков (← греч. dynamis ‘сила’, ‘способность’).
Процесс движения, развития чего-л. и перспективы его развития;
Динамика исторических событий.
Раздел механики, изучающий законы движения тел под действием приложенных к ним сил.
Заведующий кафедрой механики был отличным специалистом в динамике.
1. Раздел механики, изучающий движение тел под действием приложенных к ним сил. Курс динамики.
2. Состояние чего-л., находящегося в движении, развитии, и перспективы его изменения (противоп.: ста́тика). Д. государственного бюджета. Д. производительности труда. Д. исторических событий. // Ход развития, движения чего-л. Д. сюжета пьесы. Д. стиха. Описать события в динамике.
3. Муз. Сила, энергия звучания.
◁ Динами́ческий; Динами́чный (см.).
1. Раздел механики, изучающий законы движения тел в зависимости от действующих на них сил.
2. Состояние движения, ход развития, изменения чего-л.
Динамика государственного бюджета. Динамика производительности труда. Динамика исторических событий.
Движение, действие, развитие.
Отсутствие динамики в романе.
3. муз. Сила звучания.
СТАТИКА И РАВНОВЕСИЕ
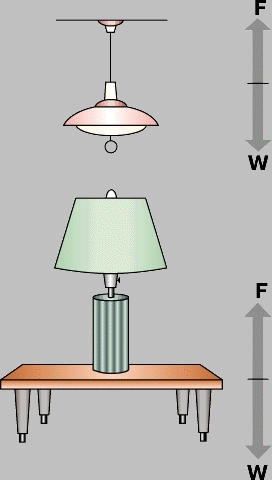
Равновесие. Тело, находящееся в состоянии покоя или равномерного и прямолинейного движения, находится в равновесии. Равнодействующая всех сил, действующих на такое тело, равна нулю. Если на тело, находящееся в равновесии, действуют только две силы, то они должны быть равны по величине и противоположны по направлению, так как только в этом случае их равнодействующая равна нулю. На рис. 1 показаны два примера тела, находящегося в равновесии в условиях, когда на него действуют две силы: лампа, стоящая на столе, и лампа, висящая на потолке. На настольную лампу действуют направленная вниз сила тяжести W, т.е. ее вес, и направленная вверх сила сопротивления стола F. Поскольку лампа находится в состоянии покоя, сила F должна быть равна по величине и противоположна по направлению силе W. Точно так же в случае висящей лампы тянущая вниз сила W должна быть равна по величине и противоположна по направлению тянущей вверх силе F натяжения шнура, на котором она подвешена.
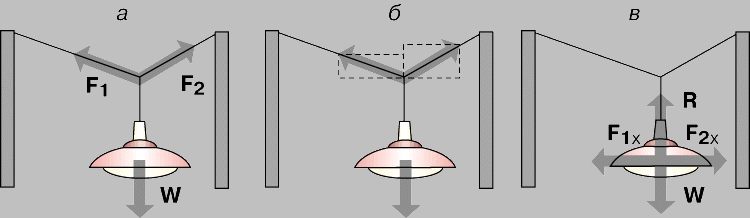
Разложение сил. Когда число сил, действующих на тело, находящееся в равновесии, больше двух, анализ несколько усложняется.
Равновесие и вращение. Во всех рассмотренных примерах равновесия действующие силы не только были равны по величине и противоположны по направлению, но и лежали на одной прямой или проходили через одну точку. Если же на твердое тело действуют силы, которые нельзя свести к одной, то они заставляют тело вращаться. (Две параллельные силы, равные по величине и противоположно направленные, называются парой сил.) Для того чтобы тело в таких условиях было в равновесии, т.е. не вращалось, пара сил должна быть уравновешена двумя такими же силами, вращающими тело в другую сторону.
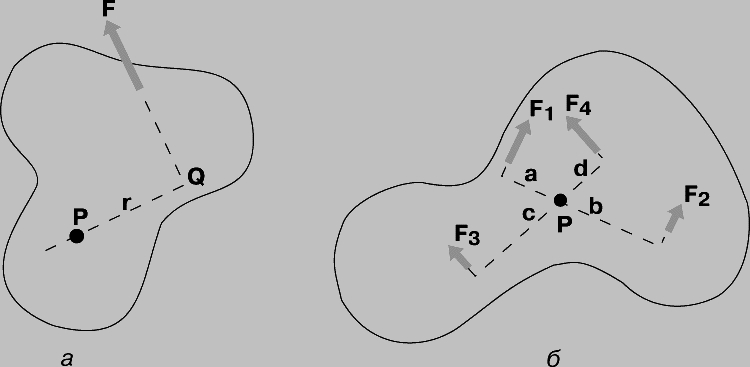
Момент силы. Если твердое тело закреплено в одной точке на шарнире и на него действует лишь одна сила, заставляющая его вращаться вокруг этой точки, то говорят, что тело вращается под действием момента силы. Момент силы равен произведению силы на ее плечо, т.е. на расстояние по перпендикуляру от точки закрепления до линии действия силы (рис. 4,а). Если на твердое тело действуют несколько сил, то тело не будет вращаться только при условии, что сумма моментов всех сил равна нулю (рис. 4,б).
Рис. 4. МОМЕНТ СИЛЫ равен произведению силы F (рис. 4,а) на плечо силы, т.е. на расстояние (по перпендикуляру) PQ от точки P шарнирного закрепления тела до линии действия силы F. В случае нескольких сил, действующих на твердое тело, способное вращаться вокруг точки P (рис. 4,б), условием равновесия является равенство нулю суммы моментов всех сил:
Равномерное движение. Тело движется равномерно, если в любую единицу времени своего движения оно проходит одно и то же расстояние в одном и том же направлении. Примером прямолинейного равномерного движения может служить движение космического аппарата, летящего по инерции в межзвездном пространстве достаточно далеко от всех небесных тел, там, где гравитационные поля ничтожно малы. Коль скоро на него не действуют никакие внешние силы, он будет, не останавливаясь, двигаться по прямой линии с постоянной скоростью. Но как только космический аппарат приблизится к какому-либо небесному телу, он окажется в гравитационном поле этого тела и начнет с нарастающей скоростью отклоняться к нему от прямолинейной траектории. Если же в межзвездном пространстве он войдет в плотное облако космической пыли, то (если отвлечься от гравитационного воздействия пыли) он по-прежнему будет двигаться прямолинейно, но с замедлением. В обоих случаях изменение характера движения вызывается действием неуравновешенных внешних сил.
Динамика изучает тела, находящиеся под воздействием неуравновешенных внешних сил, т.е. тела, характер движения которых изменяется. Поскольку равновесие означает равенство нулю равнодействующей всех сил, приложенных к телу, динамика, очевидно, имеет дело с силами, равнодействующая которых не равна нулю. Английский физик и математик И. Ньютон (1643-1727) сформулировал три закона движения, которым подчиняются тела, движущиеся под действием неуравновешенных сил, и за этими законами навсегда закрепилось его имя.
Первый закон Ньютона. Всякое тело сохраняет свое состояние покоя или равномерного и прямолинейного движения, пока неуравновешенные внешние силы не заставят его изменить это состояние. Поскольку состояние покоя, как и состояние равномерного и прямолинейного движения, соответствует равновесию, из первого закона Ньютона следует, что тело, находящееся в равновесии, остается в равновесии, пока его не выведут из этого состояния внешние силы.
Импульс (количество движения). Количеством движения тела называется произведение его массы m на его скорость v, т.е. величина mv. Количество движения одинаково у автомобиля массой 1 т, мчащегося со скоростью 100 км/ч, и у 2-тонного грузовика, едущего в том же направлении со скоростью 50 км/ч. Поскольку ускорение есть изменение скорости за малое время t, второй закон Ньютона можно переписать в виде mv = Ft. Произведение силы F на (малое) время ее действия t ранее называлось импульсом силы. Поэтому количество движения в настоящее время называют импульсом. Для импульса (количества движения) справедлив закон сохранения: при столкновении двух или нескольких тел их полный (суммарный) импульс не изменяется. Например, при забивании гвоздя молотком полный импульс молотка и гвоздя после удара равен полному импульсу молотка до удара (поскольку импульс гвоздя до удара был равен нулю).
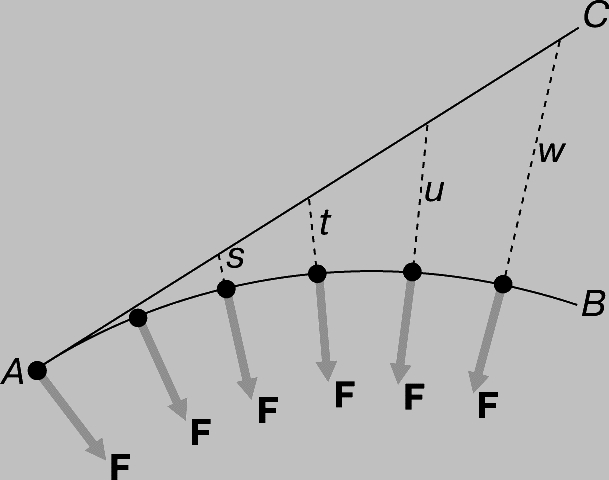
Рис. 6. УСКОРЕНИЕ, приобретаемое телом при движении по окружности. Двигаясь под действием центростремительной силы F по кривой AB, тело все больше удаляется от прямой AC (увеличиваются отклонения s, t, u, w).
Халфмэн Р. Динамика. М., 1972 Татаринов Я.В. Лекции по классической динамике. М., 1984 Ньютон И. Определения. Аксиомы и законы движения. М., 1985 Бабенков И.С. Основы статики и сопротивления материалов. М., 1988
дина́мика, дина́мики, дина́мик, дина́мике, дина́микам, дина́мику, дина́микой, дина́микою, дина́миками, дина́миках
АтлетизмИгровые виды спортаМощностьСилаСкоростьСтатьи Александра БулаховаТренировки спортсменовУскорение МАКСИМАЛЬНАЯ СИЛА И ДИНАМИЧЕСКИЕ ДВИЖЕНИЯ
Развитие максимальной силы для атлетов часто аргументируется переносом тренированности на спортивные динамические движения, такие как ускорение, бег на максимальной скорости, смену направления, прыжки и удары. В данной статье, мы рассмотрим различные аспекты, как положительные, так и отрицательные, которые влияют на перенос максимальной силы на успех в динамических движениях в спорте.
Что такое сила?
Сила (1) – энергия, воздействующая на материальные тела, а также степень интенсивности этого воздействия
Сила (2) – способность живых существ напряжением своих мышц производить физическое воздействие против различного рода сопротивления
В динамических движениях, сила мышц атлета и сила сопротивления противостоят друг другу. Сила сопротивления может быть:
— Силой тяжести атлета (F=m*g). Создает сопротивление в вертикальном направлении
— Массой атлета (m). Согласно второму закону Ньютона, большая масса требует пропорционально большей силы для его ускорения (a = F/m).
— Инерцией тела (m*v). Масса, разогнанная до скорости, обладает инерцией. Если она направлена в противоположную сторону к прилагаемой силе атлета, то атлету нужно сначала погасить инерцию тела, прежде чем оно будет двигаться в сторону прилагаемой им силы.
— Силой трения (m*g*µ). Трение возникает при контакте частей тела атлета с опорой.
— Силой сопротивления воздуха
— Силой, проявляемой соперником
— Комбинацией вышеуказанных сил
Кривая силы сокращения мышц
При начале сокращения мышцы, выдаваемая сила равна нулю. В течении определенного времени, сила нарастает по кривой, достигая определенного максимального значения. При отсутствии внешних факторов, достигается максимальная сила сокращения. Время, необходимое мышце на достижение максимальной силы в данной задаче, называется временем достижения максимальной силы.
Импульс
Рассмотрим типичную кривую силы, проявляемую атлетом против внешней нагрузки (вес собственного тела). Вначале сокращения, мышцы начинают проявлять силу с нуля. До тех пор, пока проявляемая сила не стала выше силы сопротивления, движение не происходит – это изометрическая фаза: рост напряжения мышц без движения.
Когда проявляемая атлетом сила становится больше силы сопротивления (точка А), вес начинает перемещение. После того, как проявляемая сила становится меньше силы сопротивления (точка Б), вес перестает ускоряться, и начинает замедляться под действием силы тяжести, силы трения или силы сопротивления воздуха/соперника.
Серая площадь называется импульсом – количеством произведенной силы за момент времени.
Скорость объекта на момент прекращения передачи ему силы может быть выражена, в общем случае, соотношением «импульс-момент»:
Поскольку скорость – это определяющая величина успеха в динамических движениях, мы можем сделать вывод, что для динамических движений важен результирующий импульс – количество силы сверх внешней нагрузки за период времени проявления силы.
Максимальная сила – кривая «сила-скорость»
Для понимания важности максимальной силы в динамических движениях, нужно иметь представление о кривой «сила-скорость».
Эта кривая является отражением физиологических свойств мышц – от единичных актин-миозиновых мостиков, до миофибрилл, и до целых мышц, мышечных групп и комплексных движений.
Кривая «сила-скорость» показывает, что в единичном концентрическом сокращении (при уменьшении длины мышечного волокна) достижение максимальной проявляемой силы возможно при небольшой скорости перемещения нагрузки. Достижение максимальной скорости сокращения, наоборот, требует минимальной внешней нагрузки, относительно изометрического максимума силы, и приводит к меньшей выдаваемой силе.
На первый взгляд, кажется, что это показывает противоположность силы и скорости. Но возьмем простой пример: рост показателя в вертикальном прыжке. Масса атлета составляет 80 кг, а его вес (сила тяжести) будет равна 80*9,81=785 Н сопротивления.
Поскольку вертикальный прыжок зависит от конечной вертикальной скорости при отталкивании, встает вопрос – как увеличить вертикальную скорость отрыва атлета, с учетом кривой «сила-скорость»?
Конечно, мы можем попытаться уменьшить массу атлета (силу тяжести). Но этот способ достаточно быстро исчерпает себя. Другой вариант – повышение изометрического максимума силы. В этом случае, масса атлета, как сопротивление движению, не меняется, но меняется процент нагрузки.
Итак, наш атлет имеет массу тела в 80 кг. В начале своих тренировок, атлет имеет 1 ПМ в приседаниях (максимальный вес, который атлет может поднять в одном повторении), равный 80 кг. Проявляемая сила считается как сумма силы тяжести штанги и 85% силы тяжести тела, поскольку вес этой части тела (без учета голеней и стоп) также участвует в сопротивлении. Мы получаем 1452 Н.
Стоит отметить, что 1 ПМ в приседаниях не равняется изометрическому максимуму силы, поскольку движение происходит с некоторой скоростью (0,22+-0.05 м/с). Истинный изометрический максимум будет в среднем на 10.9% выше. Но мы упустим этот момент, поскольку в обычных условиях, намного проще произвести тест 1 ПМ, чем выполнить замер изометрической силы
Если мы отнесем вес атлета к его динамической силе в 1 ПМ приседе, то получим 54%. Именно такой процент от максимальных силовых возможностей преодолевает атлет с данными параметрами во время прыжка.
При повышении силовых возможностей в 1 ПМ приседаниях (120 кг, 160 кг, 200 кг и 240 кг), процент нагрузки падает.
Таким образом, мы делаем движение легче (и быстрее) не за счет облегчения нагрузки, а за счет роста максимума силы. Теперь, относительного растущего максимума силы, та же внешняя нагрузка будет все меньше и меньше, что (должно) привести к росту скорости отрыва, и увеличению вертикального прыжка.
Из-за того, что вертикальный прыжок требует преодоления силы тяжести тела, которая может составлять даже у продвинутых атлетов 25-30% от максимальной силы, связь между относительной силой (Н/кг веса тела) и высотой вертикального прыжка сильнее, чем между высотой вертикального прыжка и максимальной скоростью сокращения мышечных волокон.
Сила за лимит времени
Однако, динамические движения отличает лимит времени – ограниченное время на проявление силы в данном движении.
Представьте себе выпрыгивание из нижней точки. Вертикальная скорость внизу равна нулю. При отталкивании, тело атлета разгоняется до пиковой скорости. При постоянной амплитуде движения, для роста пиковой скорости атлету нужно будет все быстрее и быстрее отталкиваться (выполнять движение быстрее, а значит, за меньшее количество времени).
Как было уже показано выше, сила нарастает с нуля постепенно. Если мы возьмем движение, где имеется определенный лимит времени, то атлет Б, имеющий большую максимальную силу, может оказаться хуже, чем атлет А. Все потому, что кривая силы у атлета А идет более круто, и в итоге, в данном движении с данным лимитом времени, он оказывается сильнее.
То, сколько силы успеет проявить атлет за лимит времени в динамическом движении, зависит от такого качества, как скорость нарастания силы (СНС) – отношения приращения скорости ко времени, за которое произошло это приращение силы.
СНС может считаться как для начала сокращения до какого-либо момента времени (отрыва), так и изолированно, для любого выбранного промежутка времени. Например, СНС (100-200) означает, что данный параметр был рассчитан в промежутке от 100 мс до 200 мс с начала сокращения.
Важность СНС в динамических движениях
Вернемся к атлету с массой тела в 80 кг, который хочет увеличить свой вертикальный прыжок. Допустим, что амплитуда его прыжка составляет 0,45 м. Рассчитаем скорость отрыва ЦМТ, время отталкивания, импульс, пиковую силу и СНС для вертикального отрыва ЦМТ от 0,3 м до 1,2 м.
Мы предполагаем, что в момент начала отталкивания атлет воздействует на опору с силой, равной силе тяжести тела. Затем, первую половину времени отталкивания происходит повышение силы, и вторую половину времени отталкивания, сила падает до нуля вследствие отрыва.
Итого, конечные данные расчетов выглядят следующим образом:
Вертикальный отрыв ЦМТ увеличился с 0,3 м до 1,2 м (в 4 раза). При этом, вертикальная скорость выросла лишь в 2 раза, из-за квадратичной зависимости от высоты отрыва. Во столько же раз вырос результирующий импульс, и упало время отталкивания. Пиковая сила, при этом, выросла в 2,7 раза, а необходимая СНС – в целых 8 раз!
Возрастающая роль СНС объясняется тем, что для большей вертикальной скорости отрыва нужен больший результирующий импульс. Поскольку время отталкивания вследствие роста скорости также падает, это приводит к необходимости проявления больших сил. Последнее, из-за все того же падения времени отталкивания (более жесткий лимит времени) требует значительно больших показателей СНС.
Рост СНС при различном стиле силовых тренировок
СНС может увеличиваться вследствие использования различного рода нагрузок. Однако то, на каком участке рост СНС (и силы за лимит времени) будет более выраженным, зависит непосредственно от стиля тренировок.
В общем, СНС растет и от тяжелых силовых тренировок, и от взрывного баллистического тренинга (перемещение немаксимальных весов с максимальным ускорением без замедления). Однако, тяжелый тренинг лучше растит пиковую силу (без лимита времени), а баллистический – силу за 200 мс, и, соответственно, СНС:
Другие исследования показывают, что 24 недели силовых тренировок больше всего увеличили силу за период 400-500 мс, тогда как плиометрика оказала большее влияние на участок 100-300 мс. Также, плиометрика увеличила начальную крутизну кривой, чего не было замечено после силового тренинга.
Реальная кривая «сила-скорость» для приседаний/прыжков
Разобранная ранее кривая «сила-скорость» выглядит не как кривая, а как, скорее, прямая линия с определенным наклоном, для комплексных движений, типа приседаний/вертикального прыжка:
Видно, что атлет А более сильный, чем атлет Б. Но в регионе высокой скорости, разница в силе не столь заметна. Это также можно проследить по графику силы для различных % весов при выпрыгиваниях (проценты взяты от 1 ПМ каждого атлета):
Причина очевидна – при повышении скорости движения, мышцы не успевают проявить много сил: движение заканчивается намного раньше, чем может быть проявлена максимальная сила.
Также, у различных атлетов наклон прямой «сила-скорость» в движении может быть различен вследствие самых разных причин – от антропометрии и соотношения волокон до стиля тренировок и текущего физического состояния. Это называется профилем «сила-скорость» для данного атлета.
Если взять графики силы и скорости для выпрыгиваний с весами 0 кг, 20 кг, 40 кг, 60 кг и 80 кг, то обнаружится прямая зависимость между величиной нагрузки и силой, и обратная – со скоростью движения:
Адаптации силовых тренировок
Вместе с тем, силовые тренировки вызывают адаптации в организме, которые могут быть полезны для роста результата в динамических движениях.
Во-первых, силовые тренировки увеличивают уровень рекрутирования высоко-пороговых ДЕ: те двигательные единицы, что ранее были не способы активироваться ЦНС, теперь добавляют больше силы в движении.
Во-вторых, такое качество, как частота активации ДЕ (нейронного импульса) также увеличивается: большая частота означает большую выдаваемую силу, поскольку мышечные волокна чаще напрягаются и реже расслабляются за данный промежуток времени.
И, в-третьих, рост частоты активации также увеличивает и СНС, позволяя мышцам быстрее набирать необходимую силу.
Однако, медленные силовые движения хорошо увеличивают уровни рекрутирования ДЕ, но частота импульса редко превышает 30 Гц.
Еще, влияние оказывает миофибриллярная гипертрофия, которая в теории, увеличивает проявляемую силу при любой скорости сокращения. Однако, чем быстрее движение, тем меньше актин-миозиновых мостиков будет успевать сокращаться (соотношение «сила-скорость»), и выигрыш будет все меньше.
Силовые тренировки могут увеличивать жесткость сухожилий, что является плюсом для динамических движений с рефлексом растяжение-сокращение.
Силовые тренировки увеличивают плечо силы мышцы (за счет гипертрофии), угол перистости и латеральную передачу силы, уровень активации мышц-антагонистов. Эти адаптации полезны для роста проявляемой силы в медленных движениях против тяжелой нагрузки, но негативно влияют на рост проявляемой силы в быстрых динамических движениях.
Можно сделать вывод, что силовые тренировки дают как положительные, так и отрицательные адаптации касаемо успеха в динамических движениях.
Вместо послесловия
У читателя может возникнуть вопрос: «каким образом в динамических движениях, типа вертикального прыжка, возможно проявление столь высоких сил, если при увеличении скорости сокращения сила лишь падает?»
Ответом на этот вопрос будет механизм динамических движений, который несколько отличается от концентрических и изометрических сокращений, что мы рассматривали как пример выше.
Для динамических движений характерно плиометрическое сокращение – эксцентрика, сопровождающаяся торможением с поглощением энергии пассивными элементами мышц и сухожилий, а также вызывающей рефлекс растяжения – механизм обратной связи ЦНС на растяжение мышечного волокна.
Это совместные действия помогают проявлять атлету большие силы, даже при условии жесткого лимита времени. Но об этом в следующий раз.