Что такое динамический процесс

Динамический процесс

Динамический процесс

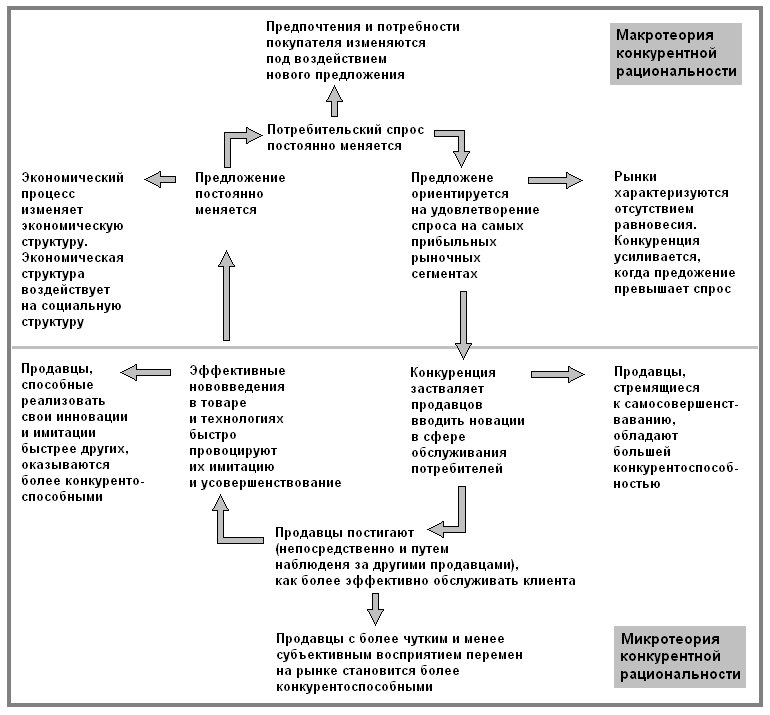
Рис. 1-2. Макро- и микротеория конкурентной рациональности

Верхняя половина рисунка описывает рыночную ситуацию на макроуровне; нижняя — на микроуровне, уровне конкретной фирмы. Логические выводы и следствия теоретических положений выделены курсивом. Каждое положение служит базисом для следующего. Например, постоянные изменения в предложении влекут за собой изменение спроса, что, в свою очередь, приводит к его переориентации на удовлетворение запросов более прибыльных рыночных сегментов. Это порождает стремление поиска пути более качественного обслуживания сегмента. Последнее предполагает продолжение исследования, что приводит к более эффективной и быстрой имитации, порождающей постоянное изменение в предложении. В отличие от большинства других теорий, конкурентная рациональность не имеет исходного набора предпосылок, на которые опираются все другие положения. Вместо этого каждое положение служит предпосылкой для следующего положения. Это дает ответ на вопрос, почему на представленной схеме нет отправной точки. Это также служит объяснением того, почему конкурентная рациональность является динамичной теорией бесконечных циклов инноваций-имитаций форм товара, каналов распределения и рыночных типов поведения, постоянно направленной на повышение эффективности и результативности.

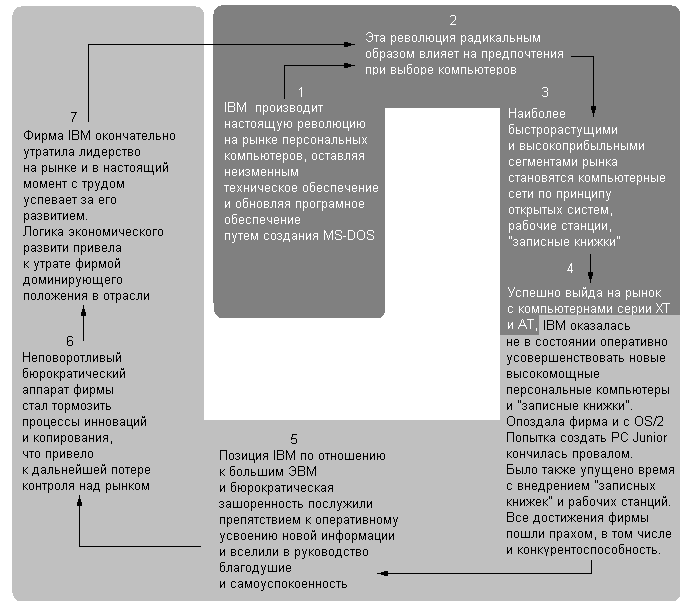
На рисунке показано, как имевшая оглушительный успех конкурентная рациональность фирмы IBM на начальной стадии сменилась конкурентной неудачей. Почему дела фирмы пошатнулись, до сих пор неясно, но многое объясняется внутрифирменным сопротивлением развитию сверхмощных сетевых персональных компьютеров, которое создало угрозу высокоприбыльному производству больших и средних ЭВМ. В 1992 г., после безуспешных попыток реорганизации, IBM объявила о своих планах разделиться на несколько компаний. Независимая компания IBM PC, вступив в стратегический альянс с такими компаниями, как Apple, в принципе, может вновь стать сильным инноватором-имитатором, вероятно, за счет других компаний IBM, реализующих более традиционные компьютеры. Продолжение следует.

Существует гипотеза, согласно которой развитие свободных рынков осуществляется посредством процесса инновации-имитации, который сначала ускоряется, затем резко замедляется и нарастает вновь. Таким образом, товарные рынки проходят в своем развитии не один, а несколько циклов. Маркетологи описали жизненный цикл (физического) товара, который представлен этапами внедрения, роста, зрелости и спада. Конкурентная рациональность — это теория жизненных циклов бесконечной инновации-имитации. В данной теории существенно то, что продавцы постоянно оказывают влияние на рыночную конъюнктуру, а последняя, в свою очередь, влияет на них. Пример из жизни «Рациональность в действии» (см. стр. 31), демонстрирует, как компания Bausch &Lomb сформировала собственную конкурентную среду. Из примера видно, как существенно может измениться рынок под воздействием улучшенного дизайна, сокращения производственных затрат, а также изменения в каналах сбыта и конкуренции. Как следствие, вы будете также иметь иное отношение потребителей, перемену в общественном мнении; вы сможете наголову разбить конкурентов или приобрести новых, открыть новые каналы сбыта и даже изменить законы.

Читайте также

Глава 31 Динамический баланс

Глава 31 Динамический баланс Разработка категорий расходов и доходов началась с очень простой мысли: оплату услуг нельзя считать убытком. После того как понятия доходов и расходов были осмыслены, это стало более чем очевидным.Предприятие понесло расходы, пускай они и не

Инвестиционный процесс

Инвестиционный процесс Что включает в себя понятие «инвестиционный процесс»? Я разделяю его на четыре основных этапа:1. Подготовка проекта к рассмотрению.2. Рассмотрение проекта и принятие решения по нему.3. Реализация и текущий мониторинг внедрения проекта.4. Анализ

15.1.5. Поток денежных средств и динамический финансовый баланс

15.1.5. Поток денежных средств и динамический финансовый баланс Переменные, нанесенные в предыдущей диаграмме, являются главными, определяющими динамическую характеристику системы, хотя обычно финансовым переменным уделяется больше внимания. Финансовые данные,

ПРОЦЕСС НАУЧЕНИЯ

ПРОЦЕСС НАУЧЕНИЯ Огромное количество ведущих авторитетов в области научения в организациях (Хани, 1998) заявляют, что «научение имеет комплексный и разнообразный характер; оно включает в себя такие вещи, как знания, навыки, инсайты, верования, ценности, установки и

2. Процесс

2. Процесс Одной из составляющих «процесса» служит эффективная коммуникация. Чтобы успешно управлять, нужно понимать, что говорят другие (и о чем они умалчивают), и уметь четко выражать собственные мысли. Иными словами, хороший менеджер должен уметь изъясняться на всех

Процесс НПП

Процесс НПП Процесс НПП работает, потому что основан на кинетике поведения. В центре кинетики поведения находится необходимость иметь все данные о поведении. Пока вы не можете точно определить в терминах наблюдения и измерения, что люди делают сейчас и что, на ваш взгляд,

Процесс

Процесс P: Уделяйте внимание не только решению, но и процессу. Правильное решение, принятое неправильными методами, в долгосрочной перспективе хуже, чем ошибочное решение, принятое правильными методами.A: Зная, каких затрат требует работа, оценили ли вы, во что обойдется ее

Процесс

Процесс P: Дорога в Рим не всегда ведет в Рим. Она могла изменить направление после того, как на ней установили дорожный знак. Периодически пересматривайте цель своих действий.A: Всегда есть иные пути.E: Не все дороги ведут в Рим. Вы никогда не попадете в Рим, если будете

Упрощайте процесс

Упрощайте процесс После составления перечня всех этапов внимательно его изучите, чтобы найти способ сократить их число там, где это возможно. Вы уже знаете, что исключение из процесса даже одного этапа существенно снижает его сложность и, таким образом, повышает скорость

Процесс продаж

Процесс продаж Наконец, вы должны определить процедуры, связанные с предложениями о продаже и презентациями, и ожидаемый уровень результатов деятельности торгового персонала. Эту информацию не обязательно включать в бизнес-план, составленный с целью получить внешнее

Командный процесс

Командный процесс Как уже было отмечено, одна из главных проблем при составлении бизнес-плана для занятий или конкурсов – работа в команде. Овладение динамикой совместной работы в группе (как принимать решения, распределять задания, общаться и т. д.) поможет вам

Процесс

Процесс Цель процесса – взаимодействие. Если в вашей компании трудится всего пять человек, то разрабатывать процесс не нужно, поскольку они могут просто переговорить друг с другом. В такой ситуации можно решать задачи с четким пониманием ожидаемого результата,

Можете ли вы описать инвестиционный процесс, используемый Social Entrepreneurs Fund? В чем его особенности? Иными словами, чем процесс финансирования социального проекта отличается от финансирования обычного бизнеса?

Можете ли вы описать инвестиционный процесс, используемый Social Entrepreneurs Fund? В чем его особенности? Иными словами, чем процесс финансирования социального проекта отличается от финансирования обычного бизнеса? Мы изучаем бизнес и осуществляем инвестиции почти так же, как

Источник

Динамические процессы.

Динамическим процессом является процесс изменения функционального состояния системы. Система находится в динамическом процессе тогда, когда происходит изменение числа её СФЕ, включенных в действие. Но число постоянно включенных в действие СФЕ определяет стационарное состояние системы. Следовательно, динамический процесс – это процесс перехода системы с одного стационарного уровня на другой.

Если скорость изменения внешних воздействий превышает скорость установления заданного результата действия системы, то появляются переходные процессы (мультимикроциклы, см. выше), во время которых также происходит изменение числа функционирующих СФЕ. Поэтому эти переходные процессы также являются динамическими.

Следовательно, есть два типа динамических процессов – когда система переходит с одного своего стационарного состояния (уровня) на другой из-за внешнего воздействия и когда она находится в переходном мультимикроцикле. Первый из них является целевым, а второй обусловлен несовершенством систем и является паразитным, потому что на его действия отбирается дополнительная энергия, которая была предназначена на целевые действия.

По определению данному выше, в стационарном состоянии системы функционирует некоторое определённое число СФЕ, от нуля до всех. Минимальным шагом изменения уровня функционального состояния является величина, определяемая уровнем срабатывания одной СФЕ (одним квантом действия). Следовательно, в принципе, переход с одного уровня функционального состояния на другой всегда является дискретным (квантованным), а не гладким, и эта дискретность определяется «калибром» СФЕ. Число стационарных состояний равно числу СФЕ системы. Системы с большим количеством «мелких» СФЕ будут проходить через динамические процессы более гладко и без сильных рывков, чем системы с небольшим количеством «крупных» СФЕ.

Следовательно, динамический процесс характеризуется амплитудой прироста функций системы от минимума к максимуму (минимакс системы зависит от абсолютного числа её СФЕ), дискретностью или шагом прироста функций (зависит от «калибра» или кванта единичных СФЕ) и параметрами цикличности функций (скоростью нарастания действий системы, периодом фаз цикла и т.д.). Он может быть целевым или паразитным.

Следует отметить, что стационарное состояние также является процессом, но установившимся (стационарным) процессом. В таких случаях состояние систем от цикла к циклу не меняется. Но во время каждого цикла в системе происходит очень много различных динамических процессов, потому что система сама состоит из подсистем, в каждой из которых есть свои циклы и свои процессы. Установившийся процесс сохраняет систему в одном и том же функциональном состоянии и на одном и том же стационарном уровне, потому что по определению, данному выше, если система не меняет своего функционального состояния, то она находится в стационарном состоянии.

Следовательно, установившийся процесс и стационарное состояние – это одно и то же, потому что независимо от того, находятся ли системы в стационарном состоянии или в динамическом процессе, в их подсистемах всегда могут быть какие-либо стационарные или динамические процессы. Например, даже просто рецепция рецептором «Х» является динамическим процессом.

Отсюда – нет абсолютно инертных (бездеятельных) объектов, любой объект нашего Мира тем или иным образом как-то действует. Предполагается, что полностью «бездеятельным» объект может быть при нуле градусов Кельвина (абсолютный нуль). Попытки получить абсолютно бездеятельные системы предпринимались путём замораживания тел до долей градусов Кельвина. Но заморозить тело до абсолютного нуля, видимо, не удастся, потому что всё равно тело будет двигаться в пространстве, пересекать какие-либо магнитные, гравитационные или электрические поля и как-то взаимодействовать с ними. Поэтому, вероятно, в принципе невозможно получить абсолютно бездеятельное тело.

Целостный организм представляет собой мозаику систем, находящихся или в разных стационарных состояниях, или в динамических процессах. Можно было бы возразить, что в организме вообще нет систем в стационарном состоянии, поскольку в любых его системах постоянно происходят какие-либо динамические процессы. Во время систолы давление в аорте возрастает, а во время диастолы падает, сердце постоянно работает, кровь непрерывно течёт по сосудам, и т.д.

Всё это правильно, но оценка функций системы проводится не по текущему её состоянию, а по циклам её деятельности. Поскольку в любых системах, в том числе и в организме, все процессы циклические, то критерием стационарности является неизменность интегрального состояния системы от цикла к циклу. Аорта реагирует на внешнее воздействие (на ударный выброс левого желудочка) тем, что по мере нарастания давления напряжение её стенок возрастает, и по мере его снижения – падает. Но если взять период времени больший, чем период одного кардиоцикла, то интегральное состояние аорты от кардиоцикла к кардиоциклу не меняется и является стационарным.

Источник

Что такое динамический процесс

Динамические процессы, их особенности и классификация.

В природе происходит масса процессов, и подавляющее большинство из них – процессы динамические. Это означает, что величины, которые участвуют в процессе, меняются с течением времени.

2.Способы задания динамического закона.

Оставим в стороне процессы случайные, и сосредоточимся на процессах детерминированных как более пригодных к анализу. Как уже отмечалось, в детерминированных процессах существует точная связь между временем и значениями всех величин процесса. Эта связь может быть выражена в нескольких формах.

Наиболее простой является явная форма, когда зависимость описывается функцией:

Подставив в выражение определённое значение времени мы получим значения всех интересующих нас параметров. Такая связь очень удобна и наглядна.

Однако не всегда возможно сразу записать динамический закон в явной форме. Часто мы имеем дело со случаем, когда изначально известна зависимость величин от некоторых внешних факторов и от предыдущей истории поведения процесса. Тогда на помощь приходит другой – неявный способ записи динамического закона:

Чаще всего от неявного способа записи можно перейти к явному.

Как можно заметить, вышеприведённые зависимости задают не один, а бесконечное множество процессов вида

где С – произвольная константа. Очевидно, что для однозначного определения процесса необходимо задать значение константы, что обычно делается через начальное условие – набор значений переменных процесса в определённый момент времени:

3.Способы исследования динамического закона.

Если мы имеем динамический закон в явном виде, то его анализ не представляет особого труда. В самом деле, мы имеем чёткую зависимость всех параметров процесса относительно времени, можем представить её в любой наглядной форме и способны провести любые исследования. При наличии вычислительной техники можно получить значение любого параметра с достаточно высокой точностью.

Если динамический закон задан в неявной форме, то определить значения величин в заданное время сразу же вряд ли удастся. Чаще всего в таких случаях преобразуют закон к явному виду. Но это не всегда удаётся. Если процесс нестационарный, да к тому же нелинейный, то аналитически разрешить уравнения очень трудно, а часто и вовсе невозможно. То есть мы не можем получить запись процесса в явном виде, и всё, что нам остаётся – неявная форма записи. Между тем не процесс полностью детерминирован. На помощь приходят численные методы.

Рассмотрим процесс, записанный в рекуррентной форме. Нам необходимо вычислить значение:

Так как мы имеем начальное условие:

То проделав последовательно ряд вычислений:

получим в конце значение переменной в интересующий нас момент. Аналогично обстоят дела с процессами, записанными в дифференциальной форме, с той лишь разницей, что вместо последовательных итераций используется численное интегрирование (которое, по сути, представляет собой те же итерации).

Как можно заметить, метод последовательных вычислений не зависит от вида динамического закона и может быть использован для анализа широкого круга задач. К его недостаткам можно отнести то, что результат представлен только в численном виде.

Устойчивость. Аттракторы. Границы устойчивости.

Рассмотрим динамический процесс, заданный в рекуррентной форме:

Где X – переменная процесса, С – константа, обе заданы в комплексной форме:

Если развернуть выражение, а затем приравнять отдельно действительные, отдельно – мнимые части, то процесс запишется следующим образом:

Такой процесс будем называть процессом Жюлиа. Как можно заметить, процесс является стационарным и нелинейным. Хотя многим, может быть, более удобна действительная форма записи (она, в частности, применяется при компьютерной реализации), мы в дальнейшем чаще будем применять исходную форму.

Для того, чтобы однозначно задать процесс Жюлиа, необходимо знать две величины (комплексные) – константу С и начальное значение. После этого методом последовательных вычислений (итераций) можно отследить динамику процесса и определить значение X в любой момент времени.

При рассмотрении процесса Жюлиа мы часто будем пользоваться такой характеристикой комплексного числа, как модуль или абсолютная величина, вычисляемая как квадратный корень из суммы квадратов действительной и мнимой частей:

Хоть этот процесс и кажется слишком простым, но на его примере можно рассмотреть широкий круг вопросов и промоделировать ряд интересных явлений.

Найдём равновесные (статические) точки процесса, то есть такие точки, в которых процесс становится статическим и перестаёт зависеть от времени:

Что приводит нас к необходимости решения уравнения

В простейшем случае С=0 корнями которого являются 0 и 1. При других, отличных от нуля значениях константы мы получим другие, комплексные значения равновесных точек. С уверенностью можно заметить лишь то, что их будет две, так как уравнение имеет второй порядок.

Устойчивость и аттракторы. Простейший случай.

Рассмотрим устойчивость на простейшем примере – процессе Жюлиа с нулевой константой. Как нам уже известно, равновесными точками этого процесса являются 0 и 1. Если задать начальное значение таким, что его абсолютная величина лежит между 0 и 1, то в процессе итераций точка постепенно приблизится к 0 и вскоре станет от него неотличима. Задав начальное значение с единичным модулем мы будем наблюдать следующую картину: значение переменной будет постоянно меняться, оставаясь по абсолютной величине равным 1. Если задать начальное значение по абсолютной величине больше 1, то на каждом шаге модуль числа будет увеличиваться, устремляясь в бесконечность. Таким образом, точка 0 устойчива, а область её притяжения ограничена сферой с единичным радиусом. Точка 1 неустойчива.

Устойчивость и аттракторы. Общий случай. Фракталы.

Все перечисленные особенности фрактальных объектов являются следствием того, что размерность фракталов не целая, а дробная.

При дальнейших вариациях значения константы множество Жюлиа будет претерпевать различные метаморфозы. На нём будут появляться седловые точки, оно будет разбиваться на несколько связанных участков, оно может превратиться в линию, и, наконец, при больших значениях модуля константы множество Жюлиа превращается в группу точек.

Хаотические процессы. Сценарий проникновения в хаос.

Рассмотрим простое множество Жюлиа и проследим поведение процесса со временем для различных начальных точек. Если мы стартуем с устойчивой равновесной точки, то очевидно, что мы с неё никуда не уйдём. Если взять начальное приближение далеко за границей зоны притяжения, то точка быстро устремится в бесконечность. Наибольший интерес представляет поведение процесса вблизи фрактальной границы.

Если взять начальную точку вблизи фрактальной границы и рассматривать изменения её модуля при последовательных итерациях, то можно наблюдать интересный процесс. Значения будут располагаться недалеко от границы, но они будут меняться хаотически, то есть каждый раз неповторимо. Нельзя предсказать значение точки через несколько итераций. И это при том, что сам закон итераций детерминирован!

Можно провести интересный эксперимент. Если на каком-либо шаге дать значению небольшое изменение, то поначалу это изменение не сильно скажется на последующих значениях, однако через несколько итераций структура процесса будет кардинально другой. То есть хаотический процесс является неустойчивым.

Ещё одной особенностью хаотических процессов является фрактальность их траектории. Форма различных участков с небольшими вариациями часто повторяется в разных масштабах. Существует также некоторая связь между траекторией хаотического процесса и формой границы, однако рассмотрение этого вопроса выходит за рамки данной работы.

Для анализа хаотических процессов очень удобно использовать ЭВМ. Для этого необходимо задавать начальные значения для процесса в определённом диапазоне и проводить итерационный процесс. По истечении орпеделённого числа итераций процесс останавливается. При достижении определённой верхней границы процесс считается уходящим в бесконечность, и запоминается число итераций. Если процесс был остановлен до достижения верней границы, то он либо хаотический, либо стремится к нулю.

На дисплее строится картина. Координаты точки задаются как действительная и мнимая части начального значения. Цвет точки орпеделяется числом итераций, которое ей потребовалось для достижения “потолка”. Если критическое значение не было достигнуто, то точке присваивается чёрный цвет. Таким образом, чёрным цветом будет закрашена фрактальная граница и область внутри неё, а по окрасу внешней области можно будет судить о том, насколько быстро точка приближается к бесконечности. В результате мы получим на комплексной плоскости изображение множества Жюлиа.

Можно получить изображение другого коплексного множества, носящего имя Мандельброта. Для этого необходимо менять не начальное значение, а управляющую константу процесса Жюлиа. Множество Мандельброта обладает множеством интересных свойств, но гланое заключается в его универсальности для целого множества динамических нелинейных процессов.

Рассматривая полученные изображения, можно наглядно убедиться в том, что процессы действительно имеют фрактальную границу. При увеличении проявляются всё более мелкие детали. Явно проявляется самоподобие.

Если бы мы попытались измерить длину границы, то мы получили бы бесконечность. И в то же время грацица является линией, не имеющей толщины. Единстенное объяснение подобного явления состоит в том, что фрактальные объекты имеют нецелую размерность.

Вызывает удивление эстетическая красота полученных изображений. Ещё большее удивление возникает, когда смотришь на уравнение, лежащее в основе этого изображения. Ето поистине удивительно, как в такой простой формуле может заключаться такая красота!

Мы кратко рассмотрели множество интересных явлений. Все эти явления происходят только в нелинейных процессах, потому что нелинейность подразумевает ветвление, а ветвление создаёт неустойчивость. Теоретические исследования этих явлений весьма сложны, потому что они уходят в облась нелинейных уравнений. Однако применение ЭВМ создаёт значительные удобства при исследовании. Визуализация даёт возможность быстро уловить суть явления и высказать многие идеи. И хотя такой путь не является математически строгим, скорость, с которой он приводит к результатам, потрясаем. Феномен того, что сложные явления, описываемые сухим языком формул и требующие долгого изучения опытных математиков, становятся понятными при взгляде на изображение, требует признания. Эстетика, заключённая в математических понятиях, позволяет по-новому взглянуть на взаимоотношение между “чистой наукой” и искусством, что несомненно пойдёт на пользу обеим.

Источник

ЛЕКЦИЯ № 14. Динамические процессы, протекающие в группе

Феномен групповой динамики определяется неоднозначно. М. Робер и Ф. Тельман определяли групповую динамику как процесс, посредством которого взаимодействие между конкретными индивидами уменьшает напряжение между ними или приводит их к взаимному удовлетворению.

Этот процесс объясняет принадлежность индивида к группе, привлекательность группы и членство в группе; образование стихийных или неформальных групп.

Развитие групповой динамики как направления в теории малых групп и социальной технологии связано с именем К. Левина.

Каждый член группы признает свою зависимость от других ее членов.

По определению К. Левина, «групповая динамика» – это дисциплина, исследующая положительные и отрицательные силы, которые действуют в данной группе.

При описании и объяснении принципов групповой динамики К. Левин опирался на законы гештальтпсихологии.

Если рассматривать группу как целое, то закономерности групповой динамики можно объяснить действием двух законов:

1) целое доминирует над его частями.Группа – это не просто сумма индивидов: она модифицирует поведение своих членов; извне легче повлиять на поведение всей группы, чем на поведение отдельного ее члена; каждый член признает, что он зависит от всех других членов;

2) отдельные элементы объединяются в целое.Не сходство, а взаимосвязь членов является основой для формирования группы; человек склонен становиться членом той группы, с которой он себя отождествляет, а вовсе не той, от которой он больше всего зависит.

В современном понимании групповая динамика – это развитие или движение группы во времени, обусловленное взаимодействием и взаимоотношениями членов группы между собой, а также внешним воздействием на группу.

Понятие групповой динамики включает пять основных элементов и несколько дополнительных.

Основные элементы– цели группы, нормы группы, структура группы и проблема лидерства, сплоченность группы, фазы развития группы.

Дополнительные элементы– создание подгруппы (как развитие структуры группы); отношения личности с группой.

Современные исследователи проблем групповой динамики выделяют три ее механизма: разрешение внутригрупповых противоречий, «идиосинкразический кредит» и психологический обмен.

Выражением внутригрупповых противоречий оказывается конфликт.

В теории групповой динамики он выступает в качестве интегратора новых структур.

Термин «идиосинкразический кредит» введен Е. Холландером. Этим понятием обозначается поведение, отклоняющееся от групповых норм.

«Идиосинкразический кредит» – механизм групповой динамики, когда группа дает разрешение на девиантное поведение своему лидеру или отдельным ее членам во имя достижения поставленных целей.

Девиантность поведения носит характер инновации и запускает новый механизм групповой динамики.

Малая группа может рассматриваться в трех качествах: как среда для изменения членов группы; как объект изменений; как агент изменений (когда используются организационные усилия группы).

Динамические процессы характеризуют ситуацию в группе.

Характер изменений, которые происходят в малой группе, можно проследить при рассмотрения проблем развития группы.

Идея развития группы была обозначена в психоаналитической концепции.

Толчок дан работой З. Фрейда «Групповая психология и анализ Эго».

Возникла теория развития группы Г. Шеппарда.

Она построена на осмыслении процессов, которые происходят в группах тренинга.

Идея развития группы: выделяются две фазы, на каждой из которых группа решает определенный набор проблем.

Каждая группа может по-разному реализовать общую модель развития: демонстрировать отклонения или просто распадаться в случае недостижения поставленной цели.

Соприкосновение с реальными группами заставило авторов обратить внимание на ту сторону функционирования группы, которая ранее не исследовалась.

Р. Морленд и Дж. Ливайн ввели понятие «социализация группы», при помощи которого по аналогии с процессом социализации индивида рассматривается процесс группового развития.

Критерии, на основе которых можно сравнивать различные стадии в развитии группы: оценивание(целей группы, ее положения среди других групп, значения целей для ее членов); обязательствагруппы по отношению к членам); преобразование ролей членовгруппы (большая или меньшая включенность членов группы, их идентифицированность с ней).

На основе критериев фиксируются периоды в жизни группы и соответствующие им позиции членов.

Сочетания периодов и позиций отражены в предложенной М. Чемерсом системно-процессуальной модели развития группы.

Введено понятие стадий (периодов) развития группы, которые различаются по набору критериев.

Каждая стадия связана со сменой состава группы.

Факторами смены ролей членов группы являются мера принятия группой каждого члена и принятие членом группы ее реальности.

В качестве второго блока исследований, где обозначается идея развития группы, можно назвать исследования по сравнению ориентаций личности: коллективизм–индивидуализм.

Они рассматриваются как полярные понятия.

Индивидуализм порождает специфические нормы поведения индивида в группе: ориентацию не на групповые, а на собственные цели, стремление подчеркнуть свой вклад в групповую деятельность.

Коллективизм как норматив традиционных обществ определяет взаимоотношения индивида с малой группой: позитивное отношение к целям группы, уравнительное распределение «благ» в ней, большую открытость и в общении, готовности поставить цели группы выше собственных.

Ориентации связаны с процессом развития группы: переход от одной фазы к другой в значительной степени зависит от того, какой конкретный стиль ориентации, а значит, поведения, «победит» в группе и тем самым будет способствовать или препятствовать переходу в новую фазу.

Так же, как и в первом блоке проанализированных исследований, здесь важна идея зависимости развития групп от типа общества, в котором они существуют.

ЛЕКЦИЯ № 15. Социально-психологическая сущность и содержание явлений в группах

Суть феномена давления группына индивида состоит в принятии уже существующих норм групповой жизни каждым вновь вступающим в нее индивидом.

Этот феномен получил в социальной психологии наименование феномена конформизма.

Чаще говорят не о конформизме, а о конформностиили конформном поведении, имея в виду чисто психологическую характеристику позиции индивида относительно позиции группы.

Мера конформности – мера подчинения группе в том случае, когда противопоставление мнений субъективно воспринималось индивидом как конфликт.

Различают внешнююконформность, когда мнение группы принимается индивидом лишь внешне, он продолжает ему сопротивляться, и внутреннюю(подлинный конформизм), когда индивид действительно усваивает мнение большинства.

Негативизмнаступает в случае, когда группа оказывает давление на индивида, сопротивляющегося этому давлению и демонстрирующего независимость.

Негативизм не подлинная независимость, это специфический случай конформности.

Если индивид ставит своей целью любой ценой противостоять мнению группы, то фактически вновь зависит от группы, ему приходится активно продуцировать антигрупповое поведение, т. е. быть привязанным к групповому мнению.

Конформности противопоставлены самостоятельность, независимость.

Впервые модель конформности продемонстрирована в экспериментах С. Аша, осуществленных в 1951 г.

На степень конформности влияют: менее развитый интеллект, более низкий уровень развития самосознания и т. д.

Степень конформности зависит и от таких факторов, как характер ситуации эксперимента и состав, структура группы.

Сама модель вариантов поведения, принимаемая С. Ашем, весьма упрощена, так как в ней фигурируют лишь два типа поведения: конформное и неконформное.

В реальных же ситуациях такой деятельности может возникнуть третий тип поведения.

Он будет демонстрировать сознательное признание личностьюнорм и стандартов группы.

Существуют три типа поведения:

1) внутригрупповая внушаемость, т. е. бесконфликтное принятие мнения группы;

2) конформность– осознанное внешнее согласие при внутреннем расхождении;

3) коллективизм, или коллективистическое самоопределение, – относительное единообразие поведения в результате сознательной солидарности личности с оценками и задачами коллектива.

Феномен группового давления как один из механизмов формирования малой группы (вхождения индивида в группу) неизбежно останется формальной характеристикой групповой жизни до тех пор, пока при его выявлении не будут учтены содержательные характеристики групповой деятельности, задающие особый тип отношений между членами группы.

Давление на индивида могут оказывать не только большие группы, но и меньшинство. М. Дойчем и Г. Джерардом были выделены два вида группового влияния: нормативное(давление оказывает большинство, и его мнение воспринимается членом группы как норма) и информационное(давление оказывает меньшинство, и член группы рассматривает его мнение лишь как информацию, на основе которой он должен сам осуществить свой выбор).

Групповая сплоченность– процесс формирования особого типа связей в группе, которые позволяют внешне заданную структуру превратить в психологическую общность людей, в сложный психологический организм, живущий по своим собственным законам.

Исследование проблемы групповой сплоченности опирается на понимание группы как некоторой системы межличностных отношений, имеющих эмоциональную основу.

В социометрическом направлении сплоченность прямо связывалась с таким уровнем развития межличностных отношений, когда в них высок процент выборов, основанных на взаимной симпатии.

Социометрия предложила индекс групповой сплоченности – отношение числа взаимных положительных выборов к общему числу возможных выборов.

Другой подход предложен Л. Фестингером, когда сплоченность анализировалась на основе частоты и прочности коммуникативных связей, обнаруживаемых в группе.

Сплоченность определялась как «сумма всех сил, действующих на членов группы, чтобы удерживать их в ней».

«Силы» интерпретировались либо как привлекательность группы для индивида, либо как удовлетворенность членством в группе.

Существует ряд экспериментальных работ по выявлению групповой сплоченности.

В исследованиях А. Бейвеласа особое значение придается характеру групповых целей.

Операциональные цели группы – это построение оптимальной системы коммуникаций; символические цели– цели, соответствующие индивидуальным намерениям членов группы.

Сплоченность зависит от реализации и того и другого характера целей.

Новый подход к исследованию сплоченности: процесс формирования группы и ее дальнейшего развития представлен как процесс все большего сплачивания этой группы, но не на основе увеличения лишь эмоциональной ее привлекательности, а на основе все большего включения индивидов в процесс совместной деятельности.

Совместимость членов группы означает, что данный состав группы возможен для обеспечения выполнения группой ее функций, интегрирован так, что в нем достигнута особая степень развития отношений, при которой все члены группы разделяют цели групповой деятельности.

В отечественной социальной психологии новые принципы исследования сплоченности разработаны А. В. Петровским.

Основная идея: всю структуру малой группы можно представить как состоящую из трех (в последней редакции четырех) основных слоев, страт: внешний уровень групповой структуры (непосредственные эмоциональные межличностные отношения); второй слой представляет собой более глубокое образование, «ценностно-ориентационное единство» (отношения здесь опосредованы совместной деятельностью, совпадением у членов группы ориентации на основные ценности, касающиеся процесса совместной деятельности).

Третий слой предполагает еще большее включение индивида в совместную групповую деятельность (члены группы разделяют цели групповой деятельности, и здесь могут быть выявлены наиболее серьезные, значимые мотивы выбора членами группы друг друга).

Третий слой отношений был назван «ядром» групповой структуры.

Мотивы выбора на этом уровне связаны с принятием общих ценностей.

Процесс принятия группового решения связан с проблемой лидерства и руководства, так как принятие решения – одна из важных функций руководителя.

Групповые решения во многих случаях являются более эффективными, чем индивидуальные.

Среди различных методов принятия групповых решений велика роль групповой дискуссии.

1) позволяет столкнуть противоположные позиции и тем самым помочь участникам увидеть разные стороны проблемы;

2) если решение инициировано группой, то оно является логическим выводом из дискуссии, поддержано всеми присутствующими, его значение возрастает, так как оно превращается в групповую норму.

Одна из форм групповых дискуссий, введенная А. Осборном, – «брейнсторминг»(«мозговая атака»).

Для выработки коллективного решения группа разбивается на две части: «генераторов идей» и «критиков».

Задача «генераторов идей» – набросать больше предложений относительно решения обсуждаемой проблемы.

На втором этапе «критики» начинают критиковать поступившие предложения: отсеивают непригодные, откладывают спорные, принимают удачные. Группа получает набор вариантов решения проблемы.

Другой метод групповой дискуссии, разработанный У. Гордоном, – метод синектики, соединения разнородного.

Основная идея – выработать как можно больше разнообразных и прямо противоположных, взаимоисключающих предложений.

Их задача – наиболее четко формулировать противоположные мнения.

В ходе дискуссии отбрасываются крайности, принимается решение, удовлетворяющее всех.

При исследовании вопроса о сравнительной ценности групповых и индивидуальных решений был обнаружен феномен, получивший название «сдвиг риска».

Ранее при изучении малых групп использовали тот факт, что группа отбрасывает наиболее крайние решения и принимает своего рода среднее от индивидуальных (нормализация группы).

Положение о нормализации решений отдельных членов группы не подтвердилось в случаях, когда принимаемое решение включало в себя момент риска.

Эксперимент Дж. Стоунера показал, что групповое решение включает в себя в большей мере момент риска, чем индивидуальные решения.

Преимущество группового решения перед индивидуальным зависит от уровня принятия решения: на фазе нахождения решения индивидуальное решение более продуктивно, на фазе разработки выигрывают групповые решения.

Совершенствование процесса принятия группового решения зависит от умения вести эффективную групповую дискуссию, которую развивают при помощи социально-психологического тренинга.

Из трех форм тренинга – открытое общение, ролевая игра, групповая дискуссия – последняя является одной из самых развитых.

На качество решения влияет еще один фактор, получивший название «групповой дух», – такая высокая степень включенности в систему групповых представлений и ценностей, которая мешает принятию правильного решения.

Групповая дискуссия приводит к поляризации группы.

Сущность этого явления в том, что в ходе групповой дискуссии противоположные мнения, имевшиеся у различных группировок, не только обнажаются, но и вызывают принятие или отвержение их большей частью группы.

Люди могут противостоять давлению группы и часто действительно делают это. Немногочисленные меньшинства могут упорствовать и отказываться соглашаться с окружающими.

Бывают ситуации, когда отдельные люди или группы могут меняться ролями с большинством и оказывать социальное влияние на других, а не подвергаться ему сами.

История дает нам множество тому примеров: великие ученые – Г. Галилей, Л. Пастер, З. Фрейд – сталкивались с единодушным большинством, которое резко отвергало их взгляды.

С течением времени у них появлялось все больше сторонников, пока наконец их взгляды не начинали господствовать.

Это тот случай когда меньшинству удается оказывать социальное влияние на большинство.

Данные исследований говорят о том, что больше всего шансов добиться успеха появляется в определенных условиях.

Во-первых, члены таких групп должны быть последовательными в своем противостоянии мнению большинства. Если они сомневаются или проявляют склонность к подчинению взглядам большинства, их влияние уменьшится.

Во-вторых, члены меньшинства не должны занимать жесткую и категоричную позицию. Представители меньшинства, настаивающие на своем, менее убедительны, чем те, кто демонстрирует некоторую степень уступчивости.

В-третьих, важным является общий социальный контекст, в котором действует меньшинство.

Если меньшинство утверждает позицию, согласующуюся с текущими социальными тенденциями, его шансы повлиять на большинство больше, чем если бы представители этого меньшинства утверждали позицию, которая расходится с такими тенденциями.

Даже в тех случаях, когда меньшинство является последовательным, уступчивым и его позиция согласуется с текущими социальными тенденциями, оно все равно вынуждено вести жесткую борьбу.

Власть большинства велика отчасти и потому, что в однозначных или сложных социальных ситуациях люди рассматривают большинство как источник более достоверной информации о реальности.

Одно из возможных объяснений тому, что меньшинство иногда способно заявить о себе, следующее: когда люди сталкиваются с меньшинством, взгляды которого они сначала не разделяют, у них возникает определенный интерес, они заинтригованы, им приходится прикладывать когнитивные усилия для того, чтобы понять, почему представители меньшинства занимают такую позицию и почему они столь явно не желают подчиняться широко распространенным взглядам.

Некоторые люди, сталкиваясь с мнением меньшинства, начинают уделять все больше и больше времени тщательному изучению пропагандируемых им идей.

Данные исследований Зданюка и К. Левина говорят о том, что простое предвосхищение того, что нужно оказывать влияние, будучи представителем меньшинства, оказывается достаточным, чтобы усилить мыслительные способности.

Во время реальных групповых дебатов существует возможность, что меньшинство заставит людей рассматривать идеи и их альтернативы, которые те прежде игнорировали.

Франклин Рузвельт сказал: «Никакая демократия не продержится долго, если не будет уделять достаточно внимания проблемам меньшинств».

Все динамические процессы, происходящие в малой группе, обеспечивают эффективность групповой деятельности, которая может быть исследована на различных уровнях.

Когда малая группа понимается как лабораторная группа, эффективность ее деятельности означает эффективность деятельности по выполнению конкретного задания.

В таких группах выявлены общие характеристики эффективности деятельности: зависимость эффективности от сплоченности группы, от стиля руководства, влияние на эффективность способа принятия групповых решений и т. д.

Данные исследования не изучают влияние на эффективность деятельности группы характера этой деятельности.

Проблема оборачивается сведением эффективности деятельности группы к ее продуктивности, к производительности труда в ней.

Из двух показателей эффективности – продуктивноститруда и удовлетворенностичленов группы трудом последний практически не исследован.

Результаты экспериментальных исследований противоречивы: в некоторых случаях такого рода удовлетворенность повышала эффективность деятельности группы, в других случаях – нет.

Здесь эффективность связывалась с совместной деятельностью группы, а удовлетворенность – с системой межличностных отношений.

Проблема удовлетворенности имеет другую сторону – проблему удовлетворенности трудом, т. е. выступает в непосредственном отношении к совместной групповой деятельности.

Принятие принципа совместной деятельности в качестве важнейшего интегратора группы диктует требования к изучению эффективности.

Она должна быть исследована на каждом этапе развития группы. Группы на разных стадиях развития обладают различной эффективностью при решении разнообразных задач.

На ранних этапах развития группа не в состоянии успешно решать задачи, требующие сложных навыков совместной деятельности, но ей доступны легкие задачи, которые можно разложить на составляющие.

Следующий этап развития дает больший групповой эффект, но при условии личной значимости групповой задачи для каждого участника совместной деятельности.

Если все члены группы разделяют социально значимые цели деятельности, эффективность проявляется и в том случае, когда решаемые группой задачи не приносят непосредственной личной пользы членам группы.

Возникает новый критерий успешности решения группой задачи – критерий общественной значимостизадачи.

Среди критериев групповой эффективности присутствует «сверхнормативная активность» – стремление членов группы добиваться высоких показателей сверхнеобходимого задания.

Следует учитывать обе фазы, присутствующие во всякой трудовой деятельности: подготовительную и инструментальную.

Концентрация внимания на инструментальной фазе не учитывает того, что на определенном уровне развития группы особое значение приобретает первая фаза – здесь наиболее ясно могут проявиться новые качества группы в их влиянии на каждого отдельного члена группы.

Так же, как и другие проблемы, связанные с динамическими процессами малой группы, проблема эффективности должна быть связана с идеей развития группы.

Источник