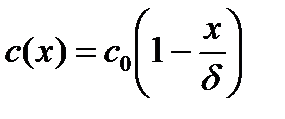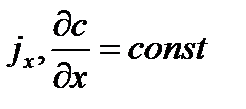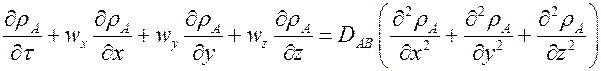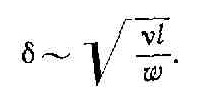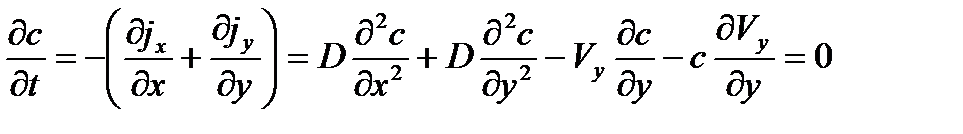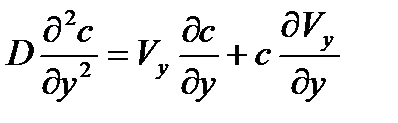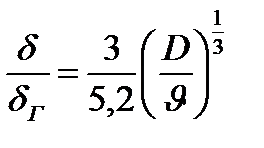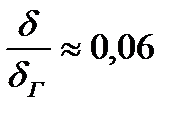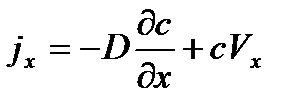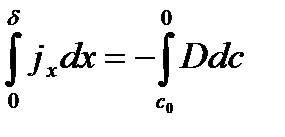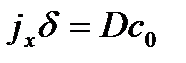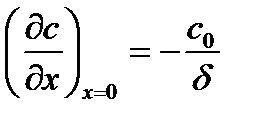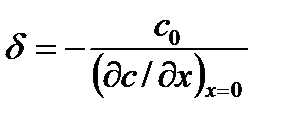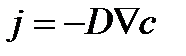Что такое диффузионный пограничный слой
Динамический, тепловой и диффузионный пограничные слои
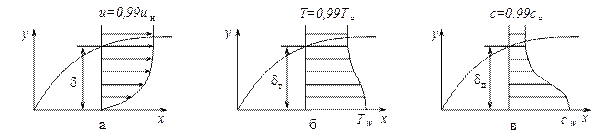
Различают динамический, тепловой и диффузионный пограничные слои на обтекаемой поверхности (рис. 3.1).
Рис. 3.1. Динамический (а), тепловой (б) и диффузионный (в) пограничные слои
Динамический пограничный слой – слой жидкости вблизи обтекаемой поверхности, поперек которого скорость меняется от скорости тела на его поверхности до скорости невозмущенного потока на границе пограничного слоя (рис. 3.1а).
При обтекании жидкостью твердого тела молекулы жидкости, находящиеся вблизи поверхности твердого тела, «прилипают» к ней под действием сил притяжения их к молекулам твердого тела (гипотеза прилипания). Прилипшие молекулы из-за вязкости жидкости взаимодействуют с близлежащими слоями, подтормаживая их. Образуется пограничный слой. Теоретически тормозящее действие слоев жидкости друг на друга может простираться по направлению нормали к поверхности в бесконечность, т.е. скорость вдоль нормали должна постепенно изменяться от u = uw = 0 при у = 0 до u = uнпри у = ∞ (индексом w будем обозначать параметры жидкости на поверхности, а индексом н – параметры невозмущенного потока). Практически же пограничный слой достаточно тонок (по сравнению с расстоянием от точки его образования до рассматриваемого сечения), так как значительное влияние прилипших молекул и, следовательно, существенное изменение скорости наблюдается лишь в непосредственной близости от поверхности твердого тела. По этой причине вводят понятие толщины пограничного слоя. За толщину динамического пограничного слоя принимается значение у, при котором скорость отличается на 1% от скорости невозмущенного потока uн, т.е. граничное условие на границе пограничного слоя записывается следующим образом: u = 0,99uнпри у=d. Кроме этого на границе пограничного слоя и за его пределами выполняется условие 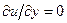
Тепловой пограничный слой – пристенный слой жидкости, поперек которого происходит существенное изменение температуры: температура жидкости меняется от температуры обтекаемой поверхности до температуры невозмущенного потока на границе слоя (рис. 3.1б).
Также как и для динамического пограничного слоя вводится толщина теплового пограничного слоя dт. За толщину теплового пограничного слоя принимается значение у, при котором температура отличается на 1% от температуры невозмущенного потока Тн. Толщина теплового пограничного слоя dт в общем случае не равна толщине динамического пограничного слоя d. Граничные условия для теплового пограничного слоя записываются следующим образом: Т = Тw при у = 0 и Т = 0,99Тн при у = dт. На границе пограничного слоя и вне его 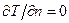
Диффузионный пограничный слой – слой жидкости вблизи обтекаемой поверхности с большим поперечным градиентом концентрации примеси 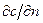
При проведении расчетов вводится толщина диффузионного пограничного слоя dд, которая равна толщине теплового пограничного слоя dт: dд= dт. Граничные условия для диффузионного пограничного слоя имеют вид: с = сw при у = 0 и с = 0,99сн при у = dд. На границе пограничного слоя и за его пределами 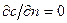
Дата добавления: 2017-03-12 ; просмотров: 3846 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
двухкомпонентной среде



По аналогии с конвективным теплообменом под конвективным массообменом понимают процесс совместного переноса массы вещества с помощью молекулярной диффузии (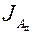
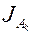
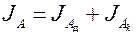
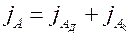
Поскольку 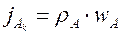
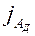
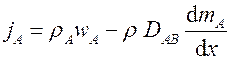
Конвективный массообмен может быть вынужденным и свободным. Если движение компонентов жидкости обусловлено разностью их плотностей, то процесс называется свободным конвективным массообменом.
Если движение компонентов жидкости вызывают внешние устройства (насос, вентилятор), процесс массообмена считается вынужденным. В качестве примера вынужденного конвективного массообмена можно назвать процесс испарения воды с поверхности водоема в ветренную погоду.
Уравнение массоотдачи. Аналогично процессу теплоотдачи конвективный массообмен между поверхностью вещества, находящегося в жидком (твердом) состоянии, и окружающей средой называют массоотдачей.
Для расчета процесса массоотдачи используется уравнение
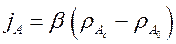
где β – коэффициент массоотдачи (м/с), который характеризует скорость переноса вещества с поверхности жидкости или твердого тела в окружающую среду.
Уравнение является основным уравнением для расчета конвективного массообмена. Это уравнение аналогично по форме записи уравнению теплоотдачи (2.2).
Дифференциальное уравнение массообмена. В записи через массовую концентрацию (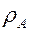
Это уравнение аналогично дифференциальному уравнению энергии массовая концентрация 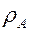
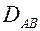
Аналогия между процессами тепло – и массообмена. Рассмотрим
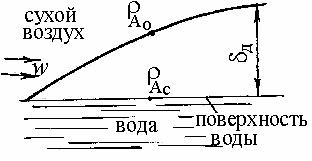
Этот пример иллюстрирует подобие между процессами конвективного теплообмена и массоообмена. Поэтому с формальной точки зрения безразлично, какую задачу решать.
Поля температур и концентраций будут различаться на постоянную величину или полностью совпадать, если критерий Льюиса-Семенова 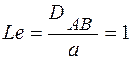
Эта аналогия предполагает, что простым методом расчета коэффициента массообмена является использование соответствующего критериального уравнения для конвективного теплообмена с подстановкой в него безразмерных комплексов, описывающих процесс массообмена.
Аналогично безразмерному числу Нуссельта, в которое входит коэффициент теплоотдачи, вводится безразмерный комплекс, описывающий массообмен, называемый числом Шервуда: 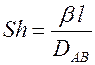
Безразмерному числу Прандтля в теории массообмена соответствует безразмерный комплекс 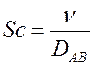
Безразмерное число Шмидта, как и безразмерный комплекс Прандтля, характеризует физические свойства среды. Безразмерное число Нуссельта при вынужденной конвекции является функцией чисел Рейнольдса и Прандтля Nu = f(Re,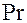
С учетом подобия между процессами конвективного тепло – и массообмена безразмерное число Шервуда будет функцией Рейнольдса и Шмидта
Например, в рассматриваемой нами задаче об испарении воды с поверхности водоема процесс массообмена аналогичен процессу теплообмена. При ламинарном режиме обтекания плоской поверхности, безразмерное число Нуссельта определяется по формуле (2.39). Такой же по виду формулой будет описываться и процесс массообмена:
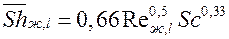
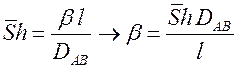
Если массоперенос осуществляется свободной конвекцией, выражение для коэффициента массообмена можно вывести на основе аналогичной задачи о теплообмене в условиях свободной конвекции.
Теплообмен при свободной конвекции описывается соотношением
Nu = f (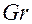
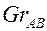
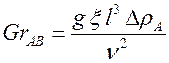
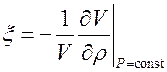
Характерной особенностью процесса массообмена по сравнению с теплообменом является наличие потока массы. Если в процессах теплообмена скорость жидкости на стенке равна нулю, то при протекании процесса массообмена 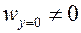
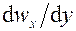
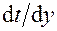
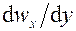
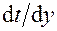
1. Исаченко В.П. Теплопередача/ В.П.Исаченко, В.А.Осипова, А.С.Сукомел. М.: Энергия, 1981. 417 с.
2. Теория тепломассообмена / С.И. Исаев [и др.]; под ред. А.И. Леонтьева. М.: Высшая школа, 1979. 495 с.
3. Кутателадзе С.С. Основы теории теплообмена/ C.С.Кутателадзе. М.: Атомиздат, 1979. 415 с.
4. Михеев М.А. Основы теплопередачи/ М.А.Михеев, И.М.Михеева. М.: Энергия, 1977. 343 с.
5. Крейт Ф. Основы теплопередачи/ Ф.Крейт, У. Блейк. М.: Мир, 1983 512 с.
6. Шлихтинг Г.Теория пограничного слоя/ Г.Шлихтинг. М.: Наука, 1974.711 7. Лыков А.В. Тепломассообмен: справочник/ А.В.Лыков. М.: Энергия, 1978. 480 с.
8. Юдаев Б.Н. Теплопередача: учебник для вузов/ Б.Н.Юдаев. 2-е изд., перераб. и доп. М.: Высшая школа, 1981. 319 с.
9. Королев В.Н. Тепломассообмен/ В.Н.Королев. Екатеринбург: УГТУ-УПИ, 2007. 279 с.
10. Тепломассообмен: приложение к лабораторным работам /Л.К.Васанова, Б.Г.Сапожников, В.Н.Королев, Ю.О.Зеленкова. Екатеринбург: УГТУ-УПИ, 2003. 32 с.
11. Справочник по теплообменным аппаратам/ П.И Бажан, Г.Е.Канавец, В.М.Селиверстов. М.: Машиностроение, 1989. 365 с.
12. Теплообменники энергетических установок: учебник для вузов/ К.Э.Аронсон [и др.]; под ред. проф., д-ра техн. наук Ю.М.Бродова. Екатеринбург: Сократ, 2002. 968 с.
Пограничный слой
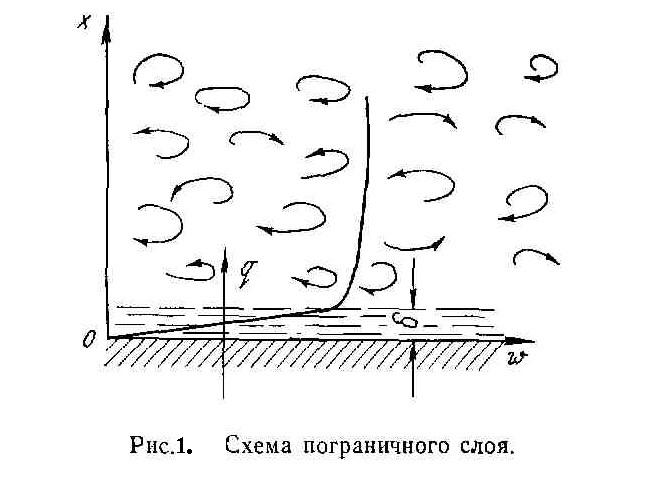
Здравствуйте, друзья! При движении жидкости возникают силы трения, особенно значительные вблизи ограничивающих течение поверхностей. Поэтому гидродинамическое взаимодействие жидкости или газа с твердым телом при условии различных скоростей их движения сопровождается образованием на границе раздела (твердая поверхность) слоя среды, движущегося со скоростью, отличной от скорости жидкости (динамический пограничный слой). Его образование всецело определяется силами вязкости.
Если поток обтекает неподвижное тело, то образуется слой заторможенной жидкости. Скорость возрастает по его толщине от нуля (на поверхности тела) до скорости потока (рис. 1).
Толщина δ пограничного слоя обычно мала по сравнению с характерным размером обтекаемого тела или поверхности δ / l
Таким образом, различают динамический, тепловой и диффузионный пограничные слои. Образуются они у поверхности, но толщина их различна. Толщина пограничного слоя — условная величина, определяемая для динамического, теплового или диффузионного пограничных слоев как расстояние по нормали от стенки, на котором основная переменная величина (продольная составляющая скорости, температура или концентрация соответственно) с заданной точностью достигает своего предельного значения вдали от стенки.
Отличаются эти пограничные слои друг от друга тем, что динамический характеризуется большим поперечным градиентом продольной составляющей скорости, тепловой— большим поперечным градиентом температуры, а диффузионный—большим градиентом концентрации водяных паров.
Толщина пограничного слоя, а также режим движения жидкости в нем играют существенную роль в теплообмене тела со средой, так как указанный слой оттесняет среду от поверхности. Между телом и средой образуется как бы промежуточное тело, которое вносит дополнительное термическое сопротивление. Режим движения в самом пограничном слое может быть как ламинарным, так и турбулентным.
Для ламинарного движения характерным является возможность существования стационарных траекторий частиц среды. При турбулентном движении траектория частиц хаотически изменяется во времени, в потоке возникают нерегулярные пульсации скорости, давления и других неравномерно распределенных параметров.
При наличии ламинарного пограничного слоя перенос теплоты через него осуществляется теплопроводностью, а так как жидкости и газы плохо проводят теплоту (коэффициент теплопроводности их невелик), то ламинарный слой является значительным термическим сопротивлением, численное значение которого прямо пропорционально его толщине.
При переходе ламинарного пограничного слоя в турбулентный это сопротивление намного уменьшается, так как перенос теплоты облегчается интенсивным перемешиванием среды внутри самого пограничного слоя. Однако даже при развитом турбулентном пограничном слое под ним всегда имеется прослойка с ламинарным режимом движения (вязкий подслой), который и оказывает в этом случае основное термическое сопротивление.
Толщина δ пограничного слоя зависит от длины тела l вдоль потока и состояния его поверхности (шероховатости), вязкости жидкости υ и скорости потока ω. Взаимосвязь между этими величинами для случая ламинарного пограничного слоя устанавливается следующим соотношением:
Согласно этому выражению, тела небольших размеров при прочих равных условиях будут иметь пограничный слой меньшей толщины, чем крупные тела. Для шара в месте минимального давления на его поверхности толщина ламинарного пограничного слоя будет равна
Уменьшение толщины пограничного слоя и, следовательно, интенсификация процесса теплообмена достигаются прежде всего увеличением скорости потока.
Существенную роль в переходе ламинарного пограничного слоя в турбулентный наряду со скоростью играет форма обтекаемого тела, а также начальная турбулентность набегающего потока. На поверхности тела с большей шероховатостью толщина образующегося пограничного слоя при прочих равных условиях будет больше. При поперечном омывании трубы или обтекании шара толщина пограничного слоя с увеличением диаметра будет возрастать, а интенсивность теплоотдачи будет уменьшаться.
Пограничный слой оказывает также влияние на процессы переноса массы. Так, например, при сушке материала, как было показано выше, над его поверхностью образуется диффузионный пограничный слой, который препятствует массообмену между поверхностью тела и газами. Перенос влаги через указанный слой осуществляется диффузией. Одновременно при этом образуется и тепловой пограничный слой. На толщину диффузионного пограничного слоя существенное влияние оказывает скорость потока. С увеличением скорости толщина слоя будет уменьшаться.
Таким образом, роль пограничного слоя в конвективном теплообмене и процессе сушки велика. В результате уменьшения его толщины, разрушения или перехода ламинарного режима в турбулентный достигается интенсификация тепло- и массообмена тела с окружающей средой. Исп.литература: 1) Теплотехника, под редакцией А.П. Баскакова, Москва, Энергоиздат, 1982. 2) Теплотехника, Бондарев В.А., Процкий А.Е., Гринкевич Р.Н. Минск, изд. 2-е,»Вышейшая школа», 1976.
Гидродинамические и диффузионные погранслои



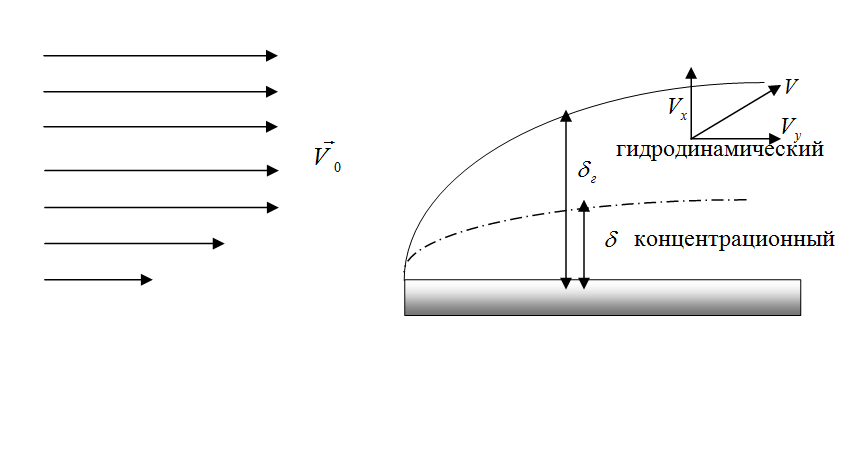
Концентрационный (диффузионный) погранслой – это та область жидкости, граничащая с твердым телом, в которой происходит изменение концентрации растворенного вещества.
Гидродинамический погранслой – это та область жидкости, в которой происходит изменение скорости течения.
При рассмотрении макроскопического течения, например, в масштабах миллиметра и более, используется условие прилипания, т е считается, что на поверхности твердого тела скорость течения равна нулю. При рассмотрении микроскопического течения данное допущение неверно.
В данном разделе изучается макроскопическое течение. Скорость изменяется от 0 на поверхности тела до некоторого значения, которое не меняется при дальнейшем удалении от поверхности.
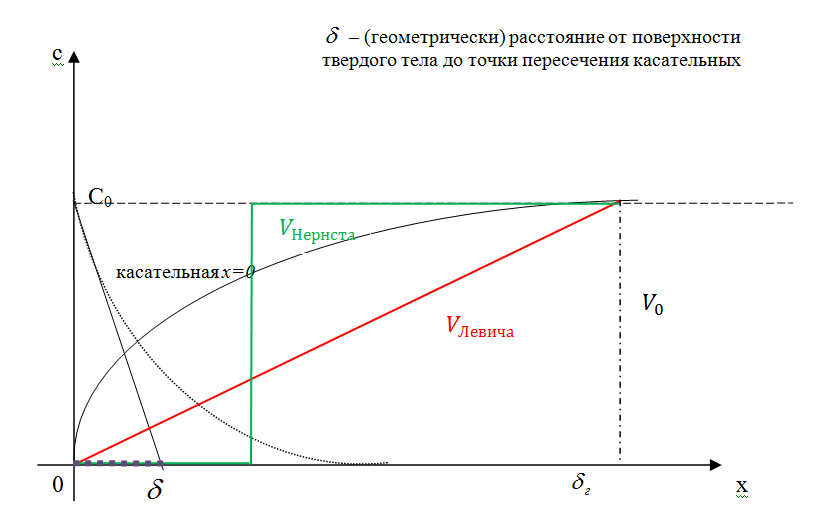
Задача Левича.
Рассмотрим набегание потока жидкости на пластину из труднорастворимой соли, которая растворяется с течением времени.
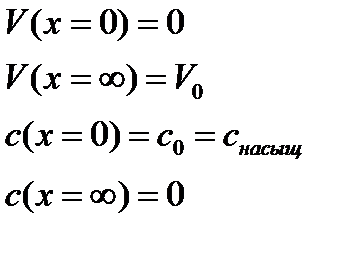
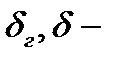
Для того чтобы описать поведение такой системы, необходимо решить совместно уравнение Навье-Стокса и уравнение конвективной диффузии. В данном случае, эти 2 системы уравнений не будут сцеплены между собой, так как имеется только вынужденная конвекция.
Если в системе можно пренебречь объемной силой F, тогда связь между уравнениями Навье-Стокса и конвективной диффузии теряется.
Для нахождения поля скоростей и поля концентрации сначала нужно решить систему уравнений Навье-Стокса и найти распределение скорости, а затем подставить найденное распределение скорости в уравнение конвективной диффузии и найти распределение поля концентрации. Эту задачу для данного случая решил Левич в 1950 году.
Уравнения, описывающие процесс изменения концентрации:
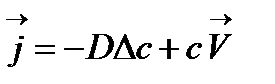 – уравнение конвективной диффузии, – уравнение конвективной диффузии, | (3.1) |
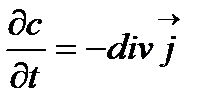 , – закон сохранения , – закон сохранения | (3.2) |
Граничные условия скорости:
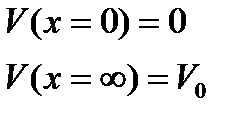 | (3.3) |
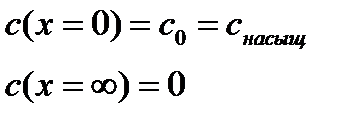 | (3.4) |
Уравнения (3.1), (3.2) можно объединить, подставив уравнение (3.1) в уравнение (3.2). Получим:
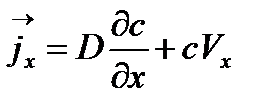 | (3.5) |
(Если скорость жидкости ламинарная, то нормальная составляющая скорости равна нулю, т е 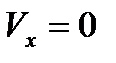
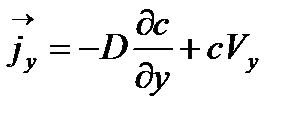 | (3.6) |
Режим стационарный, т е:
Учитывая, что некоторые слагаемые обращаются в ноль, получим:
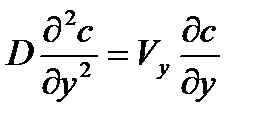 | (3.7) |
Распределение скоростей находятся из уравнений Навье-Стокса
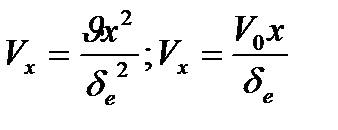 | (3.8) |
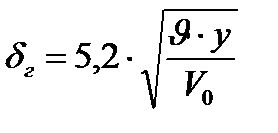 — гидродинамический погранслой (слой, где чувствуется «прилипание») — гидродинамический погранслой (слой, где чувствуется «прилипание») | (3.9) |
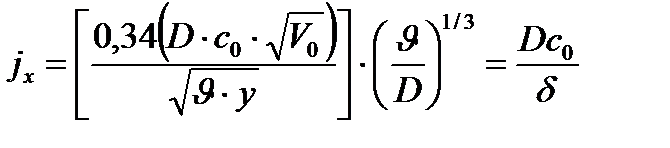 , , | (3.10) |
Тогда 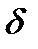
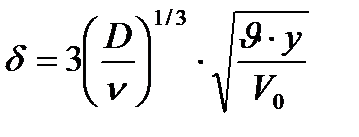 — толщина диффузионного погранслоя — толщина диффузионного погранслоя | (3.11) |
Сравним (3.9) и (3.11), получим
Отсюда, приведя к одной размерности, получим:
Таким образом, толщина диффузионного концентрационного погранслоя ≈ в 10 раз меньше, чем толщина гидродинамического погранслоя.
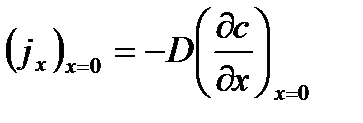 , при x=0, , при x=0,  =0 =0 | (3.12) |
Полагаем, что все изменение концентрации происходит внутри пограничного слоя.
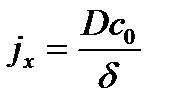 , , | (3.13) |
(3.13) было получено путем интегрирования уравнения конвективной диффузии при достаточно грубых упрощениях, а именно, мы предположили, что вблизи поверхности твердого тела имеется тонкий слой, внутри которого 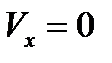
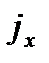
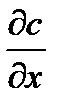
Если сравнить (3.12) и (3.13), то получим:
От (3.12) можно перейти к закону Фика:
В уравнении Нернста