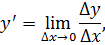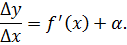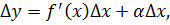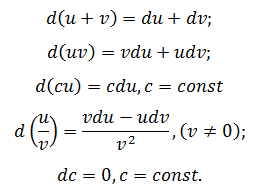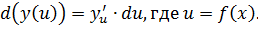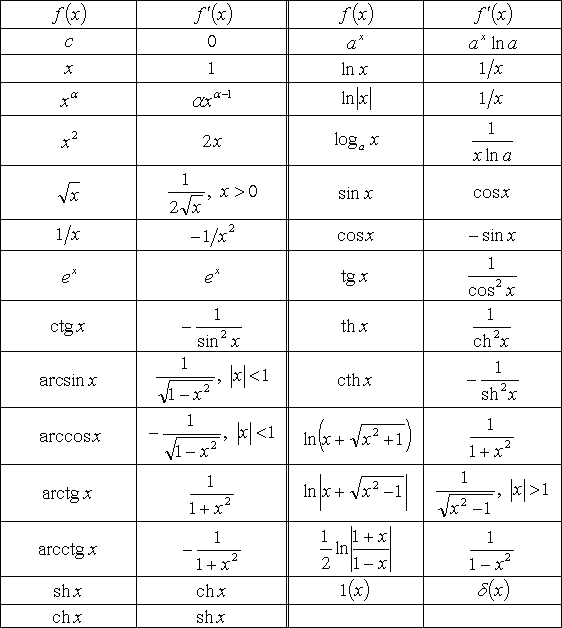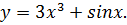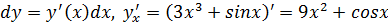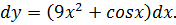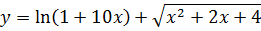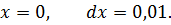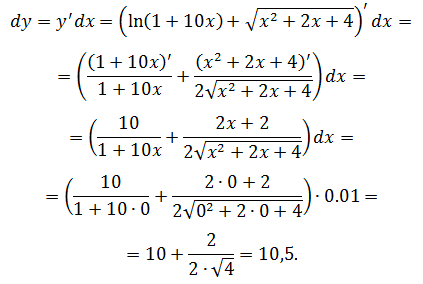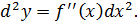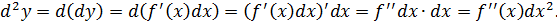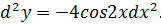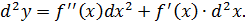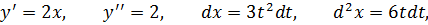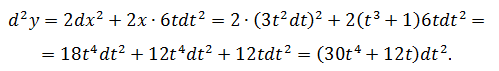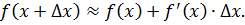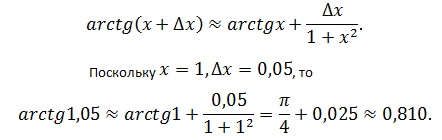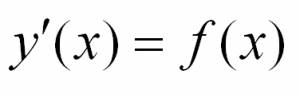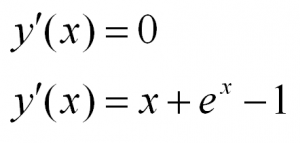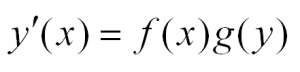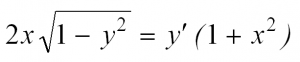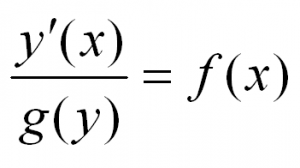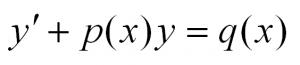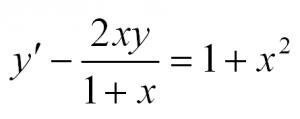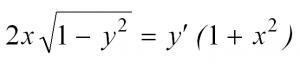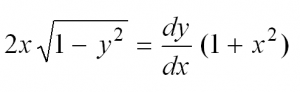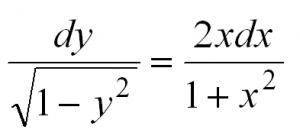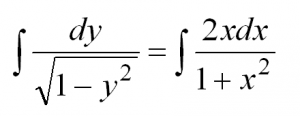Что такое дифференциация в математике
При выполнении некоторых расчётов в исследованиях, проектировании, анализе полученных опытных путём данных часто возникает необходимость предварительной прикидки результата, которую удобно выполнять, используя дифференциал функции. Приближённые вычисления, выполненные с его помощью, могут дать новые направления дальнейшего изучения объектов и их разработок.
Понятие и геометрический смысл дифференциала
Пусть y = f (x) имеет производную
Применяя свойства предела функции, получают равенство
После умножения обеих частей на приращение аргумента Δx, образуется тождество:
в котором в правой части записано слагаемое, являющееся бесконечно малой одного порядка с Δx, далее идет слагаемое более высокого порядка.
Определение 1
Дифференциалом функции y = f (x) первого порядка называется главная часть её приращения f′(x)Δx, которую обозначают dy (или d(f(x)).
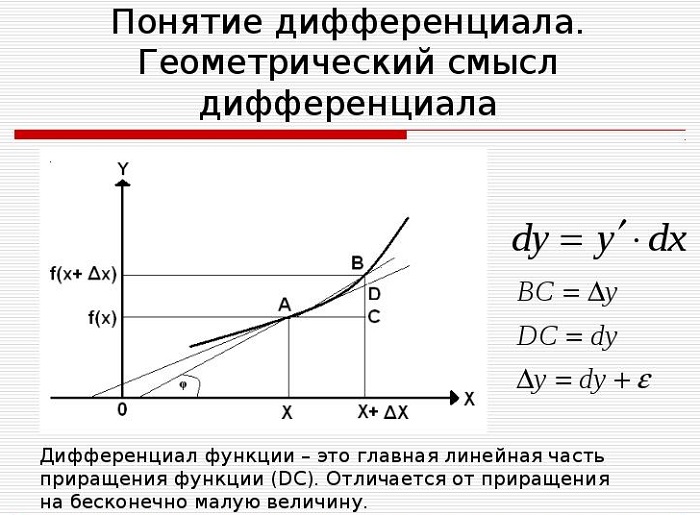
Для наглядного представления и понимания определения рассматривается касательная к графику функции y = f(x) в точке x. Когда значение переменной сдвигается по построенной прямой (получает приращение) на некоторую малую величину Δx, значение второй координаты точки тоже меняется.
Значит, дифференциал функции y = f(x) в точке x равен приращению ординаты касательной, когда её абсцисса меняется на величину Δx.
Определение 2
Дифференциал от дифференциала называется дифференциалом второго порядка. Таким же рекуррентным образом вводятся понятия дифференциалов более высоких порядков.
Формы записи дифференциала
Для нахождения дифференциала независимой переменной рассматривают функцию y = x, учитывая, что x’ = 1, а, следовательно:
Отсюда получается формула:
Для второго порядка вводится обозначение d 2 y.
Свойства дифференциала
Существующая таблица производных помогает выделить некоторые свойства дифференциалов, например, для суммы, произведения, частного получаются следующие правила:
Одним из важных свойств является инвариантность (неизменность) формы записи, независимо от того, является ли функция элементарной или композицией элементарных (сложной). Фактически,
Примеры решения задач
Задача №1
Найти дифференциал функции
Задача №2
Вычислить значение дифференциала функции
В помощь студентам создан онлайн калькулятор, который позволяет ввести функцию, нажать кнопку и получить форму или значение дифференциала.
Если dx есть константа, то для высших порядков имеет место следующая формула:
Этот результат вытекает непосредственно из определения:
Задача №3
Найти d 2 y, если y = cos2x и x – независимая переменная.
Если x – функция от некоторой другой независимой переменной, то свойство инвариантности перестаёт работать, следовательно,
Задача №4
Найти d 2 y, если y = x 2 и x = t 3 + 1, t – независимый аргумент.
Нетрудно заметить, что если выразить y напрямую через t, то получится тот же результат.
с высокой степенью точности можно вычислить приращение любой дифференцируемой зависимости.
Раскрыв Δy, сделав соответствующие преобразования, приходят к формуле приближённых вычислений:
Задача №5
Вычислить приближённо arctg1,05.
Пусть f(x) = arctg x. Тогда
Полный дифференциал функции
Математика не ограничивается множеством функций одного независимого аргумента. Рассматриваются зависимости от двух и более переменных.
Определения похожи, отличается вид главной части. Рассматриваются несколько слагаемых.
Например, если z = f(x;y) то
Последнее равенство есть формула полного дифференциала. Для функции нескольких переменных сохраняется принцип построения.
Если рассматривают приращения только по одной переменной, то приходят к понятию частных дифференциалов.
Заключение
Высшая математика позволяет находить приближённо общий корень системы уравнений, пользуясь дифференциальным исчислением, делать прикидку результатов, прогнозировать получаемое.
Производная как смысл жизни или что такое дифференциал(d)
Пролог:
Эта одна из статей серии «Производная как смысл жизни», сначала я хотел сделать одну огромную статью про почти все темы по дифференцированию, но я передумал и сделаю несколько статей, возможно так даже будет легче для людей которые пытаются найти конкретную для себя тему.
Начало
Для начала лучше ознакомиться со статьей о самой прозводной (скоро будет). Ну если вы ознакомились, или уже были ознакомлены то идем дальше.
Как мы уже знаем формула записи производной выглядит так:
Мы должны понимать, что если мы уберем предел, то к f'(x) прибавиться коофициент, я ее называю «неточность».
Так же вполне логично, что при Δx->0, β->0, так как чем меньше мы делаем разницу между x и x₀, тем меньше значение «неточности»(в статье о производной об этом подробнее рассказано).
Теперь выразим из этого равенства приращение функции(Δy):
И на этом следует пока остановиться и рассмотреть график.
Смотрим дифференциалу в лицо
Расмотрим такой график:
Как мы знаем производная в точке равняется значению тангенса угла в этой точке, то есть f'(x)=tg(α). Так что давайте обозначим производную, ну и приращения которыми она ограничена.
Зная это введем обозначение на графике:
Вернемся к равенству
BD = Δy и мы знаем, что BD = BC + CD, а значит Δy = BC + CD, где BC мы назвали главной линейной частью приращения функции(dy), следовательно Δy = dy + βΔx.
Из формулы мы понимаем, что dy=f'(x)Δx.
Хорошо, мы определили чему равен дифференциал функции, а что же тогда является дифференциалом независимой пременной функции(аргумента).
Графически мы видим, что Δx никак не разделена касательной, то есть Δx это полное приращение функции, а значит dx = Δx.
Так же мы можем найти по формуле: dx = (x)’Δx = 1*Δx = Δx
И зная, что dy = f'(x)dx, мы можем выразить производную: f'(x)=dy/dx.
Немного пределов
Добавим с левой части и с правой предел
В самом начале мы сказали, что если β->0, то Δx->0 и наборот, а значит:
Зная, что f'(x)Δx = dy, мы делаем вывод, что:
Дифференциальные уравнения для «чайников». Примеры решения
Часто одно лишь упоминание дифференциальных уравнений вызывает у студентов неприятное чувство. Почему так происходит? Чаще всего потому, что при изучении основ материала возникает пробел в знаниях, из-за которого дальнейшее изучение диффуров становиться просто пыткой. Ничего не понятно, что делать, как решать, с чего начать?
Однако мы постараемся вам показать, что диффуры – это не так сложно, как кажется.
Основные понятия теории дифференциальных уравнений
Со школы нам известны простейшие уравнения, в которых нужно найти неизвестную x. По сути дифференциальные уравнения лишь чуточку отличаются от них – вместо переменной х в них нужно найти функцию y(х), которая обратит уравнение в тождество.
Дифференциальные уравнения имеют огромное прикладное значение. Это не абстрактная математика, которая не имеет отношения к окружающему нас миру. С помощью дифференциальных уравнений описываются многие реальные природные процессы. Например, колебания струны, движение гармонического осциллятора, посредством дифференциальных уравнений в задачах механики находят скорость и ускорение тела. Также ДУ находят широкое применение в биологии, химии, экономике и многих других науках.
Дифференциальное уравнение (ДУ) – это уравнение, содержащее производные функции y(х), саму функцию, независимые переменные и иные параметры в различных комбинациях.
Существует множество видов дифференциальных уравнений: обыкновенные дифференциальные уравнения, линейные и нелинейные, однородные и неоднородные, дифференциальные уравнения первого и высших порядков, дифуры в частных производных и так далее.
Решением дифференциального уравнения является функция, которая обращает его в тождество. Существуют общие и частные решения ДУ.
Общим решением ДУ является общее множество решений, обращающих уравнение в тождество. Частным решением дифференциального уравнения называется решение, удовлетворяющее дополнительным условиям, заданным изначально.
Порядок дифференциального уравнения определяется наивысшим порядком производных, входящих в него.
Обыкновенные дифференциальные уравнения
Обыкновенные дифференциальные уравнения – это уравнения, содержащие одну независимую переменную.
Рассмотрим простейшее обыкновенное дифференциальное уравнение первого порядка. Оно имеет вид:
Решить такое уравнение можно, просто проинтегрировав его правую часть.
Примеры таких уравнений:
Уравнения с разделяющимися переменными
В общем виде этот тип уравнений выглядит так:
Решая такое уравнение, нужно разделить переменные, приведя его к виду:
После этого останется проинтегрировать обе части и получить решение.
Линейные дифференциальные уравнения первого порядка
Такие уравнения имеют вид:
Здесь p(x) и q(x) – некоторые функции независимой переменной, а y=y(x) – искомая функция. Приведем пример такого уравнения:
Решая такое уравнение, чаще всего используют метод вариации произвольной постоянной либо представляют искомую функцию в виде произведения двух других функций y(x)=u(x)v(x).
Для решения таких уравнений необходима определенная подготовка и взять их “с наскока” будет довольно сложно.
Пример решения ДУ с разделяющимися переменными
Вот мы и рассмотрели простейшие типы ДУ. Теперь разберем решение одного из них. Пусть это будет уравнение с разделяющимися переменными.
Сначала перепишем производную в более привычном виде:
Затем разделим переменные, то есть в одной части уравнения соберем все «игреки», а в другой – «иксы»:
Теперь осталось проинтегрировать обе части:
Интегрируем и получаем общее решение данного уравнения:
Конечно, решение дифференциальных уравнений – своего рода искусство. Нужно уметь понимать, к какому типу относится уравнение, а также научиться видеть, какие преобразования нужно с ним совершить, чтобы привести к тому или иному виду, не говоря уже просто об умении дифференцировать и интегрировать. И чтобы преуспеть в решении ДУ, нужна практика (как и во всем). А если у Вас в данный момент нет времени разбираться с тем, как решаются дифференциальные уравнения или задача Коши встала как кость в горле или вы не знаете, как правильно оформить презентацию, обратитесь к нашим авторам. В сжатые сроки мы предоставим Вам готовое и подробное решение, разобраться в подробностях которого Вы сможете в любое удобное для Вас время. А пока предлагаем посмотреть видео на тему «Как решать дифференциальные уравнения»:
Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.
Дифференциал и производная разница
Чтобы лучше понять разницу между дифференциалом и производной функции, вам нужно сначала понять концепцию функции.
Функция является одной из основных концепций математики, которая определяет взаимосвязь между набором входов и множеством возможных выходов, где каждый вход связан с одним выходом. Одной переменной является независимая переменная, а другая переменная – зависимая переменная.
Концепция функции является одной из самых недооцененных тем в математике, но имеет важное значение для определения физических отношений. Возьмем, к примеру: утверждение «y является функцией x» означает, что что-то, связанное с y, напрямую связано с x по какой-либо формуле. Скажем, если входной сигнал равен 6, а функция – добавить 5 к входу 6. Результат будет 6 + 5 = 11, что является вашим выходом.
В математике есть несколько исключений, или вы можете сказать о проблемах, которые не могут быть решены обычными методами геометрии и алгебры. Для решения этих проблем используется новая ветвь математики, известная как исчисление.
Исчисление принципиально отличается от математики, которая не только использует идеи из геометрии, арифметики и алгебры, но также имеет дело с изменением и движением.
Исчисление как инструмент определяет производную функции как предел определенного вида. Понятие производной функции отличает исчисление от других отраслей математики. Дифференциал – это подполе исчисления, которое относится к бесконечно малой разности в некоторой переменной величине и является одним из двух фундаментальных делений исчисления. Другая ветвь называется интегральным исчислением.
Что такое Дифференциал?
Дифференциал – одно из фундаментальных делений исчисления, а также интегральное исчисление. Это подполе исчисления, которое имеет дело с бесконечно малым изменением в некоторой переменной величине. Мир, в котором мы живем, наполнен взаимосвязанными количествами, которые меняются периодически.
Дифференциальные уравнения – это уравнения, содержащие неизвестные функции и некоторые их производные.
Что такое производная?
Понятие производной функции является одним из самых мощных понятий в математике. Производной функции обычно является новая функция, которая называется производной функцией или функцией скорости.
Производная функции представляет собой мгновенную скорость изменения значения зависимой переменной по отношению к изменению значения независимой переменной. Это фундаментальный инструмент исчисления, который также можно интерпретировать как наклон касательной линии. Он измеряет, насколько крутой график функции находится в некоторой заданной точке графика.
Проще говоря, производная – это скорость, с которой функция изменяется в какой-то определенной точке.
Разница между дифференциальными и производными
Определение дифференциального Vs. производный
Оба термина дифференциальные и производные тесно связаны друг с другом с точки зрения взаимосвязи. В математике меняющиеся сущности называются переменными, а скорость изменения одной переменной по отношению к другой называется производной.
Уравнения, определяющие связь между этими переменными и их производными, называются дифференциальными уравнениями. Дифференциация – это процесс нахождения производной. Производной функции является скорость изменения выходного значения по отношению к его входному значению, тогда как дифференциал – это фактическое изменение функции.
Связь дифференциальных Vs. производный
Дифференциация – это метод вычисления производной, которая является скоростью изменения выхода y функции относительно изменения переменной x.
Проще говоря, производная относится к скорости изменения y по х, и это соотношение выражается как y = f (x), что означает, что y является функцией x. Производные функции f (x) определяются как функция, значение которой порождает наклон f (x), где она определена, и f (x) дифференцируема. Это относится к наклону графика в данной точке.
Представление дифференциального Vs. производный
Дифференциалы представлены как dИкс, dу, dt и т. д., где dx представляет собой небольшое изменение x, dy представляет собой небольшое изменение y и dt – небольшое изменение t. При сравнении изменений связанных величин, где y – функция x, дифференциал dy может быть записана как:
Производной функции является наклон функции в любой точке и записывается как d/dИкс. Например, производную от sin (x) можно записать в виде:
d/dx sin (x) = sin (x) ’ = cos (x)
Дифференциальная и производная: Сравнительная таблица
Резюме дифференциальных Vs. производный
В математике скорость изменения одной переменной по отношению к другой переменной называется производной, а уравнения, выражающие связь между этими переменными и их производными, называются дифференциальными уравнениями.В двух словах, дифференциальные уравнения включают производные, которые фактически определяют, как изменяется количество относительно другого. Решая дифференциальное уравнение, вы получаете формулу для количества, не содержащего производных. Метод вычисления производной называется дифференцированием. Проще говоря, производной функции является скорость изменения выходного значения по отношению к его входному значению, тогда как дифференциал – это фактическое изменение функции.
Центральные понятия дифференциального исчисления — производная и дифференциал возникли при рассмотрении множества задач естествознания и математики, каждая из которых приводила к вычислению пределов одного типа.
Производная функции
имеет конечный предел при стремлении приращения независимой переменной к 0, то такой предел называется производной функции f(х) при заданном х.
Производная функции – одно из основных понятий математики, а в математическом анализе производная наряду с интегралом занимает центральное место.
Дифференцирование
Процесс нахождения производной называется дифференцированием. Обратная операция – восстановление функции по известной производной –интегрированием.
Для нахождения производной функции f(x) в точке x0 на основе определения следует выполнить следующие действия:
Производная сложной функции равна произведению производной по промежуточной переменной по независимой переменной:
Попробуй обратиться за помощью к преподавателям
Найти производную функции
Вычислить производную функции
По формуле разности функций вычислим производную
За f(x) примем числитель, а за g(x) – знаменатель
Найдем производные отдельные множителей и упростим дробь
Задай вопрос специалистам и получи
ответ уже через 15 минут!
Найти производную сложной функции
По правилу нахождения производной сложной функции вычислим производную и умножим ее на производную подкоренного выражения.
Дифференциал
Дифференциалом функции называется произведение производной этой функции на приращение независимой переменной.
Дифференциал функции обозначается dy и имеет запись вида:
Найти дифференциал функции.
По правилу дифференцирования, дифференциал суммы равен сумме дифференциалов функций.
Найдем производные данных функций и добавим к ним знак дифференциала. Производная второй функции так же как и дифференциал равна 0.
Найти дифференциал функции.
По правилу дифференцирования:
Найдем производные данных функций и добавим к ним знак дифференциала.
[d(e^ cos x)=e^ dxcdot cos x-e^ sin xdx]
Так и не нашли ответ
на свой вопрос?
Просто напиши с чем тебе
нужна помощь