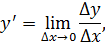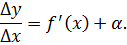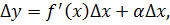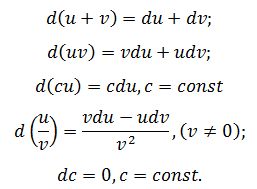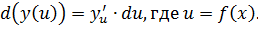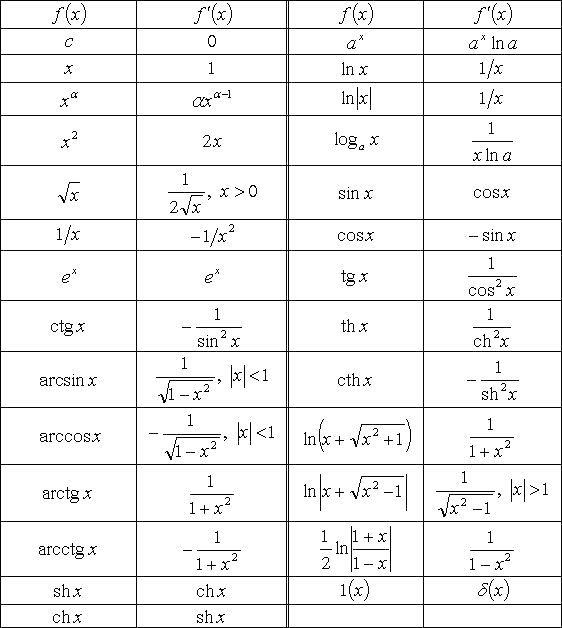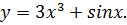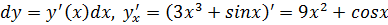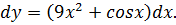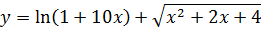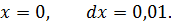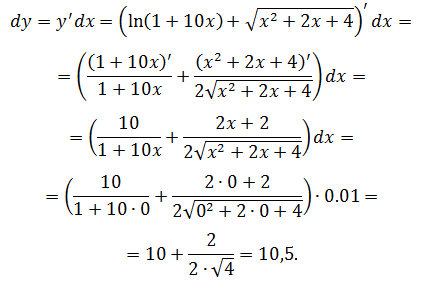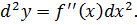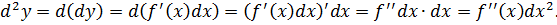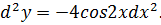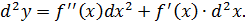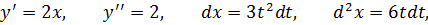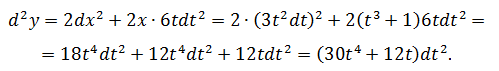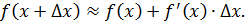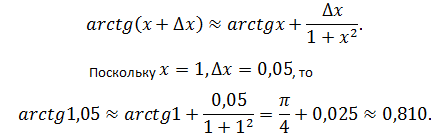Что такое дифференциальное исчисление в математике

Дифференциальное и интегральное исчисление

Математи́ческий ана́лиз — совокупность разделов математики, посвященных исследованию функций и их обобщений методами дифференциального и интегрального исчислений. При столь общей трактовке к анализу следует отнести и функциональный анализ вместе с теорией интеграла Лебега, комплексный анализ (ТФКП), изучающий функции, заданные на комплексной плоскости, нестандартный анализ, изучающий бесконечно малые и бесконечно большие числа, а также вариационное исчисление.

В учебном процессе к анализу относят

При этом элементы функционального анализа и теории интеграла Лебега даются факультативно, а ТФКП, вариационное исчисление, теория дифференциальных уравнений читаются отдельными курсами. Строгость изложения следует образцам конца XIX века и в частности использует наивную теорию множеств.

Содержание

Исторический очерк

Предшественниками математического анализа были античный метод исчерпывания и метод неделимых. Все три направления, включая анализ, роднит общая исходная идея: разложение на бесконечно малые элементы, природа которых, впрочем, представлялась авторам идеи довольно туманно. Алгебраический подход (исчисление бесконечно малых) начинает появляться у Валлиса, Джеймса Грегори и Барроу. В полной мере новое исчисление как систему создал Ньютон, который, однако, долгое время не публиковал свои открытия. [2]

Лейбниц и его ученики

Эти определения поясняются геометрически, при этом на рис. бесконечно малые приращения изображены конечными. Рассмотрение опирается на два требования (аксиомы). Первое:

Требуется, чтобы две величины, отличающиеся друг от друга лишь на бесконечно малую величину, можно было брать [при упрощении выражений?] безразлично одну вместо другой. [7]

и проч. правила дифференцирования. Второе требование гласит:

Требуется, чтобы можно было рассматривать кривую линию как совокупность бесконечного множества бесконечно малых прямых линий. [8]

,

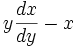
достигающее экстремальных значений в точках перегиба кривой, отношению же dy к dx не придается никакого особого значения.

Но всякая непрерывно возрастающая или убывающая величина не может превратиться из положительной в отрицательную, не проходя через бесконечность или нуль… Отсюда следует, что дифференциал наибольшей и наименьшей величины должен равняться нулю или бесконечности. [10]

Эйлер

Функция переменного количества есть аналитическое выражение, составленное каким-либо образом из этой переменного количества и чисел или постоянных количеств. [16]

Подчеркивая, что «основное различие функций лежит в способе составления их из переменного и постоянных», Эйлер перечисляет действия, «посредством которых количества могут друг с другом сочетаться и перемешиваться; действиями этими являются: сложение и вычитание, умножение и деление, возведение в степень и извлечение корней; сюда же следует отнести также решение [алгебраических] уравнений. Кроме этих действий, называемых алгебраическими, существует много других, трансцендентных, как-то: показательные, логарифмические и бесчисленные другие, доставляемые интегральным исчислением». [17] Такая трактовка позволяла без труда обращаться с многозначными функциями и не требовала пояснения, над каким полем рассматривается функция: выражение для счета определено для комплексных значений переменных даже тогда, когда для рассматриваемой задачи это не нужно.

,

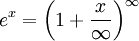
в котором лишь поздние авторы видели предельный переход. С аналитическими выражениями производились разнообразные преобразования, позволившие Эйлеру найти представления для элементарных функций в виде рядов, бесконечных произведений и т. д. Эйлер преобразует выражения для счета так, как это делают в алгебре, не обращая внимания на возможность вычислить значение функции в точке по каждой из написанных формул.

Сам ход доказательства прекрасно демонстрирует технику использования бесконечно большого. Определив синус и косинус при помощи тригонометрического круга, Эйлер выводит из формул сложения следующее:

,

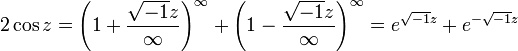
отбрасывая бесконечно малые величины большего порядка. Используя это и аналогичное выражение, Эйлер получает и свою знаменитую формулу

.

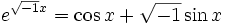
Указав различные выражения для функций, которые теперь называют элементарными, Эйлер переходит к рассмотрению кривых на плоскости, начертанным свободным движением руки. По его мнению, не для всякой такой кривой можно отыскать единое аналитическое выражение (см. также Спор о струне). [20] В XIX веке с подачи Казорати [21] это утверждение считалось ошибочным: по теореме Вейерштрасса всякая непрерывная в современном смысле кривая может быть приближенно описана полиномами. На самом деле Эйлера это едва ли убедило, ведь нужно еще переписать предельный переход при помощи символа .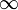

В трехтомном интегральном исчислении Эйлер трактует вводит понятие интеграла так:

Лагранж

Следующим крупным произведением, сыгравшим значительную роль в развитии концепции анализа, явилась Теория аналитических функций [23] Лагранжа и обширный пересказ работ Лагранжа, выполненный Лакруа [24] в несколько эклектической манере.

,

,

и т. д. [25]

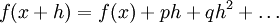
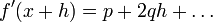
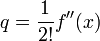
Такой подход к трактовке понятия производной используется в современной алгебре и послужил основой для создания теории аналитических функций Вейерштрасса.

Лагранж оперировал такими рядами как формальными и получил ряд замечательных теорем. В частности, впервые и вполне строго доказал разрешимость начальной задачи для обыкновенных дифференциальных уравнений в формальных степенных рядах. [26]

Вопрос об оценке точности приближений, доставляемых частными суммами ряда Тейлора, впервые был поставлен именно Лагранжем: в конце Теории аналитических функций он вывел то, что теперь называют формулой Тейлора с остаточным членом в форме Лагранжа. [27] Однако, в противоположность современным авторам, Лагранж не видел нужды в употреблении этого результата для обоснования сходимости ряда Тейлора.

Вопрос о том, действительно ли функции, употребимые в анализе, могут быть разложены в степенной ряд, в последствие стал предметом дискуссии. Конечно, Лагранжу было известно, что в некоторых точках элементарные функции могут не разлагаться в степенной ряд, однако в этих точка они и недифференцируемы ни в каком смысле. Коши в своём Алгебраическом анализе привел в качестве контрпримера функцию

.

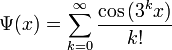
Дальнейшее развитие

В XIX веке Коши первым дал анализу твердое логическое обоснование, введя понятие последовательности, он же открыл новую страницу комплексного анализа. Пуассон, Лиувилль, Фурье и другие изучали дифференциальные уравнения в частных производных и гармонический анализ.

В последней трети XIX века Вейерштрасс произвёл арифметизацию анализа, полагая геометрическое обоснование неудобным, и предложил определение предела через ε-δ-язык;. Тогда математики стали сомневаться в существовании множества вещественных чисел. Дедекинд ввёл вещественные числа с помощью дедекиндовых сечений. В это время попытки усовершенствования теоремы об интегрируемости по Риману привели к созданию классификации разрывности вещественных функций. Также были открыты «патологические» примеры (нигде не дифференцируемые непрерывные функции, заполняющие пространство кривые). В связи с этим Жордан разработал теорию меры, а Кантор — теорию множеств, и в начале XX века математический анализ был формализован с их помощью.

Источник

При выполнении некоторых расчётов в исследованиях, проектировании, анализе полученных опытных путём данных часто возникает необходимость предварительной прикидки результата, которую удобно выполнять, используя дифференциал функции. Приближённые вычисления, выполненные с его помощью, могут дать новые направления дальнейшего изучения объектов и их разработок.

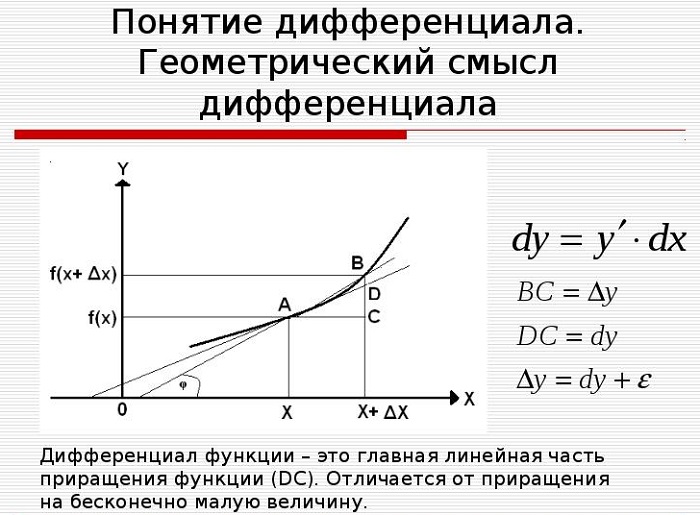
Понятие и геометрический смысл дифференциала

Пусть y = f (x) имеет производную

Применяя свойства предела функции, получают равенство

После умножения обеих частей на приращение аргумента Δx, образуется тождество:

в котором в правой части записано слагаемое, являющееся бесконечно малой одного порядка с Δx, далее идет слагаемое более высокого порядка.

Определение 1

Дифференциалом функции y = f (x) первого порядка называется главная часть её приращения f′(x)Δx, которую обозначают dy (или d(f(x)).

Для наглядного представления и понимания определения рассматривается касательная к графику функции y = f(x) в точке x. Когда значение переменной сдвигается по построенной прямой (получает приращение) на некоторую малую величину Δx, значение второй координаты точки тоже меняется.

Значит, дифференциал функции y = f(x) в точке x равен приращению ординаты касательной, когда её абсцисса меняется на величину Δx.

Определение 2

Дифференциал от дифференциала называется дифференциалом второго порядка. Таким же рекуррентным образом вводятся понятия дифференциалов более высоких порядков.

Формы записи дифференциала

Для нахождения дифференциала независимой переменной рассматривают функцию y = x, учитывая, что x’ = 1, а, следовательно:

Отсюда получается формула:

Для второго порядка вводится обозначение d 2 y.

Свойства дифференциала

Существующая таблица производных помогает выделить некоторые свойства дифференциалов, например, для суммы, произведения, частного получаются следующие правила:

Одним из важных свойств является инвариантность (неизменность) формы записи, независимо от того, является ли функция элементарной или композицией элементарных (сложной). Фактически,

Примеры решения задач

Задача №1

Найти дифференциал функции

Задача №2

Вычислить значение дифференциала функции

В помощь студентам создан онлайн калькулятор, который позволяет ввести функцию, нажать кнопку и получить форму или значение дифференциала.

Если dx есть константа, то для высших порядков имеет место следующая формула:

Этот результат вытекает непосредственно из определения:

Задача №3

Найти d 2 y, если y = cos2x и x – независимая переменная.

Если x – функция от некоторой другой независимой переменной, то свойство инвариантности перестаёт работать, следовательно,

Задача №4

Найти d 2 y, если y = x 2 и x = t 3 + 1, t – независимый аргумент.

Нетрудно заметить, что если выразить y напрямую через t, то получится тот же результат.

с высокой степенью точности можно вычислить приращение любой дифференцируемой зависимости.

Раскрыв Δy, сделав соответствующие преобразования, приходят к формуле приближённых вычислений:

Задача №5

Вычислить приближённо arctg1,05.

Пусть f(x) = arctg x. Тогда

Полный дифференциал функции

Математика не ограничивается множеством функций одного независимого аргумента. Рассматриваются зависимости от двух и более переменных.

Определения похожи, отличается вид главной части. Рассматриваются несколько слагаемых.

Например, если z = f(x;y) то

Последнее равенство есть формула полного дифференциала. Для функции нескольких переменных сохраняется принцип построения.

Если рассматривают приращения только по одной переменной, то приходят к понятию частных дифференциалов.

Заключение

Высшая математика позволяет находить приближённо общий корень системы уравнений, пользуясь дифференциальным исчислением, делать прикидку результатов, прогнозировать получаемое.

Источник

История применения дифференцированного исчисления

Дифференциальное исчисление было создано Ньютоном и Лейбницем в конце 17 столетия на основе двух задач:

1)о разыскании касательной к произвольной линии

2)о разыскании скорости при произвольном законе движения

Еще раньше понятие производной встречалось в работах итальянского математика Тартальи (около 1500-1557 гг.) – здесь появилась касательная в ходе изучения вопроса об угле наклона орудия, при котором обеспечивается наибольшая дальность полета снаряда.

Производная в математике показывает числовое выражение степени изменений величины, находящейся в одной и тоже точке, под влиянием различных условий.

Формула производной часто встречается в работах известных математиков 17 века. Её применяли Ньютон и Лейбниц. Ей посвятил целый трактат в математике известный учёный Галилео Галилей. Затем производная и различные изложения с её применением стали встречаться в работах Декарта, французского математика Роберваля и англичанина Грегори. Большой вклад по изучению производной внесли такие умы, как Лопиталь, Бернулли, Лагранж.

Дифференциальное исчисление – широко применяемый для экономического анализа математический аппарат. Базовой задачей экономического анализа является изучение связей экономических величин, записанных в виде функций. В каком направлении изменится доход государства при увеличении налогов или при введении импортных пошлин. Увеличится или уменьшится выручка фирмы при повышении цены на ее продукцию. В какой пропорции дополнительное оборудование может заменить выбывающих работников. Для решения подобных задач должны быть построены функции связи входящих в них переменных, которые затем изучаются с помощью методов дифференциального исчисления. В экономике очень часто требуется найти наилучшее или оптимальное значение показателя: наивысшую производительность труда, максимальную прибыль, максимальный выпуск, минимальные издержки и т.д. Каждый показатель представляет собой функцию от одного или нескольких аргументов. Таким образом, нахождение оптимального значения показателя сводиться к нахождению экстремума функции.

Применение производной позволяет увидеть планируемые действия, понять их необходимость, тем самым, помогая экономистам в составлении успешных бизнес-планов.

Производная – основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если таковой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке). Процесс вычисления производной называется дифференцированием. Обратный процесс – интегрирование.

Определение производной, выдерживая определённую концепцию, по – своему преподносят в современных учебниках Алимов, Башмаков и Колмагоров.

Принято считать, что трактовка производной Алимовым в учебнике направлена в основном на то, каким образом применяются формулы производной на практике. Каждое дополнение к понятию производной автор обязательно закрепил задачами.

Колмогоров отводит данной теме более большой объём. Может быть, характер производной раскрыт более сложно и вызывает затруднения, но подробная детализация некоторых аспектов гарантирует высокую подготовку.

Учебник Башмакова принято считать более подходящим для самостоятельного изучения материала. Понятия производной Башмаков излагает очень кратко, но последовательность доказательств помогает просто и понятно вникнуть в тему. Особая характерная черта – Башмаков все абстрактные математические понятия «воплощает» в жизни, предлагая конкретные примеры.

Заключение: Применение производной довольно широко. Однако в наше время, в связь с научно-техническим прогрессом, в частности с быстрой эволюцией вычислительных систем, дифференциальное исчисление становиться всё более актуальными в решении как простых, так и сверхсложных задач.

Лейбниц и дифференциальное исчисление

Введение

Исследованиями в области дифференциальных исчислений занимались многие знаменитые ученые, Ньютон, Лейбниц, Барроу и др. Однако главная заслуга принадлежит Готфриду Вильгельму Лейбницу.

Ученый установил четкие правила для простейших операций, из которых строятся более сложные, и постоянную связь их с определенной системой обозначений. Метод Лейбница был представлен в такой форме, которую легко можно было усвоить и затем применять механически, придерживаясь определенных правил для простых операций. Это было преимуществом для математиков, которые менее глубоко чувствовали предмет. Данное обстоятельство привело к созданию школы Лейбница.

Родился Лейбниц в Лейпциге. В 1661 поступил на юридический факультет Лейпцигского университета. Кроме юридических наук изучал философию и математику, занимался вопросами химии, геологии, конструированием ветряного двигателя для насосов, выкачивающих воду из шахт. Особенно плодотворной была научная деятельность Лейбница в области математики.

На изучение Лейбницем математики большое влияние оказал Гюйгенс. Последний предложил задачу определения суммы чисел, обратных треугольным, т. е. чисел вида

.

Но на решении этой задачи Лейбниц не остановился, он нашел также сумму чисел, обратных пирамидальным, и других рядов, что явилось подготовкой к созданию дифференциального исчисления.

Лейбниц продолжил работу в этом направлении, штудируя труды Кавальери, Григория и Паскаля в области инфинитезимальных исследований. Ученый усвоил работы в этой области настолько, что мог применять их самостоятельно, что доказал новым инфинитезимальным преобразованием, из которого получалось большинство известных на тот период квадратур. Теперь это преобразование получают из выражения для площади сектора, ограниченного двумя радиусами-векторами и бесконечно малой дугой. Сам Лейбниц при создании дифференциального исчисления, также пользовался этим дифференциальным выражением. В более же ранних своих рукописях и письмах он использует ту же геометрическую форму, что давали и его предшественники.

На рис. 1 к кривой AC проведена касательная EC, отсекающая отрезок AE. Этот отрезок берется в качестве ординаты BF точки F, которая обладает одинаковой абсциссой с точкой C. Площадь, ограниченная геометрическим местом этой точки, осью абсцисс и двумя ординатами, больше площади сектора, ограниченного дугою кривой AC и радиусами-векторами, проведенными из A к ее концам, в два раза. Если рассмотреть бесконечно малые части этих фигур (прямоугольники и треугольники) то, из подобия треугольников можно увидеть, что основание и высота бесконечно малого прямоугольника обратно пропорциональны высоте и основанию соответствующего бесконечно малого треугольника.

Прямоугольные треугольники AHE и CDG подобны, следовательно, . Что в силу равенств и можно записать как:

.

Последнее равенство показывает, что площадь прямоугольника равна удвоенной площади сектора: .

Используя метод Ферма для определения касательных к параболам и гиперболам разных порядков, Лейбниц определил, что вспомогательная кривая также является параболой и гиперболой того же порядка, но с новым параметром. Таким образом, вычисляя площадь круга, ученый получил и разложил ее в ряд. Он нашел аналогичный ряд для .

Изучение бесконечных знакопеременных рядов привело ученого к рассмотрению сходимости таких рядов. Лейбниц выдвинул предположение, что бесконечный ряд с чередующимися знаками имеет конечную сумму при условии, что абсолютная величина членов убывает и стремится в пределе к нулю.

Независимо от изучения рядов Лейбниц выдвинул ряд мыслей по нахождению касательной к произвольной кривой при помощи характеристического треугольника, образованного разностями между абсциссами и между ординатами двух бесконечно близких точек и лежащей между этими точками дугою. Эти величины позже будут названы ученым dх,dу,dz. Но похожие размышления были обнаружены Лейбницем у Барроу и Грегори после изучения их работ. Однако исследователем были сделаны интересные наблюдения. Вследствие того, что при рассматриваемом определении касательных применяются разности dу между ординатами, которые соответствуют разностям между абсциссами dх, то в обратную сторону ордината уявляется суммой этих разностей. На основании того, что задача о квадратуре сводится к определению такой же суммы, Лейбниц высказывает мнение, что почти все учение об обратных задачах на касательные можно представить в виде квадратур. Таким образом, была установлена связь между дифференцированием и интегрированием.

В процессе работы над этими исследованиями ученый развил свою инфинитезимальную символику. Исследования также проводились по определенным установленным им правилам исчисления. Эти правила используются и теперь.

Заключение

Небольшое сочинение Лейбница, появившееся 1684 году, положило действительное начало исчислению бесконечно малых, дав правила, которые были достаточно просты для начала, и комбинация которых давала возможность дальнейшей работы. Оно открывает новую эпоху в истории математики. Сам Лейбниц уже ранее решал многие задачи исчисления бесконечно малых, чем то, что представлено в его работе.

Путем изучения литературы, через письменное и личное общение с другими математиками он усвоил существовавшие тогда методы и основательно их переработал. Благодаря этому он смог быстро двинуться вперед в своей работе.

Из всех современных ему математиков Лейбниц в наибольшей степени является лицом, с именем которого связано начало новой эпохи, в основном, благодаря тому, что наиболее значительные работы начала новой эпохи были созданы на основе введенных Лейбницем форм (это обстоятельство способствовало развитию последних), а также потому, что эти формы используются до сих пор.

Источник