Что такое диаграмма рассеяния
Диаграмма рассеяния
Из Википедии — свободной энциклопедии
Диаграмма рассеяния (также точечная диаграмма, англ. scatter plot ) — математическая диаграмма, изображающая значения двух переменных в виде точек на декартовой плоскости. Могут использоваться и полярные координаты, особенно в случаях, когда одна из переменных представляет собой физическое направление или имеет циклический характер.
На диаграмме рассеяния каждому наблюдению (или элементарной единице набора данных) соответствует точка, координаты которой равны значениям двух каких-то параметров этого наблюдения. Если предполагается, что один из параметров зависит от другого, то обычно значения независимого параметра откладывается по горизонтальной оси, а значения зависимого — по вертикальной. Диаграммы рассеяния используются для демонстрации наличия или отсутствия корреляции между двумя переменными.
В физике под диаграммой рассеяния обычно понимают подобную диаграмму для случая физического рассеяния частиц, при этом независимая переменная (представленная обычно горизонтальной декартовой координатой или углом в полярных координатах) представляет собой физический угол рассеяния частицы (в этом случае нередко используются полярные координаты) или энергию падающих частиц, а зависимая координата (вертикальная в декартовых или радиальная в полярных) — эффективное сечение рассеяния — может быть представлено, в том числе на одной диаграмме, и теоретическое значение (тогда нередко это непрерывная кривая), и экспериментальные оценки (часто в виде точек, дополненных изображением доверительных интервалов).
Диаграммы рассеивания



Часто приходится выяснять, существует ли зависимость между двумя различными параметрами процесса. Например, зависят ли изменения в диаметре отверстия от изменений скорости вращения сверла.
Обычно предполагается, что исследуемые параметры отражают характеристики качества и влияющие на них факторы. Чтобы понять, есть ли какая-либо связь между рассматриваемыми параметрами, используют диаграммы рассеивания.
Диаграмма рассеивания- это графическое представление пар исследуемых данных в виде множества точек на координатной плоскости.
Диаграмма рассеивания даёт возможность выдвинуть гипотезу о наличии или отсутствии корреляционной связи между двумя случайными величинами. При этом изучаются обычно величины, описывающие:
· характеристику качества и влияющий на неё фактор;
· две различные характеристики качества;
· два фактора, влияющие на одну характеристику качества.
Рисунок 4.17. Диаграмма рассеивания (положительная корреляция)
Диаграмма разброса 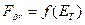

Эмпирическую линию регрессии строят обычно на этапе обработки опытных данных, но даже само расположение точек диаграммы рассеяния в факторном пространстве (у — х) без построения этой линии позволяет предварительно оценить вид и тесноту взаимосвязи у = f(x).
Взаимосвязь двух факторов может быть линейной или нелинейной, прямой или обратной, тесной или слабой (лёгкой) или вообще отсутствовать.
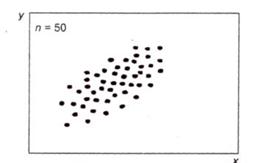
Рисунок 4.18а.Прямая корреляция
Рисунок 4.18б.Лёгкая прямая корреляция
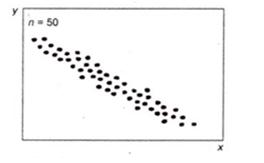
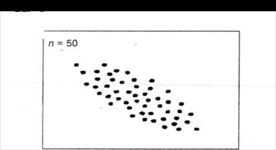
Рисунок 4.18в.Обратная (отрицательная) корреляция
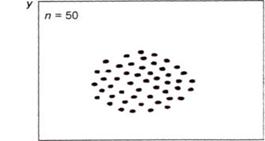 |
Рисунок 4.18г.Лёгкая обратная корреляция
Рисунок 4.18д.Отсутствие корреляции
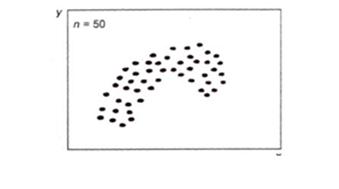
Рисунок 4.18ж.Криволинейная корреляция
Диаграммы разброса представляют из себя графики, которые позволяют выявить корреляцию (статистическую зависимость) между различными факторами, влияющими на показатели качества. Диаграмма строится по двум координатным осям, по оси абсцисс откладывается значение изменяемого параметра, а на оси ординат откладывается получаемое значение исследуемого параметра, которое мы имеем в момент использование изменяемого параметра, на пересечении этих значений ставим точку. Собрав достаточно большое количество таких точек, мы можем делать анализ и вывод.
Приведём пример. На предприятии решили проводить занятия по основам менеджмента качества. Каждый месяц обучение проходило определенное количество рабочих. В январе обучение прошли 2 человека, в феврале 3 человека и т.д. В течение года количество обученных работников возрастало и к концу года достигло 40 человек. Руководство дало поручение службе качества отследить зависимость процента бездефектной продукции, предъявляемой с первого раза, количества поступающих на завод рекламаций на продукцию со стороны заказчиков и расхода электроэнергии в цеху от количества обученных рабочих. Была составлена таблица 4.5 данных по месяцам и построены диаграммы разброса (рис. 4.19, 4.20, 4.21).
Таблица 4.5 Зависимость процента бездефектной продукции, предъявляемой с первого раза, количества поступающих на завод рекламаций на продукцию и расхода электроэнергии в цеху от количества обученных рабочих
| Кол-во обученных рабочих | % бездефектности | Количество рекламаций | Расход энергии, кВт |
| Январь | |||
| Февраль | |||
| Март | |||
| Апрель | |||
| Май | |||
| Июнь | |||
| Июль | |||
| Август | |||
| Сентябрь | |||
| Октябрь | |||
| Ноябрь | |||
| Декабрь |
Количество обученных работников
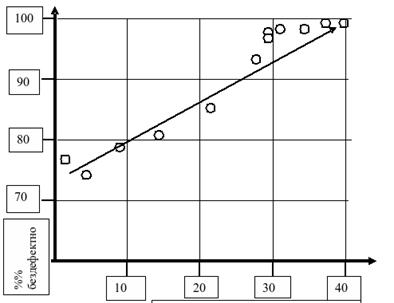
Рисунок 4.19 Зависимость процента бездефектности от количества
работников, прослушавших курс по основам менеджмента качества.
Количество обученных работников
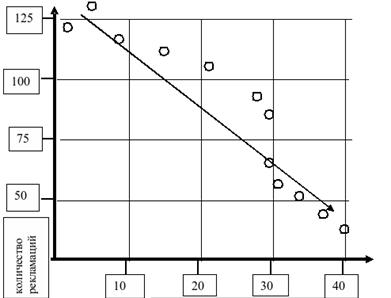
Рисунок 4.20 Зависимость числа рекламаций от количества работников, прослушавших курс по основам менеджмента качества.
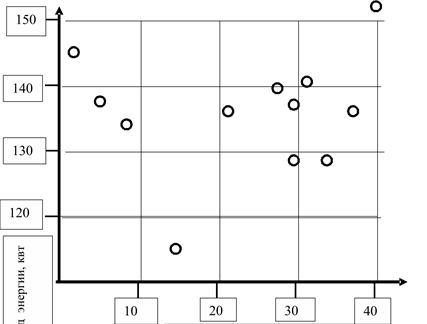
Количество обученных работников
Рисунок 4.21 Зависимость расхода энергии от количества работников, прослушавших курс по основам менеджмента качества.
На рисунках 4.19, 4.20 и 4.21 хорошо видно, что процент бездефектности повышается, имеем прямую корреляционную зависимость, количество рекламаций уменьшается, имеем обратную корреляционную зависимость, причем на диаграммах хорошо видна чётко выраженная корреляционная зависимость, которая определяется по кучности точек и их приближении к какой либо точно очерченной траектории, в нашем случае это прямая линия. Количество расходуемой электроэнергии не имеет зависимости от количества обученных работников.
Для сравнения информации о текущем состоянии процесса, полученной по выборке, с контрольными границами, являющимися пределами собственного разброса, применяют контрольные карты.
Контрольная карта- это графическое представление характеристики процесса, состоящее из центральной линии, контрольных границ и конкретных значений, имеющихся статистических данных позволяющее оценить степень статистической управляемости процесса.
Существует много разных типов контрольных карт в зависимости от природы данных, вида статистической обработки данных и методов принятия решений.
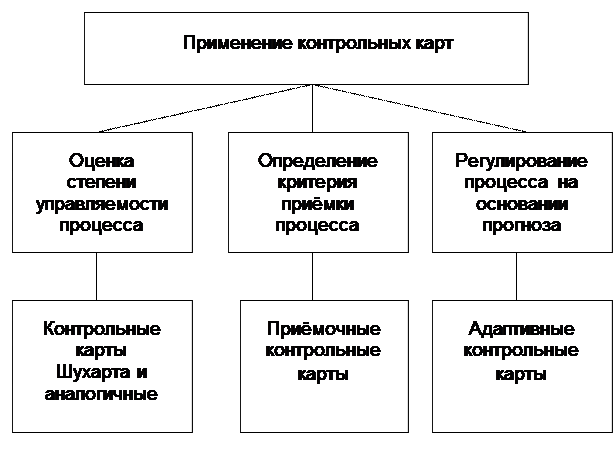
В зависимости от сферы применения выделяют три основных вида контрольных карт (рис. 4.22):
· контрольные карты Шухарта и аналогичные им, позволяющие оценить, находится ли процесс в статистически управляемом состоянии;
· приёмочные контрольные карты, предназначенные для определения критерия приёмки процесса;
· адаптивные контрольные карты, с помощью которых регулируют процесс посредством планирования его тренда (тенденции изменения процесса с течением времени) и проведения упреждающей корректировки на основании прогнозов.
Рисунок 4.22 Применение контрольных карт
Данные для контрольных карт разделяют на количественные и качественные.
Диаграмма рассеяния
Описание
Также известна как график рассеяния, точечный график, координатный график или скатерограмма.
На диаграммах рассеяния ряд точек, размещенных в декартовой системе координат, отображает значения по двум переменным. Присвоив каждой оси переменную, можно определить, существуют ли отношения или корреляция между этими двумя переменными.
Отображаемые на диаграммах рассеяния паттерны позволяют увидеть разные типы корреляции. Среди них: положительная (оба значения увеличиваются), отрицательная (одно значение увеличивается, в то время как второе уменьшается), нулевая (отсутствие корреляции), линейная, экспоненциальная и подковообразная. Сила корреляции определяется по тому, насколько близко расположены друг от друга точки на графике. Точки, которые значительно удалены от общего кластера точек, называются выбросами.
На графике могут использоваться линии или кривые, которые помогают при анализе и проводятся максимально близко ко всем точкам, чтобы продемонстрировать, как бы все эти точки могли потенциально выстроиться в одну линию. Этот элемент известен под названием «линия наилучшего соответствия» или «линия общего направления» и может использоваться для оценки через интерполяцию.
Диаграммы рассеяния идеально подходят в том случае, если у вас есть пара числовых данных, и вы хотите посмотреть, существует ли влияние одной переменной на другую. Однако не забывайте, что корреляция – это не причинная зависимость, поэтому на результаты может повлиять не принятая во внимание переменная.
Диаграмма рассеяния
Диаграмма рассеяния (также точечная диаграмма, англ. scatter plot ) — математическая диаграмма, изображающая значения двух переменных в виде точек на декартовой плоскости.
На диаграмме рассеяния каждому наблюдению (или элементарной единице набора данных) соответствует точка, координаты которой (в декартовой системе координат) равны значениям двух каких-то параметров этого наблюдения. Если предполагается, что один из параметров зависит от другого, то обычно значения независимого параметра откладывается по горизонтальной оси, а значения зависимого — по вертикальной. Диаграммы рассеяния используются для демонстрации наличия или отсутствия корреляции между двумя переменными.
Литература
Полезное
Смотреть что такое «Диаграмма рассеяния» в других словарях:
ДИАГРАММА РАССЕЯНИЯ — (scatter diagram) Диаграмма, описывающая соотношение между двумя характеристиками различных субъектов – частных лиц, фирм или стран. Каждая точка, отмеченная на диаграмме, включает две характеристики, например возраст и доход индивида, отложенные … Экономический словарь
диаграмма рассеяния — Полезный способ визуализации множества двух или трехмерных данных (совместного распределения двух или трех переменных). На ней каждому наблюдению соответствует одна точка, по осям откладываются значения переменных, точки на диаграмме не соединены … Словарь социологической статистики
ДИАГРАММА РАССЕЯНИЯ — двумерный график для изображения совместного распределения двух количественных переменных ( также Шкала измерительная). Каждый объект из выборки представляется в виде точки, координатами которой служат соответствующие ему значения двух переменных … Социология: Энциклопедия
Диаграмма рассеяния — график, в суммарном виде отражающий распределение признаков относительно двух переменных с использованием пунктира для обозначения результатов наблюдений … Социологический словарь Socium
Диаграмма Исикавы — Диаграмма Исикавы т. н. диаграмма «рыбьей кости» (англ. Fishbone Diagram) или «причинно следственная» диаграмма (англ. Cause and Effect Diagram), а также как диаграмма «анализа корневых причин». Один из семи основных… … Википедия
Диаграмма разброса д рассеяния — Диаграмма разброса, д. рассеяния * дыяграма роскіду, д. рассеяння * scatter diagram диаграмма, на которой полученные величины нанесены в системе координат х и у с целью определения, есть ли корреляция (см.) между этими величинами (напр., между… … Генетика. Энциклопедический словарь
Диаграмма рассеивания — Графическое изображение корреляции между двумя сериями измерений к примеру, между коэффициентом умственного развития и оценками на зкзаменах. Чем больше точек на диаграмме рассеяния образует определенную тенденцию, тем выше степень корреляции.… … Большая психологическая энциклопедия
Диаграмма разброса
Применяется диаграмма разброса в том случае, когда необходимо отобразить что происходит с одной переменной при изменении другой, для определения причины возникновения неконтролируемых точек в ходе многовариантного статистического контроля процесса, подтверждения взаимосвязи, выявленной в результате применения причинно-следственной диаграммы (диаграммы Исикавы) и пр.
Диаграмма разброса строится в следующей последовательности:
1. Собираются парные данные, которые по предположению являются взаимосвязанными. Желательно, чтобы таких парных данных было не менее 20-25. Это позволит более объективно установить зависимость между данными.
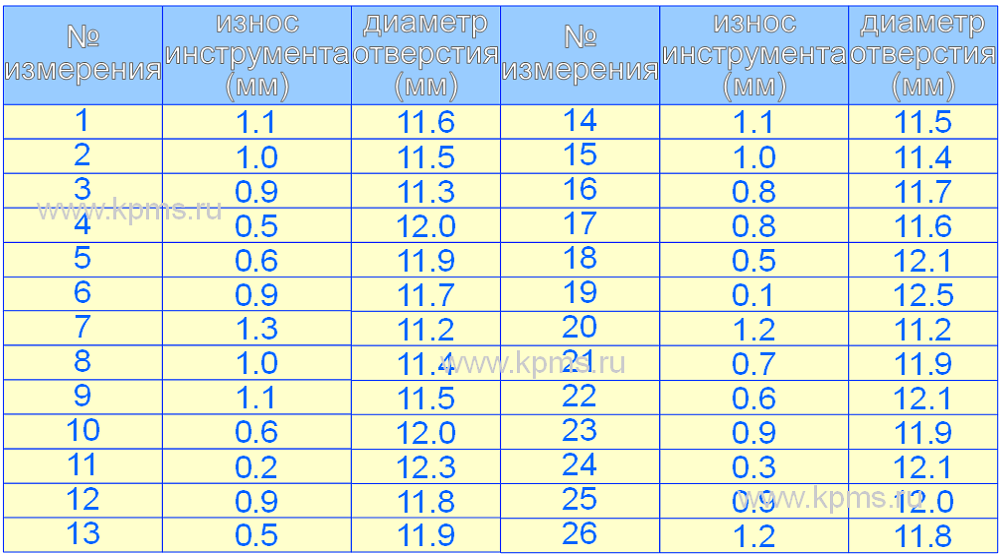
2. Составляется список данных. В списке данных для каждого измерения по порядку указываются значения парных данных.
3. Определяются максимальные и минимальные значения по каждому из типов парных данных.
4. Выбираются шкалы для осей диаграммы разброса на основании разницы между максимальным и минимальным значением каждого из типов парных данных. При необходимости (если отображаемые величины имеют малые размеры) могут применяться коэффициенты масштабирования шкалы.
6. На диаграмму наносятся парные данные. Если для разных измерений получаются одинаковые значения данных, то для отделения данных друг от друга используется другое обозначение (например, точки и треугольники) или данные обозначаются рядом друг с другом.
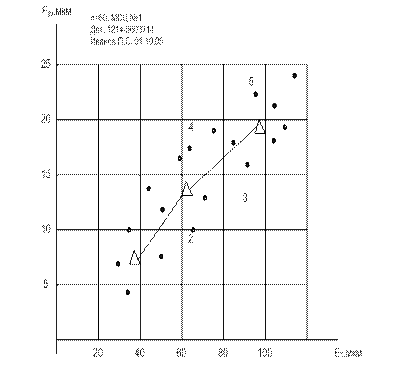
Пример
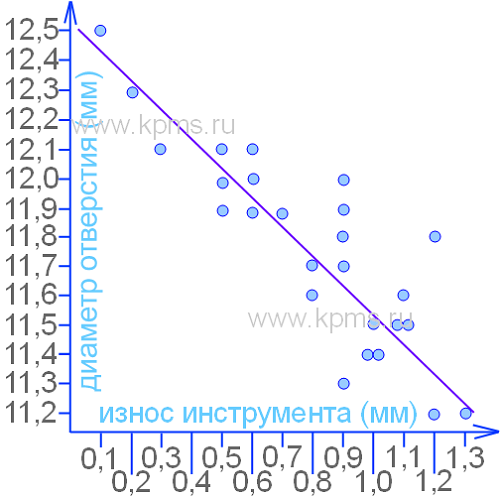
Диаграмма разброса построена для парных данных – «износ инструмента» и «диаметр отверстия». Данные собирались, чтобы показать влияние износа инструмента на диаметр отверстия. Как предполагалось, чем больше износ инструмента, тем меньше должен быть диаметр отверстия.
Величина шкалы, на которой будут отображаться данные – 1,2 мм. Для отображения данных на диаграмме применим коэффициент масштабирования 10.
Величина шкалы, на которой будут отображаться данные – 1,7 мм. Для отображения данных на диаграмме применим коэффициент масштабирования 10.
Между точками на графике можно провести прямую линию, вдоль которой они концентрируются. Это свидетельствует о корреляции между исследуемыми парными данными. Диаграмма разброса показывается величину и наличие взаимосвязи между двумя переменными. Направление и «сжатость» кластера точек говорит о виде и силе взаимосвязи между двумя переменными. Чем больше этот кластер имеет сходство с прямой линией, тем сильнее корреляция между парными данными.
На основании проведенного анализа, который предоставляет диаграмма разброса, можно принимать дальнейшие решения. В частности, для приведенного примера можно установить допустимый предел износа инструмента в зависимости от разрешенного допуска на диаметр отверстия.
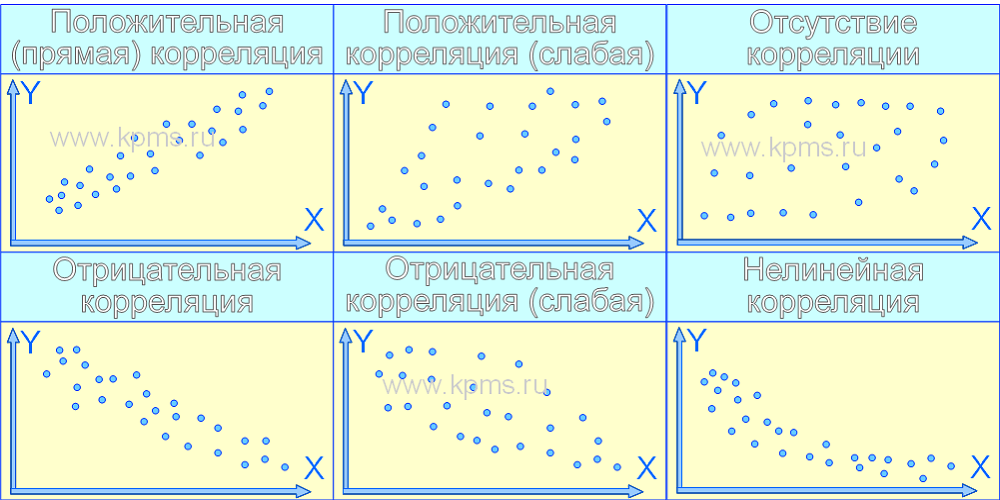
Варианты корреляции
Форма и расположение кластера точек на диаграмме разброса определяют различные варианты корреляции парных данных. Наиболее часто встречающиеся из них приведены на рисунках ниже.
Диаграмма разброса является удобным и простым инструментом для выявления взаимосвязи парных данных. Однако сильная взаимосвязь не обязательно означает, что одна переменная напрямую связана с другой переменной. В частности, может быть третья переменная, которая влияет на исследуемые парные данные и которая в итоге «кластеризует» точки на диаграмме разброса.
Инструмент «диаграмма разброса» входит в состав сборника «Семь инструментов качества». Сборник можно приобрести в интернет-магазине «Менеджмент качества».
Семь инструментов качества
Семь инструментов качества
Брошюра «Семь инструментов качества» содержит справочную информацию об основных инструментах менеджмента качества. В брошюре представлено описание и даны примеры применения следующих инструментов менеджмента качества: