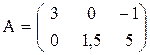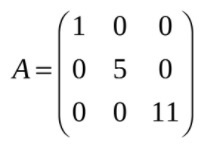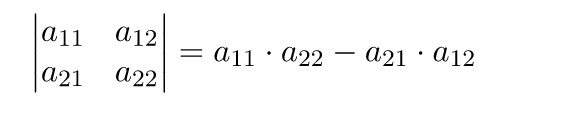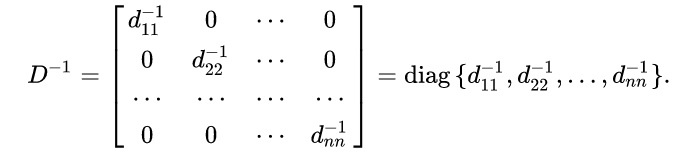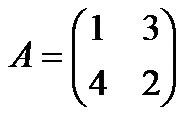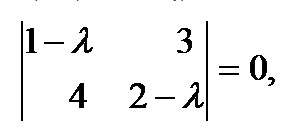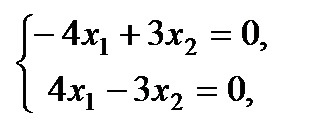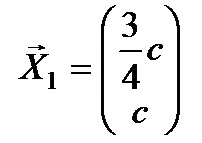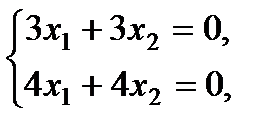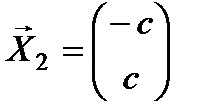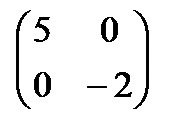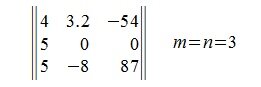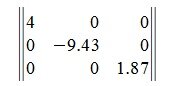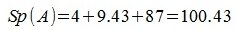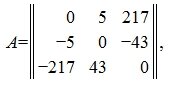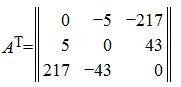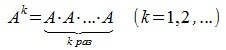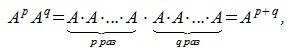Что такое диагональные элементы матрицы

Матрицы

Линейная алгебра

Матрица размера m х n – это прямоугольная таблица чисел, содержащая m строк и n столбцов. Числа, составляющие матрицу, называются элементами матрицы.

Матрицы принято обозначать заглавными латинскими буквами, а элементы – теми же, но строчными буквами с двойной индексацией.

Например, рассмотрим матрицу А размерности 2 х 3:

Матрицы А и В одного размера (m х n ) называют равными, если они поэлементно совпадают, т.е. a_ij = b_ij для , т.е. для любых i и j (можно записать «i, j).

Матрица-строка – это матрица, состоящая из одной строки, а матрица-столбец – это матрица, состоящая из одного столбца.

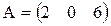
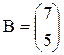
Например, — матрица-строка, а .

Квадратная матрица n-го порядка – это матрица, в число строк равно числу столбцов и равно n.

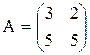
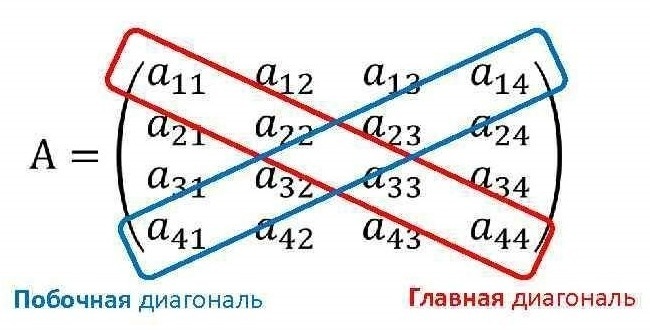
Например, — квадратная матрица второго порядка.

Диагональные элементы матрицы – это элементы, у которых номер строки равен номеру столбца (a_ij, i = j). Эти элементы образуют главную диагональ матрицы. В предыдущем примере главную диагональ образуют элементы a₁₁= 3 и a₂₂= 5.

Диагональная матрица – это квадратная матрица, в которой все недиагональные элементы равны нулю. Например, — диагональная матрица третьего порядка. Если при этом все диагональные элементы равны единице, то матрица называется единичной (обычно обозначаются буквой Е). Например, — единичная матрица третьего порядка.

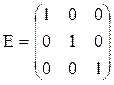
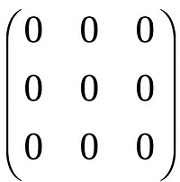
Матрица называется нулевой, если все ее элементы равны нулю.

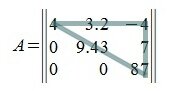
Квадратная матрица называется треугольной, если все ее элементы ниже (или выше) главной диагонали равны нулю. Например, 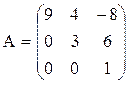— треугольная матрица третьего порядка.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Диагональные матрицы: определение и свойства

Обновлено: 20 Июля 2021

Матрица — это прямоугольная таблица чисел, состоящая из определенного количества строк и столбцов. Существует множество матричных видов, и один из них — диагональный. Разберемся, что он из себя представляет.

Что такое диагональная матрица

У диагональной матрицы элементы, расположенные вне главной диагонали, равны нулю.

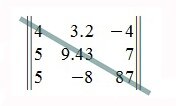
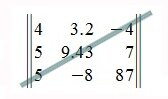
Напомним, что матрица считается квадратной, если количество строк равно количеству столбцов (m = n).

Особенности и свойства

Для начала нужно понять, что такое матричный определитель.

Определитель (детерминант) — это некоторая величина, с которой можно сопоставить любую квадратную матрицу.

Определитель А = (2×2), к примеру, вычисляется по формуле:

Из этого следует свойство №1: определитель диагональной матрицы равен произведению ее диагональных элементов.

Свойство №2: обратная матрица для диагональной равна:

Свойство №3: ранг равен количеству ненулевых диагональных элементов.

Главная и побочная диагонали

Побочной диагональю называют диагональ элементов от правого верхнего угла до нижнего левого. Эти диагонали параллельны друг другу.

Частные случаи диагональных матриц

Существуют три основных подвида: единичная, нулевая, скалярная.

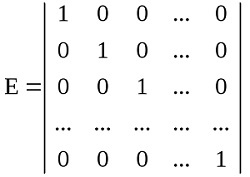
Единичная матрица

У единичной матрицы все диагональные элементы равны единице.

В формулах ее обозначают буквой Е.

Нулевая матрица

В нулевой матрице все элементы, в том числе диагональные, равны нулю.

В формулах ее обозначают цифрой 0.

Скалярная матрица

В скалярной матрице все элементы на главной диагонали равны друг другу.

В некоторых случаях говорят, что скалярная матрица — это произведение скаляра на единичную матрицу Е. В ней диагональные элементы могут быть как положительными, так и отрицательными.

Примеры решения диагональных матриц

Иногда недиагональная матрица может быть приведена к диагональному виду.

Условие: дана матрица А

Задача: привести к диагональному виду.

Решение: характеристическое уравнение равно

Таким образом, диагональная матрица имеет вид:

Изучение данных математических объектов имеет свои подводные камни. Если у вас нет времени на учебу, Феникс.Хелп может помочь вам с решением контрольных, самостоятельных и иных проверочных работ.

Источник

Матрицы. Виды матриц

Матрицей называется прямоугольная таблица из чисел с некоторым количеством m строк и с некоторым количеством n столбцов. Числа m и n называются порядками или размерами матрицы.

Матрица порядка m × n записывается в форме:

или (i=1,2. m; j=1,2. n).

Числа a_ij входящие в состав данной матрицы называются ее элементами. В записи a_ij первый индекс i означает номер строки, а второй индекс j— номер столбца.

Матрица строка

Матрица размером 1×n, т.е. состоящая из одной строки, называется матрицей-строкой. Например:

Матрица столбец

Матрица размером m×1, т.е. состоящая из одного столбца, называется матрицей-столбцом. Например

Нулевая матрица

Квадратная матрица

Матрица A порядка m×n называется квадратной матрицей, если количество строк и столбцов совпадают: m=n. Число m=n называется порядком квадратной матрицы. Например:

Главная диагональ матрицы

Побочная диагональ матрицы

Диагональная матрица

Квадратная матрица называется диагональной, если элементы, расположенные вне главной диагонали равны нулю. Пример диагональной матрицы:

Единичная матрица

След матрицы

Сумма главных диагональных элементов матрицы A называется следом матрицы и обозначается Sp A или Tr A. Например:

Верхняя треугольная матрица

Нижняя треугольная матрица

Квадратная матрица порядка n×n называется нижней треугольной матрицей, если равны нулю все элементы матрицы, расположенные над главной диагональю, т.е. a_ij=0, при всех i T ).

Cтолбцы матрицы A образуют пространство столбцов матрицы и обозначаются через R(A).

Ядро или нуль пространство матрицы

Противоположная матрица

Для любой матрицы A сущеcтвует противоположная матрица -A такая, что A+(-A)=0. Очевидно, что в качестве матрицы -A следует взять матрицу (-1)A, элементы которой отличаются от элементов A знаком.

Кососимметричная (Кососимметрическая) матрица

Кососимметричной называется квадратная матрица, которая отличается от своей транспонированной матрицы множителем −1:

В кососимметричной матрице любые два элемента, расположенные симметрично относительно главной диагонали отличаются друг от друга множителем −1, а диагональные элементы равны нулю.

Пример кососимметрической матрицы:

Разность матриц

Разностью C двух матриц A и B одинакового размера определяется равенством

Для обозначения разности двух матриц используется запись:

Степень матрицы

Пусть квадратная матрица размера n×n. Тогда степень матрицы определяется следующим образом:

где E-единичная матрица.

Из сочетательного свойства умножения следует:

где p,q— произвольные целые неотрицательные числа.

Симметричная (Симметрическая) матрица

Матрица, удовлетворяющая условию A=A T называется симметричной матрицей.

Для симметричных матриц имеет место равенство:

Источник

Виды матриц

Виды матриц не по зубам? Тебе ответит эксперт через 10 минут!

Диагональные матрицы

Замечание. Диагональные элементы матрицы (т.е. элементы, стоящие на главной диагонали) могут также равняться нулю.

Замечание. Если нулевая матрица является квадратной, то она также является и скалярной.

Треугольные матрицы

Матрица называется верхней треугольной матрицей, если все элементы ниже главной диагонали равны нулю.

Матрица называется нижней треугольной матрицей, если все элементы выше главной диагонали равны нулю.

Ступенчатая матрица

Ступенчатой называется матрица, удовлетворяющая следующим условиям:

Другое определение ступенчатой матрицы.

$$A=\left(\begin a_ <11>& a_ <12>& a_ <13>& \ldots & a_ <1 r>& \ldots & a_ <1 n>\\ 0 & a_ <22>& a_ <23>& \ldots & a_ <2 r>& \ldots & a_ <2 n>\\ 0 & 0 & a_ <33>& \ldots & a_ <3 r>& \ldots & a_ <3 n>\\ \ldots & \ldots & \ldots & \ldots & \ldots & \ldots & \ldots \\ 0 & 0 & 0 & \ldots & a_ & \ldots & a_ \\ 0 & 0 & 0 & \ldots & 0 & \ldots & 0 \\ \ldots & \ldots & \ldots & \ldots & \ldots & \ldots & \ldots \\ 0 & 0 & 0 & \ldots & 0 & \ldots & 0 \end\right)$$

Другое определение ступенчатой матрицы.

Примеры ступенчатых матриц:

Примеры матриц, которые не являются ступенчатыми:

Решение. Проверяем выполнение условий из определения:

Источник

Диагональную матрицу иногда называют матрица масштабирования, так как умножение матрицы на нее приводит к изменению масштаба (размера). Его определитель является произведением диагональных значений.

Содержание

Определение

Однако вход по главной диагонали неограничен.

Следующая матрица представляет собой квадратную диагональную матрицу:

В оставшейся части этой статьи мы будем рассматривать только квадратные диагональные матрицы и будем называть их просто «диагональными матрицами».

Скалярная матрица

Диагональная матрица, у которой все главные диагональные элементы равны, есть скалярная матрица, то есть скалярное кратное λI из единичная матрица я. Его влияние на вектор является скалярное умножение к λ. Например, скалярная матрица 3 × 3 имеет вид:

Векторные операции

Это математически эквивалентно, но позволяет избежать хранения всех нулевых членов этого разреженная матрица. Таким образом, этот продукт используется в машинное обучение, например, вычисление продуктов производных в обратное распространение или умножая веса IDF на TF-IDF, [2] поскольку некоторые BLAS структуры, которые эффективно умножают матрицы, не включают напрямую возможности продукта Адамара. [3]

Матричные операции

В частности, диагональные матрицы образуют подкольцо кольца всех п-от-п матрицы.

Операторная матрица в собственном базисе

Характеристики

В сопоставлять диагональной матрицы снова диагональной.

Квадратная матрица диагональна тогда и только тогда, когда она треугольная и нормальный.

Любая квадратная диагональная матрица также является симметричная матрица.

Симметричная диагональная матрица может быть определена как матрица, которая одновременно верхний и нижнетреугольный. В единичная матрица я_п и любой квадрат нулевая матрица диагональные. Одномерная матрица всегда диагональна.

Приложения

Диагональные матрицы встречаются во многих областях линейной алгебры. Из-за простого описания матричной операции и собственных значений / собственных векторов, приведенных выше, обычно желательно представить данную матрицу или линейная карта диагональной матрицей.

Фактически, данный п-от-п матрица А является аналогичный в диагональную матрицу (это означает, что существует матрица Икс такой, что Икс −1 ТОПОР диагональна) тогда и только тогда, когда она имеет п линейно независимый собственные векторы. Такие матрицы называются диагонализуемый.

Над поле из настоящий или сложный числа, правда больше. В спектральная теорема говорит, что каждый нормальная матрица является унитарно похожий к диагональной матрице (если AA ∗ = А ∗ А тогда существует унитарная матрица U такой, что UAU ∗ диагональный). Кроме того, разложение по сингулярным числам следует, что для любой матрицы А, существуют унитарные матрицы U и V такой, что БПЛА ∗ диагональна с положительными элементами.

Теория операторов

Источник