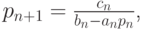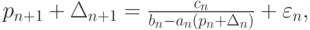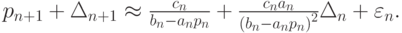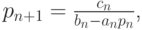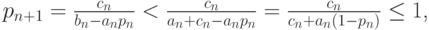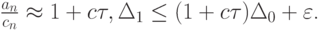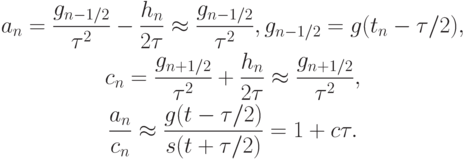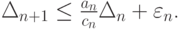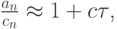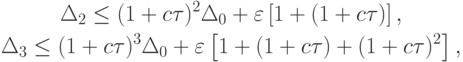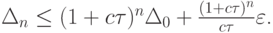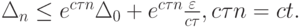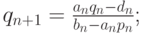Что такое диагональное преобладание

Диагональное преобладание

Говорят, что квадратная матрица обладает свойством диагонального преобладания, если

причем хотя бы одно неравенство является строгим. Если все неравенства строгие, то говорят, что матрица обладает строгим диагональным преобладанием.

Матрицы с диагональным преобладанием довольно часто возникают в приложениях. Их основное преимущество состоит в том, что итерационные методы решения СЛАУ с такой матрицей (метод простой итерации, метод Зейделя) сходятся к точному решению, которое существует и единственно при любых правых частях.

Свойства

См. также

Смотреть что такое «Диагональное преобладание» в других словарях:

Нистагм — I Нистагм (nystagmus; греч. nystagmos дремота) повторяющиеся (двусторонние, редко одно сторонние) толчкообразные, как правило, непроизвольные движения глазных яблок. Может возникать у здоровых людей, например при наблюдении за быстро движущимися… … Медицинская энциклопедия

Земля (планета) — Земля (от общеславянского зем пол, низ), третья по порядку от Солнца планета Солнечной системы, астрономический знак Å или, ♀. I. Введение З. занимает пятое место по размеру и массе среди больших планет, но из планет т. н. земной группы, в… … Большая советская энциклопедия

Земля — I Земля (от общеславянского зем пол, низ) третья по порядку от Солнца планета Солнечной системы, астрономический знак ⊕ или, ♀. I. Введение З. занимает пятое место по размеру и массе среди больших планет, но из планет т … Большая советская энциклопедия

СЕРДЦЕ — СЕРДЦЕ. Содержание: I. Сравнительная анатомия. 162 II. Анатомия и гистология. 167 III. Сравнительная физиология. 183 IV. Физиология. 188 V. Патофизиология. 207 VІ. Физиология, пат.… … Большая медицинская энциклопедия

Источник

Лекция 11: Численное решение краевых задач для систем обыкновенных дифференциальных уравнений

Для этого рассмотрим вычисление прогоночного коэффициента p_n (т.е. этап прямого хода прогонки). В идеальной арифметике этот коэффициент равен

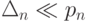
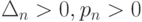
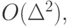
Полагая при 0, p_ > 0″ style=»display: inline; «> и опуская члены порядка получим оценку

Отсюда, учитывая, что

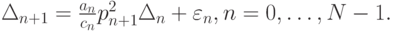( 10.2)

Докажем следующую теорему.

Докажем утверждение теоремы для случая, когда во всех строках матрицы выполнено условие строгого диагонального преобладания. На случай нестрогих неравенств обобщение доказательства очевидно.

Для этого вспомним выражения для коэффициентов линейной системы, полученной при разностной аппроксимации исходного уравнения второго порядка.

Вернемся к выражению для эволюции погрешности (10.2). С учетом полученных оценок имеем

Из цепочки неравенств

будет следовать оценка

При 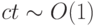погрешности не накапливаются (для краевых задач это реальное условие), поскольку в расчетах где — машинный эпсилон (подробнее в «Предмет вычислительной математики. Обусловленность задачи, устойчивость алгоритма, погрешности вычислений. Задача численного дифференцирования» ).

Аналогичное утверждение доказывается и для второго прогоночного коэффициента

Покажем устойчивость обратного хода прогонки.

Источник

Проверка возможности приведения к виду диагонального преобладания

Во многих курсах численных методов при рассмотрении методов простых итераций и Зейделя константируется что они будут сходиться если матрица коэф-тов будет иметь диагональное преобладание. Метод Гаусса тогда будет устойчив к погрешностям.
Можно ли придумать алгоритм проверки на возможность приведения к диагональному преобладанию.
За счет а)перемены уравнений(перестановки строк), б)переобозначения переменных(перестановка столбцов)
в)или за счет использования линейных комбинаций уравнений типа (1)->(3)-2*(1)
так чтобы на главных диагонали стояли максимальные по модулю элементы строк или столбцов.
Тогда это проверяется легко

Добавлено через 1 час 1 минуту
(Разумеется прямой ход метода Гаусса с выбором диагонального элемента удовлетворяет сфомулированным требованиям), но не хотелось бы делать алгоритм похожим на метод Гаусса и обнулять нижний треугольник матрицы, а сделать проше

Проверка возможности приведения к заданному типу, интерфейсу
Реализовать метод, который проверяет реализует ли входной параметр метода интерфейс.

Проверка условия преобладания диагональных элементов
Написать функцию, для проверки условия преоблада- ния диагональных элементов матрицы (см. метод.

Реализация алгоритма приведения кривой к каноническому виду
Помогите, прошу. Нужно написать програму для приведение кривой к каноническому виду. Алгоритм вроде.

Найти ошибку в процедуре приведения УрЧП к каноническому виду
Процедура для приведение УрЧП к каноническому виду. При запуске выдает ошибку Error, reserved word.

Источник