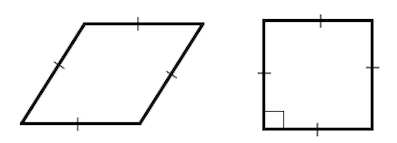Что такое диагональ ромба рисунок

Ромб. Свойства и признаки ромба

Ромб – это параллелограмм, у которого все стороны равны.

Если у ромба – прямые углы, то он называется квадратом.

Свойства ромба

1. Поскольку ромб – это параллелограмм, то все свойства параллелограмма верны для ромба.

Помимо этого:

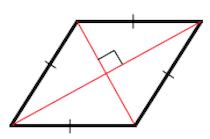
2. Диагонали ромба перпендикулярны.

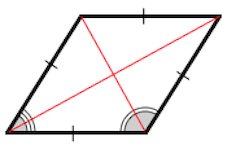
3. Диагонали ромба являются биссектрисами его углов.

4. Сумма квадратов диагоналей равна квадрату стороны, умноженному на 4.

Признаки ромба

Чтобы параллелограмм оказался ромбом, необходимо выполнение одного из следующих условий:

1. Все стороны параллелограмма равны между собой ().

2. Диагонали пересекаются под прямым углом ().

3. Диагонали параллелограмма являются биссектрисами его углов.

Площадь ромба

Смотрите также таблицу-шпаргалку «Площади простейших фигур» здесь.

Чтобы не потерять страничку, вы можете сохранить ее у себя:

Источник

Что такое ромб: определение, свойства, признаки

В данной публикации мы рассмотрим определение, свойства и признаки (с рисунками) одной из основных геометрических фигур – ромба.

Определение ромба

Ромб – это фигура на плоскости; разновидность параллелограмма, у которого все четыре стороны равны и попарно параллельны. Обычно ромб обозначается названиями его вершин (например, ABCD), а длина его стороны – строчной латинской буквой (например, a).

Примечание: квадрат является частным случаем ромба.

Свойства ромба

Свойство 1

Противоположные углы ромба равны между собой, а сумма соседних углов составляет 180°.

Свойство 2

Диагонали ромба пересекаются под прямым углом и в точке пересечения делятся пополам.

В результате пересечения диагоналей ромб делится на 4 прямоугольных треугольника: ΔAEB, ΔBEC, ΔAED и ΔDEC.

Свойство 3

Диагонали ромба являются биссектрисами его углов.

Свойство 4

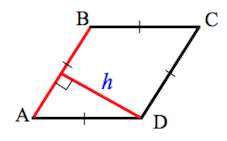
Сторону ромба a можно найти через его диагонали d₁ и d₂ (согласно теореме Пифагора).

Свойство 5

В любой ромб можно вписать окружность, центр которой лежит на пересечении его диагоналей.

Радиус вписанной в ромб окружности r вычисляется по формуле:

Признаки ромба

Параллелограмм является ромбом только в том случае, если для него верно одно из следующих утверждений:

Примечание: Любой четырехугольник, стороны которого равны, является ромбом.

Источник

Диагонали ромба

Поскольку ромб является одним из видов параллелограмма, то диагонали ромба в точке пересечения делятся пополам.

Кроме этого, диагонали ромба обладают другими свойствами.

(Свойство диагоналей ромба)

Диагонали ромба пересекаются под прямым углом.

Диагонали ромба являются биссектрисами его углов.

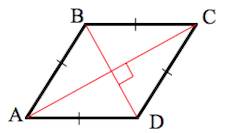
AC и BD — диагонали.

AC и BD — биссектрисы углов ромба.

Рассмотрим треугольник ABC.

Следовательно, треугольник ABC — равнобедренный с основанием AC (по определению равнобедренного треугольника).

Так как диагонали ромба в точке пересечения делятся пополам, то AO=OC.

Значит, BO — медиана треугольника ABC (по определению медианы).

Следовательно, BO — высота и биссектриса треугольника ABC (по свойству равнобедренного треугольника).

BD — биссектриса углов ABC (и ADC).

Из треугольника ABD аналогично доказывается, что AC — биссектриса углов BAD и BCD.

Что и требовалось доказать.

2 Comments

А оно надо так стараться?
Все маленькие треугольники равны по трем сторонам, следовательно углы посередине равны, получаем
4x = 360
x = 90
И про биссектрисы теорема сразу следует из равенства углов

Justifier, стараться надо всегда) Ваше доказательство вполне рабочее. Только надо каждый шаг обосновать. По длине окажется не короче приведенного выше. Геометрия тем и хороша, что доказать утверждение можно разными способами. Доказали по-своему — отлично!

Источник