Что такое диагональ многоугольника 8 класс
Вершины многоугольника называются соседними, если они являются концами одной из его сторон. Отрезки, соединяющие не соседние вершины многоугольника, называются диагоналями.
Многоугольник называется выпуклым если:
Определение I — для любых двух точек внутри него соединяющий их отрезок полностью лежит в нём.
Определение II — каждый внутренний угол меньше 180°.
Определение III — все его диагонали полностью лежат внутри него.
Определение IV – он лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины.
Сумма углов выпуклого n-угольника равна (n-2)∙180°.
Сумма углов невыпуклого n-угольника также равна (n-2)∙180°. (Доказательство аналогично, но использует в дополнение лемму о том, что любой многоугольник может быть разрезан диагоналями на треугольники).
Теорема: Число диагоналей всякого n-угольника равно 
Задача*: в каком выпуклом многоугольнике диагоналей на 25 больше чем сторон?
р = 25+n
25+n =
Разложим на множители
(n+5)(n-10)=0
n=-5 не удовлетворяет,
так как не существует
n = 10 удовлетворяет
Ответ: Десяти угольник.
Фигуры с равными диагоналями.*
Каждый четырехугольник имеет четыре вершины, четыре стороны и две диагонали.
Две несмежные стороны называются противоположными.
Две не соседние вершины называются противоположными.
1) Противоположные стороны параллелограмма равны. AB=DC, AD=BC.
2) Противоположные углы параллелограмма равны. ÐA=ÐC, ÐB=ÐD.
3) Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам. AO=OC, BO=OD.
4) Сумма углов, прилежащих к одной стороне, равна 180°. ÐA+ÐD=180°, ÐA+ÐB=180°, ÐB+ÐC=180°, ÐD+ÐC=180°.
5) Сумма всех углов равна 360°. ÐA+ÐB+ÐC+ÐD=360°.
6)* Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его двух смежных сторон: AC2+BD2=2∙(AB2+AD2).
Задача 1*: Найти диагональ параллелограмма, если известно, что длина одной диагонали равна AC=9 см, а стороны AD=7 см и AB=4 см.
Решение: Подставив значения в формулу получим:
BD2=49, следовательно вторая диагональ равна BD=7 см. Ответ: 7 см.
Задача 2*: Найти диагональ параллелограмма, если известно, что длина одной диагонали равна BD=10 см, а стороны AD=8 см и AB=2 см.
Решение: Условия задачи не верно, так как сумма двух сторон треугольника всегда больше третей стороны. Ответ: задача не имеет решений (смысла).
Задача 3*: а)Найти сторону параллелограмма, если известно, что длина диагоналей равна BD=6 см, AC=8, а одна сторона AB=5 см. б)Как называется этот параллелограмм.
Задача 4**: Сумма длин диагоналей параллелограмма равна 12 см, а произведение 32 найдите значение суммы квадратов всех его сторон.
Задача 5**:Найдите наибольший периметр параллелограмма, диагонали которого 6 см и 8 см.
Решение: Докажем, что среди всех параллелограммов с данными длинами диагоналей наибольший периметр имеет ромб.
Действительно, пусть a и b – длины соседних сторон параллелограмма, а 

Из равенства 
По неравенству между средним арифметическим и средним квадратичным: 


Определение 2: это четырёхугольник, у которого все углы прямые.
Определение 3: это параллелограмм, у которого один угол прямой.
Свойства прямоугольника: те же свойства, что и у параллелограмма +
1) Диагонали прямоугольника равны.
2)* Квадрат диагонали равен сумме квадратов сторон.
Задача 1: Меньшая сторона прямоугольника равна 5см, диагонали пересекаются под углом 60°. Найдите диагонали прямоугольника.
Задача 2: Меньшая сторона прямоугольника равна 24, диагонали пересекаются под углом 120°. Найдите диагонали и большую сторону прямоугольника.
Задача 3*: Сторона прямоугольника равна 3 см, диагональ 5 см. Найдите другую сторону прямоугольника.
Задача 4*: Сторона прямоугольника равна 6 см, диагональ 10 см. Найдите площадь прямоугольника.
Определение 2: это четырёхугольник, у которого все стороны равны.
Свойства ромба: те же свойства, что и у параллелограмма +
1) Диагонали ромба взаимно перпендикулярны (AC ⊥ BD).
3)*Сумма квадратов диагоналей равна квадрату стороны, умноженному на 4 (следствие из тождества параллелограмма).
Задача 1: Диагонали ромба 6 и 8 см. Найти сторону ромба.
Задача 2: Сторона ромба 10 см, один из углов 60°. Найти маленькую диагональ ромба.
Многоугольник
Определение 1. Многоугольник − замкнутая ломаная линия.
Объединение многоугольника и ограниченной им части плоскости также называют многоугольником. Поэтому представим другое определение многоугольника:
Определение 2. Многоугольник − это геометрическая фигура, которая является частю плоскости, ограниченная замкнутой ломаной.
Вершины ломаной называются вершинами многоугольника. Звенья ломаной называются сторонами многоугольника.
Любой многоугольник разделяет плоскость на две части, одна из которых называется внутренней областью многоугольника, а другая внешней областью многоугольника.
Виды многоугольников
Многоугольник с тремя вершинами называется треугольником, с четыремя вершинами − четырехугольником, с пяти вершинами − пятиугольником, и т.д. Многоугольник с \( \small n \) вершинами называется \( \small n- \)угольником.
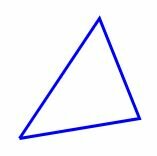 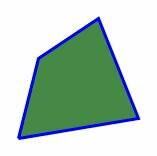 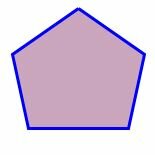  |
На рисунке 1 представлены различные виды многоугольников.
Обозначение многоугольника
Обозначают многоугольник буквами, стоящих при его вершинах. Называют многоугольник чередовав буквы при его вершинах по часовой стрелке или против часовой стрелки. Например, многоугольник на рисунке 2 называют \( \small A_1A_2A_3A_4A_5A_6 \) или \( \small A_6A_5A_4A_3A_2A_1 \).
Соседние вершины многоугольника
Вершины многоугольника называются соседними, если они являются концами одной из его сторон.
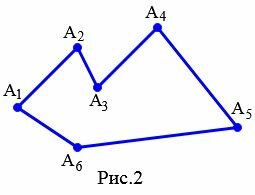 |
На рисунке 2 вершины \( \small A_2 \) и \( \small A_3 \) являются соседними, так как они являются концами стороны \( \small A_2A_3. \)
Смежные стороны многоугольника
Стороны многоугольника называются смежными, если они имеют общую вершину.
На рисунке 2 стороны \( \small A_4A_5 \) и \( \small A_5A_6 \) являются смежными, так как они имеют общую вершину \( \small A_5. \)
Простой многоугольник. Самопересекающийся многоугольник
Многоугольник называется простым, если его несмежные стороны не имеют общих точек (внутренних или концевых).
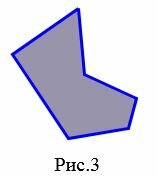 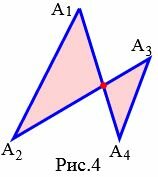 |
На рисунке 3 изображен простой многоугольник так как стороны многоугольника не имеют самопересечений. А на рисунке 4 многоугольник не является простым, так как стороны \( \small A_1A_4 \) и \( \small A_2A_3 \) пересекаются. Такой многоугольник называется самопересекающийся многоугольник.
Выпуклый многоугольник
Многоугольник называется выпуклым, если она лежит по одну сторону от прямой, проходящей через любую его сторону.
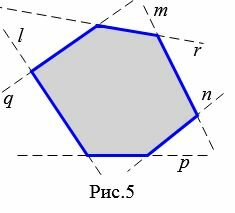 |
На рисунке 5 многоугольник лежит по одну сторону от прямых \( \small m, \ n, \ l, \ p, \ q, \ r\) проходящих через стороны многоугольника.
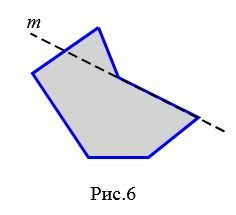 |
На рисунке 6 прямая \( \small m\) делит многоугольник на две части, т.е. многоугольник не лежит по одну сторону от прямой \( \small m\). Следовательно многоугольник не является выпуклым.
Правильный многоугольник
Простой многоугольник называется правильным, если все его стороны равны и все углы равны. Например равносторонний треугольник является правильным многоугольником, поскольку все его стороны равны, и все его углы равны 60°. Квадрат является правильным многоугольником, так как все его стороны равны и все его углы равны 90°.
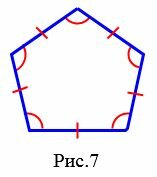 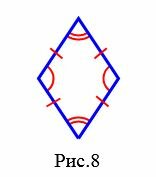 |
На рисунке 7 изображен правильный многоугольник (пятиугольник), так как у данного многоугольника все стороны равны и все углы равны. Многоугольник (ромб) на на рисунке 8 не является правильным, так как все стороны многоугольника равны, но все углы многоугольника не равны друг другу. Прямоугольник также не является правильным многоугольником, так как несмотря на то, что все углы прямоугольника равны, но все четыре стороны прямоугольника не равны друг другу.
Звездчатый многоугольник
Самопересекающийся многоугольник, все стороны которого равны и все углы равны, называется звездчатым или звездчато-правильным.
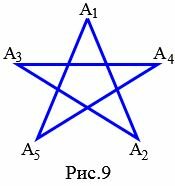 |
На рисунке 9 представлен звездчатый пятиугольник поскольку все углы \( \small A_1, \ A_2, \ A_3, \ A_4, \ A_5 \) равны и равны все стороны: \( \small A_1A_2=A_2A_3=A_3A_4=A_4A_5=A_5A_1. \)
Периметр многоугольника
Сумма всех сторон многоугольника называется периметром многоугольника. Для многоугольника \( \small A_1A_2. A_
Угол многоугольника
Углом (внутренним углом) многоугольника при данной вершине называется угол между двумя сторонами многоугольника, сходящимися к этой вершине. Если многоугольник выпуклый, то все углы многоугольника меньше 180°. Если же многоугольник невыпуклый, то он имеет внутренний угол больше 180° (угол \( \small A_3 \) на рисунке 2).
Внешний угол многоугольника
Внешним углом многоугольника при данной вершине называется угол смежный внутреннему углу многоугольника при данной вершине.
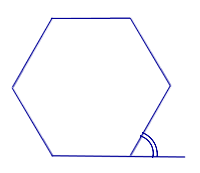
На рисунке 10 угол 1 является внешним углом данного многоугольника при вершине \( \small E. \)
Диагональ многоугольника. Количество диагоналей
Диагоналями называют отрезки, соединяющие две несоседние вершины многоугольника.
Выведем форулу вычисления количества диагоналей многоугольника. Пусть задан \( \small n \)-угольник. Выберем одну вершину многоугольника и проведем мысленно все отрезки, соединяющие эту вершину с остальными вершинами. Получим \( \small n-1 \) отрезков. Но поскольку две вершины для выбранной вершины являются соседними, а по определнию диагональ − это отрезок соединяющий несоседние вершины, то из \( \small n-1 \) вычтем 2. Получим \( \small n-3 \). Всего \( \small n \) вершин. Следовательно количество вычисленных диагоналей будет \( \small n(n-3). \) Учитывая, что каждый диагональ − это отрезок соединяющий две вершины, то получится, что мы вычислили каждый диагональ дважды. Поэтому полученное число нужно делить на два. Получим количество диагоналей \( \small n- \)мерного многоугольника:
Сумма углов выпуклого многоугольника
Выведем формулу вычисления суммы углов выпуклого многоугольника. Для этого проведем из вершины \( \small A_1 \) все диагноали многоугольника \( \small A_1A_2. A_
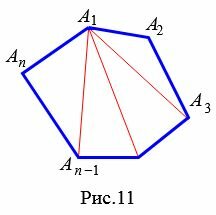 |
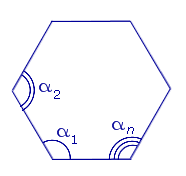
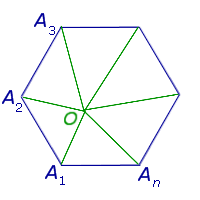
Количество диагоналей, проведенной из одной вершиы, как выяснили из предыдующего параграфа равно \( \small n-3 \). Следовательно, эти диагонали разделяют многоугольник на \( \small n-3+1=n-2 \) треугольников. Поскольку сумма углов треугольника равна 180°, то получим, что сумма углов выпуклого многоугольника равна: \( \small 180°(n-2). \)
где \( \small n \) −количество сторон (вершин) выпуклого многоугольника.
Угол правильного многоугольника
Поскольку у правильного многоугольника все углы равны, то используя формулу (1) получим угол правильного многоугольника:
где \( \small n \) −количество сторон (вершин) правильного многоугольника.
Многоугольники
 Определение многоугольника Определение многоугольника |
 Диагонали n – угольника Диагонали n – угольника |
 Внешний угол многоугольника Внешний угол многоугольника |
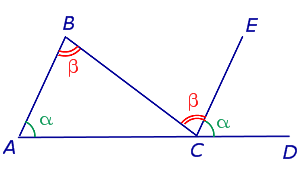
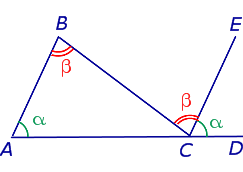
 Свойства углов треугольника Свойства углов треугольника |
 Свойства углов многоугольника Свойства углов многоугольника |
 Свойства углов правильного n – угольника Свойства углов правильного n – угольника |
 Доказательства теорем о свойствах углов многоугольника Доказательства теорем о свойствах углов многоугольника |
Определение многоугольника
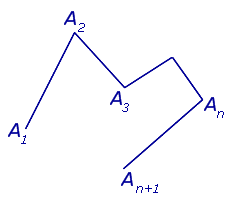
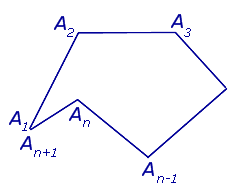
Рассмотрим n отрезков
причём таких, что два любых отрезка, имеющих общий конец, не лежат на одной прямой (рис.1).
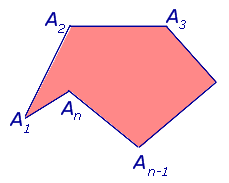
В случае, когда точки A1 и An +1 совпадают, ломаную линию называют замкнутой ломаной линией (рис. 2), в противном случае её называют незамкнутой (рис.1).
| Фигура | Рисунок | Описание | |||||||||||||||||
| Диагональ многоугольника | 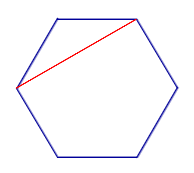 | Диагональю многоугольника называют отрезок, соединяющий две несоседние вершины многоугольника | |||||||||||||||||
| Диагонали n – угольника, выходящие из одной вершины | 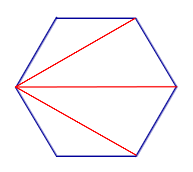 | Диагонали, выходящие из одной вершины n – угольника, делят n – угольник на n – 2 треугольника | |||||||||||||||||
| Все диагонали n – угольника | 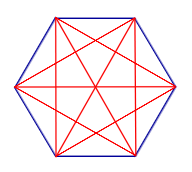 | ||||||||||||||||||
| Диагонали n – угольника, выходящие из одной вершины | |||||||||||||||||||
 Диагонали, выходящие из одной вершины n – угольника, делят n – угольник на n – 2 треугольника | |||||||||||||||||||
| Все диагонали n – угольника | |||||||||||||||||||
 Число диагоналей n – угольника равно Внешний угол многоугольникаСвойства углов треугольника
|





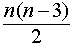




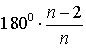
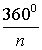
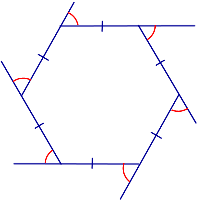
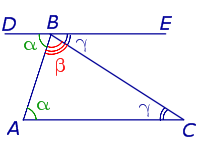
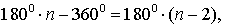










 — сумма углов стоугольника
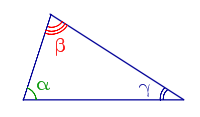
— сумма углов стоугольника — сумма углов треугольника
— сумма углов треугольника