Что такое диада триада и тетрада
Что такое диада, триада и тетрада. сколько двоичных разрядов они в себя включают?
Ответ:
2, 3, 4 разряда по условию
Объяснение:
Ответ:
2, 3 и 4 разряда соответственно
Объяснение:
От греческих Моно-1, Ди-2, Три-3, Тетра-4, Пента-5, Гекса-6, Гепта-7 и т.д.
Вот так даже правильнее
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
namespace NoNamespace
<
internal static class Program
<
private static void Main()
<
Console.WriteLine(«Введите n и m»);
var n = int.Parse(Console.ReadLine());
var m = int.Parse(Console.ReadLine());
if ((n r.Next(100));
Console.WriteLine(a.Print());
Console.WriteLine(a.Where(x => x%2 == 1).Print());
Console.WriteLine();
Console.WriteLine(@»Task2″);
var b = new int[n, m].ChangeEach(x => r.Next(-100, 100));
Console.WriteLine(b.Print());
Console.WriteLine(Task2(b).Print());
Console.WriteLine();
Console.WriteLine(@»Task3″);
Console.WriteLine(b.Print());
Console.WriteLine(b.Where(x => (x x > y);
var maxv = a[max.Item1, max.Item2];
a[max.Item1, max.Item2] = a[0, 0];
a[0, 0] = maxv;
public static class Extensions
<
public static List Where (this T[,] array, Func filter)
<
if (filter == null)
return null;
var list = new List ();
var sb = new StringBuilder(«Массив: «);
foreach (var ae in enumerable)
sb.Append($»
public static T[,] ChangeEach (this T[,] array, Func mutator)
<
if (mutator == null)
return array;
for (var i = 0; i (this T[] array, Func mutator)
<
if (mutator == null)
return array;
for (var j = 0; j (this T[,] a)
<
if (a.LongLength == 0)
return «Таких элементов нет»;
Семантический анализ. Внутреннее представление
Атрибутное дерево разбора
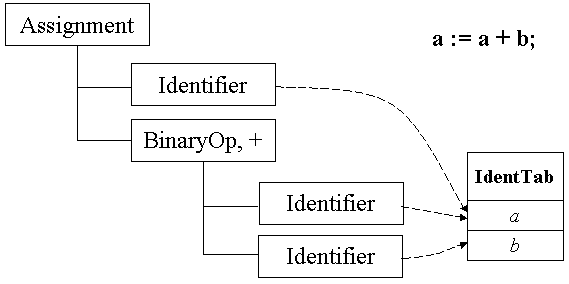
Атрибутное дерево разбора является, наверное, самой распространенной формой организации внутреннего представления программы. При таком подходе каждая исходная конструкция языка представляется в виде узла дерева, содержащего ссылки на все возможные элементы этой конструкции (естественно, каждый отдельный элемент тоже может иметь сложную структуру и, таким образом, также может быть поддеревом). Кроме того, каждый узел дерева может нагружаться дополнительными атрибутами, такими, как ссылки в таблицы представлений или таблицы идентификаторов. В итоге, вся программа представляется в виде единого дерева разбора.
На слайде в качестве примера приведено атрибутное дерево разбора, порожденное по следующему оператору исходного языка a := a + b; Отметим, что форма представления дерева, использованная на слайде, является типичной при компиляции, так как позволяет изобразить практически сколь угодно сложные деревья на экране компьютера (попробуйте представить себе традиционное изображение дерева разбора для сколько-нибудь сложной программы!).
Польская запись
Триады и тетрады
Триады и тетрады представляют собой низкоуровневые формализмы записи промежуточного представления программы, приближающие программу к объектному коду. В этих формализмах все операции записываются в виде последовательности действий, выдающих результаты.
Естественно, триады и тетрады также могут быть расширены для записи всех операций, поддерживаемых на данной целевой платформе.
Перевод из одной системы счисления в другую с помощью триад и тетрад
Развивающая – развивать познавательный интерес учащихся, умения применять полученные знания на практике.
Воспитательная – повысить уровень информационной культуры учащихся.
I. Проверка домашнего задания
Вызывается ученик к доске для выполнения домашнего упражнения
II. Изучение нового материала
Так как основания 8-1 и 16-й СС являются степенями двойки, то перевод чисел из этих СС в 2-ую и наоборот прост и основан на методах триад и тетрад. Число делится на триады (тетрады) вправо и влево от десятичной точки. Если крайние триады (тетрады) оказались неполными, они дополняются нулями.
| Алфавит | Триады | Тетрады |
| 0 | 000 | 0000 |
| 1 | 001 | 0001 |
| 2 | 010 | 0010 |
| 3 | 011 | 0011 |
| 4 | 100 | 0100 |
| 5 | 101 | 0101 |
| 6 | 110 | 0110 |
| 7 | 111 | 0111 |
| 8 | 1000 | |
| 9 | 1001 | |
| А(10) | 1010 | |
| В(11) | 1011 | |
| С(12) | 1100 | |
| D(13) | 1101 | |
| E(14) | 1110 | |
| F(15) | 1111 |
Упражнение: Выполнить перевод, используя тетрады и триады:
IV. Самостоятельная работа
Выполнить перевод, используя тетрады и триады:
Теоретический материал «Двоично-кодированные системы»
2.10. Двоично-кодированные системы
В двоично-кодированных системах счисления каждая цифра числа записывается двоичными числами, т.е. в двоичную систему переводится не само число, а его цифры, или, иными словами, они кодируются в двоичном виде. Для примера возьмем десятичное число 135.
В двоично-кодированном виде с помощью тетрад оно будет иметь вид
Но это не значит, что обратный перевод позволит получить исходное число, если вы переведете полученное двоичное число не по цифрам, а целиком. Действительно,
Для перевода этого же двоичного числа в восьмеричную систему распишем его по триадам, тогда
Проверим переводом в десятичную систему:
325,55 8 =5*8 0 +2*8 1 +3*8 2 +5*8 1 +5*8 2 =5+16+192+0,625+0,0781=213,7031 10.
Теперь переведем наше двоичное число в 16-ричную систему, для чего распишем его по тетрадам
Для проверки переведем полученный результат в десятичную систему:
Для двоично-кодированных систем, каждая цифра которых представлена полным набором комбинаций двоичных разрядов, закономерности представления и перевода вполне очевидны и просты.
1. Назовите двоично-кодированные системы, цифры которых кодируются всеми комбинациями данного количества двоичных разрядов.
2. Как связаны двоичные коды для представления чисел в 8- и 16-ричныхсистемах счисления с помощью триад и тетрад?
3. Как называется элемент, который хранит 1 бит информации в компьютерах в качестве основного носителя информации?
4. Что называется регистром?
5. Что такое диада, триада и тетрада? Сколько двоичных разрядов они включают в себя?
П-Т Проектное задание
Подготовьте раздел «Почему именно двоичная система счисления нашла широкое применение в компьютерной технике?» для реферата «Двоичное кодирование и компьютер».
Метод триад и тетрад



Для представления одной цифры 8-чной системы используется три двоичных разряда (триада).
| 8-ичная цифра | 10-тичная цифра | Триада | 8-ичная цифра | 10-тичная цифра | Триада |
Тогда для перевода восьмеричного числа в двоичную систему достаточно заменить каждую восьмеричную цифру соответствующей ей двоичной комбинацией из таблицы и избавиться при необходимости от незначащих нулей впереди, например:
Обратный перевод из двоичной системы в восьмеричную заключается в выделении троек двоичных цифр, начиная с конца двоичного числа и добавлении нулей слева для последней тройки, если в ней меньше трех цифр, например:
10101011002 = 1 010 101 1002 = 001 010 101 1002 = 12548
Для представления одной цифры 16-чной системы используется четыре двоичных разряда (тетрада).
| 16-ичная цифра | 10-тичная цифра | Тетрада | 16-ичная цифра | 10-тичная цифра | Тетрада |
| A | |||||
| B | |||||
| C | |||||
| D | |||||
| E | |||||
| F |
Алгоритмы перевода из 16-ричной системы в двоичную аналогичны алгоритмам метода триад с той лишь разницей, что в заменах участвуют не тройки, а четверки двоичных разрядов согласно таблице.
2A97C16 = 0010 1010 1001 0111 11002 = 1010101001011111002
Наиболее удобным способом перевода чисел из восьмеричной системы счисления в 16-ричную и обратно является перевод через двоичную систему. Так, чтобы представить некоторое восьмеричное число в 16-ричной системе, надо сначала по методу триад перевести его в двоичный вид, а затем полученное двоичное число при помощи метода тетрад перевести в 16-ричное. Неполную триаду дополняем слева нулями до полной.
DECA16 = 1101 1110 1100 10102 = 001 101 111 011 001 0102 = 1573128
Аналогично осуществляется перевод чисел из 8-ричной системы счисления в 16-ричную и обратно через двоичную систему. Так, чтобы представить некоторое шестнадцатеричное число в 8-ричной системе, надо сначала по методу тетрад перевести его в двоичный вид, а затем полученное двоичное число при помощи метода триад перевести в 8-ричное. Неполную тетраду дополняем слева нулями до полной.
741528 = 111 100 001 101 0102 = 0111 1000 0110 10102 = 786А16.