Что такое децибел в радиосвязи

Что такое децибел

Очень часто новички сталкивается с таким понятием, как децибел. Многие из них интуитивно догадываются, что это такое, но у большинства до сих пор возникают вопросы.

Что такое децибел?

Относительные логарифмические единицы Белы (децибелы) широко используются при количественных оценках параметров различных аудио, видео, измерительных устройств. Физическая природа сравниваемых мощностей может быть любой — электрической, электромагнитной, акустической, механической, — важно лишь, чтобы обе величины были выражены в одинаковых единицах — ваттах, милливаттах и т. п. Бел выражает отношение двух значений энергетической величины десятичным логарифмом этого отношения, причем под энергетическими величинами понимаются: мощность, энергия.

Кстати, эта единица получила свое название в честь Александра Белл (1847 — 1922) — американского ученого шотландского происхождения, основоположника телефонии, основателя всемирно известных компаний AT&T и «Bell Laboratories». Еще интересно напомнить, что во многих современных мобильных телефонах (смартфонах) обязательно есть выбираемый звук звонка (оповещения), так и называемый «bell». Впрочем, Бел относится к единицам, не входящим в Международную систему единиц (СИ), но в соответствии с решением Международного комитета мер и весов допускается к применению без ограничений совместно с единицами СИ. В основном применяется в электросвязи, акустике, радиотехнике.

Формулы для вычисления децибелов

P₁ — мощность до усиления, Вт

P₂ — мощность после усиления или ослабления, Вт

На практике, оказалось, что удобнее пользоваться уменьшенным в 10 раз значением Бел, т.е. децибел, поэтому:

дециБел (дБ) = 10 * lg(P2/P1)

Усиление или ослабление мощности в децибелах выражается формулой:

N_дБ — усиление, либо ослабление мощности в децибелах

P₁ — мощность до усиления, Вт

P₂ — мощность после усиления или ослабления, Вт

Значения Бел, децибел могут быть со знаком «плюс», если P2 > P1 (усиление сигнала) и со знаком «минус», если P2

Во многих случаях, сравнение сигналов путем измерения мощностей может быть неудобным или невозможным — проще измерить напряжение или ток.
В этом случае, если мы сравниваем напряжения или токи, формула примет уже другой вид:

N_дБ — усиление, либо ослабление мощности в децибелах

U₁ — это напряжение до усиления, В

U₂ — напряжение после усиления, В

I₂ — сила тока после усиления, А

Вот небольшая табличка, в которой приведены основные отношения напряжений и соответствующее число децибел:

Дело в том, что операции умножения и деления над числами в обычном базисе, заменяются операциями сложения и вычитания в логарифмическом базисе. Например, у нас есть два каскадно-включенных усилителя с коэффициентами усиления K1 = 963 и K2 = 48. Какой общий коэффициент усиления? Правильно — он равен произведению K = K1 * K2. Вы можете в уме быстро вычислить 963*48? Я — нет. Я могу прикинуть K = 1000*50 = 50 тыс., не более. А, если нам известно, что K1 = 59 дБ и K2 = 33 дБ, то К = 59+33 = 92 дБ — сложить было не трудно, надеюсь.

Закон Вебера-Фехнера

Почему именно децибелы? Все исходит от закона Вебера-Фехнера, который говорит нам, что интенсивность ощущения человеческих чувств прямо-пропорциональна логарифму интенсивности какого-либо раздражителя.

Так светильник, в котором восемь лампочек, кажется нам настолько же ярче светильника из четырёх лампочек, насколько светильник из четырёх лампочек ярче светильника из двух лампочек. То есть количество лампочек должно увеличиваться каждый раз вдвое, чтобы нам казалось, что прирост яркости постоянен. То есть если добавить к нашим 32 лампочкам на графике еще одну лампочку, то мы даже и не заметим разницы. Для того, чтобы для нашего глаза была заметна разница, мы должны к 32 лампочкам добавить еще 32 лампочки, и т.д. Или иными словами, для того, чтобы нам казалось, что наш светильник плавно набирает яркость, нам надо зажигать вдвое больше лампочек каждый раз, чем было предыдущее значение.

Поэтому децибел действительно удобнее в некоторых случаях, так как сравнивать две величины намного проще в маленьких цифрах, чем в миллионах и миллиардах. А так как электроника — это чисто физическое явление, то и децибелы не обошли ее стороной.

Децибелы и АЧХ усилителя

Как вы помните в прошлом примере с ОУ, у нас неинвертирующий усилитель усиливал сигнал в 10 раз. Если посмотреть в нашу табличку, то это получается 20 дБ относительно входного сигнала. Ну да, так оно и есть:

Также в дБ на некоторых графиках АЧХ обозначают наклон характеристики АЧХ. Это может выглядеть примерно вот так:

Давайте рассмотрим пример. Имеем фильтр высоких частот (ФВЧ) первого порядка, собранного на RC-цепи.

Его АЧХ будет выглядеть следующим образом (кликните для полного открытия)

Итак возьмем первую точку на частоте в 10 Герц. На частоте в 10 Герц амплитуда сигнала уменьшилась на 44 дБ, это видно в правом нижнем углу (out:-44)

Умножаем частоту на 10 (декада) и получаем вторую точку в 100 Герц. На частоте в 100 Герц наш сигнал уменьшился приблизительно на 24 дБ

Что еще измеряют в децибелах?

U_c — это эффективное значение напряжения сигнала, В

U_ш — эффективное значение напряжения шума, В

Чем выше значение сигнал/шум, тем более чистый звук обеспечивается аудиосистемой. Для музыкальной аппаратуры желательно, чтобы это отношение было не менее 75 дБ, а для Hi-Fi аппаратуры не менее 90 дБ. Не имеет значение физическая природа сигнала, важно, чтобы единицы были в одинаковых измерениях.

В качестве единицы логарифмического отношения двух одноимённых физических величин применяется также непер (Нп) — 1 Нп

0,8686 Б. В основе лежит не десятичный (lg), а натуральный (ln) логарифм отношений. В настоящее время используется редко.

Во многих случаях, удобно сравнивать между собой не произвольные величины, а одну величину относительно другой, названной условно опорной (нулевой, базовой).
В электротехнике, в качестве такой опорной или нулевой величины выбрано значение мощности равное 1 мВт выделяемое на резисторе сопротивлением 600 Ом.
В этом случае, базовыми значениями при сравнении напряжений или токов станут величины 0.775 В или 1.29 мА.

Для звуковой мощности такой базовой величиной является 20 микроПаскаль (0 дБ), а порог +130 дБ считается болевым для человека:

Более подробно об этом написано в Википедии по этой ссылке.

Для случаев когда в качестве базовых значений используются те или иные конкретные величины, придуманы даже специальные обозначения единиц измерений:

dbW (дБВт) — здесь отсчет идет относительно 1 Ватта (Вт). Например, пусть уровень мощности составил +20 дБВт. Это значит что мощность увеличилась в 100 раз, то есть на 100 Вт.

dBm (дБм) — здесь у нас отсчет уже идет относительно 1 милливатта (мВт). Например, уровень мощности в +30дБм будет соответственно равен 1 Вт. Не забываем, что это у нас энергетические децибелы, поэтому для них будет справедлива формула

Следующие характеристики — это уже амплитудные децибелы. Для них будет справедлива формула

dBV (дБВ) — как вы догадались, опорное напряжение 1 Вольт. Например, +20дБВ даст — это 10 Вольт

От дБВ также вытекают другие виды децибелов с разными приставками:

dBmV (дБмВ) — опорный уровень 1 милливольт.

dBuV (дБмкВ) — опорное напряжение 1 микровольт.

Здесь я привел наиболее употребимые специальные виды децибелов в электронике.

Децибелы используются и в других отраслях, где они также показывают отношение каких-либо двух измеряемых величин в логарифмическом масштабе.

Также на YouTube есть интересное видео о децибелах.

Источник

О децибелах для радиоинженеров

Узнайте о децибелах и их вариациях в контексте радиочастотного проектирования и тестирования.

Радиотехника, как и все научные дисциплины и подразделы, включает в себя довольно много специализированной терминологии. Одним из наиболее важных слов, которые вам понадобятся при работе в мире радиочастот, является «дБ» (и некоторые его варианты). Если вы глубоко закрепились в проектировании радиочастотных систем, то можете обнаружить, что слово «дБ» становится вам таким же знакомым, как и ваше собственное имя.

Как вы, наверное, знаете, дБ означает децибел. Это логарифмическая единица, которая обеспечивает удобный способ работы с отношениями, такими как отношение между амплитудами входного и выходного сигналов.

Отношение напряжений сигналов на выходе и входе усилителя

Мы не будем описывать общую информацию о децибелах, потому что она уже доступна на этой странице учебника «Основы электроники и схемотехники». Вместо этого мы сосредоточимся на практических аспектах децибелов в конкретном контексте радиочастотных систем.

Относительный, не абсолютный

Легко забыть, что дБ является относительной единицей. Вы не можете сказать: «Выходная мощность составляет 10 дБ».

Напряжение является абсолютной величиной, потому что мы всегда говорим о разности потенциалов между двумя точками; обычно мы имеем в виду потенциал одного узла относительно узла земли 0 В. Ток также является абсолютной величиной, поскольку единица измерения (ампер) включает в себя определенное количество заряда в течение определенного количества времени. Децибел, напротив, это единица измерения, которая включает в себя логарифм отношения между двумя числами. Ярким примером является коэффициент усиления усилителя: если мощность входного сигнала равна 1 Вт, а мощность выходного сигнала равна 5 Вт, мы имеем коэффициент 5:

\[10 \log_ <10>\left( < P_<вых>\over P_ <вх>> \right) = 10 \log_ <10>(5) \approx 7 дБ\]

Таким образом, этот усилитель обеспечивает усиление по мощности 7 дБ, то есть соотношение между мощностью выходного сигнала и мощностью входного сигнала может быть выражено как 7 дБ.

Почему дБ?

Конечно, можно было бы проектировать и тестировать радиочастотные системы без использования дБ, но на практике дБ используются везде. Одно из преимуществ заключается в том, что шкала дБ позволяет выражать очень большие отношения без использования очень больших чисел: усиление по мощности в 1 000 000 раз составляет всего 60 дБ. Кроме того, при использовании дБ легко вычисляется общий коэффициент усиления или потерь в цепи прохождения сигнала, поскольку отдельные значения в дБ просто складываются (тогда как, если бы мы работали с обычными отношениями, нам потребовалось бы умножение).

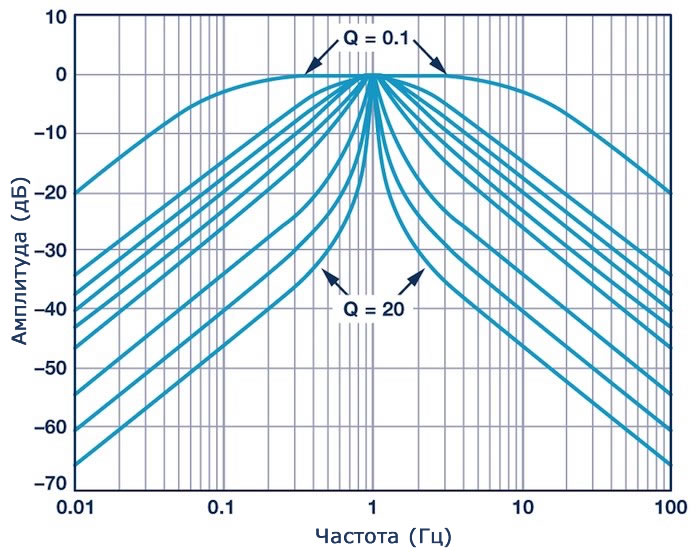
Еще одно преимущество – это то, что мы знаем из нашего опыта работы с фильтрами. Радиочастотные системы вращаются вокруг частот и различных способов генерации, управления или воздействия на эти частоты с помощью компонентов и паразитных элементов схемы. Шкала в дБ в подобном контексте удобна, потому что графики частотных характеристик интуитивно понятны и визуально информативны, когда ось частот использует логарифмический масштаб, а ось амплитуды использует шкалу в дБ.

Диаграмма Боде, показывающая амплитудно-частотные характеристики различных полосовых фильтров

Когда дБ абсолютны?

Мы установили, что дБ является отношением и, следовательно, не может описывать абсолютные значения мощности и амплитуды сигнала. Однако было бы неудобно постоянно переключаться между значениями в дБ и не в дБ, и, возможно, именно поэтому радиоинженеры ввели единицу измерения дБм (dBm).

Мы можем избежать проблемы «только отношение», просто создав новую единицу измерения, которая всегда будет содержать опорное значение. В случае дБм опорное значение равно 1 мВт. Таким образом, если у нас есть сигнал 5 мВт, и мы хотим оставаться в области дБ, мы можем выразить мощность этого сигнала как 7дБм:

\[10 \log_ <10>\left( < 5 мВт \over 1 мВт >\right) = 10 \log_ <10>(5) \approx 7 дБм\]

Вы определенно хотите ознакомиться с концепцией дБм. Это стандартная единица, используемая в реальной разработке радиочастотных систем, и она очень удобна, когда вы, например, вычисляете энергетический баланс линии связи, поскольку усиления и потери, выраженные в дБ, могут просто складываться и вычитаться из выходной мощности, выраженной в дБм.

Существует также единица дБВт (dBW); в качестве опорного значения она использует 1 Вт вместо 1 мВт. В настоящее время большинство радиоинженеров работает с относительно маломощными системами, и это, вероятно, объясняет, почему дБм встречается чаще.

Больше вариаций дБ

Две других единицы измерения, основанных на дБ, – это дБн (dBc) и дБи (dBi).

Вместо фиксированного значения, такого как 1 мВт, дБн (dBc) использует в качестве опорного сигнала уровень несущей сигнала. Например, фазовый шум (смотрите второй раздел данной главы) выражается в единицах дБн/Гц (dBc/Hz); первая часть этой единицы измерения указывает, что мощность фазового шума на определенной частоте измеряется относительно мощности несущей (в этом случае «несущая» относится к мощности сигнала на номинальной частоте).

Идеализированная точечная антенна принимает определенное количество энергии от схемы передатчика и равномерно излучает ее во всех направлениях. Считается, что эти «изотропные» антенны имеют нулевой коэффициент усиления и нулевые потери.

Однако, другие антенны могут быть сконструированы таким образом, чтобы концентрировать излучаемую энергию в определенных направлениях, и в этом смысле антенна может иметь «усиление». Антенна на самом деле не добавляет мощности к сигналу, но эффективно увеличивает переданную мощность путем концентрации электромагнитного излучения в соответствии с направлением системы связи (очевидно, что более практично, когда разработчик антенны знает пространственную взаимосвязь между передатчиком и приемником).

Здесь вы можете увидеть неравномерное распределение излучаемой энергии, которая приводит к усилению в прямом направлении (т.е., 0°)

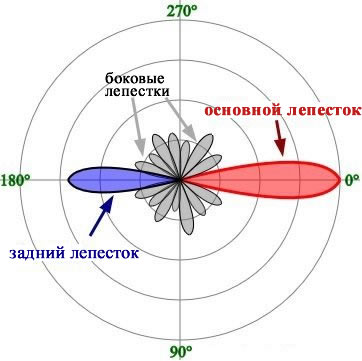
Единица измерения дБи (dBi) позволяет производителям антенн указывать «коэффициент усиления», который использует популярную шкалу дБ. Как всегда, когда мы работаем с дБ, нам необходимо отношение, а в случае с дБи (dBi) коэффициент усиления антенны выражается через опорное усиление изотропной антенны.

Некоторые антенны (например, те, которые сопровождаются параболическим зеркалом, «тарелкой») имеют значительный коэффициент усиления, и поэтому они могут внести нетривиальный вклад в расстояние и производительность радиочастотной системы.

Источник

Что такое децибел?

Перевод из децибел в разы и обратно

Довольно часто в популярной радиотехнической литературе, в описании электронных схем употребляется единица измерения – децибел (дБ или dB).

При изучении электроники начинающий радиолюбитель привык к таким абсолютным единицам измерения как Ампер (сила тока), Вольт (напряжение и ЭДС), Ом (электрическое сопротивление) и многим другим, с помощью которых обозначают количественно тот или иной электрический параметр (ёмкость, индуктивность, частоту).

Начинающему радиолюбителю, как правило, не составляет особого труда разобраться, что такое ампер или вольт. Тут всё понятно, есть электрический параметр или величина, которую нужно измерить. Есть начальный уровень отсчёта, который принимается по умолчанию в формулировке данной единицы измерения. Есть условное обозначение этого параметра или величины (A, V). И вправду, как только мы читаем надпись 12 V, то мы понимаем, что речь идёт о напряжении, аналогичном, например, напряжению автомобильной аккумуляторной батареи.

Но как только встречается надпись, к примеру: напряжение повысилось на 3 дБ или мощность сигнала составляет 10 дБм (10 dBm), то у многих возникает недоумение. Как это? Почему упоминается напряжение или мощность, а значение указывается в каких-то децибелах?

Практика показывает, что не многие начинающие радиолюбители понимают, что же такое децибел. Попытаемся развеять непроглядный туман над такой таинственной единицей измерения как децибел.

Что такое децибел?

Единицу измерения под названием Бел стали впервые применять инженеры телефонной лаборатории Белла. Децибел является десятой частью Бела (1 децибел = 0,1 Бел). На практике широко используется как раз децибел.

Как уже говорилось, децибел, это особенная единица измерения. Стоит отметить, что децибел не является частью официальной системы единиц СИ. Но, несмотря на это, децибел получил признание и занял прочное место наряду с другими единицами измерения.

Вспомните, когда мы хотим объяснить какое-либо изменение, мы говорим, что, например, стало ярче в 2 раза. Или, например, напряжение упало в 10 раз. При этом мы устанавливаем определённый порог отсчёта, относительно которого и произошло изменение в 10 или 2 раза. С помощью децибел также измеряют эти “разы”, только в логарифмическом масштабе.

График логарифмической зависимости

Например, изменение на 1 дБ, соответствует изменению энергетической величины в 1,26 раза. Изменение на 3 дБ соответствует изменению энергетической величины в 2 раза.

Но зачем так заморачиваться с децибелами, если отношения можно измерять в разах? На этот вопрос нет однозначного ответа. Но уж, поскольку, децибелы активно применяются, то наверняка это оправдано.

Причины для использования децибел всё-таки есть. Перечислим их.

Частично ответ на этот вопрос кроется в так называемом законе Вебера-Фехнера. Это эмпирический психофизиологический закон, т.е основан он на результатах реальных, а не теоретических экспериментов. Суть его заключается в том, что любые изменения каких-либо величин (яркости, громкости, веса) ощущаются нами при условии, если эти изменения носят логарифмический характер.

График зависимости ощущения громкости от силы (мощности) звука. Закон Вебера-Фехнера

Так, например, чувствительность человеческого уха уменьшается с ростом уровня громкости звукового сигнала. Именно поэтому, при выборе переменного резистора, который планируется применить в регуляторе громкости звукового усилителя стоит брать с показательной зависимостью сопротивления от угла поворота ручки регулятора. В этом случае, при повороте движка регулятора громкости звук в динамике будет нарастать плавно. Регулировка громкости будет линейной, так как показательная зависимость регулятора громкости компенсирует логарифмическую зависимость нашего слуха и в сумме станет линейной. При взгляде на рисунок это станет более понятно.

Зависимость сопротивления переменного резистора от угла поворота движка (А-линейная, Б-логарифмическая, В-показательная)

Здесь показаны графики зависимости сопротивления переменных резисторов разных типов: А – линейная, Б – логарифмическая, В – показательная. Как правило, на переменных резисторах отечественного производства указывается, какой зависимостью обладает переменный резистор. На тех же принципах основаны цифровые и электронные регуляторы громкости.

Также стоит отметить, что человеческое ухо воспринимает звуки, мощность которых различается на колоссальную величину в 10 000 000 000 000 раз! Таким образом, самый громкий звук отличается от самого тихого, который может уловить наш слух, на 130 дБ (10 000 000 000 000 раз).

Вторая причина широкого использования децибел является простота вычислений.

Согласитесь, что куда проще при вычислениях использовать небольшие числа вроде 10, 20, 60,80,100,130 (наиболее часто используемые числа при расчёте в децибелах) по сравнению с числами 100 (20 дБ), 1000 (30 дБ), 1000 000 (60 дБ),100 000 000 (80 дБ),10 000 000 000 (100 дБ), 10 000 000 000 000 (130 дБ). Ещё одним достоинством децибел является то, что их просто суммируют. Если проводить вычисления в разах, то числа необходимо умножать.

Например, 30 дБ + 30 дБ = 60 дБ (в разах: 1000 * 1000 = 1000 000). Думаю, с этим всё ясно.

Также децибелы очень удобны при графическом построении различных зависимостей. Все графики вроде диаграмм направленности антенн, амплитудно-частотных характеристик усилителей выполняют с применением децибел.

Децибел является безразмерной единицей измерения. Мы уже выяснили, что децибел на самом деле показывает, во сколько раз возросла, либо уменьшилась какая-либо величина (ток, напряжение, мощность). Отличие децибел от разов заключается лишь в том, что происходит измерение по логарифмическому масштабу. Чтобы это как-то обозначить и приписывают обозначение дБ. Так или иначе, при оценке приходится переходить от децибел к разам. Сравнивать с помощью децибел можно любые единицы измерения (не только ток, напряжение и проч.), так как децибел является относительной, безразмерной величиной.

Если указывается знак “-”, например, –1 дБ, то значение измеряемой величины, например, мощности, уменьшилось в 1,26 раз. Если перед децибелами не ставят никакого знака, то речь идёт об увеличении, росте величины. Это стоит учитывать. Иногда вместо знака “-” говорят о затуханиях, снижении коэффициента усиления.

Переход от децибел к разам.

На практике чаще всего приходится переходить от децибел к разам. Для этого есть простая формула:

Внимание! Данные формулы применяются для так называемых “энергетических” величин. Таких как энергия и мощность.

Например, 1дБ равен 10 (1дБ / 10) = 1,258925…= 1,26 раза.

при 20 дБ: 10 (20дБ / 10) = 100 (увеличение величины в 100 раз)

при 10 дБ: 10 (10дБ / 10) = 10 (увеличение в 10 раз)

Переход от разов к децибелам можно осуществить по следующей формуле:

Например, рост мощности в 4 раза будет соответствовать значению в 6,021 дБ.

10 * log₁₀(4) = 6,021 дБ.

Внимание! Для пересчёта отношений таких величин как напряжение и сила тока существуют немного иные формулы:

(Сила тока и напряжение, это так называемые “силовые” величины. Поэтому и формулы отличаются.)

Для перехода к децибелам: n = 20 * log₁₀(m)

Для перехода от децибел к разам: m = 10 (n / 20)

n – значение в децибелах, m – отношение в разах.

Если Вы успешно дошли до этих строк, то считайте, что сделали ещё один весомый шаг в освоении электроники!

Источник