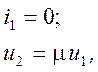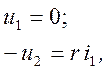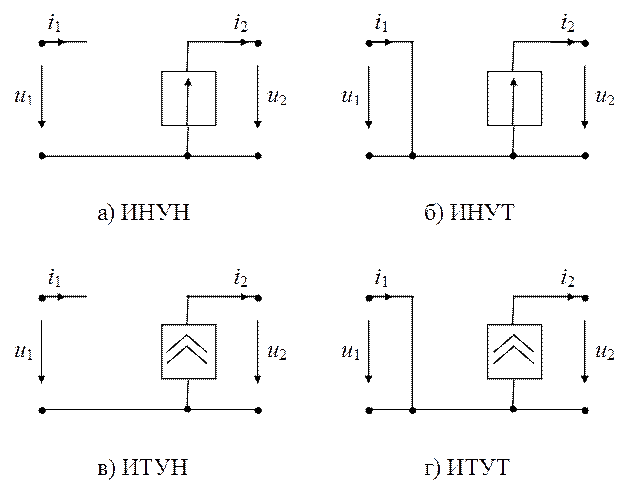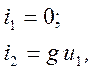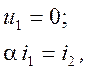Что такое детерминированный сигнал

Детерминированный сигнал

4. Детерминированный сигнал

Сигнал, мгновенные значения которого в любой момент времени известны.

Примечание. Общие характеристики детерминированного сигнала могут быть найдены расчетным путем

Смотреть что такое «Детерминированный сигнал» в других словарях:

детерминированный сигнал — Сигнал, мгновенные значения которого в любой момент времени известны. Примечание Общие характеристики детерминированного сигнала могут быть найдены расчетным путем. [ГОСТ 16465 70] Тематики телевидение, радиовещание, видео Обобщающие термины… … Справочник технического переводчика

Детерминированный сигнал — 1. Сигнал, мгновенные значения которого в любой момент времени известны Употребляется в документе: Приложение № 6 ГОСТ 16465 70 Сигналы радиотехнические измерительные. Термины и определения … Телекоммуникационный словарь

Сигнал (техника) — Сигнал в теории информации и связи называется материальный носитель информации, используемый для передачи сообщений по системе связи. Сигналом может быть любой физический процесс, параметры которого изменяются в соответствии с передаваемым… … Википедия

Сигнал — У этого термина существуют и другие значения, см. Сигнал (значения). Эта статья или раздел нуждается в переработке. Пожалуйста, улучшит … Википедия

Детерминированный автомат — математическая модель системы, состояния которой меняются в дискретные моменты времени, причём каждое состояние системы полностью определяется предыдущим состоянием и входным сигналом. Д. а. формально описывается в виде функции f (si, aj) … Большая советская энциклопедия

импульсный сигнал — импульс Детерминированный сигнал конечной энергии, существенно отличный от нуля в течение ограниченного интервала времени, соизмеримого с временем установления переходного процесса в системе, для воздействия на которую этот сигнал предназначен.… … Справочник технического переводчика

Импульсный сигнал — 5. Импульсный сигнал Импульс Детерминированный сигнал конечной энергии, существенно отличный от нуля в течение ограниченного интервала времени, соизмеримого с временем установления переходного процесса в системе, для воздействия на которую этот… … Словарь-справочник терминов нормативно-технической документации

Импульсный сигнал — 1. Детерминированный сигнал конечной энергии, существенно отличный от нуля в течение ограниченного интервала времени, соизмеримого с временем установления переходного процесса в системе, для воздействия на которую этот сигнал предназначен… … Телекоммуникационный словарь

периодический сигнал — Детерминированный сигнал, мгновенные значения которого повторяются через равные промежутки времени. x(t) = x(t iT), где i любое целое число [ГОСТ 16465 70] Тематики телевидение, радиовещание, видео Обобщающие термины классификация измерительных… … Справочник технического переводчика

Периодический сигнал — 6. Периодический сигнал Детерминированный сигнал, мгновенные значения которого повторяются через равные промежутки времени x(t) = x(t iT), где i любое целое число Источник: ГОСТ 16465 70: Сигналы радиотехнические измерительные. Термины и… … Словарь-справочник терминов нормативно-технической документации

Источник

Детерминированный и Случайный сигналы

Шумом называются нежелательные явления мешающие получать информацию из полезного сигнала. Шум присутствует повсюду, он случаен по своей природе, источниками его может быть как физика самого процесса, который можно зафиксировать, так и неидеальности приемной аппаратуры или оцифровщиков. Нужно различать понятия шумов и полезного сигнала, в том числе и с точки зрения их математического описания.

Детерминированные и случайные сигналы

Давайте рассмотрим, как можно описать полезный сигнал. В качестве математической модели используем детерминированный сигнал заданный аналитической функцией.

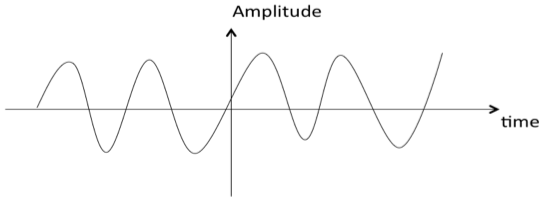
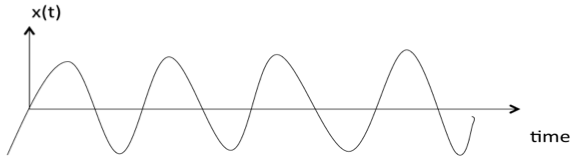
Значение сигнала можно определить в любой момент времени, подставив все необходимые аргументы в описывающую его аналитическую функцию. На примере представлены синусоиды, если зафиксировать параметры амплитуды, частоты и фазы, и передавать в формуле меняющееся значение времени, будем получать точное значение сигнала в эти моменты времени.

Детерминированный сигнал

Детерминированный сигнал описываемой аналитической функции, как модель очень удобен, но сигналы реального мира подвержены воздействию множества физических факторов. Их значения могут колебаться от наблюдения к наблюдению, да и сами средства наблюдения также могут вносить погрешность измерений. Проще говоря, реальный сигнал будет отличаться от его аналитического описания на случайную величину ошибки.

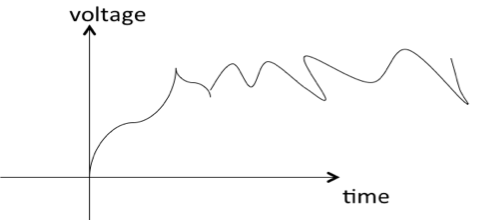
Рассмотрим очередной бытовой пример, нагрев воды в чайнике на газовой горелке. Температура воды с течением времени монотонно нарастает, но мы наблюдаем некоторые флуктуации или отклонения. Это может быть обусловлено неравномерной подачей газа в горелке, ветром, термодинамикой, неидеальностью средств измерения, так или иначе полученные отсчеты мы можем приблизить прямой линией.

Прямая линия это детерминированный сигнал описываемой функции. Можно узнать его значение между соседними отчетами, то есть интерполировать данные эксперименты или даже подсчитать величину сигнала за пределами периода наблюдения, то есть использовать его для прогнозирования значений температуры.

Но реальные значения немного отличаются от линейной зависимости в большую или меньшую сторону. Записанный сигнал можно рассматривать, как математическую модель типа детерминированный сигнал плюс случайный процесс. Если с детерминированным описанием сигналов все более менее понятно, то с моделью случайного процесса нам только предстоит познакомиться.

Случайный процесс

Понятие случайного процесса связано с определением случайной функции. Случайная функция это функция, вид который в результате проведения эксперимента мы не можем предугадать. Случайный процесс — случайная функция времени. Конкретный вид результата протекания случайного процесса называется реализацией. На рисунке ниже показан ансамбль реализации одного случайного процесса.

В отличии от сигналов описываемых аналитической функцией, реализация случайного процесса, практически всегда отличаются друг от друга, но общие характеристики у них есть. Как же нам описать случайный процесс без необходимости хранения бесконечного числа его реализаций? Для описания мы используем теорию вероятностей и математическую статистику.

Распределение случайной величины

Простой пример дискретной случайной величины, число выпадающие при броске игральных костей, может выпасть значение от 1 до 6. Величина может принимать одно из шести дискретных значений, но совершенно случайно. Не трудно подсчитать вероятность выпадения какого-либо числа, она равна 1/6 или 16,67% для каждого из дискретных значений.

Рассмотрим пример непрерывной случайной величины. Рост человека, он не изменяется дискретно, может принимать любое значение в разумных пределах. Представим себе, что мы измеряем рост каждого посетителя, кто заходит в магазин. Измерив достаточное количество людей можно построить вот такой график, по оси x отложен рост в сантиметрах, по оси y количество людей с таким ростом.

На графике мы видим дискретные полоски, но эти полоски обозначают количество людей чей рост попадает в определенной пределы. Например, в пределы от 182 до 183 сантиметров. Взглянув на этот график выше, мы понимаем, что чаще всего в магазин заходили люди среднего роста, а посетителей ростом выше двух метров видели редко. То, что было представлено на графике очень близко к понятию плотности распределения случайной величины.

Плотность распределения

Значение плотности распределения показывает вероятность того, что случайная величина примет определенное значение, а частичная площадь под графиком вероятность того, что значение попадет в выбранный предел.

Как вы понимаете, площадь под графиком на всем диапазоне значений равна единице или 100 %. В случае с игральными костями, мы рассматривали равномерное распределение, то есть одинаковую вероятность того, что случайная величина примет, то или иное значение.

В случае с ростом человека, мы наблюдали нормальное распределение, также именуемое распределением Гаусса. Нормальное распределение широко распространено в природе и используется как удобная модель случайного процесса. Популярность эта вытекает из центральной предельной теоремы, она гласит что сумма большого количества слабо зависимых случайных величин имеет распределение, близкое к нормальному. На отклонение величины от среднего влияет множество факторов, подобно тому, как множество факторов влияет на рост человека, поэтому сумму их влияний можно описать случайным процессом с Гауссовским или Нормальным распределением.

Убедимся в этом в matlab. Смотри с 05:00 минуты!

Плотность распределения это лишь одна из характеристик которыми мы описываем случайные процессы.

Источник

Классификация сигналов

Сигналы подразделяются на следующие категории:

Непрерывное время и сигналы дискретного времени

Детерминированные и недетерминированные сигналы

Четные и нечетные сигналы

Периодические и апериодические сигналы

Сигналы энергии и мощности

Реальные и мнимые сигналы

Непрерывное время и сигналы дискретного времени

Детерминированные и недетерминированные сигналы

Четные и нечетные сигналы

Периодические и апериодические сигналы

Сигналы энергии и мощности

Реальные и мнимые сигналы

Непрерывное время и сигналы дискретного времени

Сигнал называется непрерывным, когда он определен для всех моментов времени.

Сигнал называется дискретным, если он определен только в дискретные моменты времени /

Детерминированные и недетерминированные сигналы

Сигнал называется детерминированным, если нет неопределенности относительно его значения в любой момент времени. Или сигналы, которые могут быть точно определены математической формулой, называются детерминированными сигналами.

Сигнал считается недетерминированным, если в какой-то момент времени существует неопределенность относительно его значения. Недетерминированные сигналы носят случайный характер, поэтому их называют случайными сигналами. Случайные сигналы не могут быть описаны математическим уравнением. Они смоделированы в вероятностных терминах.

Четные и нечетные сигналы

Сигнал называется четным, даже если он удовлетворяет условию x (t) = x (-t)

Пример 1: t2, t4… стоимость и т. Д.

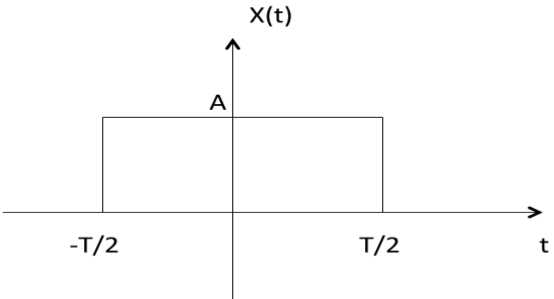
Пример 2: Как показано на следующей диаграмме, функция прямоугольника x (t) = x (-t), поэтому она также является четной функцией.

Источник

Детерминированный сигнал

Употребляется в документе:

Сигналы радиотехнические измерительные. Термины и определения

Смотреть что такое «Детерминированный сигнал» в других словарях:

детерминированный сигнал — Сигнал, мгновенные значения которого в любой момент времени известны. Примечание Общие характеристики детерминированного сигнала могут быть найдены расчетным путем. [ГОСТ 16465 70] Тематики телевидение, радиовещание, видео Обобщающие термины… … Справочник технического переводчика

Детерминированный сигнал — 4. Детерминированный сигнал Сигнал, мгновенные значения которого в любой момент времени известны. Примечание. Общие характеристики детерминированного сигнала могут быть найдены расчетным путем Источник: ГОСТ 16465 70: Сигналы радиотехнические… … Словарь-справочник терминов нормативно-технической документации

Сигнал (техника) — Сигнал в теории информации и связи называется материальный носитель информации, используемый для передачи сообщений по системе связи. Сигналом может быть любой физический процесс, параметры которого изменяются в соответствии с передаваемым… … Википедия

Сигнал — У этого термина существуют и другие значения, см. Сигнал (значения). Эта статья или раздел нуждается в переработке. Пожалуйста, улучшит … Википедия

Детерминированный автомат — математическая модель системы, состояния которой меняются в дискретные моменты времени, причём каждое состояние системы полностью определяется предыдущим состоянием и входным сигналом. Д. а. формально описывается в виде функции f (si, aj) … Большая советская энциклопедия

импульсный сигнал — импульс Детерминированный сигнал конечной энергии, существенно отличный от нуля в течение ограниченного интервала времени, соизмеримого с временем установления переходного процесса в системе, для воздействия на которую этот сигнал предназначен.… … Справочник технического переводчика

Импульсный сигнал — 5. Импульсный сигнал Импульс Детерминированный сигнал конечной энергии, существенно отличный от нуля в течение ограниченного интервала времени, соизмеримого с временем установления переходного процесса в системе, для воздействия на которую этот… … Словарь-справочник терминов нормативно-технической документации

Импульсный сигнал — 1. Детерминированный сигнал конечной энергии, существенно отличный от нуля в течение ограниченного интервала времени, соизмеримого с временем установления переходного процесса в системе, для воздействия на которую этот сигнал предназначен… … Телекоммуникационный словарь

периодический сигнал — Детерминированный сигнал, мгновенные значения которого повторяются через равные промежутки времени. x(t) = x(t iT), где i любое целое число [ГОСТ 16465 70] Тематики телевидение, радиовещание, видео Обобщающие термины классификация измерительных… … Справочник технического переводчика

Периодический сигнал — 6. Периодический сигнал Детерминированный сигнал, мгновенные значения которого повторяются через равные промежутки времени x(t) = x(t iT), где i любое целое число Источник: ГОСТ 16465 70: Сигналы радиотехнические измерительные. Термины и… … Словарь-справочник терминов нормативно-технической документации

Источник

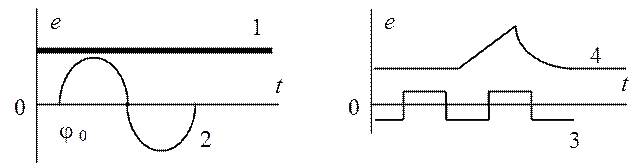
Рассмотрим четыре формы сигналов источников. Постоянный сигнал: e(t) = E = const (рис. 1.9, кривая 1). Гармонический сигнал: e(t) = E_m sin(wt+j₀) (рис. 1.9, кривая 2). Периодический негармонический сигнал, описывается рядом Фурье (рис. 1.9, кривая 3). Непериодический сигнал, описывается интегралом Фурье (рис. 1.9, кривая 4).

Управляемые источники тока и напряжения. Идеальные источники тока и напряжения могут быть и управляемыми (зависимыми). В общем случае управляемый источник — это идеализированный активный элемент с двумя парами выводов, параметр которого является определенной функцией тока или напряжения некоторого участка цепи.

Внутреннее сопротивление управляемого источника напряжения равно нулю, а внутреннее сопротивление управляемого источника тока равно бесконечности.

Источник напряжения, управляемый напряжением (ИНУН), показан на рис. 1.10, а. Уравнения ИНУН:

где m — коэффициент передачи по напряжению.

Источник напряжения, управляемый током (ИНУТ), показан на рис. 1.10, б. Уравнения ИНУТ:

где r — передаточное сопротивление.

Источник тока, управляемый напряжением (ИТУН), показан на рис. 1.10, в. Уравнения ИТУН:

где g — передаточная проводимость.

Источник тока, управляемый током (ИТУТ), представлен на рис. 1.10, г и описывается уравнениями:

где a — коэффициент передачи по напряжению.

Приведенные управляемые источники являются линейно управляемыми, хотя в общем случае зависимости между током и напряжением могут быть произвольной формы. Управляемые источники тока и напряжения широко используют при составлении эквивалентных схем электронных приборов.

1.6. Классификация сигналов

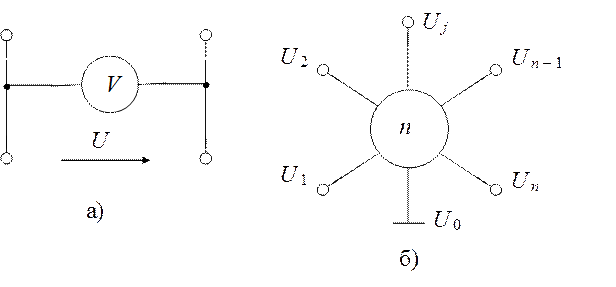
Одномерные и многомерные сигналы. Типичным примером сигнала является напряжение на зажимах (входных или выходных) какой-либо цепи. Такой сигнал описывается одной функцией времени и называется одномерным (например, напряжение u (t) на зажимах вольтметра (рис. 1.11, а).

Многомерный сигнал образуется как множество одномерных 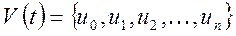, где n — размерность сигнала (рис. 1.11, б).

Детерминированные и случайные сигналы. Детерминированный сигнал — это сигнал, математическая модель которого позволяет предсказать его мгновенное значение в любой момент времени, например:

; ,

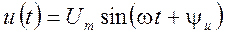
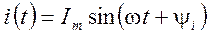
где 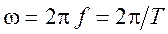— круговая частота, T — период.

Случайный сигнал — это, как правило, помехи, препятствующие получению полезного сигнала из принятого сообщения, вызванные различными флуктуациями (тепловыми, электромагнитными и др.).

В физическом смысле чисто детерминированных сигналов не существует. Любой сигнал содержит в своем составе случайную по времени составляющую (помеху), и часто эти составляющие соизмеримы по величине.

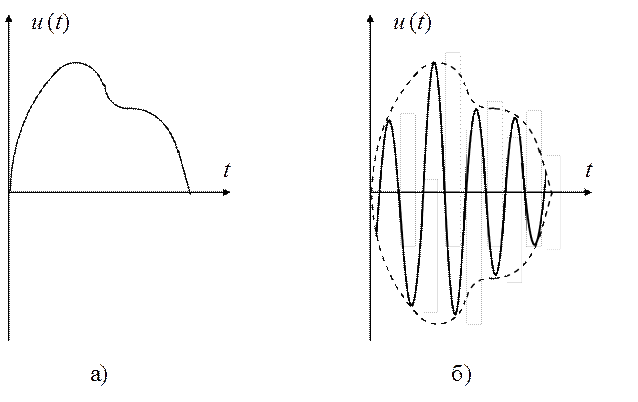
Импульсные сигналы. Импульсные сигналы — это сигналы, существующие лишь в пределах конечных отрезков времени. Они могут следовать во времени с некоторой частотой повторения, либо быть одиночными.

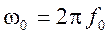
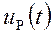
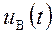
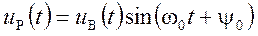
Различают видеоимпульсы (рис. 1.12, а) и радиоимпульсы (рис. 1.12, б). Радиоимпульс представляет собой некоторую несущую частоту , промодулированную видеоимпульсом. Радиоимпульс и видеоимпульс связаны соотношением

.

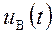
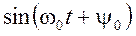
При этом функцию называют огибающей, а функцию — заполнением.

В современной электронике длительность импульсов колеблется от нескольких секунд до долей наносекунды.

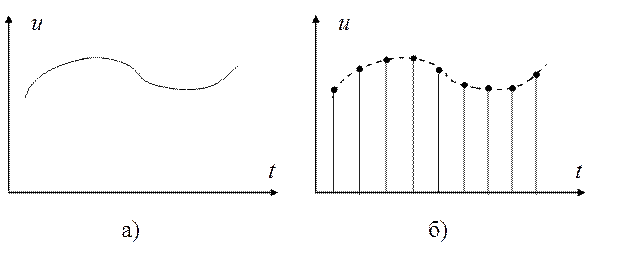
Аналоговые, дискретные и цифровые сигналы. Сигнал, который полностью аналогичен протекающему физическому процессу и который может быть измерен в любой момент времени, называется аналоговым сигналом. Одномерный аналоговый сигнал представляет собой осциллограмму, график которой может быть задан непрерывным (рис. 1.13, а) или дискретным (рис. 1.13, б) способом.

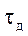
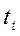
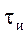
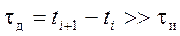
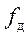
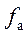
Дискретный сигнал представляет собой счетное множество точек на оси времени, в каждой из которых определено отсчетное значение сигнала . При этом шаг дискретизации — постоянный, постоянна и ширина (длительность) отдельного импульса. Тогда площадь импульса несет информацию о значении сигнала в данной точке. Очевидно, что при этом , а частота дискретного сигнала много больше частоты аналогового сигнала .

Основное достоинство аналогового дискретизированного сигнала состоит в том, что при его воспроизведении достаточно иметь информацию о значениях функции в точках дискретизации и интерполировать остальные значения, что позволяет по одному каналу одновременно передавать большое количество сигналов, используя режим разделения времени.

Однако рассмотренный принцип дискретизации сигнала трудно реализуется физически и сильно зависит от помех при обработке сигнала.

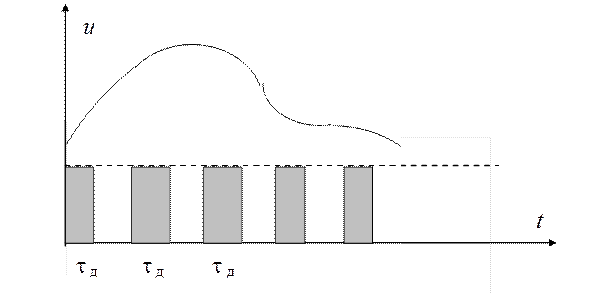
Поскольку информация заключается в площади дискретного импульса, то можно сделать амплитуду импульса постоянной, а длительность поставить в соответствие значению сигнала (рис. 1.14). Это — второй способ дискретизации сигнала.

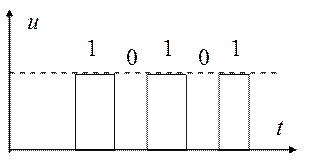
Значение величины сигнала в точках отсчета для обоих способов дискретизации может быть представлено в цифровой форме, например, в двоичной системе счисления. Поскольку цифровая форма записи двоичного числа — это последовательность единиц и нулей, то физическая реализация этой формы выглядит как импульсные сигналы фиксированной частоты и длительности двух уровней, один из которых соответствует единице, а другой — нулю (рис. 1.15).

Для осуществления операции представления аналогового сигнала в цифровой форме и для обратного преобразования соответственно разработаны микросхемы аналого-цифровых (АЦП) и цифро-аналоговых (ЦАП) преобразователей.

1.7. Понятие о компонентных и топологических уравнениях. Закон Ома. Законы Кирхгофа

Математическое описание процессов в электрических цепях базируется на компонентных и топологических уравнениях.

Компонентные уравнения (уравнения компонентов или ветвей) устанавливают связь между током и напряжением каждой ветви в ЭЦ. Количество таких уравнений равно числу ветвей, а вид уравнений зависит от типа рассматриваемого компонента.

Чтобы распечатать файл, скачайте его (в формате Word).

Источник