Что такое десятичная система вычисления
Десятичная система счисления
Система счисления — это способ записи (представление) чисел с помощью определённого набора письменных знаков.
Десятичная система счисления — это позиционная система счисления, в которой для записи чисел используют десять знаков:
1, 2, 3, 4, 5, 6, 7, 8, 9, 0.
Знаки, употребляемые для записи чисел, называются цифрами.
В десятичной системе значение одной и той же цифры зависит от её позиции в записи числа. Для примера возьмём число 777, которое состоит из трёх одинаковых цифр. В этом числе первая слева цифра означает семь сотен, вторая — семь десятков, а третья — семь единиц. Так как значение цифры зависит от её позиции в записи числа, десятичную систему счисления также называют позиционной.
Позиционной называют такую систему счисления, в которой значение цифры зависит от её позиции в записи числа.
Числа, которые записаны с помощью одной цифры, называют однозначными, записанные с помощью двух — двузначными, так же по количеству цифр в числе дают названия и другим числам:
Однозначные числа: 1, 2, 4.
Двузначные числа: 14, 77, 92.
Трёхзначные числа: 122, 345.
Шестизначные числа: 537633, 987345.
Двузначные, трёхзначные, четырёхзначные, пятизначные и т. д. числа называют многозначными.
Следует помнить, что цифра и число не одно и то же.
Цифра – это только письменный знак, используемый для записи числа. Число может быть обозначено не одной, а несколькими цифрами (например, 75) или может быть выражено словами (семьдесят пять).
Системы счисления
Система счисления — это совокупность правил записи чисел посредством конечного набора символов (цифр).
Системы счисления бывают:
Непозиционные системы счисления
Примеры: унарная, римская, древнерусская и др.
Позиционные системы счисления
Основание системы счисления —
количество различных цифр, используемых в этой системе.
отношение количественного эквивалента цифры в этом разряде к количественному эквиваленту той же цифры в нулевом разряде
где i — номер разряда, а s — основание системы счисления.
Разряды числа нумеруются справа налево, причем младший разряд целой части (стоящий перед разделителем — запятой или точкой) имеет номер ноль. Разряды дробной части имеют отрицательные номера:
По определению веса разряда
где i — номер разряда, а s — основание системы счисления.
Тогда, обозначив цифры числа как ai, любое число, записанное в позиционной системе счисления, можем представить в виде:
Например, для системы счисления с основанием 4:
Выполнив вычисления, мы получим значение исходного числа, записанное в десятичной системе счисления (точнее, в той, в которой производим вычисления). В данном случае:
= 1⋅64 + 3⋅16 + 0⋅4 + 2⋅1 + 2⋅0,25 =
= 64 + 48 + 2 + 0,5 = 114,5
Таким образом, для перевода числа из любой системы счисления в десятичную следует:
Вспомним пример перевода из системы счисления с основанием 4 в десятичную:
13024 = 1⋅4 3 + 3⋅4 2 + 0⋅4 1 + 2⋅4 0 = 114
Иначе это можно записать так:
114 = ((1 ⋅ 4 + 3) ⋅ 4 + 0) ⋅ 4 + 2 = 13024
Отсюда видно, что при делении 114 на 4 нацело в остатке должно остаться 2 — это младшая цифра при записи в четверичной системе. Частное же будет равно
Деление его на 4 даст остаток — следующую цифру (0) и частное 1 ⋅ 4 + 3. Продолжая действия, получим аналогичным образом и оставшиеся цифры.
В общем случае для перевода целой части числа из десятичной системы счисления в систему с каким-либо другим основанием необходимо:
Перевод чисел из одной системы счисления в другую
Данный конвертер переводит числа между наиболее популярными системами счисления: десятичной, двоичной, восьмеричной, шестнадцатеричной.
Существуют и другие системы счисления, но мы не стали включать их в конвертер из-за низкой популярности.
Для указания системы счисления при записи числа используется нижний индекс, который ставится после числа:
20010 = 110010002 = 3108 = C816
Кратко об основных системах счисления
Десятичная система счисления. Используется в повседневной жизни и является самой распространенной. Все числа, которые нас окружают представлены в этой системе. В каждом разряде такого числа может использоваться только одна цифра от 0 до 9.
Двоичная система счисления. Используется в вычислительной технике. Для записи числа используются цифры 0 и 1.
Восьмеричная система счисления. Также иногда применяется в цифровой технике. Для записи числа используются цифры от 0 до 7.
Перевод в десятичную систему счисления
Перевод из десятичной системы счисления в другие
Делим десятичное число на основание системы, в которую хотим перевести и записываем остатки от деления. Запишем полученные остатки в обратном порядке и получим искомое число.
Переведем число 37510 в восьмеричную систему:
Перевод из двоичной системы в восьмеричную
Так же как и в первом способе разбиваем число на группы. Но вместо преобразований в скобках просто заменим полученные группы (триады) на соответствующие цифры восьмеричной системы, используя таблицу триад:
Перевод из двоичной системы в шестнадцатеричную
Также как и в первом способе разбиваем число на группы по 4 цифры. Заменим полученные группы (тетрады) на соответствующие цифры шестнадцатеричной системы, используя таблицу тетрад:
| Тетрада | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Цифра | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
Перевод из восьмеричной системы в двоичную
Каждый разряд восьмеричного числа будем делить на 2 и записывать остатки в обратном порядке, формируя группы по 3 разряда двоичного числа. Если в группе получилось меньше 3 разрядов, тогда дополняем нулями. Записываем все группы по порядку, отбрасываем ведущие нули, если имеются, и получаем двоичное число.
Используем таблицу триад:
Каждую цифру исходного восьмеричного числа заменяется на соответствующие триады. Ведущие нули самой первой триады отбрасываются.
Перевод из шестнадцатеричной системы в двоичную
Аналогично переводу из восьмеричной в двоичную, только группы по 4 разряда.
Используем таблицу тетрад:
| Цифра | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Тетрада | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
Каждую цифру исходного числа заменяется на соответствующие тетрады. Ведущие нули самой первой тетрады отбрасываются.
Перевод из восьмеричной системы в шестнадцатеричную и наоборот
Такую конвертацию можно осуществить через промежуточное десятичное или двоичное число. То есть исходное число сначала перевести в десятичное (или двоичное), и затем полученный результат перевести в конечную систему счисления.
Десятичная система счисления

Всего получено оценок: 202.
Всего получено оценок: 202.
Все вычисления в математике выполняются в позиционной десятичной системе счисления. Кратко об особенностях десятичной системы можно прочитать в данной статье.
Что такое десятичная система счисления
В десятичной системе для представления чисел использует десять арабских цифр от 0 до 9, соответственно основанием десятичной системы счисления является число 10.
Историки, изучающие культуру древнего востока, в Индии обнаружили плиту с начертанием числа в позиционной десятичной системе. Возраст найденного артефакта составляет порядка 1,5 тысяч лет. Здесь же в древней Индии впервые используется ноль, как самостоятельная цифра.
Развернутая форма представления десятичного числа
Важным понятием в позиционном подходе представления чисел является понятие разряда. Различают разряды единиц, десятков, сотен, тысяч и так далее. Любое десятичное число можно представить, в так называемом развернутом виде, когда число записывается в виде суммы разрядных слагаемых, представленных в виде произведения значащей цифры разряда и числа десять в степени соответствующего разряда.
Например, десятичное число 46758 в развернутом виде будет выглядеть следующим образом:
46758 = 4 * 10^4 + 6 * 10^3 + 7 * 10^2 + 5 * 10^1 + 8 * 10^0
46758 = 4 * 10000 + 6 * 1000 + 7 * 100 + 5 * 10 + 8 * 1
Прямой перевод числа из десятичной системы
Перевод целого десятичного числа в какую-либо систему счисления выполняется путем поочередного деления самого числового значения, а затем полученных частных на основание системы счисления, в которую производится перевод.
Например, для перевода десятичного числа в двоичную систему выполняют деление на два, в восьмеричную – на восемь, в шестнадцатеричную – на шестнадцать. В принципе, десятичное число можно перевести и в пятеричную и семеричную системы, выполнив деление на пять или семь.
Выполнив первый шаг деления на, например, два, остаток запоминают, а полученное частное снова делят на основание. Эту операцию выполняют до тех пор, пока последнее частное не будет меньше или равно делителю.
Записывать сформированное число в новой системе счисления необходимо начиная с итогового частного и затем друг за другом выписывая остатки от деления от последнего к первому.
Например, прямой перевод числа 27 из десятичной системы в двоичную выполняют так:
27 / 2 = 13 и остаток 1
13 / 2 = 6 и остаток 1
6 / 2 = 3 и остаток 0
3 / 2 = 1 и остаток 1
Таким образом, 27 в двоичном формате это число 11011.
Для перевода чисел в пределах можно пользоваться таблицей соответствия десятичных и двоичных чисел
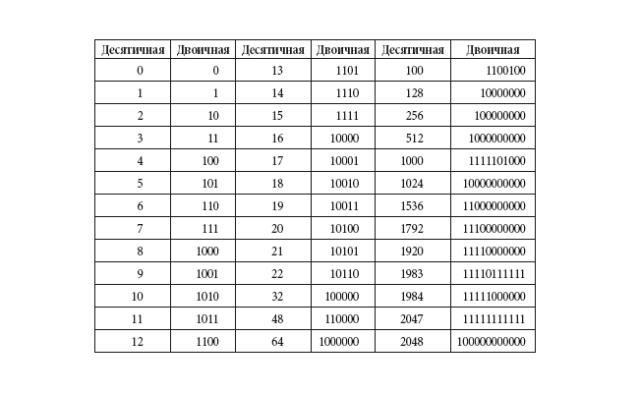
Обратный перевод числа в десятичную систему
Для перевода чисел в десятичную систему удобно пользоваться развернутой формой. При этом числовые значения записываются в виде суммы произведений цифр разрядов на основание текущей системы счисления в степени разряда.
Например, двоичное число 11011 можно представить так:
1 * 2^4 + 1 * 2^3 + 0 * 2^2 + 1 * 2^1 + 1 * 2^0 = 1 * 16 + 1 * 8 + 0 * 4 + 1 * 2 + 1 * 1 =27
Для упрощения вычислений удобно пользоваться таблицей степени двойки
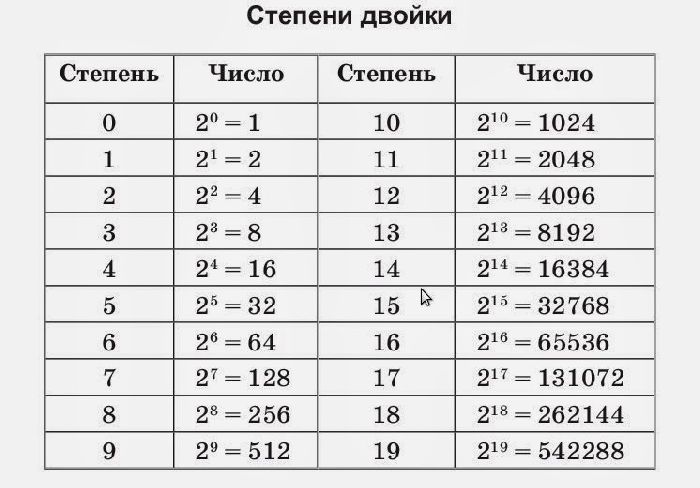
Что мы узнали?
В десятичной позиционной системе для представления числовых значений используются десять арабских цифр. Числа в такой системе можно представлять в развернутом виде. Перевод десятичных чисел в другую систему выполняется путем поочередного деления на основание новой системы счисления. Обратный перевод удобно выполнять с использованием развернутой формы записи числа.
Основные сведения о десятичной системе счисления
Системы счисления. Основные понятия
Система счисления — это набор правил записи чисел посредством конечного набора цифр.
Системы счисления разделяются на:
Основание системы счисления — это количество цифр, используемых в данной системе.
Вес разряда — это отношение количественного эквивалента цифры в данном разряде к количественному эквиваленту такой же цифры в нулевом разряде:
Разряды числа нумеруются справа налево. Младший разряд имеет номер ноль. Разряды дробной части нумеруются отрицательными числами:
Что такое десятичная система счисления
Десятичная система счисления — это система счисления по целочисленному основанию 10 (0,1,2,3,4,5,6,7,8,9 арабские цифры). Она является позиционной системой счисления и наиболее распространенной.
Ученые утверждают, что использование такой распространенной системы связана с количеством пальцев на руках у человека.
Десятичные цифры используют в двоично-десятичном кодировании в двоичных компьютерах.
Алгоритм перевода чисел из любой системы счисления в десятичную
Перевести целое число с основанием q в десятичное можно с помощью следующего алгоритма:
Также можно переводить дроби с основанием q в десятичную систему счисления. Воспользуемся следующей формулой:
Примеры решения задач
Дано число в двоичной система 10011. Перевести число в десятичную систему счисления.
10011 2 = 1 ∙ 2 4 + 0 ∙ 2 3 + 0 ∙ 2 2 + 1 ∙ 2 1 + 1 ∙ 2 0 = 1 ∙ 16 + 0 ∙ 8 + 0 ∙ 4 + 1 ∙ 2 + 1 ∙ 1 = 16 + 0 + 0 + 2 + 1 = 19 10
Перевести в десятичную систему счисления число 17 из восьмеричной системы.
17 8 = 1 ∙ 8 1 + 7 ∙ 8 0 = 1 ∙ 8 + 7 ∙ 1 = 8 + 7 = 15 10
Перевести из пятеричной системы счисления число 20341 в десятичную систему.
20341 5 = 2 ∙ 5 4 + 0 ∙ 5 3 + 3 ∙ 5 2 + 4 ∙ 5 1 + 1 ∙ 5 0 = 2 ∙ 625 + 0 ∙ 125 + 3 ∙ 25 + 4 ∙ 5 + 1 ∙ 1 = 1250 + 0 + 75 + 20 + 1 = 1346 10
Число 0,F3D0 из шестнадцатеричной системы счисления перевести в десятичную систему.
Перевести в десятичную систему счисления двоичное число 101,11.
