Что такое десятичная система счисления 5 класс
Десятичная система счисления
Система счисления — это способ записи (представление) чисел с помощью определённого набора письменных знаков.
Десятичная система счисления — это позиционная система счисления, в которой для записи чисел используют десять знаков:
1, 2, 3, 4, 5, 6, 7, 8, 9, 0.
Знаки, употребляемые для записи чисел, называются цифрами.
В десятичной системе значение одной и той же цифры зависит от её позиции в записи числа. Для примера возьмём число 777, которое состоит из трёх одинаковых цифр. В этом числе первая слева цифра означает семь сотен, вторая — семь десятков, а третья — семь единиц. Так как значение цифры зависит от её позиции в записи числа, десятичную систему счисления также называют позиционной.
Позиционной называют такую систему счисления, в которой значение цифры зависит от её позиции в записи числа.
Числа, которые записаны с помощью одной цифры, называют однозначными, записанные с помощью двух — двузначными, так же по количеству цифр в числе дают названия и другим числам:
Однозначные числа: 1, 2, 4.
Двузначные числа: 14, 77, 92.
Трёхзначные числа: 122, 345.
Шестизначные числа: 537633, 987345.
Двузначные, трёхзначные, четырёхзначные, пятизначные и т. д. числа называют многозначными.
Следует помнить, что цифра и число не одно и то же.
Цифра – это только письменный знак, используемый для записи числа. Число может быть обозначено не одной, а несколькими цифрами (например, 75) или может быть выражено словами (семьдесят пять).
Математика. 5 класс
Конспект урока
Ряд натуральных чисел. Десятичная система записи натуральных чисел
Перечень вопросов, рассматриваемых в теме:
— десятичная запись натуральных чисел;
— разрядность натуральных чисел
Натуральные числа – числа, которые используют при подсчёте предметов.
Натуральный ряд – последовательность всех натуральных чисел, расположенных в порядке возрастания.
Система счисления – это способ записи чисел с помощью заданного набора специальных знаков (цифр).
Теоретический материал для самостоятельного изучения
С древних времен у человека была потребность в счёте.
Числа, которые используют при подсчёте предметов, называют натуральными числами.
Таким образом, числа: один, два, три, …, десять, …, сто, …, тысяча, …, миллион и так далее – это натуральные числа.
Натуральные числа один, два, три, четыре, пять и так далее, записанные в порядке возрастания и без пропусков, образуют ряд натуральных чисел.
Стоит отметить, что самое маленькое натуральное число – единица (1). В натуральном ряду каждое следующее число на 1 больше предыдущего. Натуральный ряд бесконечен, наибольшего числа в нём нет.
В настоящее время принята десятичная система записи чисел (десятичная система счисления), в которой числа записываются при помощи десяти знаков: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 – эти знаки называют цифрами.
Одна и та же цифра может иметь различное значение в зависимости от позиции, где она расположена в записи числа. Например, в записи числа пятьсот пятьдесят пять первая справа цифра пять означает пять единиц, вторая – пять десятков, третья – пять сотен.
Вот поэтому десятичную систему счисления называют позиционной.
Натуральные числа, записанные одной цифрой, называют однозначными, а записанные несколькими цифрами – многозначными: двумя – двузначными, тремя – трёхзначными и т. д.
Например, числа 1, 8, 9 – однозначные числа; 10, 66, 89 – двузначные числа; 111, 145 – трёхзначные числа; 123456 – шестизначное число.
Для чтения многозначных чисел их разбивают, начиная справа, на группы по три цифры в каждой (самая левая группа может состоять из одной или двух цифр). Эти группы называются классами.
Первый класс справа называют классом единиц, второй – классом тысяч, третий – классом миллионов, четвёртый – классом миллиардов и т. д.
Основные сведения о десятичной системе счисления
Системы счисления. Основные понятия
Система счисления — это набор правил записи чисел посредством конечного набора цифр.
Системы счисления разделяются на:
Основание системы счисления — это количество цифр, используемых в данной системе.
Вес разряда — это отношение количественного эквивалента цифры в данном разряде к количественному эквиваленту такой же цифры в нулевом разряде:
Разряды числа нумеруются справа налево. Младший разряд имеет номер ноль. Разряды дробной части нумеруются отрицательными числами:
Что такое десятичная система счисления
Десятичная система счисления — это система счисления по целочисленному основанию 10 (0,1,2,3,4,5,6,7,8,9 арабские цифры). Она является позиционной системой счисления и наиболее распространенной.
Ученые утверждают, что использование такой распространенной системы связана с количеством пальцев на руках у человека.
Десятичные цифры используют в двоично-десятичном кодировании в двоичных компьютерах.
Алгоритм перевода чисел из любой системы счисления в десятичную
Перевести целое число с основанием q в десятичное можно с помощью следующего алгоритма:
Также можно переводить дроби с основанием q в десятичную систему счисления. Воспользуемся следующей формулой:
Примеры решения задач
Дано число в двоичной система 10011. Перевести число в десятичную систему счисления.
10011 2 = 1 ∙ 2 4 + 0 ∙ 2 3 + 0 ∙ 2 2 + 1 ∙ 2 1 + 1 ∙ 2 0 = 1 ∙ 16 + 0 ∙ 8 + 0 ∙ 4 + 1 ∙ 2 + 1 ∙ 1 = 16 + 0 + 0 + 2 + 1 = 19 10
Перевести в десятичную систему счисления число 17 из восьмеричной системы.
17 8 = 1 ∙ 8 1 + 7 ∙ 8 0 = 1 ∙ 8 + 7 ∙ 1 = 8 + 7 = 15 10
Перевести из пятеричной системы счисления число 20341 в десятичную систему.
20341 5 = 2 ∙ 5 4 + 0 ∙ 5 3 + 3 ∙ 5 2 + 4 ∙ 5 1 + 1 ∙ 5 0 = 2 ∙ 625 + 0 ∙ 125 + 3 ∙ 25 + 4 ∙ 5 + 1 ∙ 1 = 1250 + 0 + 75 + 20 + 1 = 1346 10
Число 0,F3D0 из шестнадцатеричной системы счисления перевести в десятичную систему.
Перевести в десятичную систему счисления двоичное число 101,11.
Урок по математике для 5 класса : Десятичная система счисления


1. Организационный этап
Создать благоприятный психологический настрой на работу
Приветствие, проверка подготовленности к учебному занятию, организация внимания детей.
Включаются в деловой ритм урока.
Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками.
Регулятивные: организация своей учебной деятельности
Личностные: мотивация учения
2. Актуализация знаний
Актуализация опорных знаний и способов действий.
Организация устного счета
Участвуют в работе по повторению: в беседе с учителем отвечают на поставленные вопросы.
Познавательные: структурирование собственных знаний.
Коммуникативные: организовывать и планировать учебное сотрудничество с учителем и сверстниками.
Регулятивные: контроль и оценка процесса и результатов деятельности.
Личностные: оценивание усваиваемого материала.
3. Постановка цели и задач урока. Мотивация учебной деятельности учащихся.
Обеспечение мотивации учения детьми, принятие ими целей урока.
Мотивирует учащихся, вместе с ними определяет цель урока; акцентирует внимание учащихся на значимость темы.
определяют тему и цель урока.
Познавательные: умение осознанно и произвольно строить речевое высказывание в устной форме.
Коммуникативные: умение вступать в диалог, участвовать в коллективном обсуждении вопроса.
4. Применение знаний и умений в новой ситуации
Показать разнообразие заданий
Организация и контроль за процессом решения задач.
Работают в парах над поставленными задачами.
Познавательные: формирование интереса к данной теме.
Личностные: формирование готовности к самообразованию.
Коммуникативные: уметь оформлять свои мысли в устной форме; слушать и понимать речь других.
Регулятивные: п ланирование своей деятельности для решения поставленной задачи и контроль полученного результата.
Сменить деятельность, обеспечить эмоциональную разгрузку учащихся.
Учащиеся сменили вид деятельности и готовы продолжить работу.
6. Контроль усвоения, обсуждение допущенных ошибок и их коррекция.
Дать качественную оценку работы класса и отдельных обучаемых.
Выявляет качество и уровень усвоения знаний, а также устанавливает причины выявленных ошибок.
Учащиеся анализируют свою работу, выражают вслух свои затруднения и обсуждают правильность решения задач.
Личностные: формирование пози-тивной самооценки
Регулятивные: умение самостоя-тельно адекватно анализировать правильность выполнения действий и вносить необходимые коррек-тивы.
7. Рефлексия (подведение итогов урока)
Дать количественную оценку работы учащихся
Подводит итоги работы класса в целом.
Учащиеся сдают выданные задания.
Регулятивные: оценивание собственной деятельности на уроке
8. Информация о домашнем задании
Обеспечение понимания детьми содержания и способов выполнения домашнего задания
Дает комментарий к домашнему заданию
Учащиеся записывают в дневники задание .
Технологическая карта урока
Учитель: Очирова Дарима Гармаевна
Тема урока : Десятичная система счисления
Образовательная: познакомиться с системами счисления; сформировать умения работать с римскими числами и раскладывать числа на разрядные единицы.
Развивающая: развить логическое мышление, память, внимание, навыки самостоятельной работы, математической речи, контроля и самоконтроля.
Воспитательная: воспитать интерес к предмету, точность и аккуратность в оформлении заданий.
Тип урока : изучение нового материала
Формы организации учебной деятельности : индивидуальная, групповая, коллективная.
Оборудование: доска, проектор, презентация, задания для выполнения на уроке,
Характеристика учебных возможностей и предшествующих достижений учащихся класса, для которого проектируется урок:
Создать благоприятный психологический настрой на работу
Учитель приветствует учащихся, проверяет их готовность к уроку, организация внимания детей.
Включаются в деловой ритм урока.
Коммуникативные: планирование учеб-ного сотрудничества с учителем и сверст-никами.
Регулятивные: организация своей учеб-ной деятельности
Личностные: мотивация учения
2. Актуализация зна
Актуализация опорных знаний и способов действий.
Организация устного счета.
1. «Математическая разминка».
5 5 5 5 = 30 (Ответ: 5 + 5 * 5 + 5 = 30)
5 5 5 5 = 55 (Ответ: 5 * (5 + 5) + 5 = 55)
5 5 5 5 = 120 (Ответ: 5 * 5 * 5 – 5 = 120).
2. Сколько ушей у двух мышей?(4) Сколько лап у двух медвежат? (8)Три лошади в упряжке пробежали 90 км. Сколько км пробежала каждая лошадь?
3. Класс делится на две команды. К доске приглашается с рабочей тетрадью по 1 человеку от каждой команды. Кому присвоить звание «Лучший счетчик»? Нужно устно сосчитать и записать на доске только ответ. Рабочая тетрадь. Ч.1, стр. 12 № 22.
— устно выполняют предложенные задания.
(идет соревнования между колонками.)
— Ставят знаки действий.
— Работают устно по цепочке
— Записывают результат на доске
Познавательные: структурирование собственных знаний.
Коммуникативные: организовывать и планировать учебное сотрудничество с учителем и сверстниками.
Регулятивные: контроль и оценка процесса и результатов деятельности.
Личностные: оценивание усваиваемого материала.
3.Постановка цели и задач урока. Мотивация учебной деятельности учащихся.
Обеспечение мотивации учения детьми, принятие ими целей урока.
— учитель задает серию вопросов, необходимых для:
1) формулирования цели урока;
2) прогнозирования содержания нового способа действий.
На доске записано высказывание: «Числа правят миром»
— Что можете сказать об этом высказывании?
( В начальной школе вы познакомились с записью чисел с помощью цифр: 1,2,3,4,5,6,7,8,9,0.)
— учитель предлагает вспомнить историю чисел с древних времен…
— Сформулируйте тему урока ( Десятичная система счисления ).
— Запишите тему в тетрадь.
Тема урока: Десятичная система счисления
– Чему мы должны научиться на уроке?
Уметь записывать, пользуясь римской нумерацией, числа; работать с тестовыми заданиями; приводить и разбирать примеры
Формирование умения заполнять и оформлять таблицы, отвечать на вопросы с помощью таблицы. Анализирование полученных результатов
Познакомиться с системами счисления.
Сформировать умение работать с римскими числами и раскладывать числа на разрядные единицы.
— Как вы думаете, где используют римскую нумерацию? (Сейчас римской нумерацией пользуются для обозначения
юбилейных дат, нумерации некоторых страниц книги (например, страниц предисловия), глав в книгах, строф в стихотворениях и т.д.)
— Записывают дату в тетрадь, определяют тему и цель урока.
— Слушают объяснение учителя
-Выстраивают монологический рассказ в соответствии с поставленными вопросами; формулируют тему и цели урока.
— Отвечают на вопросы
Познавательные: умение осознанно и произвольно строить речевое высказывание в устной форме.
4.Применение знаний и умений в новой ситуации
Показать разнообразие заданий
— Давайте подумаем, как можно запомнить римские цифры?
— Каким правилом нужно следовать, чтобы прочесть римскую цифру или написать ее?
(Для того, чтобы прочесть римскую цифру или написать ее, нужно следовать основным правилам:
не ставить больше трех одинаковых цифр подряд
все цифры складывать
если младшая цифра ( только одна !) стоит слева ( перед ) от старшей, её нужно вычесть из суммы)
— Подумайте, как записать римскими цифрами число 4? ( IV =5 – 1 = 4)
— Используя правило, запишите римскими цифрами числа 9, 14, 19. ( три ученика выполняют задания у доски, остальные в тетради ) (проверка с помощью учебника на стр. 6)
— р.т. (с.12) №19, 20 ( работа в парах )
— (Индивидуальная работа) Запишите в тетрадь ответы на вопросы римскими числами:
Сколько желаний исполняет золотая рыбка? ( III)
Сколько разбойников было с Али-бабой? ( XL)
Сколько раз надо измерить, прежде чем отрезать? (VII)
— Чем отличаются записи чисел правого и левого столбцов ( задания №1 учебника) кроме того, что в левом столбце они сделаны арабскими цифрами, а в правом – римскими? ( в левом столбце в записи каждого числа используется только одна цифра, а в правом – от 3 до 6 разных цифр )
— Как можно назвать данную запись числа в таком виде? (сумма разрядных слагаемых)
— работа с учебником стр. 7 №2, р.т. (стр.5 №2)
— Подумайте, как можно записать число в виде суммы разрядных слагаемых двумя способами?
— Работа с учебником № 15
Работают в парах над поставленными задачами.
При ответе проговаривается правило.
-три ученика выполняют задания у доски, остальные в тетради
-учащиеся выполняют задания, затем вместе с учителем проверяют верность выполненного задания
— Учащиеся участвуют в беседе.
-учащиеся выполняют задание, затем меняются тетрадями с соседом по парте и оценивают друг друга.
Познавательные: формирование интереса к данной теме.
Личностные: формирование готовности к самообразованию.
Коммуникативные: уметь оформлять свои мысли в устной форме; слушать и понимать речь других; взаимодействие учащихся в парной работе.
Регулятивные: п ланирование своей деятельности для решения поставленной задачи и контроль полученного результата.
Сменить деятельность, обеспечить эмоциональную разгрузку учащихся.
Сменить деятельность, обеспечить эмоциональную разгрузку учащихся.
— Давайте немного отдохнем.
Раз, два, три, четыре, пять (шаги на месте)
Все умеем мы считать (хлопки в ладоши)
Отдыхать умеем тоже (прыжки на месте)
Руки за спину положим (руки за спину)
Голову поднимем выше (поднять голову выше)
И легко-легко подышим (глубокий вдох-выдох)
Подтянитесь на носочках столько раз,
Ровно столько, сколько пальцев
(Показали, сколько пальцев на руках)
На руке у вас (Поднимаемся на носочках 10 раз).
Учащиеся поднимаются с мест, повторяют действия за учителем.
Учащиеся сменили вид деятельности и готовы продолжить работу.
Умение самостоятельно применять свои знания в стандартной, но новой ситуации,
Самостоятельная работа с проверкой на уроке.
1. Запишите число, используя арабскую нумерацию:
а) MMCCCXLII б) MMMCCLXX
2. Запишите число цифрами:
Б) 408 миллионов 256 тысяч;
В) 29 триллионов 78 миллионов
1. Запишите число, используя арабскую нумерацию:
а) MMCCXVIII б) MMDLXXX
2. Запишите число цифрами:
Б) 205 миллионов 37 тысяч;
В) 37 триллионов 45 миллиардов
3. Для числа 36 738 513 807 263 3. Для числа 85 758 364 350 508
а) старший разряд; а) старший разряд;
б) цифру разряда десятков б) цифру разряда десятков
в) разряды, в которых стоит в) разряды, в которых стоит
4. Найдите значение выражения: 4. Найдите значение выражения
А) 8+48:4; б) 14*3-11 А) 12*4+7; б) 77:7-5
Учащиеся выполняют самостоятельную работу по карточкам.
Осуществляют взаимопроверку самостоятельной работы.
Учащиеся сдают самостоятельную работу учителю.
Личностные: формирование позитивной самооценки
Регулятивные: умение самостоятельно адекватно анализировать правильность выполнения действий и вносить необходимые коррективы.
7. Рефлексия (подведение итогов урока)
Оценка (выделе-ние и осознание учащимися того, что уже усвоено и что ещё подлежит усвоению, осознание качества и уровня усвоения);
— Подводим итог урока. Система счисления – удобная, быстрая, помогает, считает, записывает.
“ Счёт и вычисления – основа порядка в голове” (И. Песталоцци)
1. Предлагает продолжить предложение
2. Выставляет оценки
Учащиеся отвечают на вопросы
Регулятивные: оценивание собственной деятельности на уроке
Познавательные: рефлексия способов и условий действия, адекватное понимание причин успеха и неудач, контроль и оценка процесса и результатов деятельности
Коммукативные: умение выражать свои мысли, аргументация
8. Информация о домашнем задании
Обеспечение понимания детьми цели, содержания и способов выполнения дом.задания
Дать комментарий к домашнему заданию
Прочитать теоретический материал учебника стр. 6-7 §1
№ 5, № 13, № 12 – по желанию.
Подготовить устный рассказ «Для чего человеку нужны римские числа»
Учащиеся записывают в дневники задание .
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Ищем педагогов в команду «Инфоурок»
Номер материала: ДA-046263
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Рособрнадзор разрешил провести ВПР по некоторым предметам на компьютерах
Время чтения: 0 минут
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
В России утвердили новый порядок формирования федерального перечня учебников
Время чтения: 1 минута
В Липецкой области начинающие педагоги получат 120 тысяч рублей
Время чтения: 0 минут
Итоговое сочинение успешно написали более 97% выпускников школ
Время чтения: 2 минуты
В Минпросвещения рассказали о формате обучения школьников после праздников
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Десятичная система счисления

Всего получено оценок: 202.
Всего получено оценок: 202.
Все вычисления в математике выполняются в позиционной десятичной системе счисления. Кратко об особенностях десятичной системы можно прочитать в данной статье.
Что такое десятичная система счисления
В десятичной системе для представления чисел использует десять арабских цифр от 0 до 9, соответственно основанием десятичной системы счисления является число 10.
Историки, изучающие культуру древнего востока, в Индии обнаружили плиту с начертанием числа в позиционной десятичной системе. Возраст найденного артефакта составляет порядка 1,5 тысяч лет. Здесь же в древней Индии впервые используется ноль, как самостоятельная цифра.
Развернутая форма представления десятичного числа
Важным понятием в позиционном подходе представления чисел является понятие разряда. Различают разряды единиц, десятков, сотен, тысяч и так далее. Любое десятичное число можно представить, в так называемом развернутом виде, когда число записывается в виде суммы разрядных слагаемых, представленных в виде произведения значащей цифры разряда и числа десять в степени соответствующего разряда.
Например, десятичное число 46758 в развернутом виде будет выглядеть следующим образом:
46758 = 4 * 10^4 + 6 * 10^3 + 7 * 10^2 + 5 * 10^1 + 8 * 10^0
46758 = 4 * 10000 + 6 * 1000 + 7 * 100 + 5 * 10 + 8 * 1
Прямой перевод числа из десятичной системы
Перевод целого десятичного числа в какую-либо систему счисления выполняется путем поочередного деления самого числового значения, а затем полученных частных на основание системы счисления, в которую производится перевод.
Например, для перевода десятичного числа в двоичную систему выполняют деление на два, в восьмеричную – на восемь, в шестнадцатеричную – на шестнадцать. В принципе, десятичное число можно перевести и в пятеричную и семеричную системы, выполнив деление на пять или семь.
Выполнив первый шаг деления на, например, два, остаток запоминают, а полученное частное снова делят на основание. Эту операцию выполняют до тех пор, пока последнее частное не будет меньше или равно делителю.
Записывать сформированное число в новой системе счисления необходимо начиная с итогового частного и затем друг за другом выписывая остатки от деления от последнего к первому.
Например, прямой перевод числа 27 из десятичной системы в двоичную выполняют так:
27 / 2 = 13 и остаток 1
13 / 2 = 6 и остаток 1
6 / 2 = 3 и остаток 0
3 / 2 = 1 и остаток 1
Таким образом, 27 в двоичном формате это число 11011.
Для перевода чисел в пределах можно пользоваться таблицей соответствия десятичных и двоичных чисел
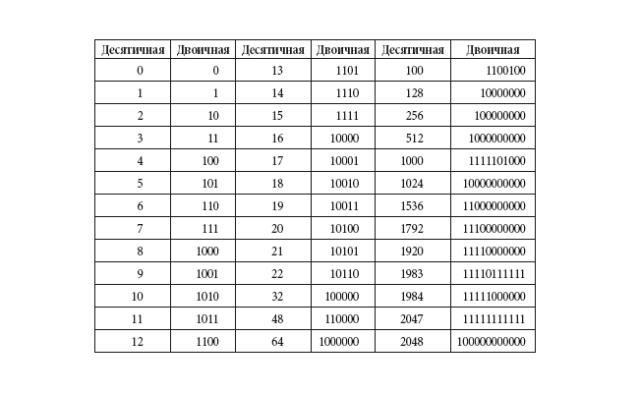
Обратный перевод числа в десятичную систему
Для перевода чисел в десятичную систему удобно пользоваться развернутой формой. При этом числовые значения записываются в виде суммы произведений цифр разрядов на основание текущей системы счисления в степени разряда.
Например, двоичное число 11011 можно представить так:
1 * 2^4 + 1 * 2^3 + 0 * 2^2 + 1 * 2^1 + 1 * 2^0 = 1 * 16 + 1 * 8 + 0 * 4 + 1 * 2 + 1 * 1 =27
Для упрощения вычислений удобно пользоваться таблицей степени двойки
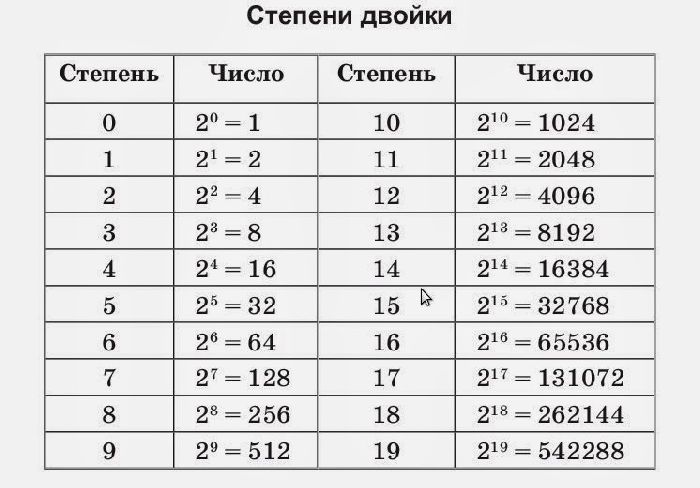
Что мы узнали?
В десятичной позиционной системе для представления числовых значений используются десять арабских цифр. Числа в такой системе можно представлять в развернутом виде. Перевод десятичных чисел в другую систему выполняется путем поочередного деления на основание новой системы счисления. Обратный перевод удобно выполнять с использованием развернутой формы записи числа.







