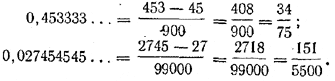Что такое десятичная форма

Основы систем счисления

Изучая кодировки, я понял, что недостаточно хорошо понимаю системы счислений. Тем не менее, часто использовал 2-, 8-, 10-, 16-ю системы, переводил одну в другую, но делалось все на “автомате”. Прочитав множество публикаций, я был удивлен отсутствием единой, написанной простым языком, статьи по столь базовому материалу. Именно поэтому решил написать свою, в которой постарался доступно и по порядку изложить основы систем счисления.

Введение

Система счисления — это способ записи (представления) чисел.

Что под этим подразумевается? Например, вы видите перед собой несколько деревьев. Ваша задача — их посчитать. Для этого можно — загибать пальцы, делать зарубки на камне (одно дерево — один палец\зарубка) или сопоставить 10 деревьям какой-нибудь предмет, например, камень, а единичному экземпляру — палочку и выкладывать их на землю по мере подсчета. В первом случае число представляется, как строка из загнутых пальцев или зарубок, во втором — композиция камней и палочек, где слева — камни, а справа — палочки

Системы счисления подразделяются на позиционные и непозиционные, а позиционные, в свою очередь, — на однородные и смешанные.

Непозиционная — самая древняя, в ней каждая цифра числа имеет величину, не зависящую от её позиции (разряда). То есть, если у вас 5 черточек — то число тоже равно 5, поскольку каждой черточке, независимо от её места в строке, соответствует всего 1 один предмет.

Позиционная система — значение каждой цифры зависит от её позиции (разряда) в числе. Например, привычная для нас 10-я система счисления — позиционная. Рассмотрим число 453. Цифра 4 обозначает количество сотен и соответствует числу 400, 5 — кол-во десяток и аналогично значению 50, а 3 — единиц и значению 3. Как видим — чем больше разряд — тем значение выше. Итоговое число можно представить, как сумму 400+50+3=453.

Однородная система — для всех разрядов (позиций) числа набор допустимых символов (цифр) одинаков. В качестве примера возьмем упоминавшуюся ранее 10-ю систему. При записи числа в однородной 10-й системе вы можете использовать в каждом разряде исключительно одну цифру от 0 до 9, таким образом, допускается число 450 (1-й разряд — 0, 2-й — 5, 3-й — 4), а 4F5 — нет, поскольку символ F не входит в набор цифр от 0 до 9.

Смешанная система — в каждом разряде (позиции) числа набор допустимых символов (цифр) может отличаться от наборов других разрядов. Яркий пример — система измерения времени. В разряде секунд и минут возможно 60 различных символов (от «00» до «59»), в разряде часов – 24 разных символа (от «00» до «23»), в разряде суток – 365 и т. д.

Непозиционные системы

Как только люди научились считать — возникла потребность записи чисел. В начале все было просто — зарубка или черточка на какой-нибудь поверхности соответствовала одному предмету, например, одному фрукту. Так появилась первая система счисления — единичная.

Единичная система счисления

Число в этой системе счисления представляет собой строку из черточек (палочек), количество которых равно значению данного числа. Таким образом, урожай из 100 фиников будет равен числу, состоящему из 100 черточек.
Но эта система обладает явными неудобствами — чем больше число — тем длиннее строка из палочек. Помимо этого, можно легко ошибиться при записи числа, добавив случайно лишнюю палочку или, наоборот, не дописав.

Для удобства, люди стали группировать палочки по 3, 5, 10 штук. При этом, каждой группе соответствовал определенный знак или предмет. Изначально для подсчета использовались пальцы рук, поэтому первые знаки появились для групп из 5 и 10 штук (единиц). Все это позволило создать более удобные системы записи чисел.

Древнеегипетская десятичная система

Почему она называется десятичной? Как писалось выше — люди стали группировать символы. В Египте — выбрали группировку по 10, оставив без изменений цифру “1”. В данном случае, число 10 называется основанием десятичной системы счисления, а каждый символ — представление числа 10 в какой-то степени.

Числа в древнеегипетской системе счисления записывались, как комбинация этих
символов, каждый из которых повторялся не более девяти раз. Итоговое значение равнялось сумме элементов числа. Стоит отметить, что такой способ получения значения свойственен каждой непозиционной системе счисления. Примером может служить число 345:

Вавилонская шестидесятеричная система

В отличии от египетской, в вавилонской системе использовалось всего 2 символа: “прямой” клин — для обозначения единиц и “лежачий” — для десятков. Чтобы определить значение числа необходимо изображение числа разбить на разряды справа налево. Новый разряд начинается с появления прямого клина после лежачего. В качестве примера возьмем число 32:

Число 60 и все его степени так же обозначаются прямым клином, что и “1”. Поэтому вавилонская система счисления получила название шестидесятеричной.
Все числа от 1 до 59 вавилоняне записывали в десятичной непозиционной системе, а большие значения — в позиционной с основанием 60. Число 92:

Запись числа была неоднозначной, поскольку не существовало цифры обозначающей ноль. Представление числа 92 могло обозначать не только 92=60+32, но и, например, 3632=3600+32. Для определения абсолютного значения числа был введен специальный символ для обозначения пропущенного шестидесятеричного разряда, что соответствует появлению цифры 0 в записи десятичного числа:

Теперь число 3632 следует записывать, как:

Шестидесятеричная вавилонская система — первая система счисления, частично основанная на позиционном принципе. Данная система счисления используется и сегодня, например, при определении времени — час состоит из 60 минут, а минута из 60 секунд.

Римская система

Римская система не сильно отличается от египетской. В ней для обозначения чисел 1, 5, 10, 50, 100, 500 и 1000 используются заглавные латинские буквы I, V, X, L, C, D и M соответственно. Число в римской системе счисления — это набор стоящих подряд цифр.

Позиционные системы счисления

Как упоминалось выше — первые предпосылки к появлению позиционной системы возникли в древнем Вавилоне. В Индии система приняла форму позиционной десятичной нумерации с применением нуля, а у индусов эту систему чисел заимствовали арабы, от которых её переняли европейцы. По каким-то причинам, в Европе за этой системой закрепилось название “арабская”.

Десятичная система счисления

Это одна из самых распространенных систем счисления. Именно её мы используем, когда называем цену товара и произносим номер автобуса. В каждом разряде (позиции) может использоваться только одна цифра из диапазона от 0 до 9. Основанием системы является число 10.

Для примера возьмем число 503. Если бы это число было записано в непозиционной системе, то его значение равнялось 5+0+3 = 8. Но у нас — позиционная система и значит каждую цифру числа необходимо умножить на основание системы, в данном случае число “10”, возведенное в степень, равную номеру разряда. Получается, значение равно 5*10 2 + 0*10 1 + 3*10 0 = 500+0+3 = 503. Чтобы избежать путаницы при одновременной работе с несколькими системами счисления основание указывается в качестве нижнего индекса. Таким образом, 503 = 503₁₀.

Помимо десятичной системы, отдельного внимания заслуживают 2-, 8-, 16-ая системы.

Двоичная система счисления

Эта система, в основном, используется в вычислительной технике. Почему не стали использовать привычную нам 10-ю? Первую вычислительную машину создал Блез Паскаль, использовавший в ней десятичную систему, которая оказалась неудобной в современных электронных машинах, поскольку требовалось производство устройств, способных работать в 10 состояниях, что увеличивало их цену и итоговые размеры машины. Этих недостатков лишены элементы, работающие в 2-ой системе. Тем не менее, рассматриваемая система была создана за долго до изобретения вычислительных машин и уходит “корнями” в цивилизацию Инков, где использовались кипу — сложные верёвочные сплетения и узелки.

Двоичная позиционная система счисления имеет основание 2 и использует для записи числа 2 символа (цифры): 0 и 1. В каждом разряде допустима только одна цифра — либо 0, либо 1.

Примером может служить число 101. Оно аналогично числу 5 в десятичной системе счисления. Для того, чтобы перевести из 2-й в 10-ю необходимо умножить каждую цифру двоичного числа на основание “2”, возведенное в степень, равную разряду. Таким образом, число 101₂ = 1*2 2 + 0*2 1 + 1*2 0 = 4+0+1 = 5₁₀.

Хорошо, для машин 2-я система счисления удобнее, но мы ведь часто видим, используем на компьютере числа в 10-й системе. Как же тогда машина определяет какую цифру вводит пользователь? Как переводит число из одной системы в другую, ведь в её распоряжении всего 2 символа — 0 и 1?

Чтобы компьютер мог работать с двоичными числами (кодами), необходимо чтобы они где-то хранились. Для хранения каждой отдельной цифры применяется триггер, представляющий собой электронную схему. Он может находится в 2-х состояниях, одно из которых соответствует нулю, другое — единице. Для запоминания отдельного числа используется регистр — группа триггеров, число которых соответствует количеству разрядов в двоичном числе. А совокупность регистров — это оперативная память. Число, содержащееся в регистре — машинное слово. Арифметические и логические операции со словами осуществляет арифметико-логическое устройство (АЛУ). Для упрощения доступа к регистрам их нумеруют. Номер называется адресом регистра. Например, если необходимо сложить 2 числа — достаточно указать номера ячеек (регистров), в которых они находятся, а не сами числа. Адреса записываются в 8- и 16-ричной системах (о них будет рассказано ниже), поскольку переход от них к двоичной системе и обратно осуществляется достаточно просто. Для перевода из 2-й в 8-ю число необходимо разбить на группы по 3 разряда справа налево, а для перехода к 16-ой — по 4. Если в крайней левой группе цифр не достает разрядов, то они заполняются слева нулями, которые называются ведущими. В качестве примера возьмем число 101100₂. В восьмеричной — это 101 100 = 54₈, а в шестнадцатеричной — 0010 1100 = 2С₁₆. Отлично, но почему на экране мы видим десятичные числа и буквы? При нажатии на клавишу в компьютер передаётся определённая последовательность электрических импульсов, причём каждому символу соответствует своя последовательность электрических импульсов (нулей и единиц). Программа драйвер клавиатуры и экрана обращается к кодовой таблице символов (например, Unicode, позволяющая закодировать 65536 символов), определяет какому символу соответствует полученный код и отображает его на экране. Таким образом, тексты и числа хранятся в памяти компьютера в двоичном коде, а программным способом преобразуются в изображения на экране.

Восьмеричная система счисления

8-я система счисления, как и двоичная, часто применяется в цифровой технике. Имеет основание 8 и использует для записи числа цифры от 0 до 7.

Шестнадцатеричная система счисления

Шестнадцатеричная система широко используется в современных компьютерах, например при помощи неё указывается цвет: #FFFFFF — белый цвет. Рассматриваемая система имеет основание 16 и использует для записи числа: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B. C, D, E, F, где буквы равны 10, 11, 12, 13, 14, 15 соответственно.

Помимо рассмотренных позиционных систем счисления, существуют и другие, например:
1) Троичная
2) Четверичная
3) Двенадцатеричная

Позиционные системы подразделяются на однородные и смешанные.

Однородные позиционные системы счисления

Определение, данное в начале статьи, достаточно полно описывает однородные системы, поэтому уточнение — излишне.

Смешанные системы счисления

К уже приведенному определению можно добавить теорему: “если P=Q n (P,Q,n – целые положительные числа, при этом P и Q — основания), то запись любого числа в смешанной (P-Q)-ой системе счисления тождественно совпадает с записью этого же числа в системе счисления с основанием Q.”

Смешанными системами счисления также являются, например:
1) Факториальная
2) Фибоначчиева

Перевод из одной системы счисления в другую

Иногда требуется преобразовать число из одной системы счисления в другую, поэтому рассмотрим способы перевода между различными системами.

Преобразование в десятичную систему счисления

Пример: 101₂ = 1*2 2 + 0*2 1 + 1*2 0 = 4+0+1 = 5₁₀

Преобразование из десятичной системы счисления в другие

Записав все остатки снизу вверх, получаем итоговое число 17. Следовательно, 15₁₀ = 17₈.

Преобразование из двоичной в восьмеричную и шестнадцатеричную системы

В качестве примера возьмем число 1001₂: 1001₂ = 001 001 = (0*2 2 + 0*2 1 + 1*2 0 ) (0*2 2 + 0*2 1 + 1*2 0 ) = (0+0+1) (0+0+1) = 11₈

Для перевода в шестнадцатеричную — разбиваем двоичное число на группы по 4 цифры справа налево, затем — аналогично преобразованию из 2-й в 8-ю.

Преобразование из восьмеричной и шестнадцатеричной систем в двоичную

Перевод из восьмеричной в двоичную — преобразуем каждый разряд восьмеричного числа в двоичное 3-х разрядное число делением на 2 (более подробно о делении см. выше пункт “Преобразование из десятичной системы счисления в другие”), недостающие крайние разряды заполним ведущими нулями.

Для примера рассмотрим число 45₈: 45 = (100) (101) = 100101₂

Перевод из 16-ой в 2-ю — преобразуем каждый разряд шестнадцатеричного числа в двоичное 4-х разрядное число делением на 2, недостающие крайние разряды заполняем ведущими нулями.

Преобразование дробной части любой системы счисления в десятичную

Преобразование осуществляется также, как и для целых частей, за исключением того, что цифры числа умножаются на основание в степени “-n”, где n начинается от 1.

Преобразование дробной части двоичной системы в 8- и 16-ую

Перевод дробной части осуществляется также, как и для целых частей числа, за тем лишь исключением, что разбивка на группы по 3 и 4 цифры идёт вправо от десятичной запятой, недостающие разряды дополняются нулями справа.

Пример: 1001,01₂ = 001 001, 010 = (0*2 2 + 0*2 1 + 1*2 0 ) (0*2 2 + 0*2 1 + 1*2 0 ), (0*2 2 + 1*2 1 + 0*2 0 ) = (0+0+1) (0+0+1), (0+2+0) = 11,2₈

Преобразование дробной части десятичной системы в любую другую

Для перевода дробной части числа в другие системы счисления нужно обратить целую часть в ноль и начать умножение получившегося числа на основание системы, в которую нужно перевести. Если в результате умножения будут снова появляться целые части, их нужно повторно обращать в ноль, предварительно запомнив (записав) значение получившейся целой части. Операция заканчивается, когда дробная часть полностью обратится в нуль.

Для примера переведем 10,625₁₀ в двоичную систему:
0,625*2 = 1,25
0,250*2 = 0,5
0,5*2 = 1,0
Записав все остатки сверху вниз, получаем 10,625₁₀ = (1010), (101) = 1010,101₂

Источник

Что такое десятичная форма

ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА II

§ 38 Десятичная форма записи рациональных чисел

На практике обычно пользуются десятичной, формой записи рациональных чисел. Так, вместо 1 /₂ пишут 0,5; вместо — 3 /₈ пишут — 0,375; вместо 5 /₄ пишут 1,25 и т. д. Для простоты в дальнейшем мы будем говорить лишь о положительных и правильных дробях, то есть дробях, заключенных в интервале от 0 до 1.

5 /₁₆= 0,3125 (конечная десятичная дробь);

1 /₃ = 0,3333. (бесконечная периодическая десятичная дробь с периодом 3);

29 /₁₁₀ = 0,26363. (бесконечная периодическая десятичная дробь с периодом 63).

Период начинается либо сразу же после запятой (например, 0,333. ), либо после нескольких десятичных знаков, не входящих в период (например, 026363. ). Соответственно этому все периодические десятичные дроби разделяются на простые (такие, как 0,333. ) и смешанные (такие, как 0,26363. ).

Период бесконечной десятичной дроби, которая получается в результате деления целых чисел «уголком», может быть любым натуральным числом; исключается лишь случай, когда он составлен из одних девяток. (На строгом доказательстве этого факта мы останавливаться не будем.) Отметим еще, что любую конечную десятичную дробь можно рассматривать как бесконечную периодическую дробь с периодом 0. Например,

и т. д. Таким образом, любое рациональное число можно представить в виде бесконечной периодической десятичной дроби, период которой отличен от 9.

Верно.и обратное утверждение: любая бесконечная периодическая дробь с периодом, отличным от 9, является рациональным числом.

Доказательство этого утверждения мы отложим до § 148. А пока напомним.лишь известные из арифметики правила обращения периодических десятичных дробей в обыкновенные. Для простоты мы предположим, что все рассматриваемые нами десятичные дроби положительны и меньше единицы.

Правило 1. Для обращения простой периодической, дроби в обыкновенную нужно поступить следующим образом: в числителе поставить период десятинной дроби, а в знаменателе—число, состоящее, из девяток, взятых столько раз, сколько знаков в периоде дecятичной дроби.

Правило 2. Для обращения смешанной периодической десятичной дроби в обыкновенную нужно поступить следующим образом: в числителе взять число, стоящее в десятичной дроби до второго периода, минус число, стоящее в десятичной дроби до первого периода; в знаменателе нужно написать столько девяток, сколько цифр в периоде, и приписать к ним столько нулей, сколько цифр в исходной десятичной дроби от запятой до первого периода. Например,

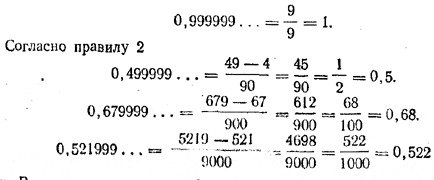
Заметим, что бесконечным периодическим дробям с периодом 9 также можно придать определенный смысл, если формально, используя правила 1 и 2, представить их в виде отношения двух целых чисел. Например, правило 1 дает

и т. д. Все приведенные здесь бесконечные периодические десятичные дроби с периодом 9 оказались ранными конечным десятичным дробям, которые получаются из данных десятичных дробей, если десятичный знак, стоящий перед первым периодом, увеличить на 1, а все последующие десятичные знаки отбросить. Можно доказать, что это относится не только к рассмотренным, но и к любым другим периодическим десятичным дробям с периодом 9. Отсюда вытекает, что любая конечная десятичная дробь может быть представлена в виде бесконечной периодической дроби двумя различными способами: с периодом 0 и с периодом 9. Например,

Это обстоятельство затрудняет изложение теории бесконечных периодических десятичных дробей. Вот почему в дальнейшем мы условимся совсем не говорить о периодических десятичных дробях с периодом 9, каждый раз заменяя их соответствующими периодическими дробями с периодом 0.

Итак, рациональные числа (и только они) представимы в виде бесконечных периодических десятичных дробей. А существуют ли бесконечные непериодические десятичные дроби? Вопрос этот решается положительно. Чтобы убедиться в этом, достаточно привести хотя бы один пример бесконечной непериодической десятичной дроби. Такой пример дает, в частности, дробь

(после запятой выписываются подряд числа 10, 100, 1000, 10000 и т. д.). Попробуйте доказать, что указанная десятичная дробь действительно является непериодической!

В следующих параграфах будут рассмотрены конкретные задачи, которые приводят нас к бесконечным непериодическим десятичным дробям.

300. Записать в виде бесконечных десятичных дробей:

301*. Данные периодические десятичные дроби обратить в обыкновенные:

а) 0,444444. ; в) 4,636363. ; д) — 2,001777. ;

303*. Почему при делении целых чисел «уголком» получаются всегда периодические дроби?

304*. Доказать, что дробь

которая получается, если после нуля выписать подряд все натуральные числа, не является периодической.

Источник

Основные сведения о десятичной системе счисления

Системы счисления. Основные понятия

Система счисления — это набор правил записи чисел посредством конечного набора цифр.

Системы счисления разделяются на:

Основание системы счисления — это количество цифр, используемых в данной системе.

Вес разряда — это отношение количественного эквивалента цифры в данном разряде к количественному эквиваленту такой же цифры в нулевом разряде:

Разряды числа нумеруются справа налево. Младший разряд имеет номер ноль. Разряды дробной части нумеруются отрицательными числами:

Что такое десятичная система счисления

Десятичная система счисления — это система счисления по целочисленному основанию 10 (0,1,2,3,4,5,6,7,8,9 арабские цифры). Она является позиционной системой счисления и наиболее распространенной.

Ученые утверждают, что использование такой распространенной системы связана с количеством пальцев на руках у человека.

Десятичные цифры используют в двоично-десятичном кодировании в двоичных компьютерах.

Алгоритм перевода чисел из любой системы счисления в десятичную

Перевести целое число с основанием q в десятичное можно с помощью следующего алгоритма:

Также можно переводить дроби с основанием q в десятичную систему счисления. Воспользуемся следующей формулой:

Примеры решения задач

Дано число в двоичной система 10011. Перевести число в десятичную систему счисления.

10011 2 = 1 ∙ 2 4 + 0 ∙ 2 3 + 0 ∙ 2 2 + 1 ∙ 2 1 + 1 ∙ 2 0 = 1 ∙ 16 + 0 ∙ 8 + 0 ∙ 4 + 1 ∙ 2 + 1 ∙ 1 = 16 + 0 + 0 + 2 + 1 = 19 10

Перевести в десятичную систему счисления число 17 из восьмеричной системы.

17 8 = 1 ∙ 8 1 + 7 ∙ 8 0 = 1 ∙ 8 + 7 ∙ 1 = 8 + 7 = 15 10

Перевести из пятеричной системы счисления число 20341 в десятичную систему.

20341 5 = 2 ∙ 5 4 + 0 ∙ 5 3 + 3 ∙ 5 2 + 4 ∙ 5 1 + 1 ∙ 5 0 = 2 ∙ 625 + 0 ∙ 125 + 3 ∙ 25 + 4 ∙ 5 + 1 ∙ 1 = 1250 + 0 + 75 + 20 + 1 = 1346 10

Число 0,F3D0 из шестнадцатеричной системы счисления перевести в десятичную систему.

Перевести в десятичную систему счисления двоичное число 101,11.

Источник

Десятичная система счисления

Всего получено оценок: 202.

Всего получено оценок: 202.

Все вычисления в математике выполняются в позиционной десятичной системе счисления. Кратко об особенностях десятичной системы можно прочитать в данной статье.

Что такое десятичная система счисления

В десятичной системе для представления чисел использует десять арабских цифр от 0 до 9, соответственно основанием десятичной системы счисления является число 10.

Историки, изучающие культуру древнего востока, в Индии обнаружили плиту с начертанием числа в позиционной десятичной системе. Возраст найденного артефакта составляет порядка 1,5 тысяч лет. Здесь же в древней Индии впервые используется ноль, как самостоятельная цифра.

Развернутая форма представления десятичного числа

Важным понятием в позиционном подходе представления чисел является понятие разряда. Различают разряды единиц, десятков, сотен, тысяч и так далее. Любое десятичное число можно представить, в так называемом развернутом виде, когда число записывается в виде суммы разрядных слагаемых, представленных в виде произведения значащей цифры разряда и числа десять в степени соответствующего разряда.

Например, десятичное число 46758 в развернутом виде будет выглядеть следующим образом:

46758 = 4 * 10^4 + 6 * 10^3 + 7 * 10^2 + 5 * 10^1 + 8 * 10^0

46758 = 4 * 10000 + 6 * 1000 + 7 * 100 + 5 * 10 + 8 * 1

Прямой перевод числа из десятичной системы

Перевод целого десятичного числа в какую-либо систему счисления выполняется путем поочередного деления самого числового значения, а затем полученных частных на основание системы счисления, в которую производится перевод.

Например, для перевода десятичного числа в двоичную систему выполняют деление на два, в восьмеричную – на восемь, в шестнадцатеричную – на шестнадцать. В принципе, десятичное число можно перевести и в пятеричную и семеричную системы, выполнив деление на пять или семь.

Выполнив первый шаг деления на, например, два, остаток запоминают, а полученное частное снова делят на основание. Эту операцию выполняют до тех пор, пока последнее частное не будет меньше или равно делителю.

Записывать сформированное число в новой системе счисления необходимо начиная с итогового частного и затем друг за другом выписывая остатки от деления от последнего к первому.

Например, прямой перевод числа 27 из десятичной системы в двоичную выполняют так:

27 / 2 = 13 и остаток 1

13 / 2 = 6 и остаток 1

6 / 2 = 3 и остаток 0

3 / 2 = 1 и остаток 1

Таким образом, 27 в двоичном формате это число 11011.

Для перевода чисел в пределах можно пользоваться таблицей соответствия десятичных и двоичных чисел

Рис. 2. Таблица соответствия двоичных и десятичных чисел.

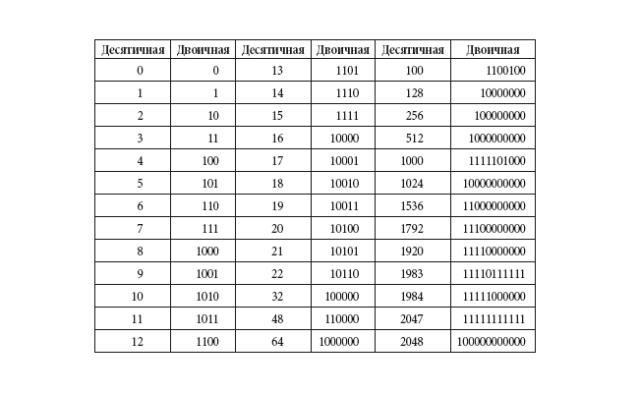
Обратный перевод числа в десятичную систему

Для перевода чисел в десятичную систему удобно пользоваться развернутой формой. При этом числовые значения записываются в виде суммы произведений цифр разрядов на основание текущей системы счисления в степени разряда.

Например, двоичное число 11011 можно представить так:

1 * 2^4 + 1 * 2^3 + 0 * 2^2 + 1 * 2^1 + 1 * 2^0 = 1 * 16 + 1 * 8 + 0 * 4 + 1 * 2 + 1 * 1 =27

Для упрощения вычислений удобно пользоваться таблицей степени двойки

Рис. 3. Степени двойки.

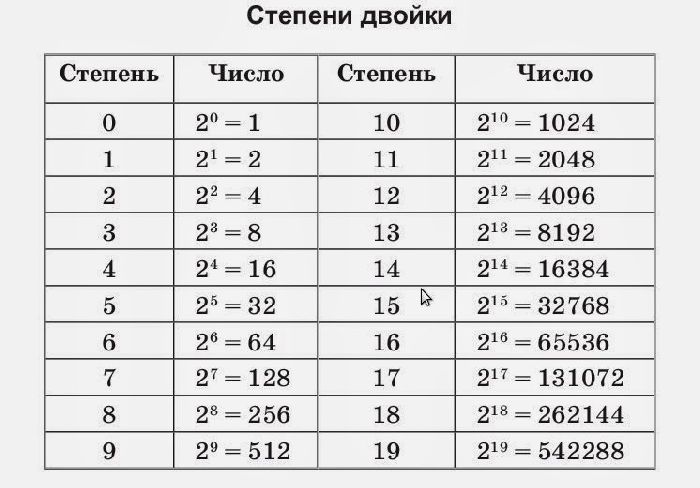
Что мы узнали?

В десятичной позиционной системе для представления числовых значений используются десять арабских цифр. Числа в такой системе можно представлять в развернутом виде. Перевод десятичных чисел в другую систему выполняется путем поочередного деления на основание новой системы счисления. Обратный перевод удобно выполнять с использованием развернутой формы записи числа.

Источник