Что такое деревья в информатике
Все что нужно знать о древовидных структурах данных
Jul 1, 2018 · 14 min read
Деревья прекрасны. Вот рисунок, который я сделал ребенком
Когда вы впервые учитесь кодировать, общепринято изучать массивы в качестве «основной структуры данных».
В конце концов, вы также изучаете хэш-таблицы. Для получения степени по «Компьютерным наукам» (Computer Science) вам придется походить на занятия по структурам данных, на которых вы узнаете о связанных списках, очередях и стеках. Эти структуры данных называются «линейными», поскольку они имеют логические начало и завершение.
Однако в самом начале и зучения деревьев и графов мы можем оказаться слегка сбитыми с толку. Нам привычно хранить данные линейным способом, а эти две структуры хранят данные совершенно иначе.
Данная статья поможет вам лучше понять древовидные структуры данных и устранить все недоразумения на их счет.
Из этой статьи вы узнаете:
Давайте начнем наше учебное путешествие 🙂
Определения
Когда вы только начинаете изучать программирование, обычно бывает проще понять, как строятся линейные структуры данных, чем более сложные структуры, такие как деревья и графы.
Деревья являются широко известными нелинейными структурами. Они хранят данные не линейным способом, а упорядочивают их иерархически.
Давайте вплотную займемся реальными примерами
Что я имею в виду, когда я говорю иерархически?
Представьте себе генеалогическое древо отношений между поколениями: бабушки и дедушки, родители, дети, братья и сестры и т.д. Мы обычно организуем семейные деревья иерархически.
Мое фамильное дерево
Приведенный рисунок — это мое фамильное древо. Тосико, Акикадзу, Хитоми и Такеми — мои дедушки и бабушки.
Тошиаки и Джулиана — мои родители.
ТК, Юдзи, Бруно и Кайо — дети моих родителей (я и мои братья).
Структура организации — еще один пример иерархии.
Структура компании является примером иерархии
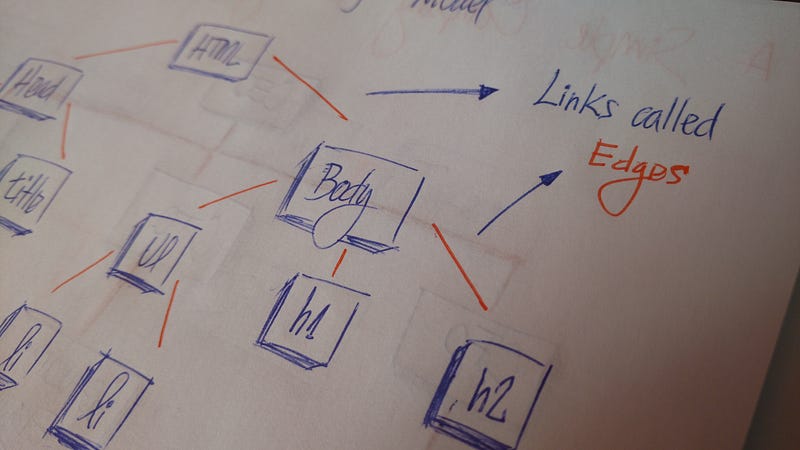
В HTML, объектная модель документа (DOM) представляется в виде дерева.
Объектная модель документа (DOM)
Техническое определение
Дерево представляет собой набор объектов, называемых узлами. Узлы соединены ребрами. Каждый узел содержит значение или данные, и он может иметь или не иметь дочерний узел.
Первый узел дерева называется корнем. Если этот корневой узел соединен с другим узлом, тогда корень является родительским узлом, а связанный с ним узел — дочерним.
Все узлы дерева соединены линиями, называемыми ребрами. Это важная часть деревьев, потому что она управляет связью между узлами.
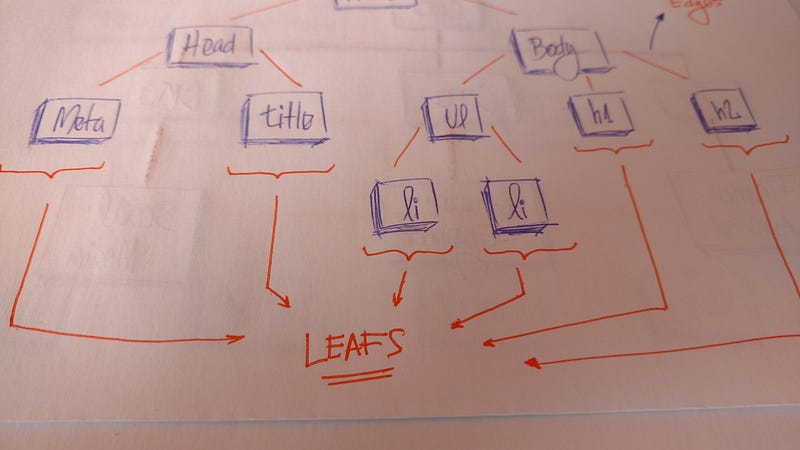
Листья — это последние узлы на дереве. Это узлы без потомков. Как и в реальных деревьях, здесь имеется корень, ветви и, наконец, листья.
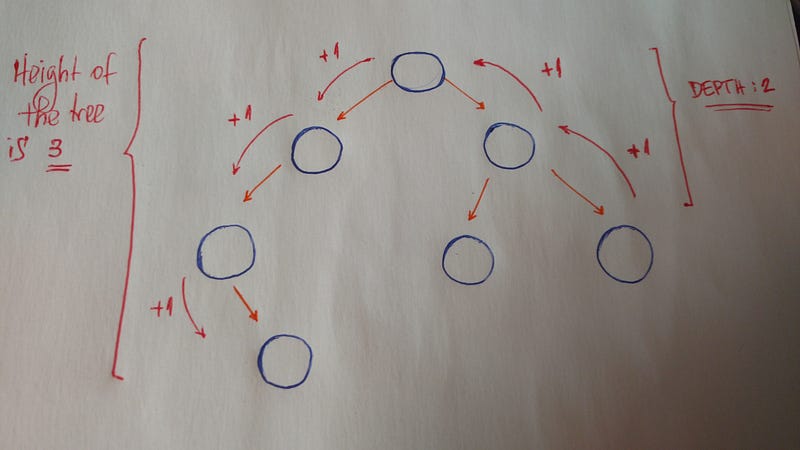
Другими важными понятиями являются высота и глубина.
Высота дерева — это длина самого длинного пути к листу.
Глубина узла — это длина пути к его корню.
Справочник терминов
Бинарные деревья
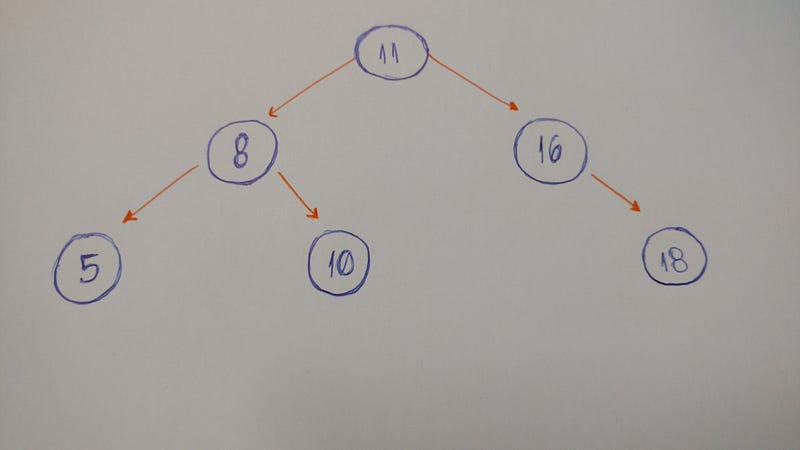
Теперь рассмотрим особый тип деревьев, называемых бинарными или двоичными деревьями.
“В информатике бинарным (двоичным) деревом называется иерархическая структура данных, в которой каждый узел имеет не более двух потомков (детей). Как правило, первый называется родительским узлом, а дети называются левым и правым наследниками.” — Wikipedia
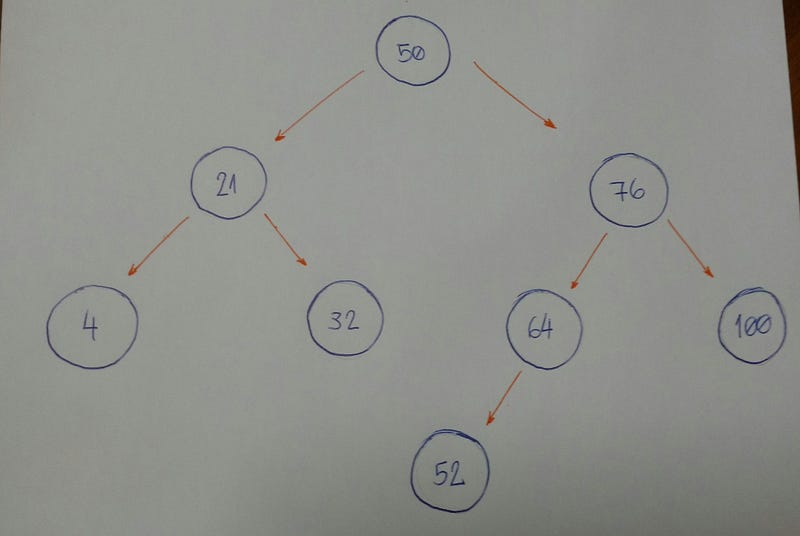
Рассмотрим пример бинарного дерева.
Давайте закодируем бинарное дерево
Как мы реализуем простое двоичное дерево, которое инициализирует эти три свойства?
Вот наш двоичный класс дерева.
Когда мы создаем наш узел, он не имеет потомков. Просто есть данные узла.
Давайте это проверим:
Перейдем к части вставки. Что нам нужно здесь сделать?
Мы реализуем метод вставки нового узла справа и слева.
Давайте это нарисуем 🙂
Вот программный код:
Еще раз, если текущий узел не имеет левого дочернего элемента, мы просто создаем новый узел и устанавливаем его в качестве left_child текущего узла. Или мы создаем новый узел и помещаем его вместо текущего левого потомка. Назначим этот левый дочерний узел в качестве левого дочернего элемента нового узла.
И мы делаем то же самое, чтобы вставить правый дочерний узел.
Но не полностью. Осталось протестировать.
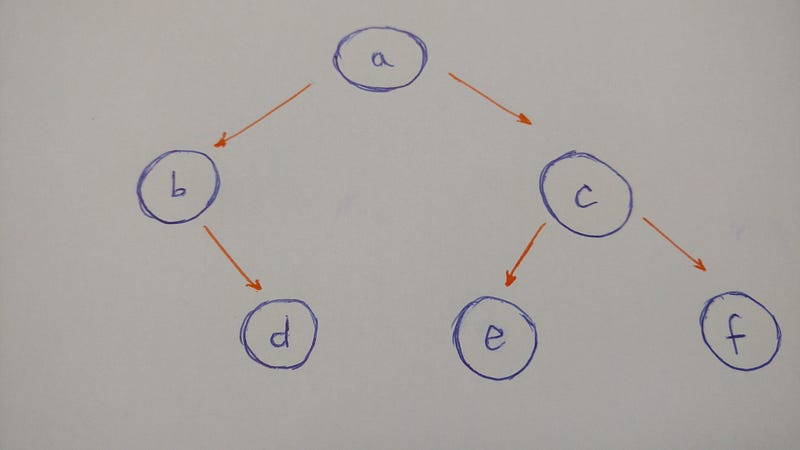
Давайте построим следующее дерево:
Подытоживая изображенное дерево, заметим:
Таким образом, вот код для нашего дерева следующий:
Теперь нам нужно подумать об обходе дерева.
У нас есть два варианта: поиск в глубину (DFS) и поиск по ширине (BFS).
• Поиск в глубину (Depth-first search, DFS) — один из методов обхода дерева. Стратегия поиска в глубину, как и следует из названия, состоит в том, чтобы идти «вглубь» дерева, насколько это возможно. Алгоритм поиска описывается рекурсивно: перебираем все исходящие из рассматриваемой вершины рёбра. Если ребро ведёт в вершину, которая не была рассмотрена ранее, то запускаем алгоритм от этой нерассмотренной вершины, а после возвращаемся и продолжаем перебирать рёбра. Возврат происходит в том случае, если в рассматриваемой вершине не осталось рёбер, которые ведут в не рассмотренную вершину. Если после завершения алгоритма не все вершины были рассмотрены, то необходимо запустить алгоритм от одной из не рассмотренных вершин.
• Поиск в ширину (breadth-first search, BFS) — метод обхода дерева и поиска пути. Поиск в ширину является одним из неинформированных алгоритмов поиска. Поиск в ширину работает путём последовательного просмотра отдельных уровней дерева, начиная с узла-источника. Рассмотрим все рёбра, выходящие из узла. Если очередной узел является целевым узлом, то поиск завершается; в противном случае узел добавляется в очередь. После того, как будут проверены все рёбра, выходящие из узла, из очереди извлекается следующий узел, и процесс повторяется.
Давайте подробно рассмотрим каждый из алгоритмов обхода.
Поиск в глубину (DFS)
DFS исследует все возможные пути вплоть до некоторого листа дерева, возвращается и исследует другой путь (осуществляя, таким образом, поиск с возвратом). Давайте посмотрим на пример с этим типом обхода.
Результатом этого алгоритма будет: 1–2–3–4–5–6–7.
Давайте разъясним это подробно.
Проход в глубь дерева, а затем возврат к исходной точке называется алгоритмом DFS.
После знакомства с этим алгоритмом обхода, рассмотрим различные типы DFS-алгоритма: предварительный обход (pre-order), симметричный обход (in-order) и обход в обратном порядке (post-order).
Предварительный обход
Именно это мы и делали в вышеприведенном примере.
1. Записать значение узла.
2. Перейти к левому потомку и записать его. Это выполняется тогда и только тогда, когда имеется левый потомок.
3. Перейти к правому потомку и записать его. Это выполняется тогда и только тогда, когда имеется правый потомок.
Структуры данных: бинарные деревья. Часть 1
Интро
Этой статьей я начинаю цикл статей об известных и не очень структурах данных а так же их применении на практике.
В своих статьях я буду приводить примеры кода сразу на двух языках: на Java и на Haskell. Благодаря этому можно будет сравнить императивный и функциональный стили программирования и увидить плюсы и минусы того и другого.
Начать я решил с бинарных деревьев поиска, так как это достаточно базовая, но в то же время интересная штука, у которой к тому же существует большое количество модификаций и вариаций, а так же применений на практике.
Зачем это нужно?
Бинарные деревья поиска обычно применяются для реализации множеств и ассоциативных массивов (например, set и map в с++ или TreeSet и TreeMap в java). Более сложные применения включают в себя ropes (про них я расскажу в одной из следующих статей), различные алгоритмы вычислительной геометрии, в основном в алгоритмах на основе «сканирующей прямой».
В этой статье деревья будут рассмотрены на примере реализации ассоциативного массива. Ассоциативный массив — обобщенный массив, в котором индексы (их обычно называют ключами) могут быть произвольными.
Ну-с, приступим
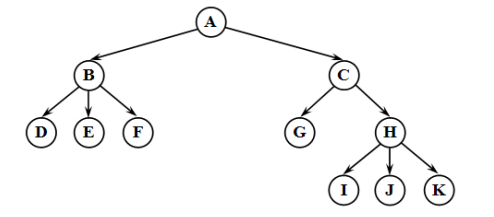
Двоичное дерево состоит из вершин и связей между ними. Конкретнее, у дерева есть выделенная вершина-корень и у каждой вершины может быть левый и правый сыновья. На словах звучит несколько сложно, но если взглянуть на картинку все становится понятным:
У этого дерева корнем будет вершина A. Видно, что у вершины D отсутствует левый сын, у вершины B — правый, а у вершин G, H, F и I — оба. Вершины без сыновей принято называть листьями.
Каждой вершине X можно сопоставить свое дерево, состоящее из вершины, ее сыновей, сыновей ее сыновей, и т.д. Такое дерево называют поддеревом с корнем X. Левым и правым поддеревьями X называют поддеревья с корнями соответственно в левом и правом сыновьях X. Заметим, что такие поддеревья могут оказаться пустыми, если у X нет соответствующего сына.
Данные в дереве хранятся в его вершинах. В программах вершины дерева обычно представляют структурой, хранящей данные и две ссылки на левого и правого сына. Отсутствующие вершины обозначают null или специальным конструктором Leaf:
Как видно из примеров, мы требуем от ключей, чтобы их можно было сравнивать между собой ( Ord a в haskell и T1 implements Comparable в java). Все это не спроста — для того, чтобы дерево было полезным данные должны храниться в нем по каким-то правилам.
Какие же это правила? Все просто: если в вершине X хранится ключ x, то в левом (правом) поддереве должны храниться только ключи меньшие (соответственно большие) чем x. Проиллюстрируем:
Что же нам дает такое упорядочевание? То, что мы легко можем отыскать требуемый ключ x в дереве! Просто сравним x со значением в корне. Если они равны, то мы нашли требуемое. Если же x меньше (больше), то он может оказаться только в левом (соответственно правом) поддереве. Пусть например мы ищем в дереве число 17:
Функция, получающая значение по ключу:
Добавление в дерево
Теперь попробуем сделать операцию добавления новой пары ключ/значение (a,b). Для этого будем спускаться по дереву как в функции get, пока не найдем вершину с таким же ключем, либо не дойдем до отсутсвующего сына. Если мы нашли вершину с таким же ключем, то просто меняем соответствующее значение. В противно случае легко понять что именно в это место следует вставить новую вершину, чтобы не нарушить порядок. Рассмотрим вставку ключа 42 в дерево на прошлом рисунке:
Лирическое отступление о плюсах и минусах функционального подхода
Если внимательно рассмотреть примеры на обоих языках, можно увидеть некоторое различие в поведении функциональной и императивной реализаций: если на java мы просто модифицируем данные и ссылки в имеющихся вершинах, то версия на haskell создает новые вершины вдоль всего пути, пройденного рекурсией. Это связано с тем, что в чисто функциональных языках нельзя делать разрушающие присваивания. Ясно, что это ухудшает производительность и увеличивает потребляемую память. С другой стороны, у такого подхода есть и положительные стороны: отсутствие побочных эффектов сильно облегчает понимание того, как функционирует программа. Более подробно об этом можно прочитать в практически любом учебнике или вводной статье про функциональное программирование.
В этой же статье я хочу обратить внимание на другое следствие функционального подхода: даже после добавления в дерево нового элемента старая версия останется доступной! За счет этого эффекта работают ropes, в том числе и в реализации на императивных языках, позволяя реализовывать строки с асимптотически более быстрыми операциями, чем при традиционном подходе. Про ropes я расскажу в одной из следующих статей.
Вернемся к нашим баранам
Теперь мы подобрались к самой сложной операции в этой статье — удалению ключа x из дерева. Для начала мы, как и раньше, найдем нашу вершину в дереве. Теперь возникает два случая. Случай 1 (удаляем число 5):
Видно, что у удаляемой вершины нет правого сына. Тогда мы можем убрать ее и вместо нее вставить левое поддерево, не нарушая упорядоченность:
Если же правый сын есть, налицо случай 2 (удаляем снова вершину 5, но из немного другого дерева):
Тут так просто не получится — у левого сына может уже быть правый сын. Поступим по-другому: найдем в правом поддереве минимум. Ясно, что его можно найти если начать в правом сыне и идти до упора влево. Т.к у найденного минимума нет левого сына, можно вырезать его по аналогии со случаем 1 и вставить его вместо удалеемой вершины. Из-за того что он был минимальным в правом поддереве, свойство упорядоченности не нарушится:
На десерт, пара функций, которые я использовал для тестирования:
Чем же все это полезно?
У читателя возможно возникает вопрос, зачем нужны такие сложности, если можно просто хранить список пар [(ключ, значение)]. Ответ прост — операции с деревом работают быстрее. При реализации списком все функции требуют O(n) действий, где n — размер структуры. (Запись O(f(n)) грубо говоря означает «пропорционально f(n)», более корректное описание и подробности можно почитать тут). Операции с деревом же работают за O(h), где h — максимальная глубина дерева (глубина — расстояние от корня до вершины). В оптимальном случае, когда глубина всех листьев одинакова, в дереве будет n=2^h вершин. Значит, сложность операций в деревьях, близких к оптимуму будет O(log(n)). К сожалению, в худшем случае дерево может выродится и сложность операций будет как у списка, например в таком дереве (получится, если вставлять числа 1..n по порядку):
К счастью, существуют способы реализовать дерево так, чтобы оптимальная глубина дерева сохранялась при любой последовательности операций. Такие деревья называют сбалансированными. К ним например относятся красно-черные деревья, AVL-деревья, splay-деревья, и т.д.
Анонс следующих серий
В следующей статье я сделаю небольшой обзор различных сбалансированных деревьев, их плюсы и минусы. В следующих статьях я расскажу о каком-нибудь (возможно нескольких) более подробно и с реализацией. После этого я расскажу о реализации ropes и других возможных расширениях и применениях сбалансированных деревьев.
Оставайтесь на связи!
Полезные ссылки
Исходники примеров целиком:
Также очень советую почитать книгу Кормен Т., Лейзерсон Ч., Ривест Р.: «Алгоритмы: построение и анализ», которая является прекрасным учебником по алгоритмам и структурам данных
Дерево как структура данных
Какую выгоду можно извлечь из такой структуры данных, как дерево? В этой статье мы расскажем о данных в виде дерева, рассмотрим основные определения, которые следует знать, а также узнаем, как и зачем используется дерево в программировании. Спойлер: бинарные деревья часто применяют для поиска информации в базах данных, для сортировки данных, для проведения вычислений, для кодирования и в других случаях. Но давайте обо всем по порядку.
Основные термины
Дерево — это, по сути, один из частных случаев графа. Древовидная модель может быть весьма эффективна в случае представления динамических данных, особенно тогда, когда у разработчика стоит цель быстрого поиска информации, в тех же базах данных, к примеру. Еще древом называют структуру данных, которая представляет собой совокупность элементов, а также отношений между этими элементами, что вместе образует иерархическую древовидную структуру.
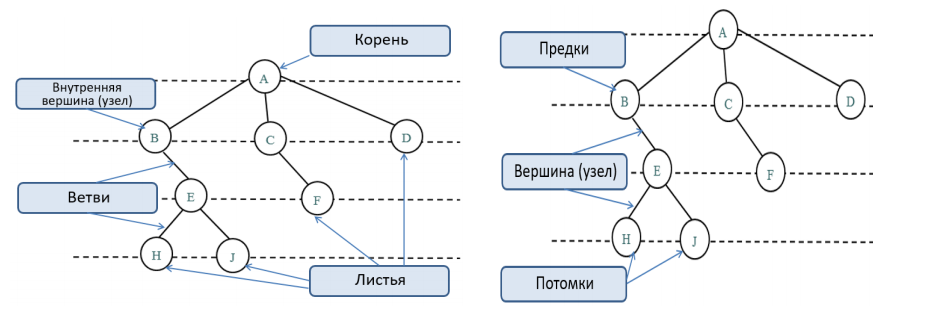
Каждый элемент — это вершина или узел дерева. Узлы, соединенные направленными дугами, называются ветвями. Начальный узел — это корень дерева (корневой узел). Листья — это узлы, в которые входит 1 ветвь, причем не выходит ни одной.
Общую терминологию можно посмотреть на левой и правой части картинки ниже:
Какие свойства есть у каждого древа:
— существует узел, в который не входит ни одна ветвь;
— в каждый узел, кроме корневого узла, входит 1 ветвь.
На практике деревья нередко применяют, изображая различные иерархии. Очень популярны, к примеру, генеалогические древа — они хорошо известны. Все узлы с ветвями, исходящими из единой общей вершины, являются потомками, а сама вершина называется предком (родительским узлом). Корневой узел не имеет предков, а листья не имеют потомков.
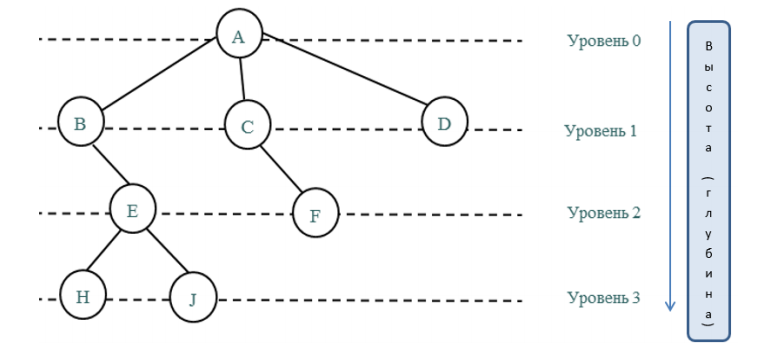
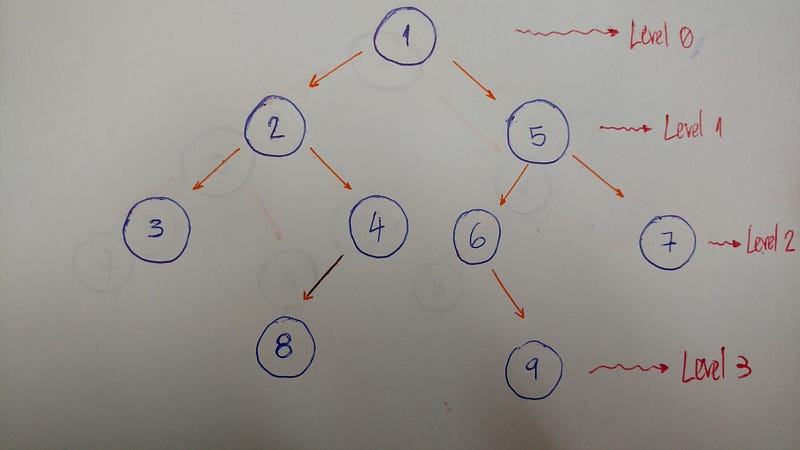
Также у дерева есть высота (глубина). Она определяется числом уровней, на которых располагаются узлы дерева. Глубина пустого древа равняется нулю, а если речь идет о дереве из одного корня, тогда единице. В данном случае на нулевом уровне может быть лишь одна вершина – корень, на 1-м – потомки корня, на 2-м – потомки потомков корня и т. д.
Ниже изображен графический вывод древа с 4-мя уровнями (дерево имеет глубину, равную четырем):
Следующий термин, который стоит рассмотреть, — это поддерево. Поддеревом называют часть древообразной структуры, которую можно представить в виде отдельного дерева.
Идем дальше. Древо может быть упорядоченным — в данном случае ветви, которые исходят из каждого узла, упорядочены по некоторому критерию.
Степень вершины в древе — это число ветвей (дуг), выходящих из этой вершины. Степень равняется максимальной степени вершины, которая входит в дерево. В этом случае листьями будут узлы, имеющие нулевую степень. По величине степени деревья бывают:
— двоичные (степень не больше двух);
— сильноветвящиеся (степень больше двух).
Деревья — это рекурсивные структуры, ведь каждое поддерево тоже является деревом. Каждый элемент такой рекурсивной структуры является или пустой структурой, или компонентом, с которым связано конечное количество поддеревьев.
Когда мы говорим о рекурсивных структурах, то действия с ними удобнее описывать посредством рекурсивных алгоритмов.
Обход древа
Чтобы выполнить конкретную операцию над всеми вершинами, надо все эти узлы просмотреть. Данную задачу называют обходом дерева. То есть обход представляет собой упорядоченную последовательность узлов, в которой каждый узел встречается лишь один раз.
В процессе обхода все узлы должны посещаться в некотором, заранее определенном порядке. Есть ряд способов обхода, вот три основные:
— прямой (префиксный, preorder);
— симметричный (инфиксный, inorder);
— обратный (постфиксный, postorder).
Существует много древовидных структур данных: двоичные (бинарные), красно-черные, В-деревья, матричные, смешанные и пр. Поговорим о бинарных.
Бинарные (двоичные) деревья
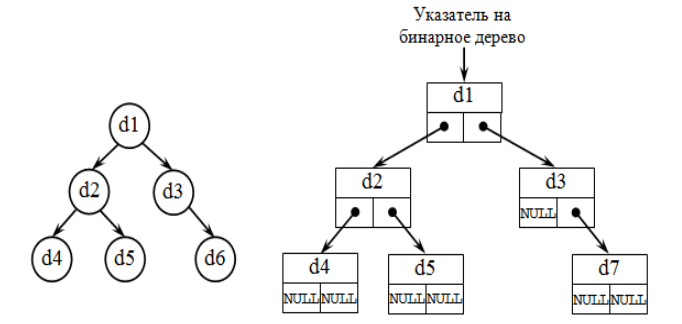
Бинарные имеют степень не более двух. То есть двоичным древом можно назвать динамическую структуру данных, где каждый узел имеет не большое 2-х потомков. В результате двоичное дерево состоит из элементов, где каждый из элементов содержит информационное поле, а также не больше 2-х ссылок на различные поддеревья. На каждый элемент древа есть только одна ссылка.
У бинарного древа каждый текущий узел — это структура, которая состоит из 4-х видов полей. Какие это поля:
— информационное (ключ вершины);
— служебное (включена вспомогательная информация, однако таких полей может быть несколько, а может и не быть вовсе);
— указатель на правое поддерево;
— указатель на левое поддерево.
Самый удобный вид бинарного древа — бинарное дерево поиска.
Что значит древо в контексте программирования?
Мы можем долго рассуждать о математическом определении древа, но это вряд ли поможет понять, какие именно выгоды можно извлечь из древовидной структуры данных. Тут важно отметить, что древо является способом организации данных в форме иерархической структуры.
В каких случаях древовидные структуры могут быть полезны при программировании:
— поиск данных в базах данных (специально построенных деревьях);
Все что нужно знать о древовидных структурах данных
Когда вы впервые учитесь кодировать, общепринято изучать массивы в качестве «основной структуры данных».
В конце концов, вы также изучаете хэш-таблицы. Для получения степени по «Компьютерным наукам» (Computer Science) вам придется походить на занятия по структурам данных, на которых вы узнаете о связанных списках, очередях и стеках. Эти структуры данных называются «линейными», поскольку они имеют логические начало и завершение.
Однако в самом начале изучения деревьев и графов мы можем оказаться слегка сбитыми с толку. Нам привычно хранить данные линейным способом, а эти две структуры хранят данные совершенно иначе.
Данная статья поможет вам лучше понять древовидные структуры данных и устранить все недоразумения на их счет.
Из этой статьи вы узнаете:
Давайте начнем наше учебное путешествие 🙂
Определения
Когда вы только начинаете изучать программирование, обычно бывает проще понять, как строятся линейные структуры данных, чем более сложные структуры, такие как деревья и графы.
Деревья являются широко известными нелинейными структурами. Они хранят данные не линейным способом, а упорядочивают их иерархически.
Давайте вплотную займемся реальными примерами
Что я имею в виду, когда я говорю иерархически?
Представьте себе генеалогическое древо отношений между поколениями: бабушки и дедушки, родители, дети, братья и сестры и т.д. Мы обычно организуем семейные деревья иерархически.
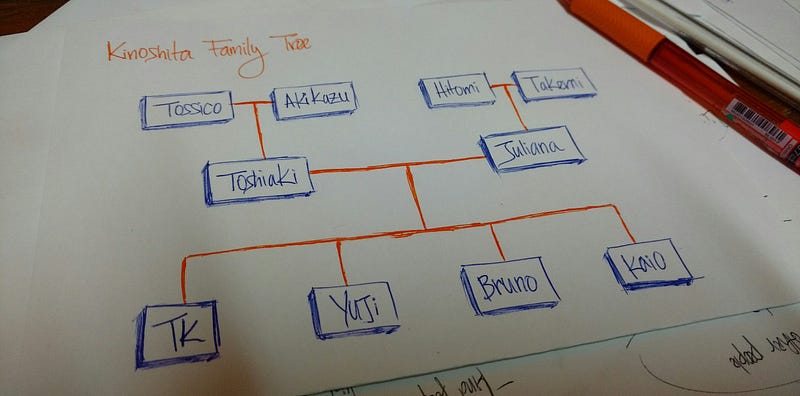
Приведенный рисунок – это мое фамильное древо. Тосико, Акикадзу, Хитоми и Такеми – мои дедушки и бабушки.
Тошиаки и Джулиана – мои родители.
ТК, Юдзи, Бруно и Кайо – дети моих родителей (я и мои братья).
Структура организации – еще один пример иерархии.
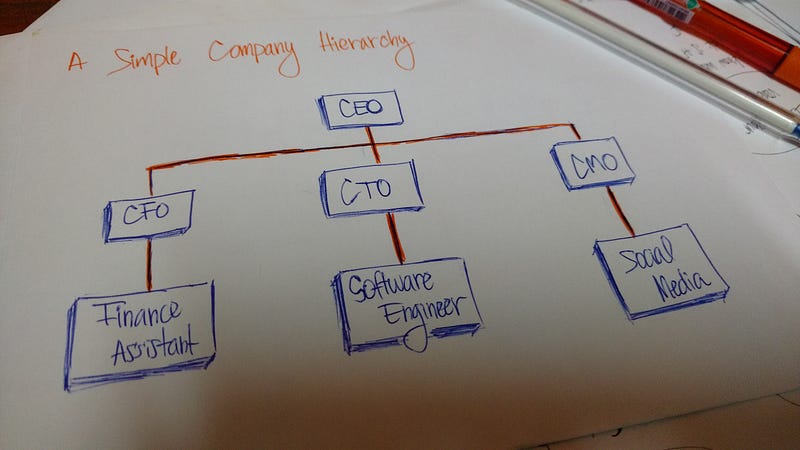
В HTML, объектная модель документа (DOM) представляется в виде дерева.
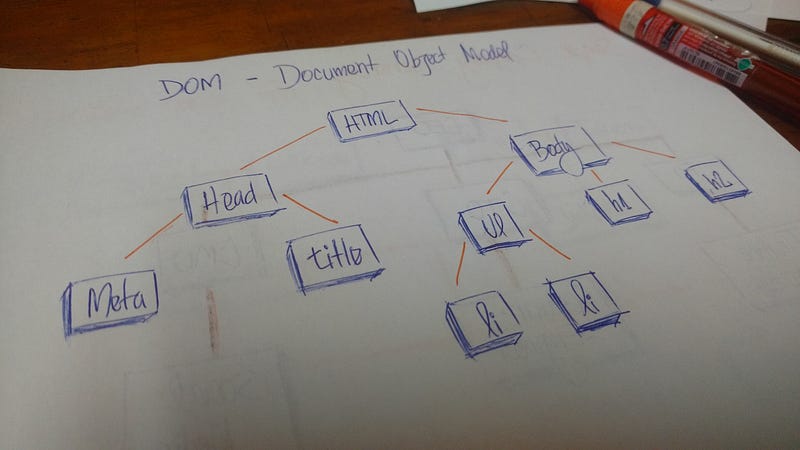
Техническое определение
Дерево представляет собой набор объектов, называемых узлами. Узлы соединены ребрами. Каждый узел содержит значение или данные, и он может иметь или не иметь дочерний узел.
Первый узел дерева называется корнем. Если этот корневой узел соединен с другим узлом, тогда корень является родительским узлом, а связанный с ним узел — дочерним.
Все узлы дерева соединены линиями, называемыми ребрами. Это важная часть деревьев, потому что она управляет связью между узлами.
Листья — это последние узлы на дереве. Это узлы без потомков. Как и в реальных деревьях, здесь имеется корень, ветви и, наконец, листья.
Другими важными понятиями являются высота и глубина.
Высота дерева — это длина самого длинного пути к листу.
Глубина узла — это длина пути к его корню.
Справочник терминов
Бинарные деревья
Теперь рассмотрим особый тип деревьев, называемых бинарными или двоичными деревьями.
Рассмотрим пример бинарного дерева.
Давайте закодируем бинарное дерево
Как мы реализуем простое двоичное дерево, которое инициализирует эти три свойства?
Вот наш двоичный класс дерева.
Когда мы создаем наш узел, он не имеет потомков. Просто есть данные узла.
Давайте это проверим:
Перейдем к части вставки. Что нам нужно здесь сделать?
Мы реализуем метод вставки нового узла справа и слева.
Давайте это нарисуем 🙂
Вот программный код:
Еще раз, если текущий узел не имеет левого дочернего элемента, мы просто создаем новый узел и устанавливаем его в качестве left_child текущего узла. Или мы создаем новый узел и помещаем его вместо текущего левого потомка. Назначим этот левый дочерний узел в качестве левого дочернего элемента нового узла.
И мы делаем то же самое, чтобы вставить правый дочерний узел.
Но не полностью. Осталось протестировать.
Давайте построим следующее дерево:
Подытоживая изображенное дерево, заметим:
Таким образом, вот код для нашего дерева следующий:
Теперь нам нужно подумать об обходе дерева.
У нас есть два варианта: поиск в глубину (DFS) и поиск по ширине (BFS).
• Поиск в глубину (Depth-first search, DFS) — один из методов обхода дерева. Стратегия поиска в глубину, как и следует из названия, состоит в том, чтобы идти «вглубь» дерева, насколько это возможно. Алгоритм поиска описывается рекурсивно: перебираем все исходящие из рассматриваемой вершины рёбра. Если ребро ведёт в вершину, которая не была рассмотрена ранее, то запускаем алгоритм от этой нерассмотренной вершины, а после возвращаемся и продолжаем перебирать рёбра. Возврат происходит в том случае, если в рассматриваемой вершине не осталось рёбер, которые ведут в не рассмотренную вершину. Если после завершения алгоритма не все вершины были рассмотрены, то необходимо запустить алгоритм от одной из не рассмотренных вершин.
• Поиск в ширину (breadth-first search, BFS) — метод обхода дерева и поиска пути. Поиск в ширину является одним из неинформированных алгоритмов поиска. Поиск в ширину работает путём последовательного просмотра отдельных уровней дерева, начиная с узла-источника. Рассмотрим все рёбра, выходящие из узла. Если очередной узел является целевым узлом, то поиск завершается; в противном случае узел добавляется в очередь. После того, как будут проверены все рёбра, выходящие из узла, из очереди извлекается следующий узел, и процесс повторяется.
Давайте подробно рассмотрим каждый из алгоритмов обхода.
Поиск в глубину (DFS)
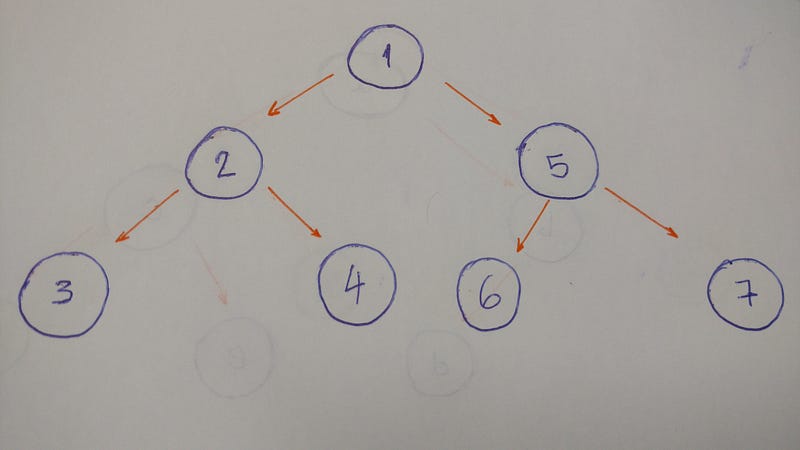
DFS исследует все возможные пути вплоть до некоторого листа дерева, возвращается и исследует другой путь (осуществляя, таким образом, поиск с возвратом). Давайте посмотрим на пример с этим типом обхода.
Результатом этого алгоритма будет: 1–2–3–4–5–6–7.
Давайте разъясним это подробно.
Проход в глубь дерева, а затем возврат к исходной точке называется алгоритмом DFS.
После знакомства с этим алгоритмом обхода, рассмотрим различные типы DFS-алгоритма: предварительный обход (pre-order), симметричный обход (in-order) и обход в обратном порядке (post-order).
Предварительный обход
Именно это мы и делали в вышеприведенном примере.
1. Записать значение узла.
2. Перейти к левому потомку и записать его. Это выполняется тогда и только тогда, когда имеется левый потомок.
3. Перейти к правому потомку и записать его. Это выполняется тогда и только тогда, когда имеется правый потомок.
Симметричный обход
Результатом алгоритма симметричного обхода для этого дерева tree в примере является 3–2–4–1–6–5–7.
Первый левый, средний второй и правый последний.
Теперь давайте напишем программный код.
Обход в обратном порядке
Первое левое, правое второе и последнее посередине.
Давайте напишем для него программный код.
Поиск в ширину (BFS)
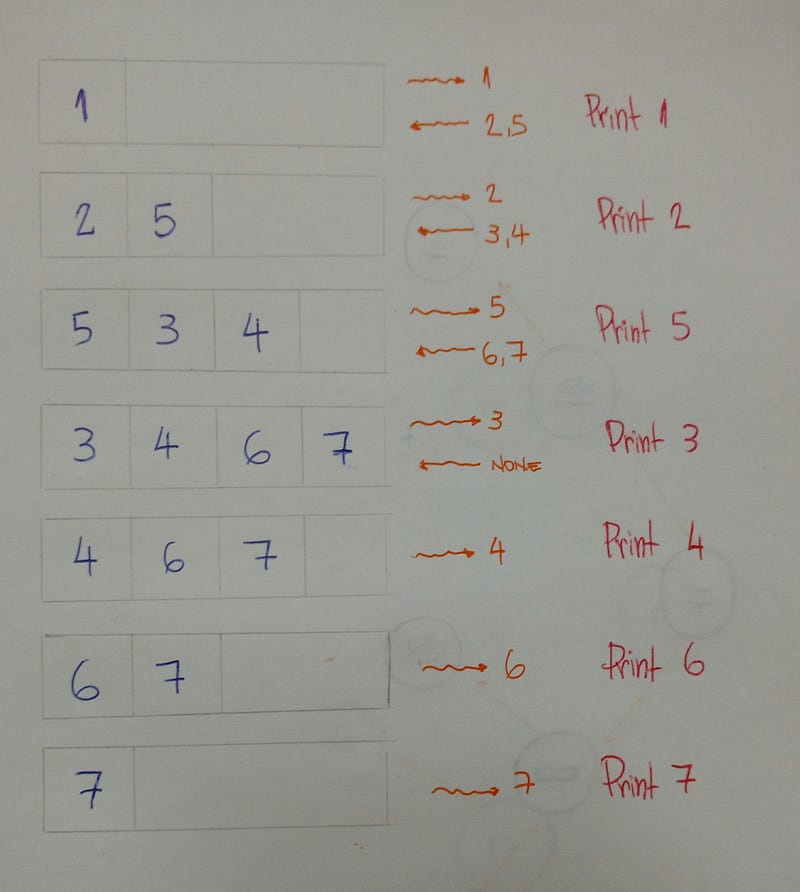
BFS алгоритм обходит дерево tree уровень за уровнем вглубь дерева.
Вот пример, помогающий лучше объяснить этот алгоритм:
Таким образом мы обходим дерево уровень за уровнем. В этом примере результатом является 1–2–5–3–4–6–7.
Теперь давайте напишем программный код.
Для реализации BFS-алгоритма мы используем данные структуры «очередь«.
Вот пошаговое объяснение.
Бинарное дерево поиска
Важным свойством поиска на двоичном дереве является то, что величина узла Binary Search Tree больше, чем количество его потомков левого элемента-потомка, но меньшее, чем количество его потомков правого элемента-потомка.
Вот детальный разбор приведенной выше иллюстрации.
Давайте напишем код для поиска на бинарном дереве!
Наступило время писать код!
Что вы увидите? Мы вставим новые узлы, поищем значения, удалим узлы и сбалансируем дерево.
Вставка: добавление новых узлов на наше дерево
Представьте, что у нас есть пустое дерево, и мы хотим добавить новые узлы со следующими значениями в следующем порядке: 50, 76, 21, 4, 32, 100, 64, 52.
Первое, что нам нужно знать, это то, что 50 является корнем нашего дерева.
Теперь мы можем начать вставлять узел за узлом.
Давайте напишем программный код.
Вроде бы все просто.
Большой частью этого алгоритма выступает рекурсия, которая находится в строке 9 и строке 13. Обе строки кода вызывают метод insert_node и используют его для своих левых и правых потомков соответственно.
Строки 11 и 15 осуществляют делают вставку для каждого потомка.
Давайте найдем значение узла … Или не найдем …
Теперь алгоритм, который мы будем строить — алгоритм поиска. Для данного значения (целое число), мы скажем, имеет ли наше дерево двоичного поиска или нет это значение.
Важно отметить, что мы определили алгоритм вставки. Сначала у нас есть наш корневой узел. Все левые узлы поддеревьев будут иметь меньшие значения, чем корневой узел. И все правильные узлы поддерева будут иметь значения, превышающие корневой узел.
Давайте рассмотрим пример.
Представьте, что у нас имеется это дерево.
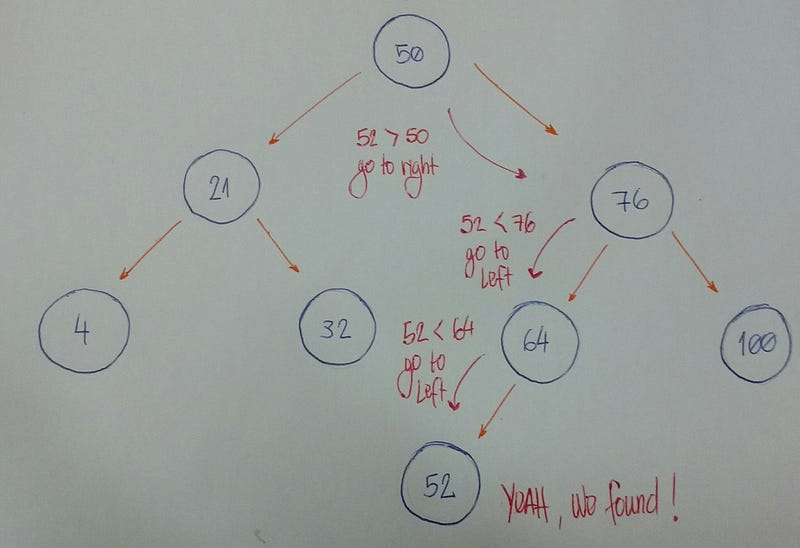
Теперь мы хотим узнать есть ли у нас узел со значением 52.
Давайте рассмотрим подробнее.
Давайте напишем код.
Разберем код подробнее:
Как нам это проверить?
Давайте создадим наше Binary Search Tree путем инициализации корневого узла значением 15.
А теперь мы вставим много новых узлов.
Да, он работает для этих заданных значений! Давайте проверим для значения, отсутствующего в нашем бинарном дереве поиска.
Стирание: удаление и организация
Удаление — более сложный алгоритм, потому что нам нужно обрабатывать разные случаи. Для заданного значения нам нужно удалить узел с этим значением. Представьте себе следующие сценарии для данного узла: у него нет потомков, есть один потомок или есть два потомка.
Если узел, который мы хотим удалить, не имеет дочерних элементов, мы просто удалим его. Алгоритм не требует реорганизации дерева.
В этом случае наш алгоритм должен заставить родительский узел указывать на узел-потомок. Если узел является левым дочерним элементом, мы делаем родительский элемент левого дочернего элемента дочерним. Если узел является правым дочерним по отношению к его родительскому, мы делаем родительский элемент правого дочернего дочерним.
Когда узел имеет 2 потомка, нужно найти узел с минимальным значением, начиная с дочернего узла. Мы поставим этот узел с минимальным значением на место узла, который мы хотим удалить.
Пришло время записать код.
Теперь давайте проверим.
Удалим узел со значением 8. Это узел без дочернего элемента.
Теперь давайте удалим узел со значением 17. Это узел с одним потомком.
Наконец, мы удалим узел с двумя потомками. Это корень нашего дерева.
Проверки успешно выполнены 🙂
Пока это все!
Мы с вами уже очень многое изучили.
Поздравляем с завершением чтения и разбора нашей насыщенной информацией и практикой статьи. Всегда довольно сложно понять новую, неизвестную еще концепцию. Но вы читатель, преодолели все трудности 🙂