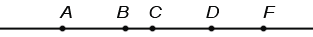Что такое дерево возможных вариантов
Комбинаторные задачи
Метод перебора
Итак, мы получили шесть возможных вариантов:
Ответ: 6 способов.
Дерево возможных вариантов
Метод отрезков
Данный метод используется только для составления всевозможных пар. Например, рассмотрим прямую, на которой обозначены точки A, B, C, D, F:
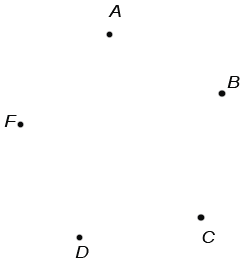
Необходимо ответить на вопрос: » Сколько отрезков изображено на рисунке?». Мы знаем, что отрезок обозначается двумя буквами, значит, для ответа на вопрос необходимо перебрать всевозможные пары букв. Это можно сделать при помощи следующей схемы: Отметим точки так, чтобы никакие 3 не лежали на одной прямой:
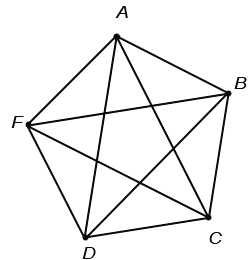
Соединим данные точки отрезками между собой. Число отрезков будет числом вариантов, то есть числом отрезков, изображенных на рисунке:
Итак, мы получили 10 отрезков, соединяющих точки.
Ответ: На рисунке 10 отрезков.
Поделись с друзьями в социальных сетях:
Методы решения комбинаторных задач
Методы решения комбинаторных задач
Перебор возможных вариантов
Простые задачи решают обыкновенным полным перебором возможных вариантов без составления различных таблиц и схем.
Задача 1.
Какие двузначные числа можно составить из цифр 1, 2, 3, 4, 5?
Ответ: 11, 12, 13, 14, 15, 21, 22, 23, 24, 25, 31, 32, 33, 34, 35, 41, 42, 43, 44, 45, 51, 52, 53, 54, 55.
Задача 2.
В финальном забеге на 100 м участвуют Иванов, Громов и Орлов. Назовите возможные варианты распределения призовых мест.
Ответ:
Вариант1: 1) Иванов, 2) Громов, 3) Орлов.
Вариант2: 1) Иванов, 2) Орлов, 3) Громов.
Вариант3: 1) Орлов, 2) Иванов, 3) Громов.
Вариант4: 1) Орлов, 2) Громов, 3) Иванов.
Вариант5: 1) Громов, 2) Орлов, 3) Иванов.
Вариант6: 1) Громов, 2) Иванов, 3) Орлов.
Задача 3.
В кружок бального танца записались Петя, Коля, Витя, Олег, Таня, Оля, Наташа, Света. Какие танцевальные пары девочки и мальчика могут образоваться?
Дерево возможных вариантов
Задача 4.
Какие трехзначные числа можно составить из цифр 0, 2, 4?
Решение. Построим дерево возможных вариантов, учитывая, что 0 не может быть первой цифрой в числе.
Ответ: 200, 202, 204, 220, 222, 224, 240, 242, 244, 400, 402, 404, 420, 422, 424, 440, 442, 444.
Ответ: На рисунке перечислены все 12 возможных вариантов путешествия школьных туристов.
Задача 6.
Запишите все возможные варианты расписания пяти уроков на день из предметов: математика, русский язык, история, английский язык, физкультура, причем математика должна быть вторым уроком.
Ответ: Всего 24 возможных варианта:
Презентация на тему «Комбинаторные задачи. Дерево возможных вариантов»
Описание презентации по отдельным слайдам:
Комбинаторные задачи: дерево возможных вариантов
ИМЯ УРОКА: КОМБИНАТОРИКА ДЕВИЗ УРОКА: «УСЛЫШАЛ – ЗАБЫЛ, УВИДЕЛ – ЗАПОМНИЛ, СДЕЛАЛ – ПОНЯЛ» КИТАЙСКАЯ ПОГОВОРКА
В странных русских сказаниях повествуется, как богатырь или другой добрый молодец, доехав до распутья, читает на камне: Вперёд поедешь – голову сложишь. Налево поедешь – меча лишишься. А дальше говорится, как он выходит из того положения, в которое попал в результате выбора. Направо поедешь – коня потеряешь. Но выбирать разные пути или варианты приходится и современному человеку. Эти пути и варианты складываются в самые разнообразные комбинации.
Что такое КОМБИНАТОРИКА? Задачи, в которых требуется осуществить перебор всех возможных вариантов, или, как обычно говорят в таких случаях, всех возможных комбинаций, называют комбинаторными. Область математики, изучающая комбинаторные задачи, называется комбинаторикой. Комбинаторика – раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчинённых тем или иным условиям, можно составить.
Задача №1 Запишите все трёхзначные числа, для записи которых употребляются только цифры 1 и 2. 1 2 1 1 2 2 1 1 1 1 2 2 2 2 Ответ: 111, 112, 121, 122, 211, 212, 221, 222 – восемь чисел. Такой метод решения комбинаторных задач называется деревом выбора(дерево возможных вариантов)
Задача №2 Запишите все трёхзначные числа, для записи которых употребляются только цифры 0,7.
ЗАДАЧА 3 В 5 «А» классе в среду 4 урока: математика, информатика, русский язык, английский язык. Сколько можно составить вариантов расписания на среду? Решение: построим картину-схему. Для удобства закодируем названия предметов: математика – м, информатика – и, русский язык – р, английский язык – а.
РЕШЕНИЕ ЗАДАЧИ 3 Расписание 1 урок м и р а 2 урок и р а м р а м и а м и р 3 урок р а и а и р р а м а м р и а м а м и и р м р м и 4 урок а р а и р и а р а м р м а и а м и м р и р м и м Ответ: 24 варианта: мира, миар, мриа, мраи, маир, мари, имра, имар, ирма, ирам, иамр, иарм, рмиа, рмаи, рима, риам, рами, раим, амир, амри, аимр, аирм, арми, арим.
Построенная схема напоминает перевернутое дерево: от ствола («расписание») отходят ветки, сначала четыре (м, и, р, а), от каждой из четырех веток – еще по три, затем еще по две и еще по одной. Видимо поэтому такую схему называют деревом возможных вариантов. Дерево возможных вариантов можно считать геометрической моделью рассматриваемой ситуации.
Можно решить Задачу 3 короче, если применить правило умножения. Существует 4 варианта выбора первого урока. Для выбора второго урока есть только три варианта, так как один из четырех уроков мы уже выбрали. Тогда для третьего урока существует два варианта, а для четвертого только один. Применив правило умножения, получим 4 ∙ 3 ∙ 2 ∙1= 24 Ответ: 24 варианта.
Задача №5 В классе 15 мальчиков и 10 девочек. Сколькими способами можно выбрать двух дежурных(одну девочку и одного мальчика)?
ЗАДАЧА 2. В 6 классе в четверг 5 уроков: математика, информатика, русский язык, английский язык, физкультура. а) Сколько имеется вариантов расписания при условии, что физкультура – последний урок? б) Сколько имеется вариантов расписания при условии, что физкультура – последний урок, а математика – первый?
ЗАДАЧА 2 (ПРОДОЛЖЕНИЕ). В 6 классе в четверг 5 уроков: математика, информатика, русский язык, английский язык, физкультура. в) Сколько всего можно составить вариантов расписания на четверг? г) Сколько времени потратит завуч на запись всех вариантов, если известно, что на запись одного варианта у него уходит 30 секунд?
Задача №1 Запишите все трёхзначные числа, для записи которых употребляются только цифры 0,7. Задача №2 Сколько двузначных чисел можно составить, используя цифры 1, 4 и 7? Нарисуйте дерево выбора на альбомном листе. Задача №3 Составьте комбинаторную задачу, которая решается с помощью правила умножения. Сделайте к ней рисунок. Задача № 4 Тренер попросил Филю составить трехзначное число из цифр 1, 2, 3, 4, причем цифры в числе могут повторяться. Сколько чисел может составить Филя? Задача № 5 Тренер попросил Филю составить трехзначное число из цифр 1, 2, 3, 4 так, чтобы цифры в числе не повторялись. Сколько чисел может составить Филя? Домашнее задание
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Ищем педагогов в команду «Инфоурок»
Номер материала: ДБ-409677
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Поставщики интернета для школ будут работать с российским оборудованием
Время чтения: 1 минута
В России утвердили новый порядок формирования федерального перечня учебников
Время чтения: 1 минута
В Минпросвещения рассказали о формате обучения школьников после праздников
Время чтения: 1 минута
В России стартует пилотный проект по реабилитации детей-инвалидов
Время чтения: 2 минуты
Минздрав включил вакцинацию подростков от ковида в календарь прививок
Время чтения: 1 минута
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Тема урока: Правило умножения и дерево возможных вариантов
Преподаватель математики ПУ № 11
Тема урока: Правило умножения и дерево возможных вариантов.
— научить учащихся подсчитывать количество возможных вариантов по правилу умножения;
— воспитывать внимательность и умение анализировать результаты.
б)позволяет всё учесть, ничего не пропустив.
Задача №1. Составить двузначные числа из цифр 2,5 и 9.
 |  |  |
первая цифра 2 5 9
 |  |  |
Подсчитаем количество решений по правилу умножения:3×3=9

 |  |
Нижний Новгород т п
 |  |
Москва с т п а с т п а
Варианты путешествия: тс, тт, тп, та, пс, пт, пп, па.
Таким образом, имеется 8 возможных способов добраться из Волгограда в Нижний Новгород, а затем в Москву. Из них можно выбрать подходящий по времени и стоимости.
По правилу умножения: 2×4=8.
Задача №3. В палатке имеется три сорта мороженого: рожок (р), брикет (б), эскимо (э). Маша и Саша решили купить по одной порции. Сколько вариантов такой покупки существует?
 |
 |  |  |
Выбор Саши б р э б р э б р э
Варианты покупки: бб, бр, бэ, рб, рр, рэ, эб, эр, ээ.
Таким образом, имеется 9 вариантов покупки мороженого.
По правилу умножения: 3×3=9.
В-1. Пусть Маша хочет купить себе две порции мороженого.
(В решении варианты бр и рб, бэ и эб, рэ и эр одиноковы. Остаётся 6 вариантов)
В-2. Пусть Маша хочет купить две порции разного сорта мороженого.
В решении варианты бб, рр, ээ не подходят. Остаётся 3 варианта)
Задача №4. Данила, Андрей и Наташа собрались потренироваться в бросании мяча в баскетбольную корзину. У них только один мяч, и им надо договориться, кто за кем будет бросать мяч. Сколькими способами они могут занять очередь друг за другом?
 |

Второй Д А Н А Н Д
 |  |  |  |  |  |
Третий А Д А Н Д Н
Варианты очереди: НДА, НАД, ДНА, ДАН, АНД, АДН.
Таким образом, у ребят имеется 6 различных вариантов очереди.
По правилу умножения: 3×2=6.
 | |
 |  |

 |  |  |  |  |  |  |  |  |
Ш1 ш2 ш3 ш1 ш2 ш 3 ш1 ш2 ш3 ш1 ш 2 ш3
Есть варианты нарядов для мишки: ф1ш1, ф1ш2, ф1ш3, ф2ш1, ф2ш2, ф2ш3, ф3ш1, ф3ш2, ф3ш3,ф4ш1, ф4ш2, ф4ш3. Всего 12 вариантов.
Получается, что у мишки больше нарядов.
Задача №6. Составить дерево вариантов для решения задачи.
В коридоре три лампочки. Сколько имеется различных способов освещения коридора?




 |
Третья третья третья третья
Можно решить задачу с помощью правила умножения.
Теперь сформулируем правило умножения:
Для того, чтобы найти число всех возможных исходов независимого проведения двух испытаний А и В, следует перемножить число всех исходов испытаний А и число всех исходов испытаний В.
Задача №7. Сколько четных двузначных чисел можно составить из цифр 0,1,2,4,5,9? Решить задачу с помощью правила умножения.
(Всего 15 чисел. 5×3=15)
3. Итог занятия. ( о значении использования дерева вариантов при решении комбинаторных задач).
4. Задание на дом. Составить задачу по профессии, при решении которой используется дерево вариантов.
Элементы комбинаторики
Разделы: Математика
Ход урока
1. Повторение ранее изученных отдельных вопросов, понятий и определений, необходимых для успешного усвоения нового материала
2. Объяснение нового материала
В старинных русских сказаниях повествуется, как богатырь или другой добрый молодец, доехав до распутья, читает на камне: “Вперед поедешь – голову сложишь, направо поедешь – коня потеряешь, налево поедешь – меча лишишься”. А дальше уже говорится, как он выходит из того положения, в которое попал в результате выбора. Но выбирать разные пути или варианты приходится и современному человеку. Эти пути и варианты складываются в самые разнообразные комбинации. И целый раздел математики, именуемый комбинаторикой, занят поисками ответов на вопросы: сколько всего есть комбинаций в том или ином случае, как из всех этих комбинаций выбрать наилучшую.
Люди, которые умело владеют техникой решения комбинаторных задач, а, следовательно, обладают хорошей логикой, умением рассуждать, перебирать различные варианты решений, очень часто находят выходы, казалось бы, из самых трудных безвыходных ситуаций. Примером мог бы послужить сказочный герой Барон Мюнхгаузен, который находил выход из любой сложной и трудной ситуации.
Но и в жизни эти умения очень часто помогают человеку. Вот один случай умелого решения комбинаторной задачи.
Спор затянулся, суп успел простыть, а за стол никто не садился.
Примирил всех официант, обратившийся к ним с такой речью:
Молодые друзья мои, оставьте ваши пререкания. Сядьте за стол как кому придется и выслушайте меня.
Все сели как попало. Официант продолжал:
Пусть один из вас запишет, в каком порядке вы сейчас сидите. Завтра вы снова явитесь сюда пообедать, и разместитесь уже в ином порядке. Послезавтра сядете опять по-новому и т.д., пока не перепробуете всех возможных размещений. Когда же придет черед вновь сесть так, как сидите вы здесь сегодня, тогда, обещаю торжественно, я начну ежедневно угощать вас бесплатно самыми изысканными обедами.
Предложение понравилось. Решено было ежедневно собираться в этом ресторане и перепробовать все способы размещения за столом, чтобы скорее начать пользоваться бесплатными обедами.
Однако им не пришлось дождаться этого дня. И вовсе не потому, что официант не исполнил обещания, а потому, что число всех возможных размещений за столом чересчур велико. Оно равняется, ни мало, ни много, 3628800. Такое число дней составляет, как нетрудно сосчитать, почти 10 тысяч лет! Это покажется на первый взгляд невероятным, но так оно и есть!
Эти методы носят следующие названия: метод перебора, дерево выбора (дерево возможных вариантов), и правило умножения.
Или, комбинаторика – раздел математики, в котором изучается, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов.
Задачей комбинаторики можно считать задачу размещения объектов по специальным правилам и нахождение числа способов таких размещений.
Задача 1. Сколько двузначных чисел можно составить, используя цифры 1, 4 и 7?
Решение. Для того чтобы не пропустить и не повторить ни одно из чисел, будем выписывать их в порядке возрастания. Сначала запишем числа, начинающиеся с цифры 1, затем с цифры 4 и, наконец, с цифры 7. Получаем следующий расклад.
Таким образом, из трех данных цифр можно составить всего 9 различных двузначных чисел.
Однако существует единый подход к решению самых разных комбинаторных задач с помощью составления специальных схем. Внешне такая схема напоминает дерево, отсюда название – дерево возможных вариантов. При правильном построении дерева ни один из возможных вариантов решения не будет потерян.
Вернемся к задаче о составлении двузначных чисел из цифр 1, 4 и 7. Для ее решения можно построить специальную схему.
Эта схема действительно похожа на дерево, правда, «вверх ногами» и без ствола. Знак “*” изображает корень дерева, ветви дерева – различные варианты решения. Чтобы получить двузначное число, надо сначала выбрать первую его цифру, а для нее есть три варианта: 1, 4 или 7. Поэтому из точки * проведены три отрезка и на концах поставлены цифры 1, 4 и 7.
Теперь надо выбрать вторую цифру, а для этого также есть три варианта: 1, 4 или 7. Поэтому от каждой первой цифры проведено по три отрезка, на концах которых снова записано 1, 4 или 7. Итак, получено всего 9 различных двузначных чисел. Других двузначных чисел из этих трех цифр составить невозможно.
В последствии, мы рассмотрим, как построение дерева помогает решить самые разные комбинаторные задачи.
Дополнительная подзадача: Сколько двузначных чисел можно составить, используя цифры 1, 4 и 7, если цифры десятков и единиц не повторяются?
Задача 2. Сколько трехзначных чисел можно составить, используя цифры 3 и 5?
Задача 3. Туристическая фирма планирует посещение туристами в Италии трех городов: Венеции, Рима и Флоренции. Сколько существует вариантов такого маршрута?
Обозначим города их первыми буквами. Тогда код каждого маршрута будет состоять из трех букв: В, Р и Ф, каждая из которых должна быть использована только один раз, например, ВФР или ФРВ.
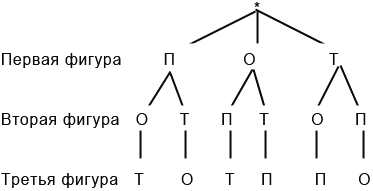
Варианты путешествия получаются следующие: ВРФ, ВФР, РВФ, РФВ, ФВР, ФРВ, что хорошо видно из дерева вариантов.
Путешествие можно начинать в любом из трех городов. Если первой посетить Венецию, то затем можно поехать в Рим или во Флоренцию. Если вторым посетить Рим, то третьей будет Флоренция, если второй будет Флоренция, то третьим будет Рим. Это первые два варианта путешествия.
Таким образом, всего существует 6 вариантов путешествия.
Задача 4. При встрече 8 приятелей обменялись рукопожатиями. Сколько всего было сделано рукопожатий?
Дадим каждому из приятелей номер – от 1 до 8. Тогда каждое рукопожатие можно закодировать двузначным числом. Например, 47 – это рукопожатие между приятелями с номерами 4 и 7.
Ясно, что среди кодов рукопожатий у нас не появится, например, 33 – это означало бы, что один из друзей пожал руку сам себе. Кроме того, такие коды, как, например, числа 68 и 86, означают одно и то же рукопожатие, а значит, учитывать надо только одно из них.
Договоримся, что из чисел, кодирующих одно и то же рукопожатие, мы всегда будем учитывать меньшее. Поэтому из чисел 68 и 86 надо выбрать 68.
Коды рукопожатий естественно выписывать в порядке возрастания. Для подсчета их удобно расположить треугольником.
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 23 | 24 | 25 | 26 | 27 | 28 | |
| 34 | 35 | 36 | 37 | 38 | ||
| 45 | 46 | 47 | 48 | |||
| 56 | 57 | 58 | ||||
| 67 | 68 | |||||
| 78 |
Число кодов равно: 7 + 6 + 5 + 4 + 3 + 2 + 1 = 28. Таким образом, всего было сделано 28 рукопожатий.
Задача 5. Служитель зоопарка должен дать зайцу два различных овоща. Сколькими различными способами он может это сделать, если у него есть морковь, свекла и капуста?
В итоге получаем 6 вариантов при учете, что мы делаем различие между МС и СМ и другими аналогичными парами. Но, если смотреть на то, что три из них эквивалентны трем другим парам (МС – СМ, МК – КМ, СК – КС), то получаем, что различных вариантов только три.
Задача 6. В спортивном лагере “Орленок” собирались проводить первенство по футболу. Незадолго до начала соревнований к начальнику лагеря пришел вожатый, который должен был судить встречи, и сказал: “Иван Владимирович! У нас на складе есть трусы и майки только трех цветов: белого, черного и синего. А команд у нас восемь. Как быть?” – “Да совсем просто, Леня! – ответил тот.– Ведь необязательно, чтобы майки и трусы были одного цвета. Можно одну команду одеть в синие майки и белые трусы, а другую – в белые майки и синие трусы. Вот игроки и увидят, где свой, а где соперник”. – “А хватит ли таких комбинаций на восемь команд?” – «Не только хватит, еще одна останется про запас».
Посмотрим на табличку.
Здесь первая буква показывает цвет майки, а вторая – цвет трусов. Можно видеть, что получилось девять различных комбинаций, так что все в порядке.
Составляя такие таблицы, можно найти число комбинаций и в случае, когда, например, есть майки различных пяти цветов, а трусы – четырех цветов. В этом случае в таблице будет пять строк и четыре столбца, а потому общее число комбинаций окажется равным 4 x 5, то есть 20. Вообще, если имеются майки т различных цветов и трусы п различных цветов, то общее число комбинаций для составления формы играющих команд равно т x п.
Полученный результат верен и тогда, когда комбинируются не майки с трусами, а, например, ложки с вилками. Он гласит:
Если надо выбрать пару вещей, причем первую вещь можно выбрать m способами, а вторую n способами, то пару можно выбрать m? n способами.
Бывает, что надо выбрать не две, а три или четыре вещи. Тогда число комбинаций ищут похожим образом: смотрят, сколькими способами можно выбрать каждую вещь, и перемножают полученные числа. Поэтому правило называют правилом произведения (или правило умножения).
Вернемся теперь к первой задаче о комбинациях, которую мы решали, к задаче о выборе формы для футболистов. Чтобы решить ее, была составлена таблица из трех строк и трех столбцов. Но если бы надо было еще выбирать цвет бутс, то пришлось бы составлять не одну, а несколько таблиц – по одной для каждого цвета бутс. Поэтому, в этом случае, удобнее было бы изображать разные варианты выбора с помощью дерева возможных вариантов.
Такие деревья мысленно воображают себе шахматисты, выбирая наилучший ход в трудной позиции. Каждая полоса соответствует полуходу (ходу за белых или за черных). И думает шахматист: если я пойду так, а противник ответит так, а потом я пойду так, а он ответит так, то какой же ход мне выбрать? Мы уже видели, что с увеличением числа полос количество возможностей очень быстро возрастает. Поэтому пройти по всем веточкам дерева расчета бывает очень трудно, а иногда даже невозможно.
Со всем этим столкнулись ученые, составлявшие шахматные программы для вычислительных машин. Им удалось справиться со всеми трудностями, и теперь уже некоторые вычислительные машины играют сильнее мастера.
Задача 7. В том же спортивном лагере повар умел готовить четыре различных супа: щи, борщ, молочный суп с лапшой и фасолевый суп. Мясных блюд он умел делать пять: котлеты, зразы, шницели, биточки и суфле. При этом, к каждому мясному блюду он умел делать три гарнира: гречневую кашу, макароны и картофельное пюре. А на сладкое он готовил тоже три блюда: компот, кисель или печеные яблоки. Сколько различных обедов умел готовить этот повар?
Если вы разобрались в правиле произведения, то ответ найдете сразу: повар умел готовить 4 x 5 x 3 x 3, то есть 180 различных обедов. Так что он мог ни разу не повторить обеда за три смены.
Задача 8. В одном городе были трехзначные велосипедные номера. Но велосипедисты попросили, чтобы в этих номерах не встречались цифры 0 и 8, потому что первая из них похожа на вытянутое колесо, ну, а что значит для велосипедиста восьмерка колеса, знает каждый. Хватит ли им номеров, если в этом городе велосипеды имеют 710 человек?
Чтобы решить эту задачу, будем составлять номера следующим образом. Сначала выберем цифру сотен. Так как цифры 0 и 8 запретны, то остается 8 различных возможностей, а именно 1, 2, 3, 4, 5, 6, 7, 9. Столько же возможностей и для выбора цифры десятков, и для выбора цифры единиц. А тогда по правилу произведения получаем, что общее число велосипедных номеров, которые можно было выдать в этом городе, равно 8 x 8 x 8, то есть 512. Так что на всех обладателей велосипедов номеров не хватило. Поэтому пришлось велосипедистам смягчить свои пожелания. Они согласились на цифру 0. После этого число номеров стало равно 9 x 9 x 9, то есть 729, и их хватило на всех.
Чтобы решить эту задачу, будем сажать ребят в порядке алфавита. Первым выбирал Андрей. Он мог сесть на любого из шести зверей, так что у него было 6 возможностей выбора. Но когда он занял свое место. Боре остались лишь 5 возможностей – одно место было уже занято. Точно так же Вите остались 4 варианта выбора, Грише – 3, Диме – 2, а когда садился на карусель Женя, ему оставалось только одно свободное место.
А теперь по правилу произведения находим, сколькими способами могли сесть за карусель ребята: 6 x 5 x 4 x 3 x 2 x 1. В математике такое произведение обозначают 6! и называют “6-факториал”. Перемножая эти числа, получаем ответ 720. Так что, если даже они катались в день по 20 раз, то им пришлось бы больше месяца ходить каждый день в парк.
Если бы и ребят, и мест на карусели было не 6, а 8, то пришлось бы перемножать числа от 1 до 8. Это произведение равно уже 40 320. А для десятиместной карусели и десяти ребят получается более 3 миллионов вариантов.
В другой раз на ту же карусель пришли только четверо ребят: Андрей, Боря, Витя и Гриша. Узнаем, сколькими способами могут они сесть на нее. По правилу произведения надо перемножить лишь четыре числа: 6, 5, 4 и 3. Получится ответ 360. А если бы трое ребят решили перебрать все способы катания на десятиместной карусели, то умножать пришлось бы только три числа: 10, 9 и 8.
Задача 10. Хоккейная комбинация. На поле 5 игроков. Начал комбинацию игрок № 1, продолжили игроки с другими номерами, а забил гол игрок № 5. Каждый хоккеист ударил по шайбе только один раз. На рисунке с помощью стрелок изображен один из возможных вариантов передачи шайбы между игроками в данной комбинации. Изобразите в тетради все другие возможные варианты передачи шайбы.
3. Закрепление нового материала
1. Андрей зашел в магазин, чтобы купить майки. В магазине оказались майки четырех цветов: белые, голубые, красные, черные.
а) Сколько вариантов покупки есть у Андрея, если он хочет купить две майки?
Подсказка: обозначьте цвета маек буквами Б, Г, К, Ч. Запишите все возможные варианты покупки, осуществляя их перебор в алфавитном порядке.
б) Сколько вариантов покупки есть у Андрея, если он хочет купить две майки разного цвета?
2. В турнире по настольному теннису участвовали 5 человек.
а) Сколько было сыграно партий, если каждый участник сыграл с остальными по одной партии?
3. В шестом классе изучается 8 предметов. Сколько различных вариантов расписания можно составить на понедельник, если в этот день должно быть 5 уроков и все разные?
Подсказка: на первом уроке можно провести любой из 8 предметов, на втором уроке – любой из оставшихся 7 предметов, на третьем уроке …
4. В магазине имеется четыре типа диванных подушек: круглые, овальные, прямоугольные и треугольные. Сколько вариантов покупки имеется у покупателя, который хочет приобрести две подушки?
Решите задачу, закончив построение дерева возможных вариантов.
5. Выпишите все трехзначные числа, используя при записи каждого числа цифры 1, 2, 3, причем каждую из них только один раз.
6. Фирма владеет четырьмя магазинами. Кассир магазина № 1 должен объехать остальные магазины, чтобы собрать выручку, и вернуться обратно. Какой из возможных маршрутов самый короткий?
7. В классе три человека хорошо поют, двое других играют на гитаре, а еще один умеет показывать фокусы. Сколькими способами можно составить концертную бригаду из певца, гитариста и фокусника?
8. Имеется 3 вида конвертов и 4 вида марок. Сколько существует вариантов выбора конверта с маркой?
9. В буфете есть четыре сорта пирожков. Сколькими способами ученик может себе купить два пирожка? два разных пирожка?
10. Сколько существует шестизначных чисел, у которых:
б) последняя цифра – четная;
в) на нечетных местах стоят нечетные цифры;
г) на нечетных местах стоят четные цифры?
11. Четыре друга купили билеты на один и тот же поезд. При этом оказалось, что два билета в один вагон, а два в другой. Из скольких вариантов посадки в два вагона им придется выбирать?
12. В четверг в первом классе должно быть три урока: русский язык, математика и физкультура. Сколько различных вар антов расписания можно составить на этот день?
13. В палатке имеется три сорта мороженого: рожок, брикет и эскимо. Наташа и Данила решили купить по одной порции. Сколько существует вариантов такой покупки?
14. Проводится олимпиада по биологии. Для подарков участникам приготовили различные растения: кактусы, фикусы, лимоны, герань. Сколько различных призов можно из них составить, если каждому победителю решено давать по два любых растения? Как изменится решение задачи, если призы можно составлять только из двух разных растений?
15. Запишите все трехзначные числа, которые можно составить из цифр 2, 5, 9, используя при записи числа каждую цифру только один раз. Сколько всего таких чисел можно составить?
16. Наташа сшила кукле десять разных платьев, а Даша сшила своему мишке трое штанишек и четыре футболки. Как вы думаете, у кого больше разных нарядов – у куклы или у мишки?
17. Для начинки пирогов у Наташи есть капуста, яйца, зелень лук и клубничное варенье. Сколько различных начинок можно приготовить из этих продуктов? При этом не надо забывать, что пироги должны быть вкусными. Вряд ли кто из вас захочет съесть пирог с начинкой из капусты с клубничным вареньем.
18. Наташа, Данила, Андрей и Маша – лучшие литераторы в классе. На школьную олимпиаду «Знатоки литературы» нужно выставить команду из двух человек. Можно ли составить 5 различных команд? Сколько различных команд, составленных из одной девочки и одного мальчика, может выставить данный класс?
19. В клетке сидят 7 мартышек. Служитель зоопарка должен дать каждой из них по два любых плода. При этом надо учесть, что капризные мартышки не любят получать одинаковые наборы. Сможет служитель угостить всех мартышек, если у него есть только бананы, яблоки и персики? Сколько еще других сортов фруктов надо иметь служителю, чтобы угостить всех мартышек?
20. В студии современного танца лучше всех танцуют четыре девочки – Аня, Ира, Оля и Яна и три мальчика – Боря, Володя и Гриша. Руководитель студии должен отправить на конкурс одну танцевальную пару, составленную из мальчика и девочки. Из скольких вариантов он должен выбирать?
21. Данила идет на день рождения к Наташе и хочет подарить два букета – один Наташе, один ее маме. Сколькими способами он может выбрать два букета, если в магазине есть букеты гвоздик, тюльпанов и сирени?
4. Анализ урока (подведение итогов, что успели сделать, что не успели (почему?), оценки за урок).
5. Домашнее задание: задается с учетом выполненных заданий на уроке из рабочей карточки.
Рабочая карточка учащегося, использующаяся на уроке, представлена в приложении 1.