Что такое дерево в информатике 9 класс

Структуры данных. Деревья

Статья познакомит вас с понятием дерева как структуры данных, пояснит в каких случаях и для чего можно их применять:

1 Что такое деревья (в программировании)?

Математическое определение дерева — «граф без петель и циклов» вряд-ли пояснит рядовому человеку какие выгоды можно извлечь из такой структуры данных.

В некоторых книгах, посвященным разработке алгоритмов, деревья определяются рекурсивно. Дерево является либо пустым, либо состоит из узла (корня), являющегося родительским узлом для некоторого количества деревьев (это количество определяет арность дерева) [1, 2].

Рабочее определение (в рамках этой статьи): дерево — это способ организации данных в виде иерархической структуры.

Когда применяются древовидные структуры:

Двоичный поиск [3] выполняется над отсортированным массивом. На каждом шаге искомый элемент сравнивается со значением, находящимся посередине массива. В зависимости от результатов сравнения — либо левая, либо правая части могут быть «отброшены».

Иерархия — способ упорядочивания объектов, соответственно применять ее можно для ускорения поиска. Именно этому посвящена остальная часть статьи.

2 Деревья и другие структуры данных

Итак, у нас есть много данных — возможно это информация о температуре за несколько лет, а может быть — данные о фирмах в вашем городе. Как хранить их внутри вашего приложения? — Правильный ответ зависит от того, как именно вы будете пользоваться этими данными.

В таблице приведены асимптотические оценки часто используемых операций над некоторыми структурами данных. На случай если вы еще не освоили асимптотический анализ, в таблице показано примерное значение количества действий, необходимых для выполнения операции над контейнером из 10 тысяч элементов.

удаление элемента по указателю (итератору)

поиск элемента с заданным значением

вставка элемента (значения)

(вернет i-тый по значению элемент)

Особенностью массивов является хранение данных в непрерывной области памяти. За счет этого обеспечивается максимальная эффективность операции произвольного доступа, однако:

При поиске значения в массиве мы в худшем случае переберем все элементы, то есть выполним O(n) операций. Однако, если массив упорядочен — мы можем применить двоичный поиск, который значительно эффективнее.

Деревья поиска, как и связные списки состоят из узлов, связанных указателями. Однако узлы эти упорядочены определенным образом — за счет этого увеличивается эффективность поиска, но осложняется операция вставки элемента. Эта структура данных, в ряде случаев,может иметь преимущества над массивами и связными списками — посмотрим за счет чего это обеспечивается…

3 Деревья поиска

Двоичное дерево состоит из узлов, каждый из которых хранит свое значение, а также две ссылки — на правое и левое поддерево. Если справа или слева нет узлов — соответствующая ссылка равна нулю (в С++ — нулевой указатель). Дерево представляется корнем (ссылкой на самый верхний узел).

Особенность дерева поиска заключается в алгоритме построения — значения вершин левого поддерева должны всегда оказываться меньше или равны значению корневого узла, а правого – больше.

При обходе такого дерева, начиная с левого поддерева, значения будут просмотрены в порядке неубывания, начиная с правого – невозрастания, т.е. дерево поиска хранит отсортированные данные:

Операция вставки выполняет добавление листа в дерево, то справа и слева от нового узла будет пусто ( null ). При вставке мы выполняем поиск подходящей свободной позиции, с учетом требования «значения вершин левого поддерева должны всегда оказываться меньше или равны значению корневого узла, а правого – больше». Алгоритм вставки значения E в дерево может выглядеть так:

Пример использования такого алгоритма приведен в таблице:

Этот пример иллюстрирует основную проблему описанного тут алгоритма вставки узлов — если подать ему на вход упорядоченные данные — то дерево «вытянется» в обыкновенный двусвязный список. В частности, для выполнения поиска в таком «дереве» из N элементов нам придется перейти по укзателям N раз.

Удаление элемента из дерева поиска, несколько запутаннее, поэтому алгоритм тут не приведен, зато приведены поясняющие иллюстрации:

4 Kd-деревья

Во многих программах появляется необходимость хранения и эффективной обработки объектов на плоскости. Это не только картографические приложения, но и все двумерные игры. Задумывались ли вы о том, как эту задачу решают игровые движки?

Мы уже разобрались с тем, что для эффективной реализации поиска объекты нужно хранить упорядоченными. Однако, как хранить точки? — ведь у них есть две (или три) координаты, а сортировка по одной из них не обеспечит приемлемую скорость поиска. Именно эти проблемы решают Kd-деревья.

Общая идея kd-деревьев заключается в разделении плоскости, содержащей объекты на части (прямоугольные области) таким образом, что в каждой области содержится один объект. При этом, между областями можно выстроить иерархические зависимости, за счет которых можно существенно повысить эффективность поиска. Существуют различные типы kd-деревьев, отличающиеся выбором секущей плоскости.

Задача: есть множество точек, находящихся на плоскости, нужно выстроить объекты в иерархическую структуру, исходя из их координат для обеспечения эффективного поиска. Описанные ниже подходы можно обобщить до более сложных геометрических объектов (не точек) и пространств больших размерностей.

Первый вариант решения:

С такой структурой данных, алгоритм вывода всех точек, входящих в Прямоугольник может выглядеть так:

Цветом на приведенной выше схеме обозначена область поиска. Она не пересекается с областью B (расположенной левее А ). Даже если бы в этой области были миллионы точек — мы «отсекли» бы их за одну итерацию алгоритма — то есть мы получили полноценный двоичный поиск на плоскости. Визуализация алгоритма:

При перемещении объектов может возникать необходимость перестроения дерева — если объект переместился из одной области «родительского» объекта в другую.

Описанный подход называется Kd-деревья с циклическим проходом по измерениям. Возможны и другие варианты выбора секущей плоскости — например каждый узел квадрадерева делит свою часть плоскости на 4 части (левая верхняя, левая нижняя, правая верхняя, права нижняя). Если в какой-то части оказывается более 1 объекта — то она делится дальше. Октадеревья адаптируют эту идею к трехмерному пространству.

Источник

Дерево

Дерево – структура данных, представляющая собой древовидную структуру в виде набора связанных узлов.

Способ представления бинарного дерева:

Корень дерева расположен на уровне с минимальным значением.

Если элемент не имеет потомков, он называется листом или терминальным узлом дерева.

Остальные элементы – внутренние узлы (узлы ветвления).

Бинарное дерево применяется в тех случаях, когда в каждой точке вычислительного процесса должно быть принято одно из двух возможных решений.

Имеется много задач, которые можно выполнять на дереве.

Распространенная задача — выполнение заданной операции p с каждым элементом дерева. Здесь p рассматривается как параметр более общей задачи посещения всех узлов или задачи обхода дерева.

Если рассматривать задачу как единый последовательный процесс, то отдельные узлы посещаются в определенном порядке и могут считаться расположенными линейно.

Способы обхода дерева

Пусть имеем дерево, где A — корень, B и C — левое и правое поддеревья.

Существует три способа обхода дерева:

Реализация дерева

Узел дерева можно описать как структуру:

При этом обход дерева в префиксной форме будет иметь вид

Обход дерева в инфиксной форме будет иметь вид

Обход дерева в постфиксной форме будет иметь вид

Бинарное (двоичное) дерево поиска – это бинарное дерево, для которого выполняются следующие дополнительные условия (свойства дерева поиска):

Данные в каждом узле должны обладать ключами, на которых определена операция сравнения меньше.

Как правило, информация, представляющая каждый узел, является записью, а не единственным полем данных.

Для составления бинарного дерева поиска рассмотрим функцию добавления узла в дерево.

Добавление узлов в дерево

Удаление поддерева

Пример Написать программу, подсчитывающую частоту встречаемости слов входного потока.

Поскольку список слов заранее не известен, мы не можем предварительно упорядочить его. Неразумно пользоваться линейным поиском каждого полученного слова, чтобы определять, встречалось оно ранее или нет, т.к. в этом случае программа работает слишком медленно.

Один из способов — постоянно поддерживать упорядоченность уже полученных слов, помещая каждое новое слово в такое место, чтобы не нарушалась имеющаяся упорядоченность. Воспользуемся бинарным деревом.

В дереве каждый узел содержит:

Рассмотрим выполнение программы на примере фразы

now is the time for all good men to come to the aid of their party

При этом дерево будет иметь следующий вид

Результат выполнения

Источник

Какой граф называется деревом? Что такое дерево в информатике?

Содержание:

Граф-дерево является очень распространенным видом графов в информатике. Они нужны для хранения какой-либо информации в нелинейной структуре в иерархическом порядке.

Граф — это структура, состоящая из множества вершин, соединенных ребрами. Все в своей жизни видели транспортные схемы (передвижение автобусов или метро). Если эти схемы смоделировать в компьютере, то остановки и станции — это будут вершины графа, а маршрут транспорта между остановками/станциями — ребра графа.

В зависимости от того, каким образом расположены вершины, какое отношение между ними и каким способом они соединяются между собой ребрами, различают различные виды графов. Граф-дерево — это всего лишь один из множества видов графов.

Граф-дерево

Самое главное, все имена вы соединяли линиями зависимости между собой. Например, свое имя соединили с именами братьев и сестер и с именами своих родителей. Имена ваших родителей вы соединили с именами их братьев и сестер и с их родителями и т. д.

В информатике, граф-дерево выглядит точно так же, как и ваше генеалогическое дерево, только вместо имен — вершины, а вместо линий, связывающих имена — ребра.

Охарактеризовать граф-дерево в информатике можно так — это связный граф, где между двумя вершинам есть единственный связный путь. Вернемся к нашему дереву. Ваше имя будет связано линиями только с вашими родителями и вашими братьями/сестрами, с другими именами дерева у вас нет прямой связи. Например, с вашими дядями, тетями, бабушками и дедушками вы будете связаны только через ваших родителей, а не напрямую. А с вашей прабабушкой или вашим прадедушкой вы будете связаны только через родителей и бабушек с дедушками.

То есть граф-дерево в информатике следует строгой иерархии — одни элементы находятся «наверху» графа и будут называться «корнем дерева», другие элементы будут чуть ниже и будут называться «потомками», от «потомков» будут исходить «листья» — это те вершины, которые не имеют «потомков». Любой элемент верхнего уровня по отношению к нижнему уровню будет называться «предком».

Вернемся к нашему генеалогическому дереву. Бабушка с дедушкой (или прабабушка с прадедушкой, то есть в зависимости до какой глубины своих предков вы дойдете) будут корнем вашего граф-дерева (либо подкорнем, если у вас в корне будут прабабушка с прадедушкой). Ваши родители — это «потомки» вашего граф-дерева и бабушка с дедушкой для них будут «предками» вашего дерева. Вы будете «листьями» граф-дерева, потому что у вас пока нет своего потомства, как только у вас появятся дети, то вы станете «потомками» графа, а ваши дети «листьями». Ваши родители для вас будут «предками» графа.

Источник

Все что нужно знать о древовидных структурах данных

Jul 1, 2018 · 14 min read

Деревья прекрасны. Вот рисунок, который я сделал ребенком

Когда вы впервые учитесь кодировать, общепринято изучать массивы в качестве «основной структуры данных».

В конце концов, вы также изучаете хэш-таблицы. Для получения степени по «Компьютерным наукам» (Computer Science) вам придется походить на занятия по структурам данных, на которых вы узнаете о связанных списках, очередях и стеках. Эти структуры данных называются «линейными», поскольку они имеют логические начало и завершение.

Однако в самом начале и зучения деревьев и графов мы можем оказаться слегка сбитыми с толку. Нам привычно хранить данные линейным способом, а эти две структуры хранят данные совершенно иначе.

Данная статья поможет вам лучше понять древовидные структуры данных и устранить все недоразумения на их счет.

Из этой статьи вы узнаете:

Давайте начнем наше учебное путешествие 🙂

Определения

Когда вы только начинаете изучать программирование, обычно бывает проще понять, как строятся линейные структуры данных, чем более сложные структуры, такие как деревья и графы.

Деревья являются широко известными нелинейными структурами. Они хранят данные не линейным способом, а упорядочивают их иерархически.

Давайте вплотную займемся реальными примерами

Что я имею в виду, когда я говорю иерархически?

Представьте себе генеалогическое древо отношений между поколениями: бабушки и дедушки, родители, дети, братья и сестры и т.д. Мы обычно организуем семейные деревья иерархически.

Мое фамильное дерево

Приведенный рисунок — это мое фамильное древо. Тосико, Акикадзу, Хитоми и Такеми — мои дедушки и бабушки.

Тошиаки и Джулиана — мои родители.

ТК, Юдзи, Бруно и Кайо — дети моих родителей (я и мои братья).

Структура организации — еще один пример иерархии.

Структура компании является примером иерархии

В HTML, объектная модель документа (DOM) представляется в виде дерева.

Объектная модель документа (DOM)

Техническое определение

Дерево представляет собой набор объектов, называемых узлами. Узлы соединены ребрами. Каждый узел содержит значение или данные, и он может иметь или не иметь дочерний узел.

Первый узел дерева называется корнем. Если этот корневой узел соединен с другим узлом, тогда корень является родительским узлом, а связанный с ним узел — дочерним.

Все узлы дерева соединены линиями, называемыми ребрами. Это важная часть деревьев, потому что она управляет связью между узлами.

Листья — это последние узлы на дереве. Это узлы без потомков. Как и в реальных деревьях, здесь имеется корень, ветви и, наконец, листья.

Другими важными понятиями являются высота и глубина.

Высота дерева — это длина самого длинного пути к листу.

Глубина узла — это длина пути к его корню.

Справочник терминов

Бинарные деревья

Теперь рассмотрим особый тип деревьев, называемых бинарными или двоичными деревьями.

“В информатике бинарным (двоичным) деревом называется иерархическая структура данных, в которой каждый узел имеет не более двух потомков (детей). Как правило, первый называется родительским узлом, а дети называются левым и правым наследниками.” — Wikipedia

Рассмотрим пример бинарного дерева.

Давайте закодируем бинарное дерево

Как мы реализуем простое двоичное дерево, которое инициализирует эти три свойства?

Вот наш двоичный класс дерева.

Когда мы создаем наш узел, он не имеет потомков. Просто есть данные узла.

Давайте это проверим:

Перейдем к части вставки. Что нам нужно здесь сделать?

Мы реализуем метод вставки нового узла справа и слева.

Давайте это нарисуем 🙂

Вот программный код:

Еще раз, если текущий узел не имеет левого дочернего элемента, мы просто создаем новый узел и устанавливаем его в качестве left_child текущего узла. Или мы создаем новый узел и помещаем его вместо текущего левого потомка. Назначим этот левый дочерний узел в качестве левого дочернего элемента нового узла.

И мы делаем то же самое, чтобы вставить правый дочерний узел.

Но не полностью. Осталось протестировать.

Давайте построим следующее дерево:

Подытоживая изображенное дерево, заметим:

Таким образом, вот код для нашего дерева следующий:

Теперь нам нужно подумать об обходе дерева.

У нас есть два варианта: поиск в глубину (DFS) и поиск по ширине (BFS).

• Поиск в глубину (Depth-first search, DFS) — один из методов обхода дерева. Стратегия поиска в глубину, как и следует из названия, состоит в том, чтобы идти «вглубь» дерева, насколько это возможно. Алгоритм поиска описывается рекурсивно: перебираем все исходящие из рассматриваемой вершины рёбра. Если ребро ведёт в вершину, которая не была рассмотрена ранее, то запускаем алгоритм от этой нерассмотренной вершины, а после возвращаемся и продолжаем перебирать рёбра. Возврат происходит в том случае, если в рассматриваемой вершине не осталось рёбер, которые ведут в не рассмотренную вершину. Если после завершения алгоритма не все вершины были рассмотрены, то необходимо запустить алгоритм от одной из не рассмотренных вершин.

• Поиск в ширину (breadth-first search, BFS) — метод обхода дерева и поиска пути. Поиск в ширину является одним из неинформированных алгоритмов поиска. Поиск в ширину работает путём последовательного просмотра отдельных уровней дерева, начиная с узла-источника. Рассмотрим все рёбра, выходящие из узла. Если очередной узел является целевым узлом, то поиск завершается; в противном случае узел добавляется в очередь. После того, как будут проверены все рёбра, выходящие из узла, из очереди извлекается следующий узел, и процесс повторяется.

Давайте подробно рассмотрим каждый из алгоритмов обхода.

Поиск в глубину (DFS)

DFS исследует все возможные пути вплоть до некоторого листа дерева, возвращается и исследует другой путь (осуществляя, таким образом, поиск с возвратом). Давайте посмотрим на пример с этим типом обхода.

Результатом этого алгоритма будет: 1–2–3–4–5–6–7.

Давайте разъясним это подробно.

Проход в глубь дерева, а затем возврат к исходной точке называется алгоритмом DFS.

После знакомства с этим алгоритмом обхода, рассмотрим различные типы DFS-алгоритма: предварительный обход (pre-order), симметричный обход (in-order) и обход в обратном порядке (post-order).

Предварительный обход

Именно это мы и делали в вышеприведенном примере.

1. Записать значение узла.

2. Перейти к левому потомку и записать его. Это выполняется тогда и только тогда, когда имеется левый потомок.

3. Перейти к правому потомку и записать его. Это выполняется тогда и только тогда, когда имеется правый потомок.

Источник

Урок 12
§16. Списки и деревья

Содержание урока

Что такое дерево?

Что такое дерево?

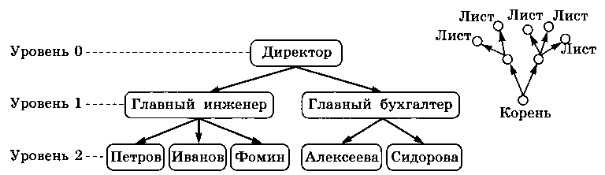
Предположим, в некоторой фирме есть директор, ему подчиняются главный инженер и главный бухгалтер, у каждого из них есть свои подчинённые. Если мы захотим нарисовать схему управления этой фирмы, она получится многоуровневой (рис. 3.8).

Такая структура, в которой одни элементы «подчиняются» другим, называется иерархической. В информатике её называют деревом.

Дело в том, что, если перевернуть эту схему вверх нотами, она становится похожа на дерево.

Дерево — это структура данных, которая служит моделью многоуровневой структуры (иерархии).

Несколько деревьев образуют лес.

Используя дополнительные источники, выясните, от какого иностранного слова произошло слово «иерархия».

Следующая страница Из чего состоит дерево?

Cкачать материалы урока

Источник