Что такое дельта в матрице
Решение матриц методы решений и примеров для чайников, формулы вычислений и действий с матрицами
В высшей математике существует понятие матрицы системы чисел. С комбинацией элементов, заключённых в таблице, выполняют различные операции. Прежде чем переходить к решению матриц сложными методами, следует ознакомиться с понятием этого выражения и простейшими логическими операциями над ним.
Понятие выражения
Определение гласит, что матрица — это прямоугольная таблица с заключёнными в ней числами. Её название обозначается латинскими прописными буквами (А, В). Таблицы бывают разной размерности — прямоугольной, квадратной, а также в виде строк и столбцов.
От количества строк и столбцов будет зависеть величина таблицы. Матрица размера m*n означает, что в таблице содержится m строк и n столбцов. Допустим, первая строка включает элементы а11, а12, а13, вторая — а21, а22, а23. Тогда элементы, где i = j (а11, а22) образовывают диагональ и называются диагональными.
Различают комплексные матрицы, у которых хотя бы один элемент равен комплексному числу, и действительные, когда все её элементы являются действительными числами. В математике комплексные числа представлены в виде a+b*i, где:
На приведенном примере показаны варианты.
Простейшие действия с матрицами могут быть разными. К их числу относятся:
Сложение и вычитание
Действия по сложению возможны только тогда, когда матрицы одинакового порядка равны между собой. В итоге получится новое матричное выражение такой же размерности. Сложение и вычитание выполняются по общей схеме — над соответствующими элементами таблиц проводят необходимые операции. Например, нужно сложить две матрицы А и В размерности 2*2.
Каждый элемент первой строки складывается по порядку с показателями верхней строчки второй матрицы. По аналогии производится вычитание, только вместо плюса ставится минус.
Умножение на число
Любую таблицу чисел можно умножить на число. Тогда каждый её элемент перемножается с этим показателем. К примеру, умножим матричное выражение на 2:
Операция перемножения
Матрицы подлежат перемножению одна на другую, когда количество столбцов первой таблицы равно числу строк второй. Каждый элемент Aij будет равняться сумме произведений элементов i-строки первой таблицы, перемноженных на числа в j-столбце второй. Способ произведения наглядно представлен на примере.
Возведение в степень
Формулу возведения в степень применяют только для квадратных матричных выражений. При этом степень должна быть натуральной. Формула возведения следующая:
Иначе, чтобы выполнить операцию возведения таблицы чисел в степень n, требуется умножить её на себя саму n раз. Для операции возведения в степень удобно применять свойство в соответствии с формулой:
Решение представлено на примере. 1 этап: необходимо возвести в степень, где n = 2.
2 этап: сначала возводят в степень n =2. Согласно формуле перемножают таблицу чисел саму на себя n = 2 раз.
3 этап: в итоге получаем:
Расчёт определителя
В линейной алгебре существует понятие определителя или детерминанта. Это число, которое ставят в соответствие каждой квадратной матрице, вычисленное из её элементов по специальной формуле. Определитель или модуль используется для решения большинства задач. Детерминант самой простой матрицы определяется с помощью вычитания перемноженных элементов из побочной диагонали и главной.
Определителем матрицы А n-энного порядка называется число, которое получают из алгебраической суммы n! слагаемых, попадающих под определённые критерии. Эти слагаемые являются произведением n-элементов, взятых единично из всех столбов и строк.
Произведения могут отличаться друг от друга составом элементов. Со знаком плюс будут включаться в сумму числа, если их индексы составляют чётную подстановку, в противоположном случае их значение меняется на минус. Определитель обозначается символом det A. Круглые скобки матричной таблицы, обрамляющие её элементы, заменяются на квадратные. Формула определителя:
Определитель первого порядка, состоящий из одного элемента, равен самому этому элементу. Детерминант матричной таблицы размером 2*2 второго порядка вычисляется путём перемножения её элементов, расположенных на главной диагонали, и вычитания из них произведения элементов, находящихся в побочной диагонали. Наглядный пример:
Для матрицы также можно найти дискриминант многочлена, отвечающий формуле:
Когда у многочлена имеются кратные корни, тогда дискриминант равен нулю.
Обратная матрица
Прежде чем переходить к понятию обратного выражения матрицы, следует рассмотреть алгоритм её транспонирования. Во время операции строки и столбцы переставляются местами. На рисунке представлен метод решения:
По аналогии обратная матрица сходна с обратными числами. Например, противоположной цифре 5 будет дробь 1/5 = 5 (-1) степени. Произведение этих чисел равно 1, выглядит оно так: 5*5 (-1) = 1. Умножение обычной матричной таблицы на обратную даст в итоге единичную: А* А (-1) = Е. Это аналог числовой единицы.
Но для начала нужно понять алгоритм вычисления обратной матрицы. Для этого находят её определитель. Разработано два метода решения: с помощью элементарных преобразований или алгебраических дополнений.
Более простой способ решения — путём алгебраических дополнений. Рассмотрим матричную таблицу А, обратная ей А (-1) степени находится по формуле:
Матрица обратного вида возможна только для квадратного размера таблиц 2*2, 3*3 и т. д. Обозначается она надстроенным индексом (-1). Задачу легче рассмотреть на более простом примере, когда размер таблицы равен 2*2. На первом этапе выполняют действия:
2 этап: рассчитывают матрицу миноров, которая имеет те же значения, что и первоначальная. Под минором k-того порядка понимается определитель квадратной матрицы порядка k*k, составленный из её элементов, которые располагаются в выбранных k- столбцах и k-строках.
При этом расположение элементов таблицы не меняется. Чтобы найти минор верхнего левого числа, вычёркивают строчку и столбец, в которых прописан этот элемент. Оставшееся число и будет являться минором. На выходе должна получиться таблица:
3 этап: находят алгебраические дополнения.
4 этап: определяют транспонированную матрицу.
Проверка решения: чтобы удостовериться, что обратная таблица чисел найдена верно, следует выполнить проверочную операцию.
В рассматриваемом примере получается единичная матрица, когда на главной диагонали находятся единицы, при этом другие элементы равняются нулю. Это говорит о том, что решение было найдено правильно.
Нахождение собственных векторов
Определение собственного вектора и значений матричного выражения легче понять на примере. Для этого задают матричную таблицу чисел и ненулевой вектор Х, называемый собственным для А. Пример выражения:
Согласно теореме собственными числами матричного выражения будут корни характеристического уравнения:
Из однородной системы уравнений можно определить координаты собственного вектора Х, который соответствует значению лямбда.
Метод Гаусса
Методом Гаусса называют способ преобразования системы уравнений линейного вида к упрощённой форме для дальнейшего облегчённого решения. Операции упрощения уравнений выполняют с помощью эквивалентных преобразований. К таким относят:
Чтобы понять механизм решения, следует рассмотреть линейную систему уравнений.
Следует переписать эту систему в матричный вид:
А будет являться таблицей коэффициентов системы, b — это правая часть ограничений, а Х — вектор переменных координат, который требуется найти. Для решения используют ранг матрицы. Под ним понимают наивысший порядок минора, который отличается от 0.
В этом примере rang (A) = p. Способ эквивалентных преобразований не изменяет ранг таблицы коэффициентов.
Метод Гаусса предназначен для приведения матричной таблицы коэффициентов А к ступенчатому или диагональному виду. Расширенная система выглядит так:
Обращают внимание на последние строки.
В этом случае система уравнений имеет решение, но когда хотя бы одно из этих чисел отличается от нуля, она несовместима. Таким образом, система совместима, если ранг таблицы А равен расширенному рангу В (А|b).
Если rang А=rang (A|b), то существует множество решений, где n-p — многообразие. Из этого следует n-p неизвестных Хр+1,…Xn выбираются произвольно. Неизвестные X1, X2,…Xp вычисляют следующим образом: из последнего уравнения выражают Хр через остальные переменные, вставляя в предыдущие выражения. Затем из предпоследнего уравнения получают Хр-1 через прочие переменные и подставляют их в предыдущие выражения. Процедуру повторяют.
Найти быстро ответ и проверить себя позволяет онлайн-калькулятор. Решение матрицы методом Гаусса с помощью такого расчёта показывает подробные этапы операций. Для нахождения достаточно указать количество переменных и уравнений, отметить в полях значения чисел и нажать кнопку «Вычислить».
Способ Крамера
Метод Крамера используют для решения квадратной системы уравнений, представленной в линейном виде, где определитель основной матрицы не равен нулю. Считается, что система обладает единственным решением. Например, задана система линейных уравнений:
Её необходимо заменить равноценным матричным уравнением.
Второй столбец вычисляют, а первый уже задан. Есть предположение, что определитель матрицы отличен от нуля. Из этого можно сделать выводы, что существует обратная матрица. Перемножив эквивалентное матричное уравнение на обратного формата матрицу, получим выражение:
В итоге получают выражения:
Из представленных уравнений выделяют формулы Крамера:
Метод Крамера не представляет сложности. Он может быть описан следующим алгоритмом:
Проверить решение матрицы методом Крамера онлайн позволяет калькулятор автоматического расчёта. Для получения быстрого ответа в представленные поля подставляют переменные числа и их количество. Дополнительно может потребоваться указание вычислительного метода разложения по строке или столбу. Другой вариант заключается в приведении к треугольному виду.
Указывается также представление чисел в виде целого числа, обыкновенной или десятичной дроби. После введения всех предусмотренных параметров и нажатия кнопки «Вычислить» получают готовое решение.
Определитель матрицы и его свойства
Помню, класса до 8-го мне не нравилась алгебра. Вообще не нравилась. Бесила она меня. Потому что я там ничего не понимал.
А затем всё изменилось, потому что я просёк одну фишку:
В математике вообще (и алгебре в частности) всё строится на грамотной и последовательной системе определений. Знаешь определения, понимаешь их суть — разобраться в остальном не составит труда.
Вот так и с темой сегодняшнего урока. Мы детально рассмотрим несколько смежных вопросов и определений, благодаря чему вы раз и навсегда разберётесь и с матрицами, и с определителями, и со всеми их свойствами.
Определители — центральное понятие в алгебре матриц. Подобно формулам сокращённого умножения, они будут преследовать вас на протяжении всего курса высшей математики. Поэтому читаем, смотрим и разбираемся досконально.:)
И начнём мы с самого сокровенного — а что такое матрица? И как правильно с ней работать.
Правильная расстановка индексов в матрице
Матрица — это просто таблица, заполненная числами. Нео тут ни при чём.
\[A=\left[ m\times n \right]\]
Какой индекс за что отвечает? Сначала идёт номер строки, затем — столбца? Или наоборот?
При чтении лекций и учебников ответ будет казаться очевидным. Но когда на экзамене перед вами — только листик с задачей, можно переволноваться и внезапно запутаться.
Поэтому давайте разберёмся с этим вопросом раз и навсегда. Для начала вспомним обычную систему координат из школьного курса математики:
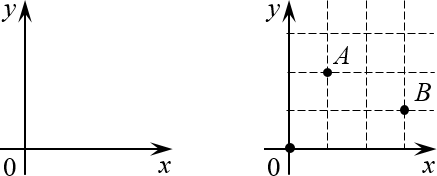
А теперь давайте возьмём эту конструкцию и поставим её рядом с матрицей так, чтобы начало координат находилось в левом верхнем углу. Почему именно там? Да потому что открывая книгу, мы начинаем читать именно с левого верхнего угла страницы — запомнить это легче лёгкого.
Но куда направить оси? Мы направим их так, чтобы вся наша виртуальная «страница» была охвачена этими осями. Правда, для этого придётся повернуть нашу систему координат. Единственно возможный вариант такого расположения:
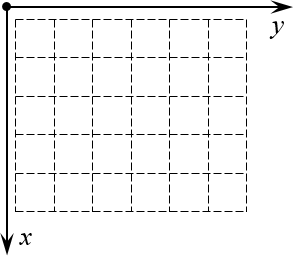
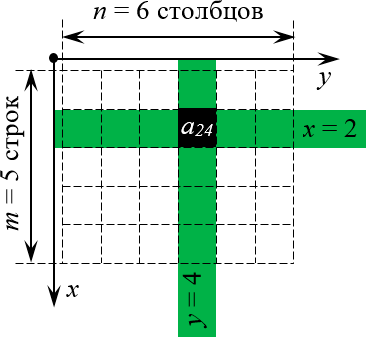
Просто всмотритесь в эту картинку внимательно. Поиграйтесь с координатами (особенно когда будете работать с настоящими матрицами и определителями) — и очень скоро поймёте, что даже в самых сложных теоремах и определениях вы прекрасно понимаете, о чём идёт речь.
Разобрались? Что ж, переходим к первому шагу просветления — геометрическому определению определителя.:)
Геометрическое определение
Ну и что это за характеристика? Что он означает? Всё просто:
Например, определитель матрицы размера 2×2 — это просто площадь параллелограмма, а для матрицы 3×3 это уже объём 3-мерного параллелепипеда — того самого, который так бесит всех старшеклассников на уроках стереометрии.
На первый взгляд это определение может показаться совершенно неадекватным. Но давайте не будем спешить с выводами — глянем на примеры. На самом деле всё элементарно, Ватсон:
Задача. Найдите определители матриц:
Решение. Первые два определителя имеют размер 2×2. Значит, это просто площади параллелограммов. Начертим их и посчитаем площадь.
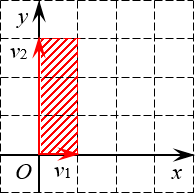
Очевидно, это не просто параллелограмм, а вполне себе прямоугольник. Его площадь равна
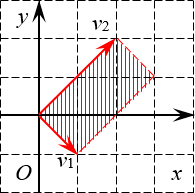
Стороны этого прямоугольника (по сути — длины векторов) легко считаются по теореме Пифагора:
Осталось разобраться с последним определителем — там уже матрица 3×3. Придётся вспоминать стереометрию:
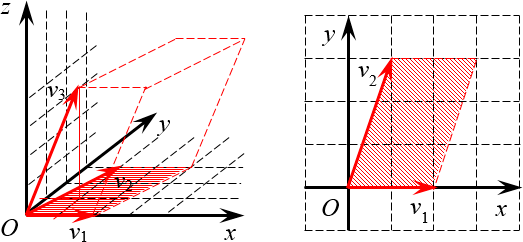
Выглядит мозговыносяще, но по факту достаточно вспомнить формулу объёма параллелепипеда:
Площадь параллелограмма (мы начертили его отдельно) тоже считается легко:
Вот и всё! Записываем ответы.
Небольшое замечание по поводу системы обозначений. Кому-то наверняка не понравится, что я игнорирую «стрелочки» над векторами. Якобы так можно спутать вектор с точкой или ещё с чем.
Но давайте серьёзно: мы с вами уже взрослые мальчики и девочки, поэтому из контекста прекрасно понимаем, когда речь идёт о векторе, а когда — о точке. Стрелки лишь засоряют повествование, и без того под завязку напичканное математическими формулами.
И ещё. В принципе, ничто не мешает рассмотреть и определитель матрицы 1×1 — такая матрица представляет собой просто одну клетку, а число, записанное в этой клетке, и будет определителем. Но тут есть важное замечание:
В отличие от классического объёма, определитель даст нам так называемый «ориентированный объём», т.е. объём с учётом последовательности рассмотрения векторов-строк.
И если вы хотите получить объём в классическом смысле этого слова, придётся взять модуль определителя, но сейчас не стоит париться об этом — всё равно через несколько секунд мы научимся считать любой определитель с любыми знаками, размерами и т.д.:)
Алгебраическое определение
При всей красоте и наглядности геометрического подхода у него есть серьёзный недостаток: он ничего не говорит нам о том, как этот самый определитель считать.
Поэтому сейчас мы разберём альтернативное определение — алгебраическое. Для этого нам потребуется краткая теоретическая подготовка, зато на выходе мы получим инструмент, позволяющий считать в матрицах что и как угодно.
Правда, там появится новая проблема. но обо всём по порядку.
Перестановки и инверсии
Теперь (чисто по приколу) поменяем парочку чисел местами. Можно поменять соседние:
А можно — не особо соседние:
И знаете, что? А ничего! В алгебре эта хрень называется перестановкой. И у неё есть куча свойств.
Далее для простоты изложения будем работать с перестановками длины 5 — они уже достаточно серьёзны для наблюдения всяких подозрительных эффектов, но ещё не настолько суровы для неокрепшего мозга, как перестановки длины 6 и более. Вот примеры таких перестановок:
\[n!=5!=1\cdot 2\cdot 3\cdot 4\cdot 5=120\]
Одной из ключевых характеристик всякой перестановки является количество инверсий в ней.
\[\left( 4;3 \right);\left( 4;2 \right);\left( 5;3 \right);\left( 5;2 \right);\left( 3;2 \right).\]
Что такое определитель
Принципиальным моментом при выборе множителей для каждого слагаемого в определителе является тот факт, что никакие два множителя не стоят в одной строчке или в одном столбце.
\[j=p\left( i \right),\quad i=1,2. n\]
От перестановки множителей произведение чисел не меняется.
Вот только не надо приплетать это правило к умножению матриц — в отличие от умножения чисел, оно не коммутативно. Но это я отвлёкся.:)
Матрица 2×2
Вообще-то можно рассмотреть и матрицу 1×1 — это будет одна клетка, и её определитель, как нетрудно догадаться, равен числу, записанному в этой клетке. Ничего интересного.
Поэтому давайте рассмотрим квадратную матрицу размером 2×2:
Рассмотрим пару примеров:
Решение. Всё считается в одну строчку. Первая матрица:
\[5\cdot 9-8\cdot 6=45-48=-3\]
\[7\cdot 1-14\cdot 12=7-168=-161\]
Впрочем, это было слишком просто. Давайте рассмотрим матрицы 3×3 — там уже интересно.
Матрица 3×3
Теперь рассмотрим квадратную матрицу размера 3×3:
\[\begin _<1>>=\left( 1;2;3 \right)\Rightarrow N\left( < _<1>> \right)=N\left( 1;2;3 \right)=0; \\ & < _<2>>=\left( 1;3;2 \right)\Rightarrow N\left( < _<2>> \right)=N\left( 1;3;2 \right)=1; \\ & < _<3>>=\left( 2;1;3 \right)\Rightarrow N\left( < _<3>> \right)=N\left( 2;1;3 \right)=1; \\ & < _<4>>=\left( 2;3;1 \right)\Rightarrow N\left( < _<4>> \right)=N\left( 2;3;1 \right)=2; \\ & < _<5>>=\left( 3;1;2 \right)\Rightarrow N\left( < _<5>> \right)=N\left( 3;1;2 \right)=2; \\ & < _<6>>=\left( 3;2;1 \right)\Rightarrow N\left( < _<6>> \right)=N\left( 3;2;1 \right)=3. \\\end Вот только не надо сейчас садиться и яростно зубрить все эти индексы! Вместо непонятных цифр лучше запомните следующее мнемоническое правило: . Для нахождения определителя матрицы 3×3 нужно сложить три произведения элементов, стоящих на главной диагонали и в вершинах равнобедренных треугольников со стороной, параллельной этой диагонали, а затем вычесть такие же три произведения, но на побочной диагонали. Схематически это выглядит так: Именно эти треугольники (или пентаграммы — кому как больше нравится) любят рисовать во всяких учебниках и методичках по алгебре. Впрочем, не будем о грустном. Давайте лучше посчитаем один такой определитель — для разминки перед настоящей жестью.:) \[\left| \begin Решение. Работаем по правилу треугольников. Сначала посчитаем три слагаемых, составленных из элементов на главной диагонали и параллельно ей: \[\begin Теперь разбираемся с побочной диагональю: \[\begin Осталось лишь вычесть из первого числа второе — и мы получим ответ: Тем не менее, определители матриц 3×3 — это ещё не вершина мастерства. Самое интересное ждёт нас дальше.:) Уже для матриц 4×4 считать определители напролом (т.е. через перестановки) становится как-то не оч. Про 5×5 и более вообще молчу. Поэтому к делу подключаются некоторые свойства определителя, но для их понимания нужна небольшая теоретическая подготовка. Есть и другое определение. Возможно, кому-то оно больше придётся по душе: Как говорил мой кот, иногда лучше Выбирая строку 1 и столбец 2, получаем минор первого порядка: Выбирая строки 2, 3 и столбцы 3, 4, получаем минор второго порядка: А если выбрать все три строки, а также столбцы 1, 2, 4, будет минор третьего порядка: \[< Считать этот определитель мне уже в лом. Но он равен 53.:) Читателю не составит труда найти и другие миноры порядков 1, 2 или 3. Поэтому идём дальше. «Ну ok, и что дают нам эти Уточним один момент: дополнительный минор — это не просто «кусок матрицы», а определитель этого куска. Дополнительные миноры редко используются сами по себе. Они являются частью более сложной конструкции — алгебраического дополнения. Сложно? На первый взгляд — да. Но это не точно. Потому что на самом деле всё легко. Рассмотрим пример: \[A=\left[ \begin Выберем минор второго порядка Капитан Очевидность как бы намекает нам, что при составлении этого минора были задействованы строки 1 и 4, а также столбцы 3 и 4. Вычёркиваем их — получим дополнительный минор: Вот и всё! По сути, всё различие между дополнительным минором и алгебраическим дополнением — только в минусе спереди, да и то не всегда. Наша задача сейчас — научиться быстро считать алгебраические дополнения, потому что они являются составной частью «Теоремы, Которую Нельзя Называть». Но мы всё же назовём. Встречайте: И вот мы пришли к тому, зачем, собственно, все эти миноры и алгебраические дополнения были нужны. Мы не будем её доказывать, хоть это и не представляет особой трудности — все выкладки сводятся к старым-добрым перестановкам и чётности/ нечётности инверсий. Тем не менее, доказательство будет представлено в отдельном параграфе, а сегодня у нас сугубо практический урок. Поэтому переходим к частному случаю этой теоремы, когда миноры представляют собой отдельные клетки матрицы. То, о чём сейчас пойдёт речь — как раз и есть основной инструмент работы с определителями, ради которого затевались вся эта дичь с перестановками, минорами и алгебраическими дополнениями. Читайте и наслаждайтесь: Это и есть формула разложения определителя по строке. Но то же верно и для столбцов. Из этого следствия можно сразу сформулировать несколько выводов: Последний факт особенно важен. Например, вместо зверского определителя 4×4 теперь достаточно будет посчитать несколько определителей 3×3 — с ними мы уж как-нибудь справимся.:) Что ж, попробуем посчитать одну такую задачку? \[\left| \begin Решение. Разложим этот определитель по первой строке: Задача. Найдите определитель: \[\left| \begin Решение. Для разнообразия давайте в этот раз работать со столбцами. Например, в последнем столбце присутствуют сразу два нуля — очевидно, это значительно сократит вычисления. Сейчас увидите почему. Итак, раскладываем определитель по четвёртому столбцу: И тут — о, чудо! — два слагаемых сразу улетают коту под хвост, поскольку в них есть множитель «0». Остаётся ещё два определителя 3×3, с которыми мы легко разберёмся: Возвращаемся к исходнику и находим ответ: Ну вот и всё. И никаких 4! = 24 слагаемых считать не пришлось.:) В последней задаче мы видели, как наличие нулей в строках (столбцах) матрицы резко упрощает разложение определителя и вообще все вычисления. Возникает естественный вопрос: а нельзя ли сделать так, чтобы эти нули появились даже в той матрице, где их изначально не было? Ответ однозначен: можно. И здесь нам на помощь приходят свойства определителя: Особую ценность представляет третье свойство: мы можем вычитать из одной строки (столбца) другую до тех пор, пока в нужных местах не появятся нули. Чаще всего расчёты сводится к тому, чтобы «обнулить» весь столбец везде, кроме одного элемента, а затем разложить определитель по этому столбцу, получив матрицу размером на 1 меньше. Давайте посмотрим, как это работает на практике: \[\left| \begin Решение. Нулей тут как бы вообще не наблюдается, поэтому можно «долбить» по любой строке или столбцу — объём вычислений будет примерно одинаковым. Давайте не будем мелочиться и «обнулим» первый столбец: в нём уже есть клетка с единицей, поэтому просто возьмём первую строчку и вычтем её 4 раза из второй, 3 раза из третьей и 2 раза из последней. В результате мы получим новую матрицу, но её определитель будет тем же: Теперь с невозмутимостью Пятачка раскладываем этот определитель по первому столбцу: Понятно, что «выживет» только первое слагаемое — в остальных я даже определители не выписывал, поскольку они всё равно умножаются на ноль. Коэффициент перед определителем равен единице, т.е. его можно не записывать. Зато можно вынести «минусы» из всех трёх строк определителя. По сути, мы трижды вынесли множитель (−1): Получили мелкий определитель 3×3, который уже можно посчитать по правилу треугольников. Но мы попробуем разложить и его по первому столбцу — благо в последней строчке гордо стоит единица: Можно, конечно, ещё поприкалываться и разложить матрицу 2×2 по строке (столбцу), но мы же с вами адекватны, поэтому просто посчитаем ответ: Вот так и разбиваются мечты. Всего-то −160 в ответе.:) Парочка замечаний перед тем, как мы перейдём к последней задаче: Идём дальше. Последняя задача в сегодняшнем уроке. \[\left| \begin Решение. Ну, тут первая строка прямо-таки напрашивается на «обнуление». Берём первый столбец и вычитаем ровно один раз из всех остальных: \[\begin Раскладываем по первой строке, а затем выносим общие множители из оставшихся строк: \[\cdot \left| \begin Снова наблюдаем «красивые» числа, но уже в первом столбце — раскладываем определитель по нему: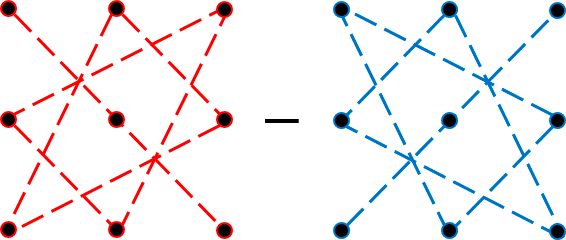
Общая схема вычисления определителей
Что такое минор матрицы
один раз навернуться с 11-го этажа есть корм, чем мяукать, сидя на балконе.Алгебраические дополнения
миньоны миноры?» — наверняка спросите вы. Сами по себе — ничего. Но в квадратных матрицах у каждого минора появляется «компаньон» — дополнительный минор, а также алгебраическое дополнение. И вместе эти два ушлёпка позволят нам щёлкать определители как орешки.Теорема Лапласа
Разложение определителя по строке и столбцу
Основные свойства определителя






































