Что такое дельта икс
Решение производной для чайников: определение, как найти, примеры решений
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Геометрический и физический смысл производной
Пусть есть функция f(x), заданная в некотором интервале (a, b). Точки х и х0 принадлежат этому интервалу. При изменении х меняется и сама функция. Изменение аргумента – разность его значений х-х0. Эта разность записывается как дельта икс и называется приращением аргумента. Изменением или приращением функции называется разность значений функции в двух точках. Определение производной:
Производная функции в точке – предел отношения приращения функции в данной точке к приращению аргумента, когда последнее стремится к нулю.
Иначе это можно записать так:
Какой смысл в нахождении такого предела? А вот какой:
Геометрический смысл производной: производная от функции в точке равна тангенсу угла между осью OX и касательной к графику функции в данной точке.
Физический смысл производной: производная пути по времени равна скорости прямолинейного движения.
Действительно, еще со школьных времен всем известно, что скорость – это частное пути x=f(t) и времени t. Средняя скорость за некоторый промежуток времени:
Чтобы узнать скорость движения в момент времени t0 нужно вычислить предел:
Кстати, о том, что такое пределы и как их решать, читайте в нашей отдельной статье.
Приведем пример, иллюстрирующий практическое применение производной. Пусть тело движется то закону:
Нам нужно найти скорость в момент времени t=2c. Вычислим производную:
Правила нахождения производных
Сам процесс нахождения производной называется дифференцированием. Функция, которая имеет производную в данной точке, называется дифференцируемой.
Как найти производную? Согласно определению, нужно составить отношение приращения функции и аргумента, а затем вычислить предел при стремящемся к нулю приращении аргумента. Конечно, можно вычислять все производные так, но на практике это слишком долгий путь. Все уже давно посчитано до нас. Ниже приведем таблицу с производными элементарных функций, а затем рассмотрим правила вычисления производных, в том числе и производных сложных функций с подробными примерами.
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Правило первое: выносим константу
Пример. Вычислим производную:
Правило второе: производная суммы функций
Производная суммы двух функций равна сумме производных этих функций. То же самое справедливо и для производной разности функций.
Не будем приводить доказательство этой теоремы, а лучше рассмотрим практический пример.
Найти производную функции:
Правило третье: производная произведения функций
Производная произведения двух дифференцируемых функций вычисляется по формуле:
Пример: найти производную функции:
Здесь важно сказать о вычислении производных сложных функций. Производная сложной функции равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной.
В вышеуказанном примере мы встречаем выражение:
В данном случае промежуточный аргумент – 8х в пятой степени. Для того, чтобы вычислить производную такого выражения сначала считаем производную внешней функции по промежуточному аргументу, а потом умножаем на производную непосредственно самого промежуточного аргумента по независимой переменной.
Правило четвертое: производная частного двух функций
Формула для определения производной от частного двух функций:
Мы постарались рассказать о производных для чайников с нуля. Эта тема не так проста, как кажется, поэтому предупреждаем: в примерах часто встречаются ловушки, так что будьте внимательны при вычислении производных.
С любым вопросом по этой и другим темам вы можете обратиться в студенческий сервис. За короткий срок мы поможем решить самую сложную контрольную и разобраться с заданиями, даже если вы никогда раньше не занимались вычислением производных.
Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.
Примеры работы функции ДЕЛЬТА для сравнения двух чисел в Excel
Функция ДЕЛЬТА в Excel используется для проверки двух числовых значений и возвращает два возможных варианта:
Примеры использования функции ДЕЛЬТА в Excel
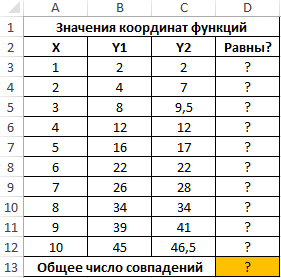
Пример 1. В таблице Excel указаны значения независимой координаты X и значения зависимых координат Y1 и Y2 для двух разных функций. Определить количество пар совпадающих значений.
Вид исходной таблицы данных:
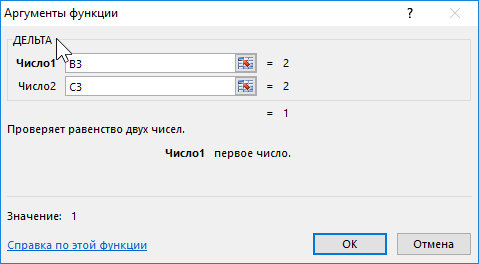
Для решения задачи сравним каждую пару значений зависимых координат Y1 и Y2 с помощью функции ДЕЛЬТА. В ячейке D3 запишем следующую формулу:
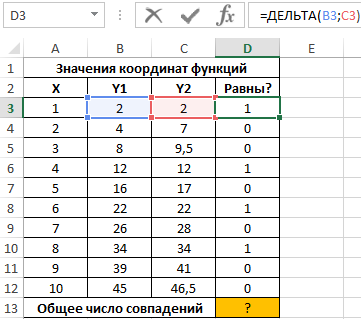
Полученное значение (1) свидетельствует о равенстве сравниваемых чисел. Протянем записанную в ячейке D3 формулу вниз до ячейки D12, чтобы автоматически рассчитать результаты для остальных значений Y1 и Y2:
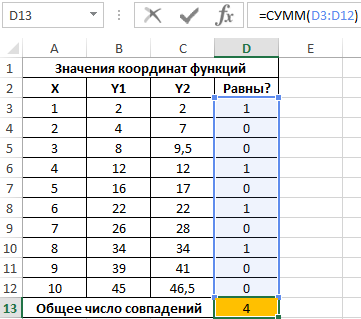
Для расчета числа пар совпадающих значений используем следующую функцию:
Всего 4 пары совпадений в значениях функций координат.
Калькулятор сроков возврата инвестиций в банковские депозиты
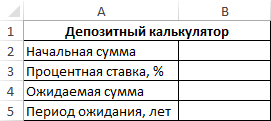
Пример 2. Реализовать калькулятор, который рассчитывает, сколько времени потребуется на получение определенной прибыли от депозита при известной начальной сумме вклада и годовой процентной ставки. Предусмотреть вывод сообщения об ошибке в случае, если одно или несколько исходных данных не указаны.
Вид формы для расчета:
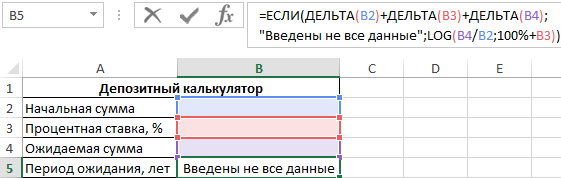
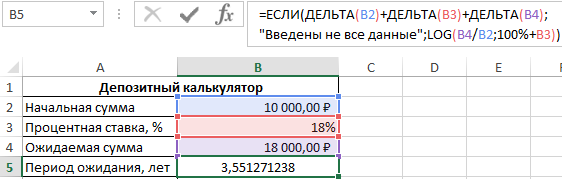
Поскольку для расчета используется логарифм из частного ожидаемой и начальной суммы с основанием в виде суммы депозита, выраженного в процентах (то есть 100%), и процентной ставки, то каждая ячейка из диапазона B2:B4 не должна являться пустой или принимать значение 0, поскольку логарифм нуля или логарифм с основанием 1 (100%) не может быть вычислен. Поэтому для расчетов используем следующую формулу:
В качестве проверочного выражения функции ЕСЛИ выступает значение, являющееся суммой возвращаемых результатов функциями ДЕЛЬТА. Последние сравнивают значения, содержащиеся в ячейках B2, B3 и B4 соответственно с 0 (второй аргумент явно не указан). Данный вариант записи соответствует логическому И (общий результат равен ИСТИНА, если все выражения, проверяемые функцией И, возвращают результат ИСТИНА). Полученное значение (0 или любое число от 1 до +∞) будет интерпретировано как ЛОЖЬ или ИСТИНА соответственно.
При незаполненных полях получим следующий результат:
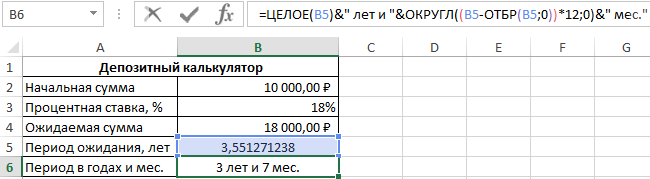
Напишем формулу для преобразования дробного числа в годы и месяцы:
В результате получим:
Расчет вероятности выпуска бракованной продукции на производстве в Excel
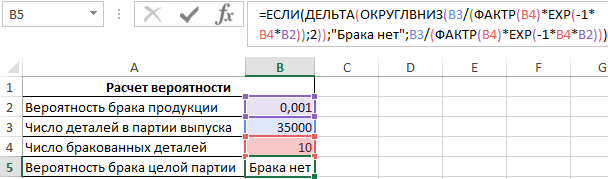
Пример 3. При изготовлении деталей на производственно-ремонтном заводе существует вероятность брака производимой продукции, которая равная коэффициенту 0,001. Определить, какая вероятность появления 10 выбракованных деталей (в этом случае вся партия считается браком) в партии из 35000 шт. Считается, что вероятностями ниже 10% можно пренебречь (то есть их приравнивают к нулю).
Вид исходной таблицы данных:
Для расчета используем следующую формулу:
Функция ОКРУГЛВНИЗ округляет до 0 все значения, которые меньше числа 0,01, то есть 10%-й вероятности. Функция ДЕЛЬТА принимает только один аргумент (выражение, полученное на основе формулы Пуассона для вычисления маловероятных случайных ситуаций), то есть сравнение выполняется с числом 0 (нуль).
Если вычислять формулу поэтапно, будет видно, что вероятность по формуле Пуассона равна примерно 0,00974 число1 ;[число2])
Примеры работы функции ДЕЛЬТА для сравнения двух чисел в Excel
Функция ДЕЛЬТА в Excel используется для проверки двух числовых значений и возвращает два возможных варианта:
Примеры использования функции ДЕЛЬТА в Excel
Пример 1. В таблице Excel указаны значения независимой координаты X и значения зависимых координат Y1 и Y2 для двух разных функций. Определить количество пар совпадающих значений.
Вид исходной таблицы данных:
Для решения задачи сравним каждую пару значений зависимых координат Y1 и Y2 с помощью функции ДЕЛЬТА. В ячейке D3 запишем следующую формулу:
Полученное значение (1) свидетельствует о равенстве сравниваемых чисел. Протянем записанную в ячейке D3 формулу вниз до ячейки D12, чтобы автоматически рассчитать результаты для остальных значений Y1 и Y2:
Для расчета числа пар совпадающих значений используем следующую функцию:
Всего 4 пары совпадений в значениях функций координат.
Калькулятор сроков возврата инвестиций в банковские депозиты
Пример 2. Реализовать калькулятор, который рассчитывает, сколько времени потребуется на получение определенной прибыли от депозита при известной начальной сумме вклада и годовой процентной ставки. Предусмотреть вывод сообщения об ошибке в случае, если одно или несколько исходных данных не указаны.
Вид формы для расчета:
Поскольку для расчета используется логарифм из частного ожидаемой и начальной суммы с основанием в виде суммы депозита, выраженного в процентах (то есть 100%), и процентной ставки, то каждая ячейка из диапазона B2:B4 не должна являться пустой или принимать значение 0, поскольку логарифм нуля или логарифм с основанием 1 (100%) не может быть вычислен. Поэтому для расчетов используем следующую формулу:
В качестве проверочного выражения функции ЕСЛИ выступает значение, являющееся суммой возвращаемых результатов функциями ДЕЛЬТА. Последние сравнивают значения, содержащиеся в ячейках B2, B3 и B4 соответственно с 0 (второй аргумент явно не указан). Данный вариант записи соответствует логическому И (общий результат равен ИСТИНА, если все выражения, проверяемые функцией И, возвращают результат ИСТИНА). Полученное значение (0 или любое число от 1 до +∞) будет интерпретировано как ЛОЖЬ или ИСТИНА соответственно.
При незаполненных полях получим следующий результат:
Напишем формулу для преобразования дробного числа в годы и месяцы:
В результате получим:
Расчет вероятности выпуска бракованной продукции на производстве в Excel
Пример 3. При изготовлении деталей на производственно-ремонтном заводе существует вероятность брака производимой продукции, которая равная коэффициенту 0,001. Определить, какая вероятность появления 10 выбракованных деталей (в этом случае вся партия считается браком) в партии из 35000 шт. Считается, что вероятностями ниже 10% можно пренебречь (то есть их приравнивают к нулю).
Вид исходной таблицы данных:
Для расчета используем следующую формулу:
Функция ОКРУГЛВНИЗ округляет до 0 все значения, которые меньше числа 0,01, то есть 10%-й вероятности. Функция ДЕЛЬТА принимает только один аргумент (выражение, полученное на основе формулы Пуассона для вычисления маловероятных случайных ситуаций), то есть сравнение выполняется с числом 0 (нуль).
Если вычислять формулу поэтапно, будет видно, что вероятность по формуле Пуассона равна примерно 0,00974 число1 ;[число2])
Дюжина вопросов о «дельта»-штамме
1. Чем отличается штамм дельта от изначальной версии COVID-19?
Штамм «дельта» был впервые описан в Индии в декабре 2020 года и с тех пор активно распространился в более чем сотне стран мира.
Он отличается от привычного «уханьского» варианта рядом мутаций в гене S-белка. Вероятно, именно эти мутации позволяют ему «ускользать» от действия нейтрализующих антител у лиц, ранее переболевших коронавирусной инфекцией.
2. Как часто в настоящее время встречается «дельта» вариант?
В июле штамм «дельта» стал превалирующим во многих странах мира, на сегодняшний день до 70% всех случаев инфицирования связывают с этим штаммом коронавируса. В России сейчас около 68% случаев коронавируса приходится именно на этот генетический вариант, а в крупных мегаполисах его распространенность еще выше.
3. Действительно ли он более заразный?
Согласно научным данным индекс репродукции (то есть способность заражать) «дельта»-варианта увеличился в 2-2,5 раза. Если раньше носитель инфекции мог заразить 1-2 человека до момента выявления заболевания, то теперь это число доходит до 5-6. Именно поэтому при отслеживании контактных Роспотребнадзор для «дельта»-варианта берет под наблюдение большее количество людей.
4. Правда ли, что у дельта-варианта более короткий инкубационный период?
5. Правда ли, что течение заболевания, вызванного штаммом «дельта» более тяжелое и длительное?
Течение болезни при дельта-варианте коронавирусной инфекции может отличаться большей стремительностью. Важно следить за состоянием и своевременно обращаться за медицинской помощью.
6. Каковы симптомы при заражении дельта-вариантом? Изменился ли процент бессимптомных пациентов?
Чаще всего симптомы заболевания, вызванного дельта-вариантом остаются классическими для COVID-19: лихорадка, кашель, потеря обоняния и вкуса. Однако, врачи также наблюдают симптомы, характерные для ОРВИ и кишечной инфекции: насморк, головные боли, боль в горле, а также отмечают симптоматику со стороны ЖКТ – диарею, реже тошноту и рвоту.
7. Чаще ли дельта заражает молодых?
Штамм коронавируса «дельта» действительно «помолодел», говорят ученые. При этом почти половина всех пациентов сегодня заражаются в кругу семьи или друзей. Самая уязвимая категория – молодые люди от 14 до 29 лет. Это активные люди с самым большим количеством контактов, которые часто пользуются общественным транспортом, ходят на работу, общаются в нерабочее время.
8. Можно ли узнать, что человек инфицирован именно этим штаммом?
10. Выявляет ли стандартный ПЦР-тест заболевание, если оно вызвано штаммом «дельта»? Какова диагностика штамма «дельта»?
Да, стандартный ПЦР-тест, выполненный в соответствии с рекомендациями по забору и в правильные сроки выявит заболевание коронавирусом, даже варианта «дельта». Но надо помнить, что ПЦР-тесты выявляют наличие или отсутствие у человека вируса SARS-CoV2, вызывающего COVID-19, но не выявляют каким именно вариантом/штаммом вируса вызвано заболевание.
В настоящее время существуют более сложные тесты, способные определять конкретные мутации, и по которым можно идентифицировать штамм. Они имеют скорее научное, а не практическое значение, поэтому не особенно востребованы в коммерческих диагностических лабораториях.
11. Существует ли специальная терапия для пациентов с этим вариантом коронавирусной инфекции?
По данным специалистов, клинические рекомендации по лечению пациентов с новым вариантом коронавирусной инфекции в настоящее время принципиально не изменились.
12. Какие меры профилактики существуют? И будут ли работать вакцины?
Имеющиеся на данный момент исследования и результаты наблюдений указывают на то, что защитный эффект вакцин от COVID-19 против варианта «дельта» может снижаться. Поэтому методическими рекомендациями показана ревакцинация раз в полгода для достаточной защиты от новых штаммов. Но существующие вакцины по-прежнему обладают хорошими профилактическими и защитными свойствами против данного штамма, а также, в случае заболевания, против тяжелых форм заболевания коронавирусом.
Примеры работы функции ДЕЛЬТА для сравнения двух чисел в Excel
Функция ДЕЛЬТА в Excel используется для проверки двух числовых значений и возвращает два возможных варианта:
Примеры использования функции ДЕЛЬТА в Excel
Пример 1. В таблице Excel указаны значения независимой координаты X и значения зависимых координат Y1 и Y2 для двух разных функций. Определить количество пар совпадающих значений.
Вид исходной таблицы данных:
Для решения задачи сравним каждую пару значений зависимых координат Y1 и Y2 с помощью функции ДЕЛЬТА. В ячейке D3 запишем следующую формулу:
Полученное значение (1) свидетельствует о равенстве сравниваемых чисел. Протянем записанную в ячейке D3 формулу вниз до ячейки D12, чтобы автоматически рассчитать результаты для остальных значений Y1 и Y2:
Для расчета числа пар совпадающих значений используем следующую функцию:
Всего 4 пары совпадений в значениях функций координат.
Калькулятор сроков возврата инвестиций в банковские депозиты
Пример 2. Реализовать калькулятор, который рассчитывает, сколько времени потребуется на получение определенной прибыли от депозита при известной начальной сумме вклада и годовой процентной ставки. Предусмотреть вывод сообщения об ошибке в случае, если одно или несколько исходных данных не указаны.
Вид формы для расчета:
Поскольку для расчета используется логарифм из частного ожидаемой и начальной суммы с основанием в виде суммы депозита, выраженного в процентах (то есть 100%), и процентной ставки, то каждая ячейка из диапазона B2:B4 не должна являться пустой или принимать значение 0, поскольку логарифм нуля или логарифм с основанием 1 (100%) не может быть вычислен. Поэтому для расчетов используем следующую формулу:
В качестве проверочного выражения функции ЕСЛИ выступает значение, являющееся суммой возвращаемых результатов функциями ДЕЛЬТА. Последние сравнивают значения, содержащиеся в ячейках B2, B3 и B4 соответственно с 0 (второй аргумент явно не указан). Данный вариант записи соответствует логическому И (общий результат равен ИСТИНА, если все выражения, проверяемые функцией И, возвращают результат ИСТИНА). Полученное значение (0 или любое число от 1 до +∞) будет интерпретировано как ЛОЖЬ или ИСТИНА соответственно.
При незаполненных полях получим следующий результат:
Напишем формулу для преобразования дробного числа в годы и месяцы:
В результате получим:
Расчет вероятности выпуска бракованной продукции на производстве в Excel
Пример 3. При изготовлении деталей на производственно-ремонтном заводе существует вероятность брака производимой продукции, которая равная коэффициенту 0,001. Определить, какая вероятность появления 10 выбракованных деталей (в этом случае вся партия считается браком) в партии из 35000 шт. Считается, что вероятностями ниже 10% можно пренебречь (то есть их приравнивают к нулю).
Вид исходной таблицы данных:
Для расчета используем следующую формулу:
Функция ОКРУГЛВНИЗ округляет до 0 все значения, которые меньше числа 0,01, то есть 10%-й вероятности. Функция ДЕЛЬТА принимает только один аргумент (выражение, полученное на основе формулы Пуассона для вычисления маловероятных случайных ситуаций), то есть сравнение выполняется с числом 0 (нуль).
Если вычислять формулу поэтапно, будет видно, что вероятность по формуле Пуассона равна примерно 0,00974 число1 ;[число2])