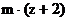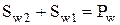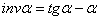Что такое делительный окружной шаг зубьев выбрать наиболее точную формулировку

Что такое делительный окружной шаг зубьев? Выбрать наиболее точную формулировку.

1. расстояние между профилями соседних зубьев

2. расстояние между одноименными профилями соседних зубьев по делительной окружности

3. ширина зуба по делительной окружности

4. длина дуги делительной окружности между соседними зубьями

64. Укажите формулу для определения диаметра окружности выступов цилиндрического зубчатого колеса

1.

2.

3.

4.

Какие параметры цилиндрической зубчатой передачи стандартизованы?

66. Указать формулу для определения диаметра делительной окружности цилиндрической зубчатой передачи

1.

2.

3.

4.

Каково основное достоинство конических зубчатых передач?

1. простота изготовления и монтажа

2. малые габаритные размеры и вес

3. равномерность распределения нагрузки в зацеплении

4. возможность соединения валов с пересекающимися осями

Каковы основные недостатки прямозубых конических зубчатых передач?

1. оси колес пересекаются

2. сложность изготовления, монтажа и обслуживания

3. невысокая точность передачи

4. непостоянство передаточного отношения

Какова основная причина выхода из строя зубчатых передач, работающих в масле?

1. значительный износ рабочей поверхности зуба

3. выкрашивание рабочей поверхности зуба

4. заклинивание подшипников

Какова основная причина выхода из строя открытых зубчатых переда?

1. усталостные микротрещины

2. износ рабочей поверхности зуба

3. выкрашивание рабочей поверхности зуба

По какой из механических характеристик определяют допускаемое контактное напряжение зубчатых колес?

С какими напряжениями при работе передачи связана поломка зуба?

1. с напряжениями сжатия

2. с напряжениями сдвига

3. с контактными напряжениями

4. с напряжениями изгиба

Указать основные преимущества косозубых передач по сравнению с прямозубыми.

1. меньшее усилие на опорах

2. отсутствие периода однопарного зацепления

3. низкая стоимость и доступность материала

4. простота зубонарезания

Какова основная причина ограничения величины угла наклона зуба в цилиндрической косозубой передаче?

1. увеличение коэффициента перекрытия

2. увеличение концентрации напряжений в зацеплении

3. увеличение осевой нагрузки на подшипники

4. увеличение габаритных размеров

Указать основной недостаток цилиндрических косозубых передач?

1. увеличение габаритных размеров

2. увеличение осевой нагрузки на опоры

3. усиленный износ рабочей поверхности зуба

4. увеличение коэффициента перекрытия

Указать основное достоинство шевронной передачи

1. увеличение суммарной длины контактной линии

2. увеличение коэффициента перекрытия

3. необходимость более высокой точности изготовления

4. отсутствие осевого нагружения опор

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).

Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.

Источник

Детали машин

Геометрические параметры эвольвентного зацепления

Эвольвентное зацепление зубчатых колес характеризуется различными геометрическими параметрами, оказывающими существенное влияние на свойства и работу передачи. К таким параметрам относятся диаметры начальной, основной и делительной окружностей, окружной шаг зубьев, модуль зацепления, высота головок и ножек зубьев, длина активной линии зацепления, угол наклона линии зуба косозубого колеса, коэффициент перекрытия и некоторые другие.

В обозначении геометрических параметров зацепления используют индексы, относящиеся к характерным окружностям зубчатых колес:

Параметрам, относящимся к делительной окружности, индекс не присваивается.

Начальные окружности

Начальными называют окружности, которые в процессе зацепления перекатываются одна по другой без скольжения (рис. 1), при этом отношение их радиусов (расстояний от центров О₁ и О₂ до полюса П ) при неизменном межосевом расстоянии О₁О₂ тоже остается неизменным.
При изменении межосевого расстояния a_w меняются и диаметры d_w начальных окружностей шестерни и колеса, т. е. у пары зубчатых колес может быть множество начальных окружностей.
У отдельно взятого колеса начальной окружности не существует – по определению этот параметр образуется в зацеплении, т. е. в зубчатой передаче.

Межосевое расстояние определяется по формуле:

Делительная окружность

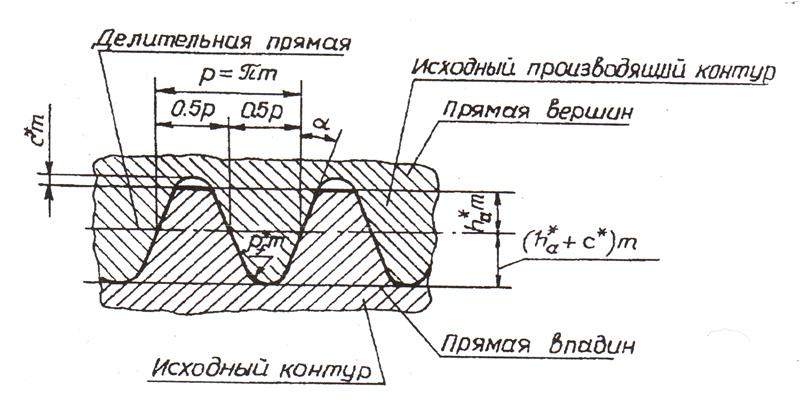
Окружность, на которой шаг p и угол зацепления α соответственно равны шагу p и углу α профиля инструментальной рейки, называют делительной окружностью (рис. 1). Эта окружность принадлежит отдельно взятому колесу, ее диаметр d при изменении межосевого расстояния остается неизменным.

Делительные окружности совпадают с начальными, если межосевое расстояние пары зубчатых колес равно сумме радиусов делительных окружностей.

У большинства зубчатых передач диаметры делительных и начальных окружностей совпадают, т. е.:

Исключение составляют передачи с угловой модификацией.

Окружной шаг зубьев

Расстояние между одноименными сторонами двух соседних зубьев, взятое по дуге делительной окружности, называют окружным шагом зубьев по делительной окружности и обозначают буквой p (рис. 1).
Для пары зацепляющихся зубчатых колес окружной шаг зубьев должен быть одинаковым.

Основной шаг

Окружная толщина зуба и окружная ширина впадины

Окружной модуль зубьев

Модуль зубьев m – часть диаметра делительной окружности, приходящаяся на один зуб.

Модуль является основной характеристикой размера зубьев. Для пары зацепляющихся колес модуль должен быть одинаковым.

Для обеспечения взаимозаменяемости зубчатых колес и унификации дорогостоящего зубонарезного оборудования и инструмента значения m регламентируются стандартом в диапазоне от 0,05 до 100 мм.
В соответствии со стандартным рядом I модуль может принимать следующие значения: 1,0, 1,25, 1,5, 2,0, 2,5, 3,0, 4,0, 5,0, 6,0, 8,0, 10,0.
Стандартный ряд II значительно расширяет диапазон применяемых на практике модулей ( m = 1,125, 1,375, 1,75 и т. д.).

При выборе модулей из стандартных рядов первый ряд следует предпочитать второму.

Высота головки и ножки зуба

Длина активной линии зацепления

Коэффициент торцового перекрытия

Коэффициентом торцового перекрытия ε_α называют отношение длины активной линии зацепления к основному шагу:

где z₁ и z₂ – числа зубьев шестерни и колеса; β – угол наклона линии зуба косозубого колеса.

Непрерывность работы зубчатой передачи возможна при условии, когда последующая пара зубьев входит в зацепление до выхода предыдущей, т. е. когда обеспечивается перекрытие работы одной пары зубьев другой. Чем больше пар зубьев одновременно находится в зацеплении, тем выше плавность работы передачи.

Источник

Окружной шаг зубчатого колеса

Зубчатые передачи широко применяют в транспортных, сельскохозяйственных машинах и в промышленном оборудовании. С их помощью изменяют по величине и направлению скорости движущихся частей станков и передают от одного вала к другому усилия и крутящие моменты. Крутящий момент равен произведению силы на плечо, кГм.

Рис. 116. Основные элементы зубчатого колеса

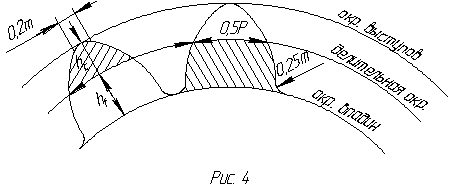
Элементы зубчатого колеса. В каждом зубчатом колесе (рис. 116) различают три окружности: делительную окружность, окружность выступов, окружность впадин, а следовательно, три соответствующих им диаметра.

Окружность впадин зубчатого колеса проходит по основанию впадин зубьев и обозначается D i.

Расстояние между серединами двух соседних зубьев, измеренное по дуге делительной окружности, называется и обозначается буквой t.

Величина элемента зубчатого колеса задается в долях модуля (m). Модуль показывает долю диаметра начальной окружности в миллиметрах, приходящуюся на один зуб, т. е,

где z – число зубьев зубчатого колеса.

Если шаг, выраженный в миллиметрах, разделить на число π=3,14, то также получим модуль, т. е. m=t/π мм, а тогда шаг будет t=mπ.

Радиальный зазор δ (см. рис. 118,б)-кратчайшее расстояние между вершиной зуба и основанием впадины сопряженного колеса.

Боковой зазор зубчатого колеса С п (см. рис. 118, б)-кратчайшее расстояние между нерабочими профильными поверхностями смежных зубьев, когда их рабочие поверхности находятся в контакте.

С модулем связаны все элементы зубчатого колеса:

высота головки зуба h’ = m;

высота ножки зуба h» =1,25 m;

высота всего зуба h= h’+h»=m+1,25m = 2,25m.

Зная число зубьев z, с помощью модуля можно определить диаметр делительной окружности зубчатого колеса.

Диаметр окружности выступов (диаметр заготовки зубчатого колеса) вычисляют по формуле:

Формулы, с помощью которых можно определить параметры цилиндрических зубчатых колес в зависимости от модуля и числа зубьев z, приведены в табл. 8.

Таблица 8 Формулы для расчета параметров цилиндрических зубчатых колес

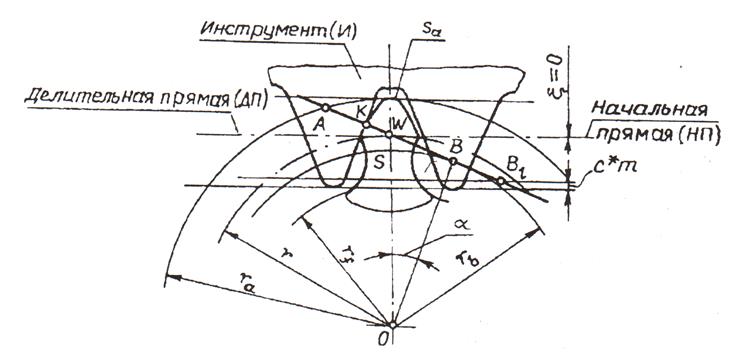
Возможны три варианта расположения средней линии инструментальной рейки относительно делительной окружности колеса.

Коэффициент смещения Х в этом случае считается положительным.

3. Средняя прямая С-С смещена к центру на величину Хm, при чем коэффициент смещения Х считается отрицательным (рис. 1.35 в).

Зубчатые колеса, нарезанные со сдвигом рейки, называются исправленными колесами. Колеса, нарезанные с положительным сдвигом, называют положительными. А нарезанные с отрицательным сдвигом – отрицательными. Колеса, нарезаемые без сдвига, называют нулевыми колесами.

Для того чтобы, определить к какой из этих групп относится зубчатое колесо, надо определить толщину его зубьев по делительной окружности.

В зависимости от смещений каждого колеса можно получить три типа передач отличающихся расположением начальных и делительных окружностей.

то есть, передачи, составленные из колес без смещения и передачи в которых отрицательное смещение одного колеса равно по абсолютной величине положительному смещению другого колеса (равносмещенные).

Межосевое расстояние в этих передачах называется делительным межосевым расстоянием, а угол зацепления равен углу профиля производящего контура.

II тип (рис. 1.36 б). В передачах, у которых по делительным окружностям толщина зуба одного колеса больше ширины впадины другого, для зацепления без бокового зазора межцентровое расстояние должно быть больше а.

Геометрический расчет зубчатых передач при заданных смещениях X 1 и X 2

Для вычисления и определяем сначала толщину зуба по начальной окружности.

Из (рис. 1.37) с учетом уравнения эвольвенты имеем:

Подставив значение толщины зуба по делительной окружности:

И ,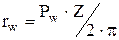

где – шаг по начальной окружности получаем:

Для начальных окружностей сумма толщин зубьев равна шагу

Отсюда с учетом формулы (1.15)

Радиусы начальных окружностей определим из

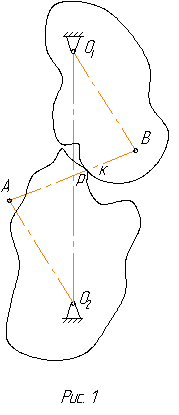
ЗУБЧАТЫЕ МЕХАНИЗМЫ находят самое широкое применение в машинах. Они используются для изменения угловой скорости ведомого звена. При этом совершенно необходимым является требование постоянства передаточного отношения не только за целые обороты зубчатых колес, но и в течение зацепления каждой пары зубьев. Условие, которому должны удовлетворять профили зубьев для сохранения постоянного передаточного отношения, определяется теоремой зацепления, гласящей о том, что общая нормаль АВ к профилям зубчатых колес П1 и П2 в точке касания К делит МЕЖЦЕНТРОВОЕ РАССТОЯНИЕ О1 О2 НА ЧАСТИ, ОБРАТНО ПРОПОРЦИОНАЛЬНЫЕ УГЛОВЫМ СКОРОСТЯМ. Точка пересечения нормали и межцентрового расстояния называется ПОЛЮСОМ ЗАЦЕПЛЕНИЯ (Р) (Рис.I). Итак, передаточное отношение

где – угловые скорости колес

Начальные окружности колес

Для того чтобы передаточное отношение было постоянным, необходимо выбрать такой профиль зубьев, для которого при зацеплении пары зубьев в любом положении полюс зацепления Р сохранял свое положение на линии центров. Этому условию удовлетворяют профили зубьев, очерченные эвольвентами окружностей.

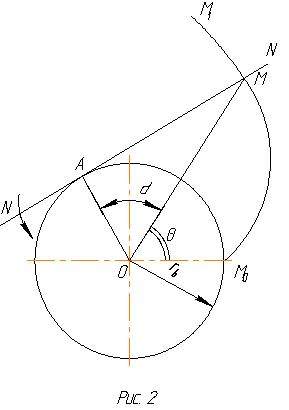
ЭВОЛЬВЕНТНОЙ называется кривая МОМ1, описываемая точкой М прямой NN, которая катится без скольжения по окружности радиуса rB=OA (Рис.2). Из построения видно, что эвольвента будет располагаться вне окружности радиуса rB и начинается на этой окружности. Окружность, по которой катится прямая, называется ОСНОВНОЙ ОКРУЖНОСТЬЮ.

радиус вектор эвольвенты находится из

где – эвольвентная функция

– угол давления на уровне радиуса

Тригонометрическую функцию называют инволютой угла т.е.

На рис.8 показано зацепление двух зубьев. Нормаль к профилям зубьев в общей точке М их контакта проходит через полюс Р и по свойству эвольвенты касается основных окружностей колес. При вращении колес точка контакта М перемещается по этой внутренней касательной, которая является линией зацепления. Давление от колеса к колесу передается по линии зацепления под углом к линии являющейся общей касательной к начальным окружностям колес. Угол называется УГЛОМ ЗАЦЕПЛЕНИЯ.

На рис. 4 изображена часть зубчатого колеса. Боковые поверхности зубьев очерчены по эвольвенте. Расстояние между односторонними профилями двух смежных зубьев колеса, взятое по дуге, называется ШАГОМ ЗАЦЕПЛЕНИЯ.

ДЕЛИТЕЛЬНОЙ ОКРУЖНОСТЬЮ называется такая окружность, по которой шаг равен стандартному шагу. Число зубьев колеса – z должно быть целым, поэтому шаг зацепления должен быть кратен длине окружности, по которой он откладывается. Следовательно, если обозначить через радиус r – радиус делительной окружности колеса, Р – окружной шаг по этой окружности и z – число зубьев колеса, то должны иметь место равенства.

Величина m – отношение окружного шага к числу называемое модулем зубьев. Модуль измеряется в миллиметрах и служит основным параметром, определяющим размеры зубчатого колеса и его элементов. Значение модуля определяется стандартом.

Зубчатое колесо называется НУЛЕВЫМ, если по делительной окружности толщина зуба S равна ширине впадины S В. размеры ЭЛЕМЕНТОВ НУЛЕВЫХ КОЛЕС, выраженных через модуль, приведены в таблице.

Радиус делительной окружности

Высота головки зуба

Радиус окружности выступов

Радиус окружности впадин

Толщина зуба по делительной окружности

Радиус основной окружности

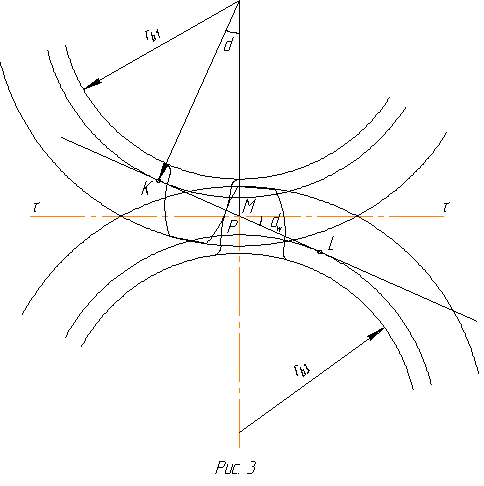
При нарезании зубчатых колес методом обкатки инструмент изготовляется либо в виде колеса с эвольвентными профилями зубьев (так называемый долбяк), либо – зубчатой рейки с прямолинейными профилями зубьев (так называемая гребенка). В процессе нарезания зубчатого колеса заготовке и инструменту сообщается такое относительное движение, какое они имели бы, находясь в зацеплении.

Инструмент имеет дополнительное возвратно-поступательное движение вдоль оси колеса, во время осуществления которого режущая кромка инструмента вырезает на заготовке профиль зуба.

Из рис.5 видно, что шаг рейки имеет одинаковую величину по любой прямой (0-0 или I-I), параллельной основанию рейки. Можно провести такую линию 0-0, по которой толщина зуба равна ширине впадины. Эта линия называется модульной прямой рейки.

Для того, чтобы нарезать нулевое колесо, необходимо установить гребенку так, чтобы модульная прямая ее была удалена от центра заготовки на расстояние радиуса делительной окружности r, т.е. чтобы делительная окружность заготовки обкатывалась без скольжения по модульной прямой. Тогда на нарезаемом колесе получатся зубья, толщина которых по делительной окружности будет равна ширине впадины.

Пусть мы отодвинули рейку от центра заготовки колеса на величину xm. Тогда при нарезании зубьев делительная окружность будет катится без скольжения по линии I-I, которую назовем начальной прямой. Из рисунка видно, что в этом случае толщина зуба гребенки на начальной прямой будет меньше впадины, значит, на нарезаемом колесе по делительной окружности толщина зуба будет больше, чем ширина впадины (так как при обкатке зуб рейки образует на заготовке впадину). Зубчатые колеса, нарезанные методом обкатки с удалением гребенки от центра заготовки, по сравнению с нулевой установкой, при которой делительная окружность касается модульной прямой, называются ПОЛОЖИТЕЛЬНЫМИ КОЛЕСАМИ, а дополнительное удаление гребенки – ПОЛОЖИТЕЛЬНЫМ СМЕЩЕНИЕМ (СДВИГОМ).(Рис.6).

Можно дать гребенке отрицательное смещение (сдвиг), т.е. приблизить ее к центру заготовки по сравнению с нулевой установкой. Тогда на заготовке будет нарезано целое число зубьев с очертанием бокового профиля их по эвольвенте. Однако в этом случае по делительной окружности толщина зуба будет меньше ширины впадины. Такое колесо называется ОТРИЦАТЕЛЬНЫМ. Отношение смещения к модулю называется КОЭФФИЦИЕНТОМ СМЕЩЕНИЕМ (ОТНОСИТЕЛЬНЫМ СДВИГОМ) и обозначается через x.

Изготовление положительных, так называемых корригированных, колес производится с целью увеличения прочности зубьев (устранения подреза профиля малого колеса), уменьшения наибольших значений удельного скольжения.

Корригированные колеса могут быть введены в сцепления между собой и с нулевыми колесами. Формулы для расчета элементов корригированных колес и их зацепления приведены в таб.1.

Лабораторная работа № 10

Профилирование эвольвентных зубьев

Цель работы: освоение методики нарезания эвольвентных зубчатых колес по методу огибания (обкатки) с различными смещениями инструмента; расчет геометрии эвольвентного зацепления.

Оборудование: прибор для профилирования зубьев ТММ-42, прибор для нарезания бумажных кругов, бумажный круг, остро заточенный карандаш.

Краткие теоретические сведения

Метод огибания при изготовлении эвольвентных зубчатых колес

Зубчатые колеса изготовляют двумя основными способами: копированием и огибанием. Наиболее совершенным по точности профиля и производительности является способ огибания (рис. 10.1). При изготовлении колеса этим способом профили его зубьев образуются как огибающие к семейству положений профилей зубьев производящего колеса (инструмента). Если производящее колесо имеет зубья с эвольвентным профилем (долбяк, рис. 10.1, а ), то на заготовке в результате обработки этим способом получают зубья также с эвольвентными профилями. При радиусе колеса, равном бесконечности, инструмент преображается в рейку с прямолинейными профилями зубьев (гребенка, 10.1, б ). Такие профили зубьев инструмента просты и технологичны, позволяют изготавливать инструмент с высокой точностью. Наиболее высокопроизводительным методом является нарезание зубчатых колес модульной червячной фрезой (рис. 10.1, в ).

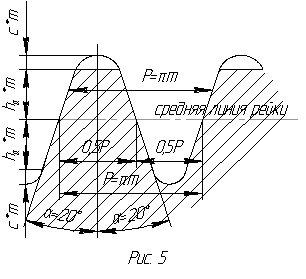
Метод огибания позволяет одним и тем же инструментом нарезать колёса с различными числами зубьев и различными формами профиля зубьев, которые определяются не только размерами инструмента, но и его расположением относительно заготовки. Геометрические параметры нарезаемого цилиндрического колеса определяют модулем m и параметрами стандартного исходного контура по ГОСТ 13755: углом профиля α = 20º; коэффициентом высоты головки зуба = 1; коэффициентом радиального зазора с* = 0,25; коэффициентом радиуса переходной кривой = 0,38 (рис. 10.2).

Рис. 10.2. Исходные контуры

Нулевое зубчатое колесо нарезают без смещения, то есть xm = 0 и x = 0

(рис. 10.3). В станочном зацеплении начальными являются делительная прямая инструмента и делительная окружность колеса. Так как перекатывание их друг по другу происходит без скольжения,то на делительной окружности нулевого

колеса толщина зуба равна ширине впадины :

Рис. 10.3. Нарезание нулевого колеса

Положительное зубчатое колесо с коэффициентом смещения хт > 0 (рис. 10.4) получают при смещении инструмента в радиальном направлении от центра заготовки . На делительной окружности колеса с положительным смещением толщина зуба больше ширины впадины и равна:

Отрицательное зубчатое колесо с коэффициентом смещения х

Главная » Компоненты » Окружной шаг зубчатого колеса формула. Профилирование эвольвентных зубьев

Геометрические параметры эвольвентного зацепления

Эвольвентное зацепление зубчатых колес характеризуется различными геометрическими параметрами, оказывающими существенное влияние на свойства и работу передачи. К таким параметрам относятся диаметры начальной, основной и делительной окружностей, окружной шаг зубьев, модуль зацепления, высота головок и ножек зубьев, длина активной линии зацепления, угол наклона линии зуба косозубого колеса, коэффициент перекрытия и некоторые другие.

В обозначении геометрических параметров зацепления используют индексы, относящиеся к характерным окружностям зубчатых колес:

Параметрам, относящимся к делительной окружности, индекс не присваивается.

При обозначении параметров пары зубчатых колес индекс «1» присваивается шестерне, «2» – колесу.

Начальные окружности

Начальными называют окружности, которые в процессе зацепления перекатываются одна по другой без скольжения (рис. 1), при этом отношение их радиусов (расстояний от центров О₁ и О₂ до полюса П ) при неизменном межосевом расстоянии О₁О₂ тоже остается неизменным.
При изменении межосевого расстояния a_w меняются и диаметры d_w начальных окружностей шестерни и колеса, т. е. у пары зубчатых колес может быть множество начальных окружностей.
У отдельно взятого колеса начальной окружности не существует – по определению этот параметр образуется в зацеплении, т. е. в зубчатой передаче.

Межосевое расстояние определяется по формуле:

Делительная окружность

Окружность, на которой шаг p и угол зацепления α соответственно равны шагу p и углу α профиля инструментальной рейки, называют делительной окружностью (рис. 1). Эта окружность принадлежит отдельно взятому колесу, ее диаметр d при изменении межосевого расстояния остается неизменным.

Делительные окружности совпадают с начальными, если межосевое расстояние пары зубчатых колес равно сумме радиусов делительных окружностей.

У большинства зубчатых передач диаметры делительных и начальных окружностей совпадают, т. е.:

Исключение составляют передачи с угловой модификацией.

Окружной шаг зубьев

Расстояние между одноименными сторонами двух соседних зубьев, взятое по дуге делительной окружности, называют окружным шагом зубьев по делительной окружности и обозначают буквой p (рис. 1).
Для пары зацепляющихся зубчатых колес окружной шаг зубьев должен быть одинаковым.

Основной шаг

Окружная толщина зуба и окружная ширина впадины

Окружной модуль зубьев

Модуль зубьев m – часть диаметра делительной окружности, приходящаяся на один зуб.

Модуль является основной характеристикой размера зубьев. Для пары зацепляющихся колес модуль должен быть одинаковым.

Для обеспечения взаимозаменяемости зубчатых колес и унификации дорогостоящего зубонарезного оборудования и инструмента значения m регламентируются стандартом в диапазоне от 0,05 до 100 мм.
В соответствии со стандартным рядом I модуль может принимать следующие значения: 1,0, 1,25, 1,5, 2,0, 2,5, 3,0, 4,0, 5,0, 6,0, 8,0, 10,0.
Стандартный ряд II значительно расширяет диапазон применяемых на практике модулей ( m = 1,125, 1,375, 1,75 и т. д.).

При выборе модулей из стандартных рядов первый ряд следует предпочитать второму.

Высота головки и ножки зуба

Длина активной линии зацепления

Коэффициент торцового перекрытия

Коэффициентом торцового перекрытия ε_α называют отношение длины активной линии зацепления к основному шагу:

где z₁ и z₂ – числа зубьев шестерни и колеса; β – угол наклона линии зуба косозубого колеса.

Непрерывность работы зубчатой передачи возможна при условии, когда последующая пара зубьев входит в зацепление до выхода предыдущей, т. е. когда обеспечивается перекрытие работы одной пары зубьев другой. Чем больше пар зубьев одновременно находится в зацеплении, тем выше плавность работы передачи.

Источник