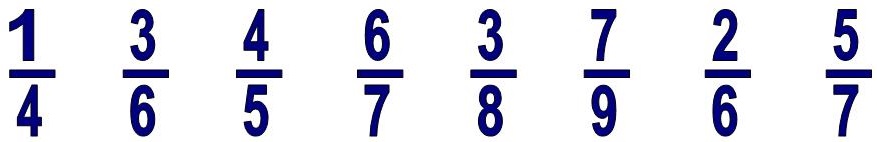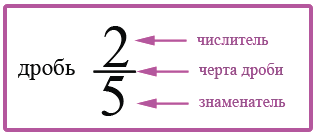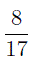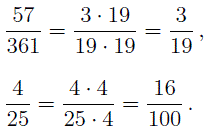Что такое делитель и числитель
Дроби и доли.
Дроби самая сложная тема для учеников начальных классов. Но даже самая трудная тема может стать простой и понятной. Для обучения детей нужно использовать фантазию и элементы игры. А главное – сохранять спокойствие.
В серьезных учебниках по математике есть знаки: и сложение, и вычитание, и умножение. А вот, привычного нам, с вами знака деления (:) – нет. Получается, что знаком деления (:) пользуются только ученики начальной школы? На самом деле – нет. Только этот знак можно писать и по-другому, вот такой чертой, она пишется посередине клетки:
Вот это все – деление.
Деление можно записывать не двумя точками, а горизонтальной полоской.
Так вот: любая математическая запись, в которой присутствует знак деления в виде черточки, называется дробью.
Слово «дробь» говорит само за себя – оно обозначает дробление или деление.
Для записи дробей используются цифры и черта, которую называют дробной.
Вы когда-нибудь видели военный парад? Идут солдаты стройными рядами, а впереди человек со знаменем (флагом) – знаменосец! И по знамени легко понять, к какому роду войск принадлежат эти солдаты. У дроби тоже есть «знаменосец» — это главное число, которое обозначает, на сколько равных частей разделили целое (предмет, фигуру или величину).
«Знаменосец» пишется под дробной чертой и называется ЗНАМЕНАТЕЛЬ.
А число, над чертой показывает, сколько таких частей взяли (или закрасили, или съели). Это число называют ЧИСЛИТЕЛЕМ.
читается – две третьих, можно заменить по-другому — 2 : 3.
Рассмотрим еще одно число: раньше мы не могли на уроке математики 1 разделить на 2. А теперь – умеем: 1 разделить на 2 – это не что иное, как одна вторая. Что же это значит? Если в математике мы с вами не делали этого ни разу, то в жизни вы это делаем постоянно. Предположим, у вас есть яблоко. И вам нужно разделить его между вами и другом. Т.е. одно яблоко разделить на 2.
Так что же за число такое – одна вторая, во-первых, это дробь потому что присутствует знак деления, во-вторых, оно меньше единицы.
Потому что нельзя один разделить на 2, чтобы получилось что-то больше 1.
В-третьих, оно обозначает, что мы целое разделили на 2 и взяли себе одну такую часть.
Давайте посмотрим на число:
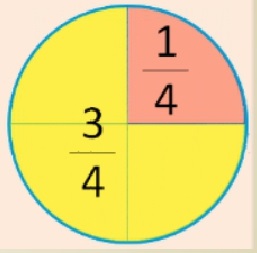
По правилу, которое мы с вами вывели: три четвертых – это тоже самое, что три разделить на 4.
Давайте посмотрим, как это понять. Круг разделим на 4 равные части.
3 части закрасим желтым цветом. Это и есть три четвертых. Что же это значит?
Во-первых, это тоже дробь.
Во-вторых, она тоже меньше единицы.
И она обозначает, что круг мы разделили на 4 части
и закрасили желтым цветом – 3 таких части.
Итак,
как вы уже поняли: любая дробь будет иметь черту.
Ее так и называют – дробная черта. И обязательно будет стоять какое-то число над чертой и какое-то число под чертой.
Давайте научимся, как правильно читать дроби.
Читают их так: верхнее число всегда будет отвечать на вопрос: сколько?, а нижнее будет отвечать на вопрос: какая? или каких?
Сколько? – три, каких? – восьмых – три восьмых,
Сколько? – семь, каких? – девятых – семь девятых,
Сколько? – две, каких? – шестых – две шестых,
Сколько? – пять, каких? – седьмых – пять седьмых.
У чисел, которые вверху и внизу дроби есть свое научное название: верхнее число называется числитель, а нижнее – знаменатель.
Постарайтесь запомнить это. Это важно! Числитель – наверху, знаменатель – внизу.
Знаменатель показывает на сколько частей мы разделили наше целое, а числитель показывает – сколько частей целого мы с вами взяли.
Чтобы лучше запомнить, где числитель, где знаменатель, есть простая напоминалочка:
«ЧЕЛОВЕК ХОДИТ ПО ЗЕМЛЕ».
Ч – числитель – «над», З – знаменатель «под».
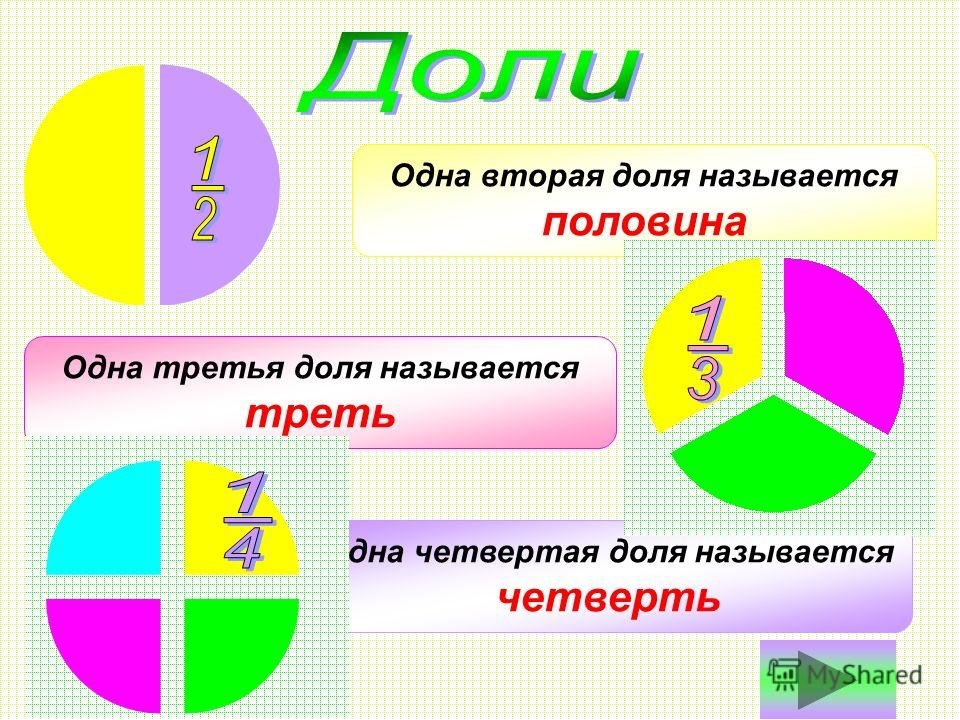
Есть одна разновидность дробей, которую в начальной школе выделяют в отдельную группу. Такие дроби называют долями. Если вам встретилось слово «доля», знайте, что это та же самая дробь, но только у нее числитель равен единице.
Мы постоянно сталкиваемся с ними в жизни.
Чаще всего мы встречаемся в жизни именно с половиной:
пол яблока — это одна вторая яблока, пол стакана – это одна вторая стакана.
Так же мы знакомы с одной третьей:
– это не что иное, как треть.
Треть грейфрута – это значит, разделили грейфрут на 3 части и взяли одну.
Точно так же мы с вами называем одну четвертую четвертью.
Например – школьная четверть. Мы с вами делим учебный год на 4 части и берем одну часть. Это и есть – четверть.
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 4.9 / 5. Количество оценок: 81
Доли. Обыкновенные дроби
Нам известно, что при подсчете чего-либо мы используем натуральные числа, но часто приходится что-то целое делить на части. Например, нам дан апельсин:
Допустим, нам надо разделить апельсин на 6 равных частей:
В этом случае каждую часть называют долей. То есть целый апельсин разделили на 6 частей, поэтому мы можем сказать, что апельсин это 1 целая, и 6 долей апельсина тоже составляет 1 целую:
Название долей зависит от числа частей. Каждая доля в нашем случае будет называться «одной шестой долей апельсина» или, короче, «одной шестой апельсина«. Если апельсин поделить на 8 частей, то мы получим восьмые доли. При этом, чем на большее число частей делят целое, тем меньше доля.
Например, рассмотрим брусок:
Разделим его на 5 частей:
То есть мы получим пятые доли бруска. Закрасим две части красным:
Теперь закрасим три части бруска:
Мы закрасили три пятые доли. Дробь, обозначающая эти доли, записывается так: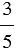 
.
Теперь закрасим желтым цветом пять частей бруска:
Мы закрасили пять пятых долей, то есть мы закрасили весь брусок. Дробь, обозначающая эти доли, записывается так: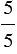 
.
Рассмотрим рисунок ниже:
Определения
Правильная дробь – это дробь, числитель которой меньше знаменателя.
Неправильная дробь – это дробь, у которой числитель больше знаменателя или равен ему.
Поделись с друзьями в социальных сетях:
Дробь. Правильные и неправильные дроби. Смешанные числа
Содержание
Дробь. Числитель и знаменатель дроби
Дробь записывают при помощи двух натуральных чисел, одно из которых стоит над горизонтальной чертой, а второе – под нею.
Знаменатель дроби показывает, на сколько одинаковых долей мы делим предмет или величину, а числитель дроби показывает, сколько таких долей взято.
Из рисунка 1 видно, что 24 километра составляют 4 из 7 частей маршрута. Таким образом, 1 часть маршрута равна
а весь маршрут равен
Термин дробь имеет синонимы: простая дробь, обыкновенная дробь, рациональная дробь, дробное число.
Правильные и неправильные дроби. Смешанные числа
– правильная дробь, 
и 
– неправильные дроби.
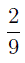
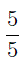
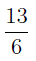
Неправильную дробь всегда можно представить в виде суммы целого числа и правильной дроби. Эту операцию называют выделением целой части из неправильной дроби и осуществляют при помощи деления с остатком числителя неправильной дроби на знаменатель.
Число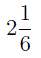 
является примером смешанного числа. Целое число 2 и правильную дробь 
называют целой и дробной частью смешанного числа соответственно.
Любое смешанное число всегда можно обратить в неправильную дробь, например,
Основное свойство дроби, сокращение дробей, несократимая дробь
Основным свойством дроби называют следующее
При помощи сокращений любую дробь можно превратить в равную ей несократимую дробь.
Дробь (математика)
| 8 | / 13 |  | числитель |
| числитель | знаменатель | знаменатель | |
| Две записи одной дроби | |||
Содержание
Виды дробей
Обыкновенные дроби
Обыкновенная (или простая) дробь — запись рационального числа в виде 
или 
где 
Горизонтальная или косая черта обозначает знак деления, в результате чего получается частное. Делимое называется числителем дроби, а делитель — знаменателем.
Обозначения обыкновенных дробей
Есть несколько видов записи обыкновенных дробей в печатном виде:
Правильные и неправильные дроби
Правильной называется дробь, у которой модуль числителя меньше модуля знаменателя. Дробь, не являющаяся правильной, называется неправильной, и представляет рациональное число, по модулю большее или равное единице.
Например, дроби 
, 
и 
— правильные дроби, в то время как 
, 
, 
и 
— неправильные дроби. Всякое целое число можно представить в виде неправильной обыкновенной дроби со знаменателем 1.
Смешанные дроби
Дробь, записанная в виде целого числа и правильной дроби, называется смешанной дробью и понимается как сумма этого числа и дроби. Любое рациональное число можно записать в виде смешанной дроби. В противоположность смешанной дроби, дробь, содержащая лишь числитель и знаменатель, называется простой.
Например, 
. В строгой математической литературе такую запись предпочитают не использовать из-за схожести обозначения смешанной дроби с обозначением произведения целого числа на дробь, а также из-за более громоздкой записи и менее удобных вычислений.
Высота дроби
Высота обыкновенной дроби — модуль суммы числителя и знаменателя этой дроби. Высота рационального числа — модуль суммы числителя и знаменателя несократимой обыкновенной дроби, соответствующей этому числу.
Например, высота дроби 
равна 
. Высота же соответствующего рационального числа равна 
, так как дробь сокращается на 
.
Составные дроби
Многоэтажной, или составной, дробью называется выражение, содержащее несколько горизонтальных (или реже — наклонных) черт:
или 
или 
Десятичные дроби
Десятичной дробью называют позиционную запись дроби. Она выглядит следующим образом:
Пример: 
.
Часть записи, которая стоит до позиционной запятой, является целой частью числа (дроби), а стоящая после запятой — дробной частью. Всякую обыкновенную дробь можно преобразовать в десятичную, которая в этом случае либо имеет конечное число знаков после запятой, либо является периодической дробью.
Вообще говоря, для позиционной записи числа́ можно использовать не только десятичную систему счисления, но и другие (в том числе и специфические, такие, как фибоначчиева).
Значение дроби и основное свойство дроби
Дробь является всего лишь записью числа. Одному и тому же числу могут соответствовать разные дроби, как обыкновенные, так и десятичные.
Если умножить числитель и знаменатель дроби на одинаковую величину:
то значение дроби останется прежним, хотя дроби — разные. Например:
И обратно, если числитель и знаменатель заданной дроби имеют общий делитель, то обе части можно разделить на него; такая операция называется сокращением дроби. Пример:
— здесь числитель и знаменатель дроби сократили на общий делитель 4.
Несократимой называется дробь, числитель и знаменатель которой взаимно просты, т. е. не имеют общих делителей, кроме 
Для десятичной дроби запись почти всегда однозначна, однако имеются исключения. Пример:
— две разные дроби соответствуют одному числу.
Действия над дробями
В этом разделе рассматриваются действия над обыкновенными дробями. О действиях над десятичными дробями см. Десятичная дробь.
Приведение к общему знаменателю
Для сравнения, сложения и вычитания дробей их следует преобразовать (привести) к виду с одним и тем же знаменателем. Пусть даны две дроби: 
и 
. Порядок действий:
После этого знаменатели обеих дробей совпадают (равны M). Вместо наименьшего общего кратного можно в простых случаях взять в качестве M любое другое общее кратное, например, произведение знаменателей. Пример см. ниже в разделе Сравнение.
Сравнение
Чтобы сравнить две обыкновенные дроби, следует привести их к общему знаменателю и сравнить числители получившихся дробей. Дробь с бо́льшим числителем будет больше.
Пример. Сравниваем 
и 
. НОК(4, 5) = 20. Приводим дроби к знаменателю 20.
Следовательно, 
Сложение и вычитание
Чтобы сложить две обыкновенные дроби, следует привести их к общему знаменателю. Затем сложить числители, а знаменатель оставить без изменений:
+ 
= 
+ 
= 
НОК знаменателей (здесь 2 и 3) равно 6. Приводим дробь к знаменателю 6, для этого числитель и знаменатель надо умножить на 3.
Получилось . Приводим дробь к тому же знаменателю, для этого числитель и знаменатель надо умножить на 2. Получилось .
Чтобы получить разность дробей, их также надо привести к общему знаменателю, а затем вычесть числители, знаменатель при этом оставить без изменений:
— 
= 
— =
НОК знаменателей (здесь 2 и 4) равно 4. Приводим дробь 
к знаменателю 4, для этого надо числитель и знаменатель умножить на 2. Получаем 
.
Умножение и деление
Чтобы умножить две обыкновенные дроби, нужно перемножить их числители и знаменатели:
В частности, чтобы умножить дробь на натуральное число, надо числитель умножить на число, а знаменатель оставить тем же:
В общем случае, числитель и знаменатель результирующей дроби могут не быть взаимно простыми, и может потребоваться сокращение дроби, например:
Чтобы поделить одну обыкновенную дробь на другую, нужно умножить первую на дробь, обратную второй:
Преобразование между разными форматами записи
Чтобы преобразовать обыкновенную дробь в дробь десятичную, следует разделить числитель на знаменатель. Результат может иметь конечное число десятичных знаков, но может быть и бесконечной периодической дробью. Примеры:
— бесконечно повторяющийся период принято записывать в круглых скобках.
Чтобы преобразовать десятичную дробь в дробь обыкновенную, следует представить её дробную часть в виде натурального числа, делённого на соответствующую степень 10. Затем к результату приписывается целая часть со знаком, формируя смешанную дробь. Пример:
История и этимология
Впервые в Европе данный термин употребил Леонардо Пизанский (1202). Поначалу европейские математики оперировали только с обыкновенными дробями, а в астрономии — с шестидесятеричными. Полноценная теория обыкновенных дробей и действий с ними сложилась в XVI веке (Тарталья, Клавиус).
В древней Руси дроби называли долями или ломаными числами. Термин дробь, как аналог латинского fractura, используется в «Арифметике» Магницкого (1703) как для обыкновенных, так и для десятичных дробей.
В Европе первые десятичные дроби ввёл Иммануил Бонфис около 1350 года, но широкое распространение они получили только после появления сочинения Симона Стевина «Десятая» (1585).
Обобщения
См. также
Литература
Примечания
Полезное
Смотреть что такое «Дробь (математика)» в других словарях:
Дробь — В Викисловаре есть статья «дробь» Наименование символа «⁄» (другое, распространённое по большей части в английском языке, название символа солидус (англ.), или слэш), например, в номерах домов. Так номер дома «5/17» читается «пять… … Википедия
Математика гармонии — Эта статья предлагается к удалению. Пояснение причин и соответствующее обсуждение вы можете найти на странице Википедия:К удалению/22 ноября 2012. Пока процесс обсуждени … Википедия
МАТЕМАТИКА — Математику обычно определяют, перечисляя названия некоторых из ее традиционных разделов. Прежде всего, это арифметика, которая занимается изучением чисел, отношений между ними и правил действий над числами. Факты арифметики допускают различные… … Энциклопедия Кольера
Периодическая дробь — Десятичная дробь дробь со знаменателем 10n, где n натуральное число. Имеет особую форму записи: целая часть в десятичной системе счисления, затем запятая и затем дробная часть в десятичной системе счисления, причём количество цифр дробной части … Википедия
Медианта (математика) — У этого термина существуют и другие значения, см. Медианта. Медиантой двух дробей и с положительными знаменателями называется дробь, числитель которой равен сумме числителей, а знаменатель сумме знаменателей, двух данных дробей:… … Википедия